Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 206
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
составляющие (рис.1). Значит, магнитная стрелка, вращающаяся на закреплённой вертикальной оси (компас), будет останавливаться в плоскости магнитного меридиана под действием именно горизонтальной составляющей магнитного поля Земли. Если с помощью кругового тока около стрелки создать ещё одно магнитное поле, то она установится по направлению равнодействующей напряженности обоих магнитных полей. Так как поле кругового тока нетрудно вычислить, зная величину тока, протекающего в витке, и радиус витка, то величину горизонтальной составляющей вектора напряжённости магнитного поля Земли 
можно определить по углу отклонения стрелки и величине силы тока.
H0 H
H1
Рис.1.
Определение горизонтальной составляющей напряженности магнитного поля Земли производится с помощью прибора, называемого тангенс-буссолью. Рассмотрим круговой проводник из n витков, прилегающих достаточно плотно друг к другу, расположенных вертикально в плоскости магнитного меридиана. В центре проводника поместим магнитную стрелку, вращающуюся вокруг вертикальной оси (при достаточно большом радиусе проводника можно считать, что магнитная стрелка находится в однородном магнитном поле). Если по виткам проводника пропустить ток, то возникает магнитное поле с напряженностью
, направленное перпендикулярно плоскости катушки. Таким образом, на стрелку будут действовать два взаимно перпендикулярных магнитных поля: магнитное поле Земли и поле тока.
На рис.2 изображено сечение катушки горизонтальной плоскостью. Здесь – вектор напряженности магнитного поля, созданного круговым током, - горизонтальная составляющая вектора напряженности магнитного поля Земли (рис.2 – вид сверху). Стрелка установится по направлению равнодействующей 
, т.е. по диагонали параллелограмма, сторонами которого будут вектора и .
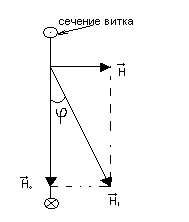
Рис.2.
Тогда получим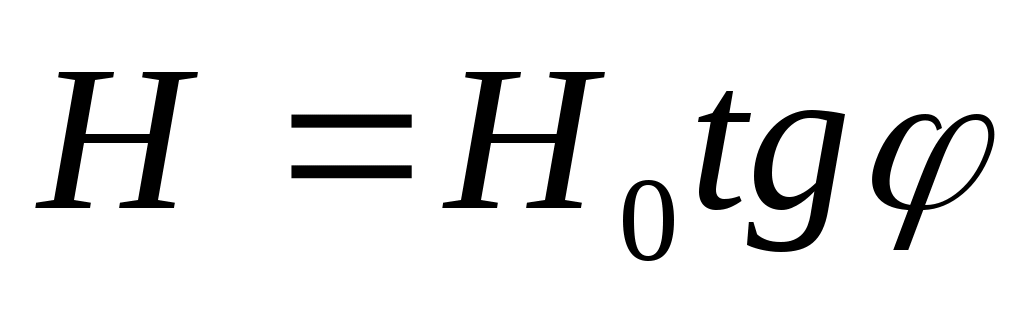
С другой стороны , напряженность магнитного поля в центре катушки тангенс-буссоли, исходя из закона Био-Савара-Лапласа, может быть определена по формуле:
Н = n I/ 2r,
где I – ток, r - радиус витков буссоли (r=25 см), n – число витков(n = 32). Тогда
nI / 2r = H0tg ;
H0 = n I. / 2r tg (1)
В общем случае тангенс-буссоль может быть ориентирована произвольно, тем более, что точная установка ее в направлении магнитного меридиана затруднительна. Тогда величину Н0 можно определить, переключая направление тока и записывая углы поворота стрелки компаса 1 и 2 от начального значения. Действительно, из рис.3 видно, что в этом случае
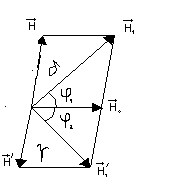
Рис.3.
1 + 2 + + =
Н /sin2=Н0 /sin ; H / sin1 = H0 /sin
Решением полученной системы является:
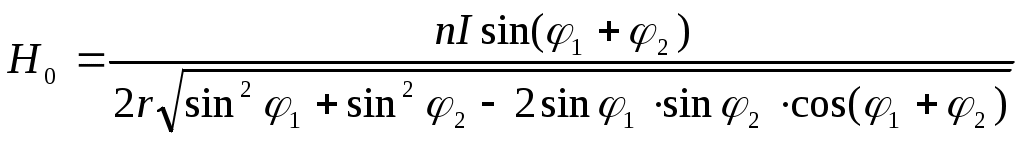
(2)
При 1 = 2 = эта формула превращается в формулу ( 1 ).
Электрическая схема установки изображена на рис. 4.
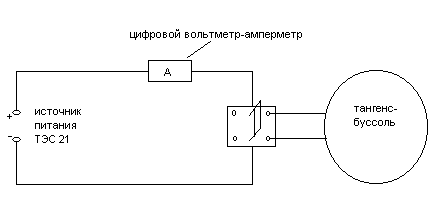
Рис. 4.
Порядок выполнения работы.
Упражнение 1.
1.Установить тангенс-буссоль в плоскости магнитного меридиана Земли (по магнитной стрелке).
2.Собрать схему и подключить установку к источнику питания. Замкнуть переключатель и установить с помощью источника питания такой ток, чтобы угол поворота магнитной стрелки был равным 450 . Записать значение силы тока по миллиамперметру I 1.
3.Переключателем изменить направление тока в буссоли и записать новое отклонение стрелки I 2 (перемена направления тока позволяет избавиться от ошибки, создаваемой неточным совпадением плоскости тангенс-буссоли с плоскостью магнитного меридиана). Повторить измерения несколько раз. Для расчета взять среднее арифметическое значение тока Icp. = (I1+I2)/2. Рассчитать Н0 по формуле (1).
4.Такие измерения произвести при 4-5 других значениях силы тока, так чтобы
= 300 , 350 , 400 , 500 , 55 0, 60 0
Данные занести в таблицу 1.
Таблица 1.
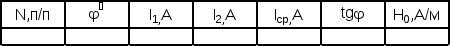
Упражнение 2.
Определение значения Н0 при произвольной ориентации тангенс-буссоли.
1.Сориентировать плоскость тангенс-буссоли так, чтобы угол между нормалью к плоскости и магнитной стрелкой был отличен от 0 и 900.
2.Нулевое значение угла компаса совместить с направлением Н0.
3.Пропустить по виткам тангенс-буссоли определённый ток.
4.Определить углы поворота стрелки компаса 1 и 2, переключая направление тока в буссоли.
5.Рассчитать значение Н0 по формуле (2).
Измерения повторить три раза. Данные занести в таблицу 2.
Таблица 2.
6.Сравнить значения Н
0, полученные в двух упражнениях.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1.Закон Био-Савара-Лапласа. Вектор индукции и напряженности магнитного поля. Как определяется направление dB?
2. Силовые линии магнитного поля. Поле кругового проводника с током. Вывести формулу для индукции магнитного поля в центре. Как направлен вектор В?
3. Метод определения горизонтальной составляющей напряженности магнитного поля Земли с помощью тангенс-буссоли.
4. Почему магнитная стрелка тангенс-буссоли должна быть малых размеров?
Литература:
1. Чечкин С.А. Основы геофизики,- Л., Гидрометеоиздат,1990;
Трофимова Т.И. Курс физики. -М., Высшая школа, 1997.
Элементы теории.
Отражение и преломление света на границе двух сред.
Пусть световой луч переходит из среды 1 с показателем преломления n1 в среду 2 с показателем преломления n2 . Падающий луч на границе двух диэлектриков разделяется на два: первый отражается от второй среды, а второй испытывает преломление в среду 2 (рис.1).
Рис.1.
Отражение и преломление света подчиняется следующим законам .
sin / sin = n12 (1) где n 12 = n 2 / n 1 - относительный показатель преломления, постоянная для данных сред величина, не зависящая от углов и .
Соотношение (1) носит название закона Снелиуса.
Если средой 1 является вакуум, то данное соотношение определяет абсолютный показатель преломления среды 2 :
sin / sin = n 2. (2)
Законы отражения и преломления будут справедливы, если среды 1 и 2 являются однородными и изотропными. Под однородной средой будем понимать такую среду, оптические свойства которой во всех её точках одинаковы, а под изотропной – среду, оптические свойства которой одинаковы по всем направлениям.
В случае, если луч распространяется в среде с большим показателем преломления (оптически более плотной) и преломляется в среду оптически менее плотную ( n2 < n 1 ), то sin > sin и, следовательно, угол > . По мере увеличения угла падения растёт и угол преломления. При падении света под некоторым определенным углом
можно определить по углу отклонения стрелки и величине силы тока. H0 H H1 Рис.1.
Определение горизонтальной составляющей напряженности магнитного поля Земли
производится с помощью прибора, называемого тангенс-буссолью. Рассмотрим круговой проводник из n витков, прилегающих достаточно плотно друг к другу, расположенных вертикально в плоскости магнитного меридиана. В центре проводника поместим магнитную стрелку, вращающуюся вокруг вертикальной оси (при достаточно большом радиусе проводника можно считать, что магнитная стрелка находится в однородном магнитном поле). Если по виткам проводника пропустить ток, то возникает магнитное поле с напряженностью
, направленное перпендикулярно плоскости катушки. Таким образом, на стрелку будут действовать два взаимно перпендикулярных магнитных поля: магнитное поле Земли и поле тока. На рис.2 изображено сечение катушки горизонтальной плоскостью. Здесь
– вектор напряженности магнитного поля, созданного круговым током, - горизонтальная составляющая вектора напряженности магнитного поля Земли (рис.2 – вид сверху). Стрелка установится по направлению равнодействующей , т.е. по диагонали параллелограмма, сторонами которого будут вектора и . Рис.2.
Тогда получим
С другой стороны , напряженность магнитного поля в центре катушки тангенс-буссоли, исходя из закона Био-Савара-Лапласа, может быть определена по формуле:
Н = n I/ 2r,
где I – ток, r - радиус витков буссоли (r=25 см), n – число витков(n = 32). Тогда
nI / 2r = H0tg ;
H0 = n I. / 2r tg (1)
В общем случае тангенс-буссоль может быть ориентирована произвольно, тем более, что точная установка ее в направлении магнитного меридиана затруднительна. Тогда величину Н0 можно определить, переключая направление тока и записывая углы поворота стрелки компаса 1 и 2 от начального значения. Действительно, из рис.3 видно, что в этом случае
Рис.3.
1 + 2 + + =
Н /sin2=Н0 /sin ; H / sin1 = H0 /sin
Решением полученной системы является:
(2)
При 1 = 2 = эта формула превращается в формулу ( 1 ).
Электрическая схема установки изображена на рис. 4.
Рис. 4.
Порядок выполнения работы.
Упражнение 1.
1.Установить тангенс-буссоль в плоскости магнитного меридиана Земли (по магнитной стрелке).
2.Собрать схему и подключить установку к источнику питания. Замкнуть переключатель и установить с помощью источника питания такой ток, чтобы угол поворота магнитной стрелки был равным 450 . Записать значение силы тока по миллиамперметру I 1.
3.Переключателем изменить направление тока в буссоли и записать новое отклонение стрелки I 2 (перемена направления тока позволяет избавиться от ошибки, создаваемой неточным совпадением плоскости тангенс-буссоли с плоскостью магнитного меридиана). Повторить измерения несколько раз. Для расчета взять среднее арифметическое значение тока Icp. = (I1+I2)/2. Рассчитать Н0 по формуле (1).
4.Такие измерения произвести при 4-5 других значениях силы тока, так чтобы
= 300 , 350 , 400 , 500 , 55 0, 60 0
Данные занести в таблицу 1.
Таблица 1.
Упражнение 2.
Определение значения Н0 при произвольной ориентации тангенс-буссоли.
1.Сориентировать плоскость тангенс-буссоли так, чтобы угол между нормалью к плоскости и магнитной стрелкой был отличен от 0 и 900.
2.Нулевое значение угла компаса совместить с направлением Н0.
3.Пропустить по виткам тангенс-буссоли определённый ток.
4.Определить углы поворота стрелки компаса 1 и 2, переключая направление тока в буссоли.
5.Рассчитать значение Н0 по формуле (2).
Измерения повторить три раза. Данные занести в таблицу 2.
Таблица 2.
6.Сравнить значения Н
0, полученные в двух упражнениях.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1.Закон Био-Савара-Лапласа. Вектор индукции и напряженности магнитного поля. Как определяется направление dB?
2. Силовые линии магнитного поля. Поле кругового проводника с током. Вывести формулу для индукции магнитного поля в центре. Как направлен вектор В?
3. Метод определения горизонтальной составляющей напряженности магнитного поля Земли с помощью тангенс-буссоли.
4. Почему магнитная стрелка тангенс-буссоли должна быть малых размеров?
Литература:
1. Чечкин С.А. Основы геофизики,- Л., Гидрометеоиздат,1990;
-
Дж. Д. Макдугалл. Краткая история планеты Земля, Санкт-Петербург, 2001;
Трофимова Т.И. Курс физики. -М., Высшая школа, 1997.
Лабораторная работа № 9.
Изучение методов измерения оптических
показателей преломления твердых тел.
Элементы теории.
Отражение и преломление света на границе двух сред.
Пусть световой луч переходит из среды 1 с показателем преломления n1 в среду 2 с показателем преломления n2 . Падающий луч на границе двух диэлектриков разделяется на два: первый отражается от второй среды, а второй испытывает преломление в среду 2 (рис.1).
-
n
1 -
n2
Рис.1.
Отражение и преломление света подчиняется следующим законам .
-
Луч падающий, нормаль к поверхности и луч отраженный лежат в одной плоскости, причем угол падения равен углу отражения . -
Луч падающий, луч преломленный и нормаль к границе раздела двух сред лежат в одной плоскости, а угол падения и угол преломления для данных двух сред связаны соотношением
sin / sin = n12 (1) где n 12 = n 2 / n 1 - относительный показатель преломления, постоянная для данных сред величина, не зависящая от углов и .
Соотношение (1) носит название закона Снелиуса.
Если средой 1 является вакуум, то данное соотношение определяет абсолютный показатель преломления среды 2 :
sin / sin = n 2. (2)
Законы отражения и преломления будут справедливы, если среды 1 и 2 являются однородными и изотропными. Под однородной средой будем понимать такую среду, оптические свойства которой во всех её точках одинаковы, а под изотропной – среду, оптические свойства которой одинаковы по всем направлениям.
В случае, если луч распространяется в среде с большим показателем преломления (оптически более плотной) и преломляется в среду оптически менее плотную ( n2 < n 1 ), то sin > sin и, следовательно, угол > . По мере увеличения угла падения растёт и угол преломления. При падении света под некоторым определенным углом