а — в — различные конфигурации пазов двухклеточных роторов

использована или воздушный зазор взят слишком большим. В обоих случаях в расчет должны быть внесены соответствующие коррективы.

При дальнейшем расчете магнитной цепи определяют магнит­ные напряжения ярм статора и ротора.
9.9.4. Магнитное напряжение ярм статора и ротора.

Намагничивающий ток

---

Магнитное напряжение ярма статора, А,
F_a = L_a H_a, (9.116)
где L_a — длина средней магнитной силовой линии в ярме статора, м; Н_а — напряженность поля при индукции В_а по кривой намагничива­ния для ярма, принятой при проектировании стали, А/м.

Индукция в ярме статора, Тл,
В_а = Ф / (2h'_al_ст1 k_c1 ), (9.117)
где h'_а — расчетная высота ярма статора, м:
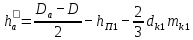(9.118)
где d_k1 и m_k1 — диаметр и число рядов аксиальных вентиляционных каналов в сердечнике статора; при отсутствии каналов m_k1 = 0.

Длина средней магнитной силовой линии в ярме статора, м,
L_a = (D_a - h_a) / (2p), (9.119)
где h_a — высота ярма статора, м:
h_a = (D_a - D) / 2 – h_п1. (9.120)
Магнитное напряжение ярма ротора, А,
F_j = L_j H_j (9.121)
где H_j — напряженность поля в ярме при индукции B_j по кривой намагничивания для ярма принятой при проектировании стали. Индукция в ярме ротора, Тл,
В_j = Ф / (2 h'_j l_ст2 k_c2 ), (9.122)
где k_с2 — коэффициент заполнения сталью ярма ротора (по табл. 9.13); h'_j — расчетная высота ярма ротора, м.

Для роторов с посадкой сердечника на втулку или на оребрен­ный вал (крупные асинхронные двигатели) расчетная высота ярма статора (см. рис. 9.43), м,
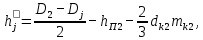(9.123)
В двигателях с непосредственной посадкой сердечника ротора на вал внутренний диаметр ротора равен диаметру вала: D_j = D_B. B таких двигателях с 2р = 2 или 4 учитывают, что часть магнитных силовых линий потока замыкается через вал. Поэтому в двигателях с 2р = 2 расчетную высоту ярма ротора, м, определяют из выра­жения
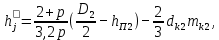. (9.124)
и длина силовых линий в ярме, м,
L_j = 2 h_j, (9.125)
где высота ярма ротора, м,
h_j = (D₂ - D_в) / 2 - h_п2. (9.126)
В двигателях с 2р = 4 с непосредственной посадкой сердечника ротора на вал, имеющих размерные соотношения, при которых

---

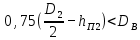, расчетную высоту ярма ротора определяют по (9.124), при других размерных соотношениях — по (9.126).

Длина средней магнитной силовой линии в ярме ротора всех двигателей, кроме двухполюсных, с непосредственной посадкой сер­дечника ротора на вал, м,

L_j = π(D_j + h_j) / (2p), (9.127)
где
h_j = (D₂ — D_j) / 2 — h_пa.
На этом расчет магнитных напряжений участков магнитной цепи двигателя заканчивается. Суммарное магнитное напряжение магнитной цепи (на пару полюсов), А,
F_u = F_δ + F_z1 + F_z2 + F_a + F_j. (9.128)
Коэффициент насыщения магнитной цепи
k_μ = F_u/ F_δ. (9.129)
Намагничивающий ток, А,
I_μ ≈ 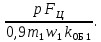(9.130)
Намагничивающий ток выражается также в процентах или в до­лях номинального тока двигателя:
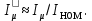(9.131)
Относительное значение I^*_μ служит определенным критерием правильности произведенного выбора и расчета размеров и обмот­ки двигателя. Так, если при проектировании четырехполюсного двигателя средней мощности расчет показал, что I^*_μ < 0,20.. .0,18, то в большинстве случаев это свидетельствует о том, что размеры машины выбраны завышенными и активные материалы недоиспользо­ваны. Такой двигатель может иметь высокие КПД и cosφ, но плохие показатели расхода материалов на единицу мощности, большие массу и габариты.

Если же в аналогичном двигателе I^*_μ > 0,3...0,4, то это в большин­стве случаев означает, что либо его габариты взяты меньшими, чем следовало, либо неправильно выбраны размерные соотношения участков магнитопровода. Двигатель будет иметь низкие КПД и cosφ.

В небольших двигателях мощностью менее 2...3 кВт I^*_μ может до­стигать значения 0,5...0,6, несмотря на правильно выбранные разме­ры и малое насыщение магнитопровода. Это объясняется относите­льно большим значением магнитного напряжения воздушного зазора, характерным для двигателей малой мощности [6].
9.10. ПАРАМЕТРЫ АСИНХРОННОЙ МАШИНЫ

ДЛЯ НОМИНАЛЬНОГО РЕЖИМА
Параметрами асинхронной машины называют активные и ин­дуктивные сопротивления обмоток статора r₁, x₁, ротора r₂, х₂

---

или приведенные к числу витков обмотки статора сопротивления рото­ра r'₂ и х'₂, сопротивление взаимной индуктивности х₁₂ и расчетное сопротивление r₁₂ (или r_μ), введением которого учитывают влияние потерь в стали статора на характеристики двигателя.

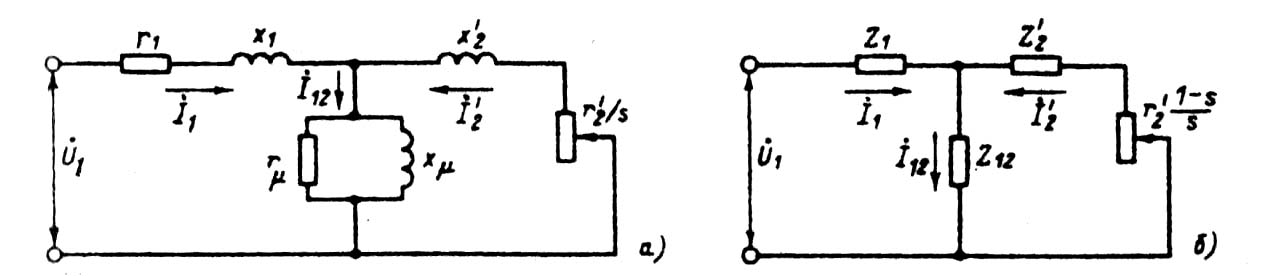
Рис. 9.47. Схемы замещения фазы обмотки приведенной асинхронной машины
Известные из общей теории электрических машин схемы заме­щения фазы асинхронной машины, основанные на приведении про­цессов во вращающейся машине к неподвижной, приведены на рис. 9.47. Физические процессы в асинхронной машине наглядно отражает схема, изображенная на рис. 9.47, а. Но для расчета оказалось удобнее преобразовать ее в схему, показанную на рис. 9.47, б.

Параметры схемы замещения не остаются неизменными при различных режимах работы машины. С увеличением нагрузки увеличивается поток рассеяния, и в связи с этим из-за возрастания насыщения отдельных участков магнитопровода полями рассеяния уменьшаются индуктивные сопротивления х₁ и х₂.

Увеличение скольжения в двигателях с короткозамкнутым рото­ром приводит к возрастанию действия эффекта вытеснения тока, что вызывает изменение сопротивлений обмотки ротора r₂ и х₂. При расчете рабочих режимов машины в пределах изменения скольже­ния от холостого хода до номинального эти изменения незначитель­ны и ими обычно пренебрегают.

При расчете пусковых режимов, в которых токи машины в не­сколько раз превышают номинальный, а частота тока в роторе близка к частоте питающей сети, в большинстве случаев приходится учитывать изменение параметров от насыщения участков магнитопровода кода полями рассеяния и от влияния эффекта вытеснения тока.

9.10.1. Активные сопротивления обмоток статора и фазного ротора
Активные сопротивления r и r₂, Ом, определяют по основной расчетной формуле (5.1):
r = k_Rρ_υ 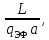(9.132)
где L — общая длина эффективных проводников фазы обмотки, м; q_эФ — площадь поперечного сечения эффективного проводника, м :

---

q_эф = q_элn_эл; (9.133)
q_эл — площадь поперечного сечения элементарного проводника; n_эл — число элементарных проводников в одном эффективном; а — число параллельных ветвей обмотки; ρ_υ — удельное сопротивление материала обмотки при расчетной температуре, Ом•м; k_R — коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока.

В проводниках обмотки статора асинхронных машин эффект вытеснения тока проявляется незначительно из-за малых размеров элементарных проводников. Поэтому в расчетах нормальных ма­шин, как правило, принимают k_R = 1 . Некоторое увеличение потерь,

обусловленное действием эффекта вытеснения тока, относят к дополнительным потерям.

В обмотках фазных роторов k_R также принимают равным едини­це независимо от размеров и числа проводников в пазу, так как час­тота тока в них при номинальном и близких к нему режимах очень мала.

Общая длина проводников фазы обмотки L, м,
L = l_cp w, (9.134)
гдеl_cp — средняя длина витка обмотки, м; w — число витков фазы. Среднюю длину витка l_ср находят как сумму прямолинейных па­зовых и изогнутых лобовых частей катушки:
l_ср = 2 (l_п + l_л). (9.135)
Длина пазовой части l_п равна конструктивной длине сердечни­ков машины:
l_п = l_1(2).
Лобовая часть катушки имеет сложную конфигурацию (рис. 9.48). Точные расчеты ее длины и длины вылета лобовой части тре­буют предварительного определения всех размеров катушки и со­пряжены со значительными объемами расчетов, данные которых в дальнейшем электромагнитном расчете обычно не используются. Для машин малой и средней мощности и в большинстве случаев для крупных машин достаточно точные для практических расче­тов результаты дают эмпирические формулы, учитывающие основные особенности конструктивных форм катушек.

Катушки всыпной обмотки ста­тора. Длина лобовой части, м,
l_л = K_лb_кт + 2В; (9.136)
вылет лобовых частей обмотки, м,
l_выл = K_лb_кт+ В. (9.137)


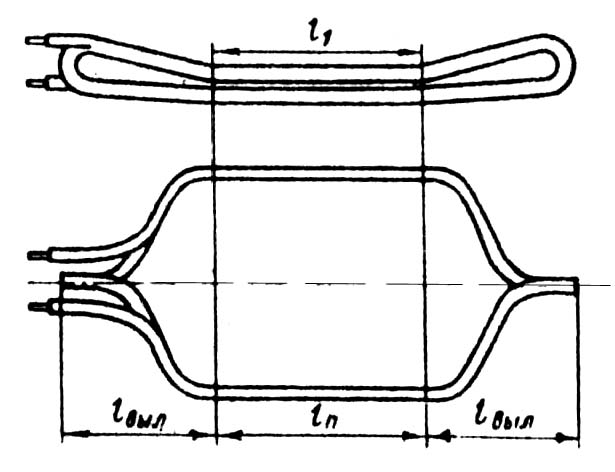
Рис. 9.48. Катушка двухслойной об­мотки статора
В этих формулах b_кт — средняя ширина катушки, м, определяемая по окружности, проходящей по серединам высоты пазов:

---

Смотрите также файлы

• Контрольная работа по дисциплине Мировая экономика Вариант 3 Магнитогорск 2021 г. Проблемы интеграции в мировой торговле.docx

• Кратко расскажите о революции в России 1917 г., ее причинах и последствиях.docx

• Аутизм. Особенности работы с детьми с расстройством аутистического спектра. Видео Мир глазами аутиста.pdf

• Первая помощь содержание, объем, организационные и юридические основы, общие принципы оказания.doc

• Результат попытки теста.docx