Коэффициент магнитной проводимости лобового рассеяния
λ_л = 0,34 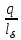(l_л – 0,64 β τ ) (9.159)
где q и l_л — число пазов на полюс и фазу и длина лобовой части витка обмотки; β = у_расч / τ — укорочение шага обмотки, для которой прово­дится расчет, т. е. обмотки статора или фазного ротора.

Коэффициент магнитной проводимости дифференциального рассеяния для обмоток статора и фазного ротора
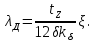(9.160)
Значение коэффициента ξ зависит от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора.

Ниже приводятся формулы, в которые при расчете ξ, для обмо­ток статора или ротора следует подставлять данные обмоток и зубцовых зон соответственно статора или ротора.

Для обмоток статора и ротора при q, выраженном целым чис­лом (q ≥ 2), для обмотки с β = 1
ξ = 2 + 0,022 q² – k²_об(1 + Δz); (9.161)
при укороченном шаге обмотки (β < 1)
ξ = k''q² + k'_β – k²_об(1 + Δz); (9.162)
при дробном (q ≥ 2)
ξ = k''q² + 2k''_β – k²_об( 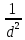+ Δz); (9.163)
при дробном q, значение которого 1 < q < 2,
ξ = k''q² + 2k''_β – 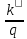– k²_об( 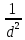+ Δz); (9.164)
В этих формулах коэффициенты Δz, k', k" и k"_β определяют по кривым, приведенным на рис. 9.51. Для определения k"_β и k' необ­ходимо найти дробную часть числа q, равную c/d (дробное число q = b + c/d, где b — целое число, c/d < 1 — дробная часть числа q), коэффициент k'_β — по (9.156) или (9.157).

Индуктивное сопротивление обмотки фазного ротора, опреде­ленное по (9.152), должно быть приведено к числу витков обмотки статора:
х'₂ = v₁₂x₂, (9.165)
где v₁₂ — коэффициент приведения сопротивлений по (9.151).

9.10.3. Сопротивления обмоток двигателей с короткозамкнутыми роторами
Активное сопротивление фазы обмотки статора двигателя с короткозамкнутым ротором рассчитывается так же, как и для двигате­ля с фазным ротором.

---

Активное сопротивление фазы короткозамкнутого ротора опреде­ляется следующим образом. Как говорилось выше, за фазу обмотки, выполненной в виде беличьей клетки, принимают один стержень и два участка замыкающих колец (см. рис. 9,35). Токи в стержнях и за­мыкающих кольцах различны, поэтому их сопротивления при рас­чете общего сопротивления фазы должны быть приведены к одному току. Таким образом, сопротивление фазы короткозамкнутого ро­тора r₂ является расчетным параметром, полученным из условия равенства электрических




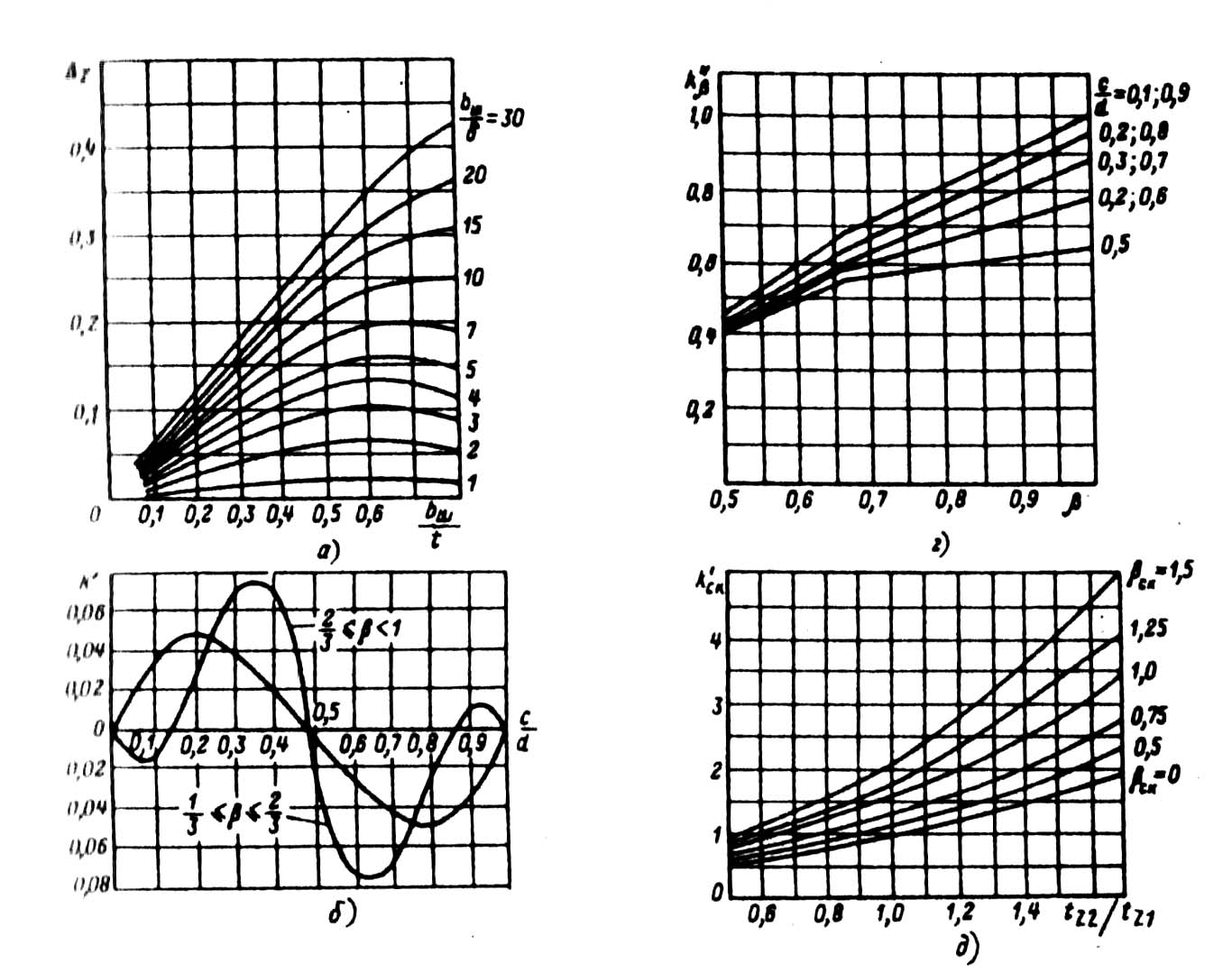
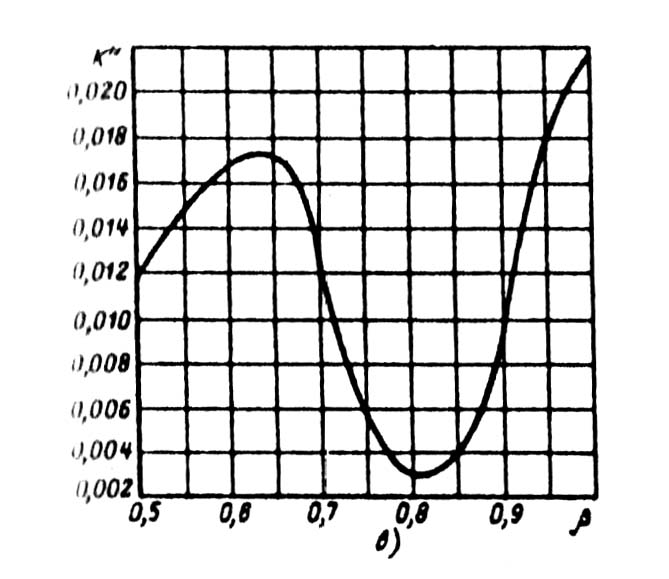
Рис. 9.51. Коэффициенты к расчету проводимости

дифференциального рассеяния:
а — коэффициент Δz в зависимости от размерных соотношений b_ш/t_z и b_ш/S;

б — коэффициент k' в зависимости от дробной части числа q;

в — коэф­фициент К' в зависимости от укорочения шага обмотки β;

г — коэффициент К''_β в зависимости от укорочения шага обмотки β и дробной части чис­ла q;

д — коэффициент k'_ск в зависимости от соот­ношения t_z2/t_z1 и относительного скоса пазов β_ck

потерь в сопротивлении r₂ от тока I₂ и сум­марных потерь в стержне и участках замыкающих колец соответственно от тока в стержне I_c и тока в замыкающем кольце I_кл реальной машины:
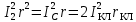(9.166)
где I_с — ток в стержне ротора; I_кл — ток в замыкающих кольцах; r_C — сопротивление стержня; r_кл — сопротивление участка замыка­ющего кольца, заключенного между двумя соседними стержнями (см. рис. 9.35).

Ток I_с называют током ротора и в расчетах обозначают I₂.

Учитывая, что
I_кл = I_с/Δ = I₂ /Δ, (9.167)
где Δ = 2sin 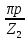— (см. § 9.7), из (9.167), получаем

r₂ = r_с + 2 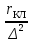(9.168)
где

r_c = 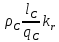; (9.169)

r_кл = 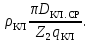(9.170)
В этих выражениях I_с — полная длина стержня, равная расстоя­нию между замыкающими кольцами, м; D_кл._ср — средний диаметр замыкающих колец, м (см. рис. 9.37):

---

D_кл._ср = D₂ - h_кл; (9.171)
q_c — сечение стержня, м²; k_r — коэффициент увеличения активного со­противления стержня от действия эффекта вытеснения тока; при рас­чете рабочих режимов в пределах изменения скольжения от холостого хода до номинального для всех роторов принимают k_r = 1; q_кл — площадь поперечного сечения замыкающего кольца, м²; р_с и р_кл — соответственно удельные сопротивления материала стержня и замыкающих колец, Ом м, при расчетной температуре (см. табл. 5.1).

Сопротивление r₂ для дальнейших расчетов должно быть приве­дено к числу витков первичной обмотки. Выражение коэффициента приведения для сопротивления фазы короткозамкнутого ротора по­лучают, подставляя в (9.151) значения m₂ = Z₂, w₂ = 1/2, k_об2 = 1 и учитывая влияние скоса пазов:
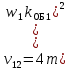(9.172)
где коэффициент скоса пазов (по 3.17)
k_ск = 2 sin ;
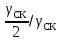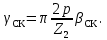
Обычно значения β_ск выражают в долях зубцового деления ротора t_z2. При скосе пазов ротора на одно зубцовое деление стато­ра γ_ck = π2p / Z₁. В этом случае в двигателях с 2р = 2 из-за малости угла γ_ck принимают k_cк = 1.

Приведенное значение активного сопротивления фазы обмотки короткозамкнутого ротора
r'₂ = r₂ v₁₂. (9.173)
Индуктивное сопротивление рассеяния обмотки статора асинх­ронного двигателя с короткозамкнутым ротором рассчитывается по той же формуле, что и для статора с фазными роторами, т. е.
x = 1,58 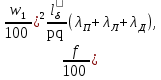(9.174)
Входящий в формулу коэффициент магнитной проводимости пазового рассеяния λ_п определяют в зависимости от конфигурации пазов по формулам табл. 9.26.

Коэффициент магнитной проводимости лобового рассеяния λ_л определяется по (9.159).

Коэффициент магнитной проводимости дифференциального рассеяния λ_д1 определяют по формуле

---

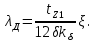(9.174а)
в которой ξ, находят следующим образом.

При открытых пазах статора и отсутствии скоса статора или ротора
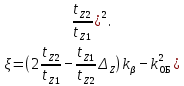(9.175)
При полузакрытых или полуоткрытых пазах статора с учетом скоса пазов
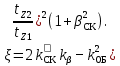(9.176)
В этих формулах t_z1 и t_z2 — зубцовые деления статора и ротора; Δ_Z определяют по кривой рис. 9.51, a, k_β определяют по (9.155) или (9.158); β_cк = β_cк/t_z2 — скос пазов, выраженный в долях зубцового деления ротора. При отсутствии скоса пазов b_ск = 0; k'_cк определяют по кривым рис. 9.51, д в зависимости от t_z2/t_z1 и β_cк (при отсутствии скоса пазов — по кривой, соответствующей β_ск = 0).

Индуктивное сопротивление обмотки короткозамкнутого ротора определяют по формуле
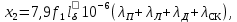(9.177)
полученной после подстановки в (9.152) значений m₂ = Z₂ и q₂ = 1/(2р) обмотки короткозамкнутого ротора и введения дополнительного слагаемого λ_ск.

Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора рассчитывают по приведенным в табл. 9.27 формулам в зависимости от конфигурации паза ротора (рис. 9.52).
Таблица 9.27. Расчетные формулы для определения коэффициентов

магнитной проводимости пазового рассеяния короткозамкнутых роторов

Рисунок	Расчетные формулы
9.52, а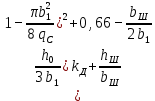
9.52,6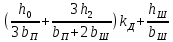
9.52, в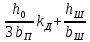
9.52, г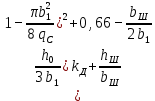
9.52, д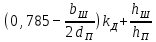

---

При расчете номинального режима двигателя во всех формулах k_д= 1.

При закрытых пазах ротора любой конфигурации (рис. 9.52, а—д) в расчетных формулах табл. 9.27 нужно при шлицах по рис. 9.52, е слагаемые h_ш /b_ш заменить на 0,3 + 1,12 • 10⁶ 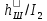, по рис. 9.52, ж — на h_ш/b_ш + 1,12 • 10⁶ 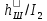, где 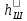— толщина ферромагнит­ной перемычки над пазом, м; I₂ — ток ротора, А.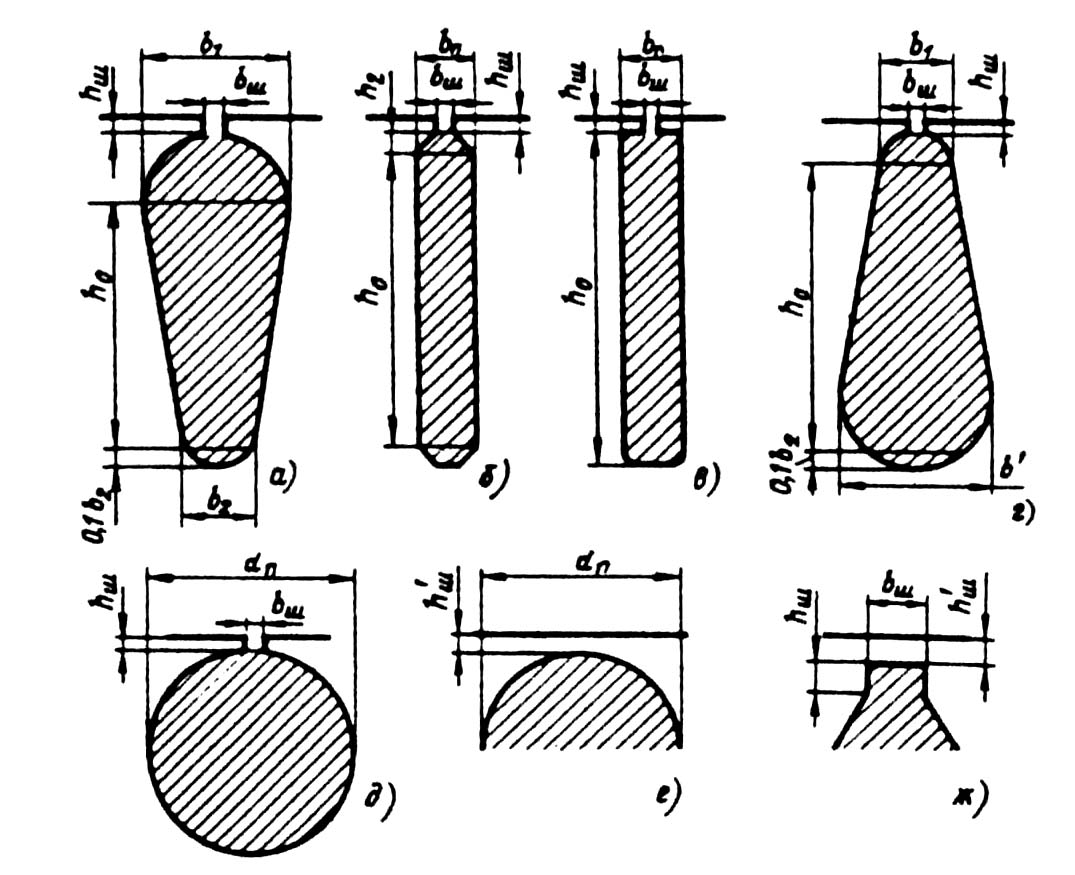


Рис. 9.52. К расчету коэффициентов магнитной проводимости

пазового рассеяния короткозамкнутых роторов:

а — д — полузакрытые пазы; е, ж — закрытые пазы
Коэффициент магнитной проводимости лобового рассеяния рассчитывают в зависимости от размеров и расположения замыкающих колец обмотки по следующим формулам.

В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 9.37, б), используют формулу

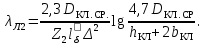
(9.178)
Если замыкающие кольца отставлены от торцов ротора (см. рис. 9.37, а), как, например, в обмотке, выполненной из медных или латунных стержней, впаянных в замыкающие кольца, расчет прово­дят по формуле

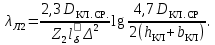(9.179)
В этих формулах D_кл.ср — средний диаметр замыкающих колец по (9.171); Δ = 2 sin πρ/Z₂ — коэффициент приведения токов в кольце к току в стержне; h_кл и b_кл — средние высота и ширина колец (см. рис. 9.37); 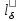; — по (9.154).

Коэффициент магнитной проводимости дифференциального рассеяния обмотки, короткозамкнутого ротора

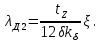(9.180)

где

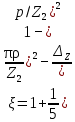(9.181)
Δ_Z находят по кривым рис. 9.51, а.

Как видно из (9.181), при большом числе пазов ротора, приходя­щихся на пару полюсов: Z

---

Смотрите также файлы

• Контрольная работа по дисциплине Мировая экономика Вариант 3 Магнитогорск 2021 г. Проблемы интеграции в мировой торговле.docx

• Кратко расскажите о революции в России 1917 г., ее причинах и последствиях.docx

• Аутизм. Особенности работы с детьми с расстройством аутистического спектра. Видео Мир глазами аутиста.pdf

• Первая помощь содержание, объем, организационные и юридические основы, общие принципы оказания.doc

• Результат попытки теста.docx