ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 390
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
r = hc /hr = 1 + φ. (9.250)
Для круглых стержней (рис. 9.59, б)
kr = qс / qr = 1 + φ. (9.251)
Функция φкр для круглого стержня представлена на рис. 9.57.
Для грушевидных стержней (рис. 9.59, в)
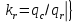(9.252)
Площадь сечения qr при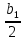
≤ hr ≤ h1 +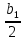
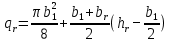, (9.253)
где
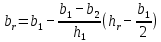
hr = hc / (l + φ).
При hr ≤ b1/2 площадь
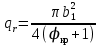(9.254)
При hr > h1 + b1/2 принимают qr ≈ qc и kr = 1. Для трапецеидальных стержней с узкой верхней частью (см. рис. 9.59, г)
kr = qc /qr,
qс определяют по (9.252). Площадь qr при hr ≤ b1/2 определяют по (9.254) и при hr ≥ b1/2 — по (9.253), причем
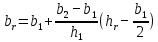(9.255)
Для других конфигураций стержней kr, может быть определен из общего выражения kr = qc /qr с учетом размерных соотношений стержня и глубины проникновения тока в стержень hr.
Для расчета характеристик необходимо учитывать изменение сопротивления всей обмотки ротора r2 поэтому удобно ввести коэффициент общего увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока:
KR = r2ξ/r2, (9.256)
гдеr2ξ — сопротивление фазы короткозамкнутого ротора с учетом влияния эффекта вытеснения тока.
Выражение (9.256) легко преобразовать в более удобный для расчета вид:
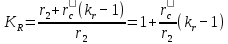(9.257)
Для прямоугольных стержней это выражение приобретает вид
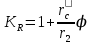. (9.258)
В (9.257) и (9.258) для роторов без радиальных вентиляционных каналов с литой обмоткой (с прилегающими замыкающими кольцами) r'с = rс.
Для роторов с радиальными вентиляционными каналами и роторов с отставленными замыкающими кольцами
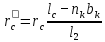
(9.259)
где lс — полная длина стержня, равная расстоянию между замыкающими кольцами, м; nк и bk — число и ширина, м, радиальных вентиляционных каналов; l2 — длина сердечника ротора, м.
Активное сопротивление фазы обмотки ротора с учетом вытеснения тока будет равно:
r2ξ = r2KR. (9.260)
Обозначив коэффициентом Кх изменение индуктивного сопротивления фазы обмотки ротора от действия эффекта вытеснения тока, получим
x2ξ = x2Kx, (9.261)
тогда
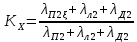(9.262)
где λп2ξ — коэффициент магнитной проводимости пазового рассеяния с учетом эффекта вытеснения тока:
λп2ξ = λп2 - Δ λп2ξ
здесь
Δ λп2ξ = λ'п2 (1 – kД);
λ'п2 — коэффициент магнитной проводимости участка паза, занятого проводником с обмоткой (выражение для определения λ'п2 в формулах табл. 9.27 является множителем перед коэффициентом kд).
Влияние насыщения на параметры. В предыдущих параграфах рассматривались методы расчета параметров при допущении отсутствия насыщения стали магнитопровода полями рассеяния, магнитная проницаемость которой принималась равной бесконечности. При расчетах параметров холостого хода и рабочих режимов это допущение вполне оправдано, так как токи в этих режимах относительно малы и потоки рассеяния не создают заметного падения магнитного напряжения в стали зубцов. При увеличении скольжения свыше критического и в пусковых режимах токи в обмотках возрастают и потоки рассеяния увеличиваются. Коронки зубцов статора и ротора в машинах средней и большой мощности в большинстве случаев оказываются сильно насыщенными.
Насыщение коронок зубцов (рис. 9.60) приводит к увеличению магнитного сопротивления для части потока рассеяния, магнитные линии которого замыкаются через верхнюю часть паза. Поэтому коэффициент магнитной проводимости пазового рассеяния уменьшается. Несколько снижается также магнитная проводимость дифференциального рассеяния. На коэффициент магнитной проводимости лобового рассеяния насыщение стали потоками рассеяния влияния не оказывает.
Уменьшение потока пазового рассеяния из-за насыщения приближенно учитывают введением дополнительного раскрытия паза
, равного сэ. Дополнительное раскрытие сэ принимается таким, чтобы его магнитное сопротивление потоку рассеяния было равно магнитному сопротивлению насыщенных участков зубцов. При этом условии можно использовать для расчета коэффициент магнитной проводимости паза с учетом насыщения обычные формулы, предполагая, что μст = ∞. Уменьшение λп из-за насыщения участков зубцов
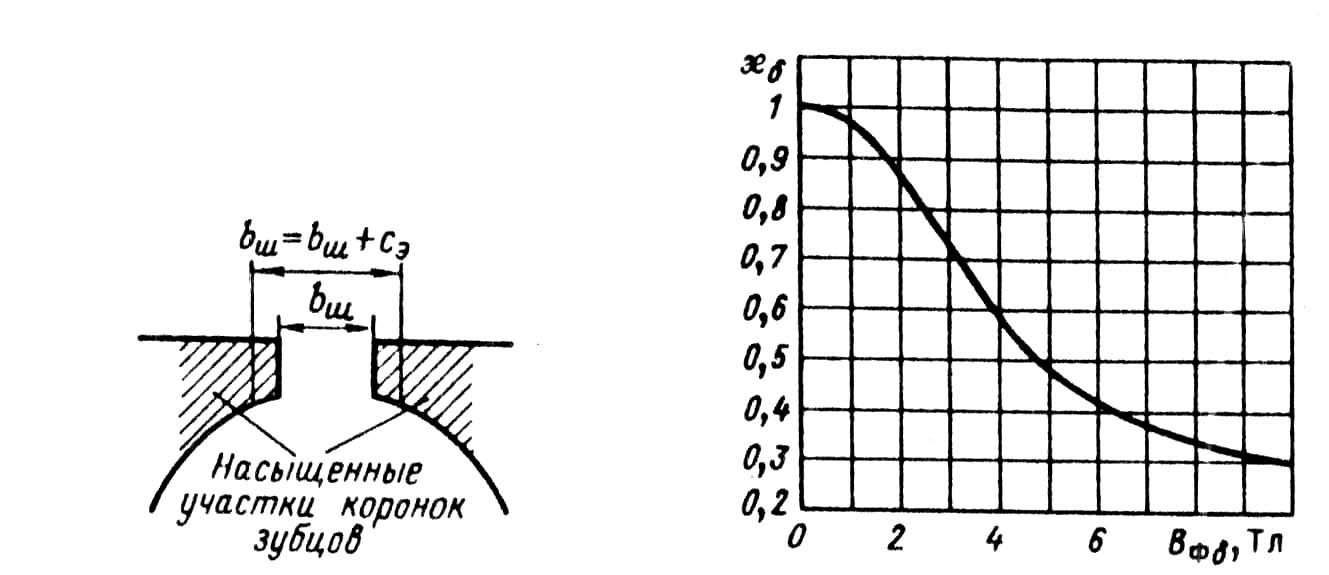
Рис. 9.60. Насыщение участков коронок Рис. 9.61. Функция Ks в зависимости
зубцов потоком рассеяния от фиктивной индукции Bδф
(Δλп.нас) будет определяться сэ. Таким образом, сэ зависит от уровня насыщения верхней части зубцов потоками рассеяния и, следовательно, от МДС паза, т. е. от тока в обмотке. Так как ток обмотки, в свою очередь, зависит от индуктивного сопротивления, определяемого магнитной проводимостью, то расчет приходится проводить методом последовательных приближений. Первоначально задаются предполагаемой кратностью увеличения тока, обусловленной уменьшением индуктивного сопротивления из-за насыщения зубцовой зоны:
kнас = Iнас / I,
где I — ток, рассчитанный для данного режима без учета насыщения; Iнас — ток в этом же режиме работы машины при насыщении участков зубцов полями рассеяния.
Ориентировочно для расчета пусковых режимов принимают kнас = 1,25...1,4; для режима максимального момента kнас = 1,1...1,2.
Для двигателей с открытыми пазами следует задаваться меньшими значениями kнас, при полузакрытых пазах — большими.
Расчет проводят в следующей последовательности. Определяют среднюю МДС обмотки, отнесенную к одному пазу обмотки статора:
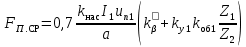(9.263)
где I1 — ток статора, соответствующий расчетному режиму, без учета насыщения; а — число параллельных ветвей обмотки статора; uп1— число эффективных проводников в пазу статора;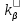
— коэффициент, учитывающий уменьшение МДС паза, вызванное укорочением шага обмотки, рассчитывается по (9.156) или по (9.157); ky1 — коэффициент укорочения шага обмотки.
По средней МДС F
п.cp рассчитывают фиктивную индукцию потока рассеяния в воздушном зазоре, Тл:
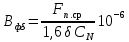(9.264)
где коэффициент
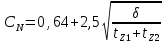(9.265)
(tZ1 и tZ2 — зубцовые деления статора и ротора).
По полученному значению Bδф определяют отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом kδ, значение которого находят по кривой рис. 9.61.
Далее рассчитывают значения дополнительного эквивалентного раскрытия пазов статора и ротора (сЭ1 и сЭ2), магнитные напряжения которых будут эквивалентны МДС насыщенных участков усиков зубцов. Для пазов статора его принимают равным:
сЭ1 = (tz1 – bш1)(1 – kδ). (9.266)
Вызванное насыщением от полей рассеяния уменьшение коэффициента магнитной проводимости рассеяния открытого паза (рис. 9.62, а)
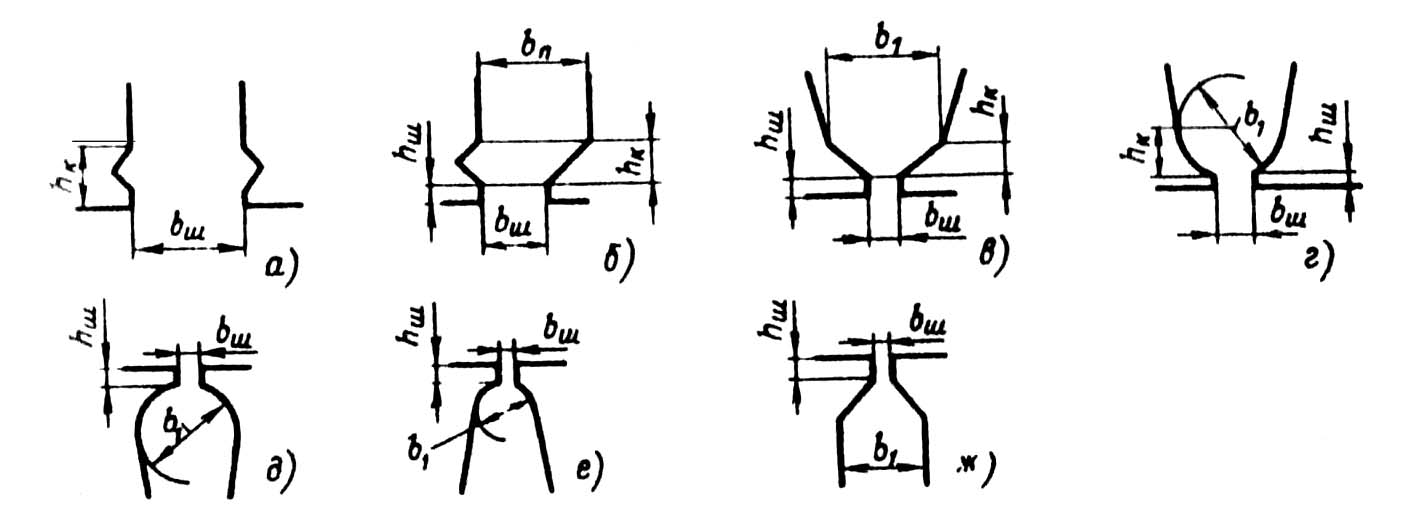
Рис. 9.62. К расчету влияния насыщения потоком рассеяния на
коэффициент магнитной проводимости паза:
а—ж — различные конфигурации верхней части пазов
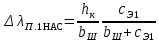(9.267)
Для полуоткрытых и полузакрытых пазов расчетная формула несколько усложняется из-за более сложной конфигурации их верхних клиновых частей. Для полуоткрытого паза (рис. 9.62, б)
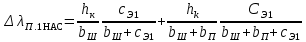(9.268)
Для полузакрытого паза (рис. 9.62, в, г)
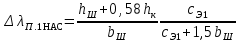(9.269)
Для фазных и короткозамкнутых роторов дополнительное раскрытие рассчитывают по формуле
сЭ2 = (t2 - bш )(1 - kδ). (9.270)
Уменьшение коэффициента проводимости для открытых и полузакрытых пазов ротора (рис. 9.62, д—ж)
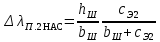(9.271)
Коэффициент магнитной проводимости пазового рассеяния при насыщении λп1нас определяют для статора по выражению
λп1нас = λп - Δλп1нас, (9.272)
где λп1 — проводимость, рассчитанная без учета насыщения.
Для ротора
λп2нас = λп2ξ - Δλп2нас, (9.273)
где λп2ξ — проводимость пазового рассеяния ротора для ненасыщенной зубцовой зоны с учетом влияния вытеснения тока.
Коэффициенты проводимости дифференциального рассеяния при насыщении участков зубцов статора λд1нас и ротора λД2нас
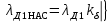(9.274)
Значения кδ принимают по кривым, представленным на рис. 9.61.
Индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния определяют по отношению сумм коэффициентов проводимости, рассчитанных без учета и с учетом насыщения от полей рассеяния:
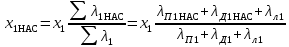(9.275)
Для ротора принимают отношения сумм проводимостей, рассчитанных без учета влияния насыщения и действия эффекта вытеснения тока (для номинального режима) и с учетом этих факторов:
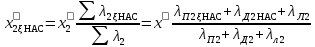(9.276)
Значения параметров x1нac и х2нас используют при расчете точек характеристик при скольжениях s ≥ sкp. Полученные для каждой из точек характеристики отношения токов, рассчитанных с учетом и без учета насыщения, сравнивают с принятыми коэффициентами kнас. Если расхождение превышает 10...15 %, то расчет для этого значения s повторяют, внося соответствующую корректировку в первоначально принимаемый коэффициент kнас.
Для круглых стержней (рис. 9.59, б)
kr = qс / qr = 1 + φ. (9.251)
Функция φкр для круглого стержня представлена на рис. 9.57.
Для грушевидных стержней (рис. 9.59, в)
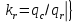(9.252)Площадь сечения qr при
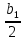≤ hr ≤ h1 +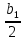 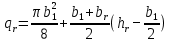, (9.253)где
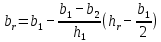
hr = hc / (l + φ).
При hr ≤ b1/2 площадь
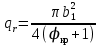(9.254)При hr > h1 + b1/2 принимают qr ≈ qc и kr = 1. Для трапецеидальных стержней с узкой верхней частью (см. рис. 9.59, г)
kr = qc /qr,
qс определяют по (9.252). Площадь qr при hr ≤ b1/2 определяют по (9.254) и при hr ≥ b1/2 — по (9.253), причем
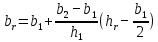(9.255)Для других конфигураций стержней kr, может быть определен из общего выражения kr = qc /qr с учетом размерных соотношений стержня и глубины проникновения тока в стержень hr.
Для расчета характеристик необходимо учитывать изменение сопротивления всей обмотки ротора r2 поэтому удобно ввести коэффициент общего увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока:
KR = r2ξ/r2, (9.256)
гдеr2ξ — сопротивление фазы короткозамкнутого ротора с учетом влияния эффекта вытеснения тока.
Выражение (9.256) легко преобразовать в более удобный для расчета вид:
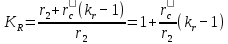(9.257)Для прямоугольных стержней это выражение приобретает вид
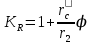. (9.258)В (9.257) и (9.258) для роторов без радиальных вентиляционных каналов с литой обмоткой (с прилегающими замыкающими кольцами) r'с = rс.
Для роторов с радиальными вентиляционными каналами и роторов с отставленными замыкающими кольцами
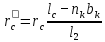
(9.259)
где lс — полная длина стержня, равная расстоянию между замыкающими кольцами, м; nк и bk — число и ширина, м, радиальных вентиляционных каналов; l2 — длина сердечника ротора, м.
Активное сопротивление фазы обмотки ротора с учетом вытеснения тока будет равно:
r2ξ = r2KR. (9.260)
Обозначив коэффициентом Кх изменение индуктивного сопротивления фазы обмотки ротора от действия эффекта вытеснения тока, получим
x2ξ = x2Kx, (9.261)
тогда
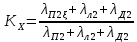(9.262)где λп2ξ — коэффициент магнитной проводимости пазового рассеяния с учетом эффекта вытеснения тока:
λп2ξ = λп2 - Δ λп2ξ
здесь
Δ λп2ξ = λ'п2 (1 – kД);
λ'п2 — коэффициент магнитной проводимости участка паза, занятого проводником с обмоткой (выражение для определения λ'п2 в формулах табл. 9.27 является множителем перед коэффициентом kд).
Влияние насыщения на параметры. В предыдущих параграфах рассматривались методы расчета параметров при допущении отсутствия насыщения стали магнитопровода полями рассеяния, магнитная проницаемость которой принималась равной бесконечности. При расчетах параметров холостого хода и рабочих режимов это допущение вполне оправдано, так как токи в этих режимах относительно малы и потоки рассеяния не создают заметного падения магнитного напряжения в стали зубцов. При увеличении скольжения свыше критического и в пусковых режимах токи в обмотках возрастают и потоки рассеяния увеличиваются. Коронки зубцов статора и ротора в машинах средней и большой мощности в большинстве случаев оказываются сильно насыщенными.
Насыщение коронок зубцов (рис. 9.60) приводит к увеличению магнитного сопротивления для части потока рассеяния, магнитные линии которого замыкаются через верхнюю часть паза. Поэтому коэффициент магнитной проводимости пазового рассеяния уменьшается. Несколько снижается также магнитная проводимость дифференциального рассеяния. На коэффициент магнитной проводимости лобового рассеяния насыщение стали потоками рассеяния влияния не оказывает.
Уменьшение потока пазового рассеяния из-за насыщения приближенно учитывают введением дополнительного раскрытия паза
, равного сэ. Дополнительное раскрытие сэ принимается таким, чтобы его магнитное сопротивление потоку рассеяния было равно магнитному сопротивлению насыщенных участков зубцов. При этом условии можно использовать для расчета коэффициент магнитной проводимости паза с учетом насыщения обычные формулы, предполагая, что μст = ∞. Уменьшение λп из-за насыщения участков зубцов
Рис. 9.60. Насыщение участков коронок Рис. 9.61. Функция Ks в зависимости
зубцов потоком рассеяния от фиктивной индукции Bδф
(Δλп.нас) будет определяться сэ. Таким образом, сэ зависит от уровня насыщения верхней части зубцов потоками рассеяния и, следовательно, от МДС паза, т. е. от тока в обмотке. Так как ток обмотки, в свою очередь, зависит от индуктивного сопротивления, определяемого магнитной проводимостью, то расчет приходится проводить методом последовательных приближений. Первоначально задаются предполагаемой кратностью увеличения тока, обусловленной уменьшением индуктивного сопротивления из-за насыщения зубцовой зоны:
kнас = Iнас / I,
где I — ток, рассчитанный для данного режима без учета насыщения; Iнас — ток в этом же режиме работы машины при насыщении участков зубцов полями рассеяния.
Ориентировочно для расчета пусковых режимов принимают kнас = 1,25...1,4; для режима максимального момента kнас = 1,1...1,2.
Для двигателей с открытыми пазами следует задаваться меньшими значениями kнас, при полузакрытых пазах — большими.
Расчет проводят в следующей последовательности. Определяют среднюю МДС обмотки, отнесенную к одному пазу обмотки статора:
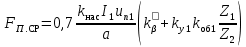(9.263)где I1 — ток статора, соответствующий расчетному режиму, без учета насыщения; а — число параллельных ветвей обмотки статора; uп1— число эффективных проводников в пазу статора;
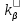— коэффициент, учитывающий уменьшение МДС паза, вызванное укорочением шага обмотки, рассчитывается по (9.156) или по (9.157); ky1 — коэффициент укорочения шага обмотки.По средней МДС F
п.cp рассчитывают фиктивную индукцию потока рассеяния в воздушном зазоре, Тл:
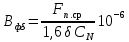(9.264)где коэффициент
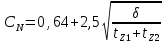(9.265)(tZ1 и tZ2 — зубцовые деления статора и ротора).
По полученному значению Bδф определяют отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом kδ, значение которого находят по кривой рис. 9.61.
Далее рассчитывают значения дополнительного эквивалентного раскрытия пазов статора и ротора (сЭ1 и сЭ2), магнитные напряжения которых будут эквивалентны МДС насыщенных участков усиков зубцов. Для пазов статора его принимают равным:
сЭ1 = (tz1 – bш1)(1 – kδ). (9.266)
Вызванное насыщением от полей рассеяния уменьшение коэффициента магнитной проводимости рассеяния открытого паза (рис. 9.62, а)
Рис. 9.62. К расчету влияния насыщения потоком рассеяния на
коэффициент магнитной проводимости паза:
а—ж — различные конфигурации верхней части пазов
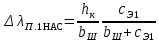(9.267)Для полуоткрытых и полузакрытых пазов расчетная формула несколько усложняется из-за более сложной конфигурации их верхних клиновых частей. Для полуоткрытого паза (рис. 9.62, б)
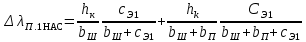(9.268)Для полузакрытого паза (рис. 9.62, в, г)
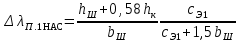(9.269)Для фазных и короткозамкнутых роторов дополнительное раскрытие рассчитывают по формуле
сЭ2 = (t2 - bш )(1 - kδ). (9.270)
Уменьшение коэффициента проводимости для открытых и полузакрытых пазов ротора (рис. 9.62, д—ж)
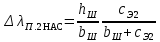(9.271)Коэффициент магнитной проводимости пазового рассеяния при насыщении λп1нас определяют для статора по выражению
λп1нас = λп - Δλп1нас, (9.272)
где λп1 — проводимость, рассчитанная без учета насыщения.
Для ротора
λп2нас = λп2ξ - Δλп2нас, (9.273)
где λп2ξ — проводимость пазового рассеяния ротора для ненасыщенной зубцовой зоны с учетом влияния вытеснения тока.
Коэффициенты проводимости дифференциального рассеяния при насыщении участков зубцов статора λд1нас и ротора λД2нас
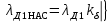(9.274)Значения кδ принимают по кривым, представленным на рис. 9.61.
Индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния определяют по отношению сумм коэффициентов проводимости, рассчитанных без учета и с учетом насыщения от полей рассеяния:
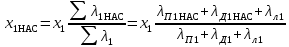(9.275)Для ротора принимают отношения сумм проводимостей, рассчитанных без учета влияния насыщения и действия эффекта вытеснения тока (для номинального режима) и с учетом этих факторов:
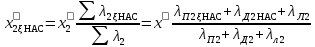(9.276)Значения параметров x1нac и х2нас используют при расчете точек характеристик при скольжениях s ≥ sкp. Полученные для каждой из точек характеристики отношения токов, рассчитанных с учетом и без учета насыщения, сравнивают с принятыми коэффициентами kнас. Если расхождение превышает 10...15 %, то расчет для этого значения s повторяют, внося соответствующую корректировку в первоначально принимаемый коэффициент kнас.