Файл: Общая теория связи.docx

Р 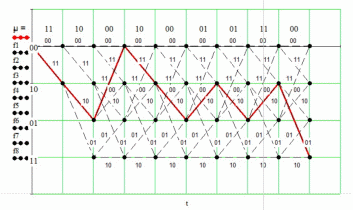ис.8 Расчет импульсной характеристикой кодера

Входные символы	1	0	0	0	0	0	0	0	0
Выходные символы	11	10	11	00	00	00	00	00	00

Следовательно, импульсная характеристика кодера h(k) = 111011000.
Определить кодовое расстояние d по известной импульсной характеристике кодера h(k) = 111011000.

Кодовое расстояние d=5, т.к. расстояние Хемминга между кодовой последовательностью 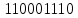и нулевой кодовой последовательностью равна 5, т.е. кодовое расстояние для сверточного кода, порождаемым кодером на рис. 8 , будет равно 5. Величина может быть также определена как число единичных символов в импульсной характеристике свёрточного кодера.

Расчётная диаграмма сверточного кодера.

1. 
   Р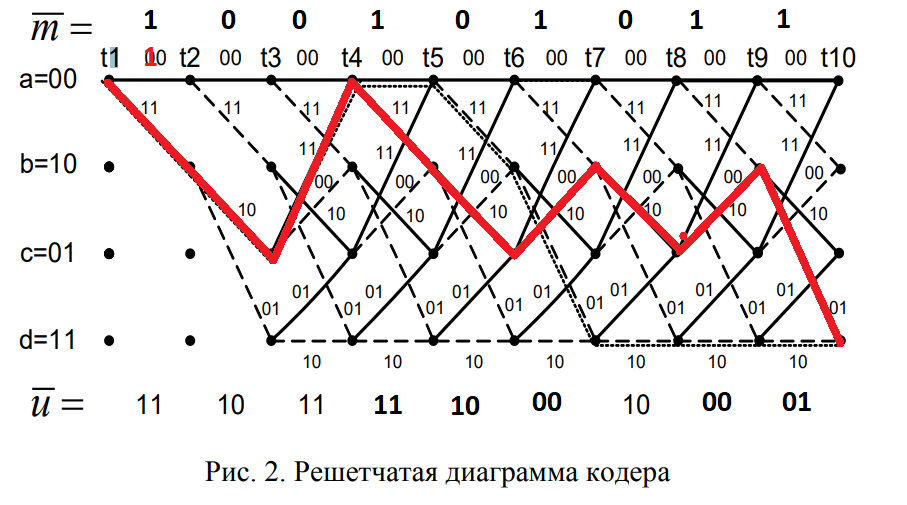 ешетчатая диаграмма сверточного кодера от момента времени t1 до момента t10:
   

Рис.9 Решетчатая диаграмма кодера
m - исходное сообщения, u – конечное сообщения.

m=100101011

u=11 10 11 11 10 00 10 00 01

---

3.4 Формирователь модулирующих символов

Формирователь модулирующих сигналов (ФМС) предназначен для преобразования двоичного цифрового потока от кодера C(t) в модулирующие сигналы I(t) и Q(t), которые необходимо подавать на синфазный и квадратурный входы модулятора для получения заданного сигнального созвездия на его выходе. Он должен содержать:

- регистр сдвига для деления входного потока бит от кодера на группы, передаваемые одним сигналом s_КАМ(t) (дибиты при QPSK и квадбиты при QASK);

- преобразователи уровней битовых сигналов (униполярной кодировки в биполярную: при QPSK «0» → h, «1» → –h; при QASK «00» → 3h, «01» → h, «10» → –h, «11» → –3h);

- дополнительно, при QASK, –кодопреобразователь исходного кода квадбит в код Грея для выравнивания минимальных расстояний между сигналами модулятора и соответствующим им квадбитам.

1. 
   Изображение сигнального созвездия для КАМ-16
   

Сигнальные созвездия четырехуровневойQASK



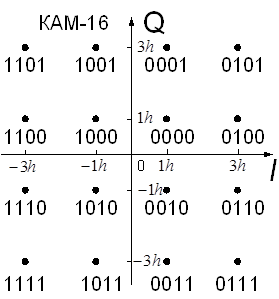
Рис.10 Сигнальное созвездие КАМ-16

2. 
   График реализации c(t) случайного процесса C(t)
   

на входе блока ФМС (выходе сверточного кодера) для первых 16 бинарных интервалов


Р 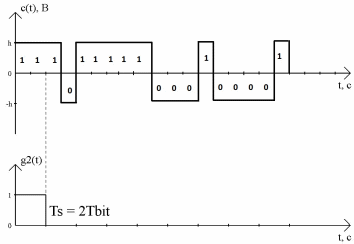ис.11 Осциллограмма реализации 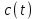с выхода свёрточного кодера.
Написать выражение для случайного процесса C(t) :

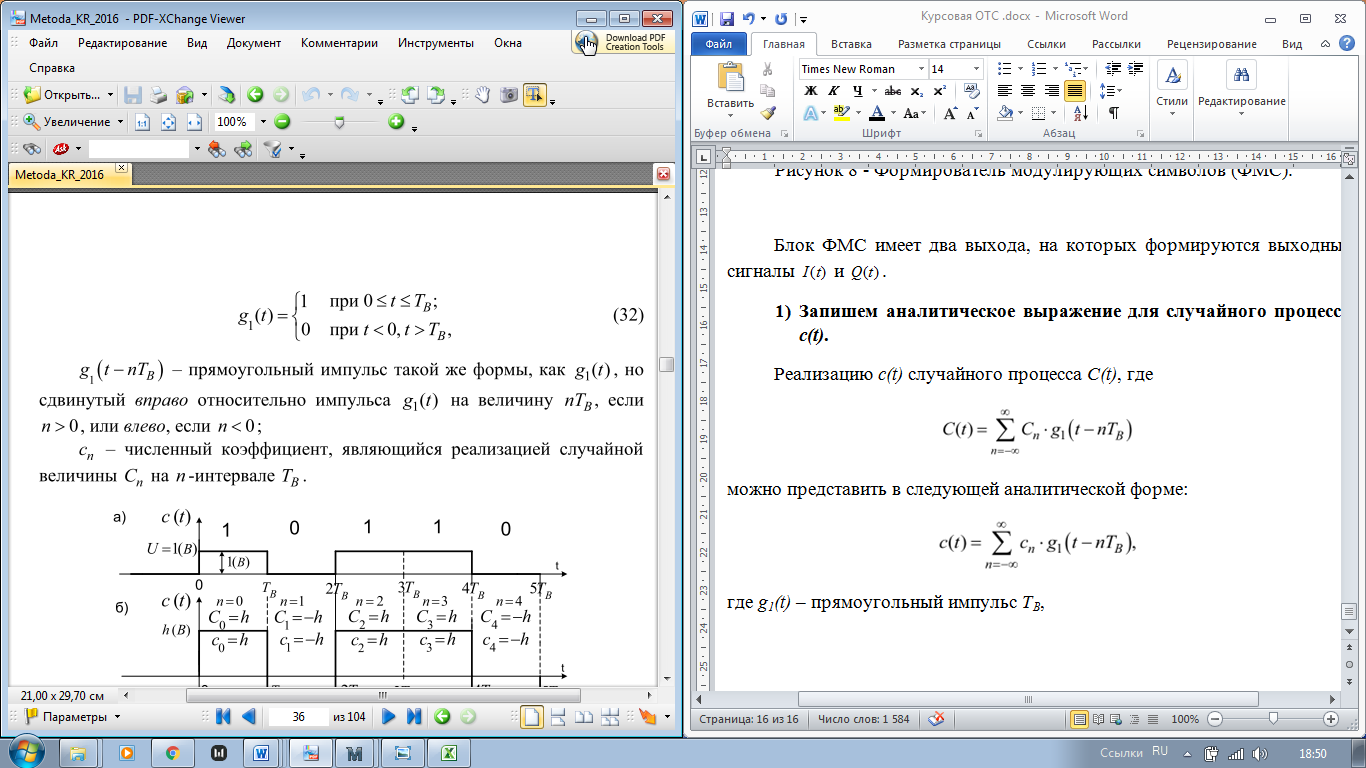
Реализацию c(t) случайного процесса C(t), где



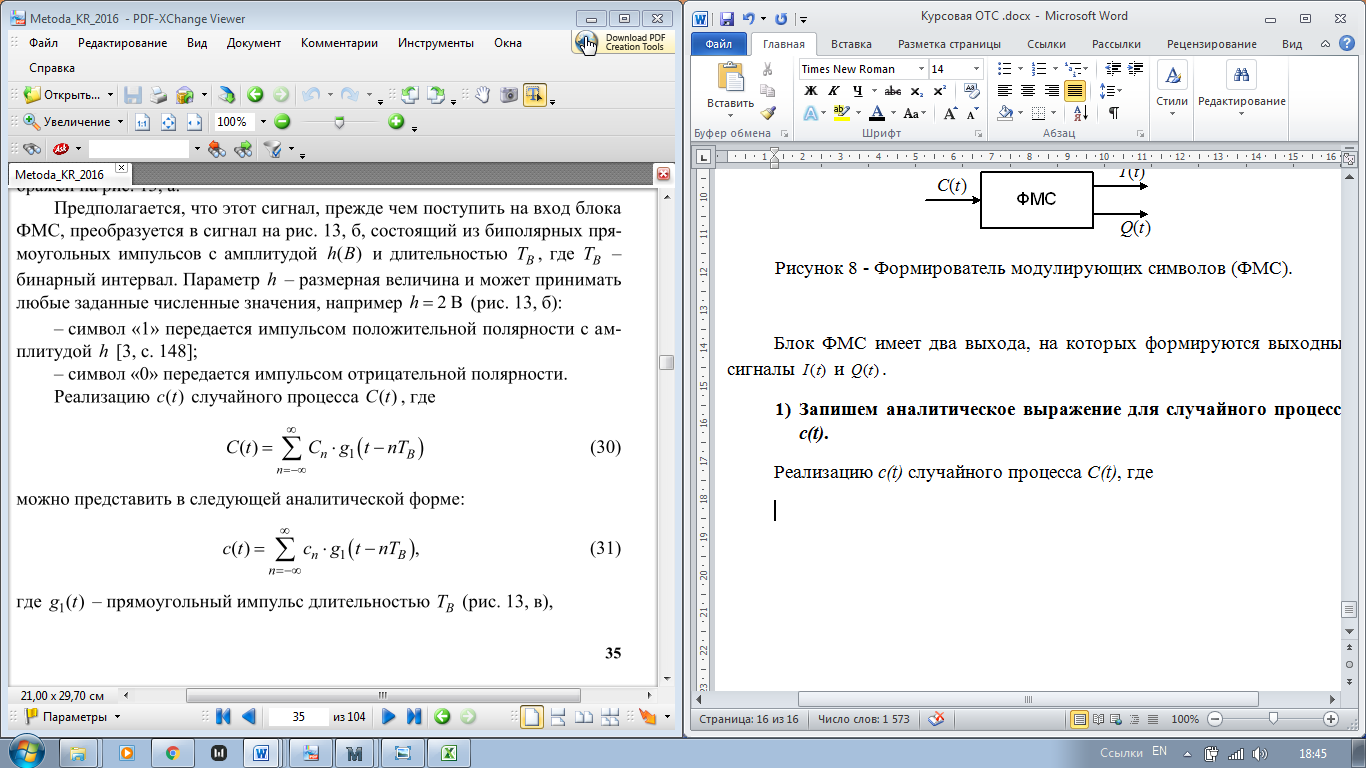
можно представить в следующей аналитической форме:



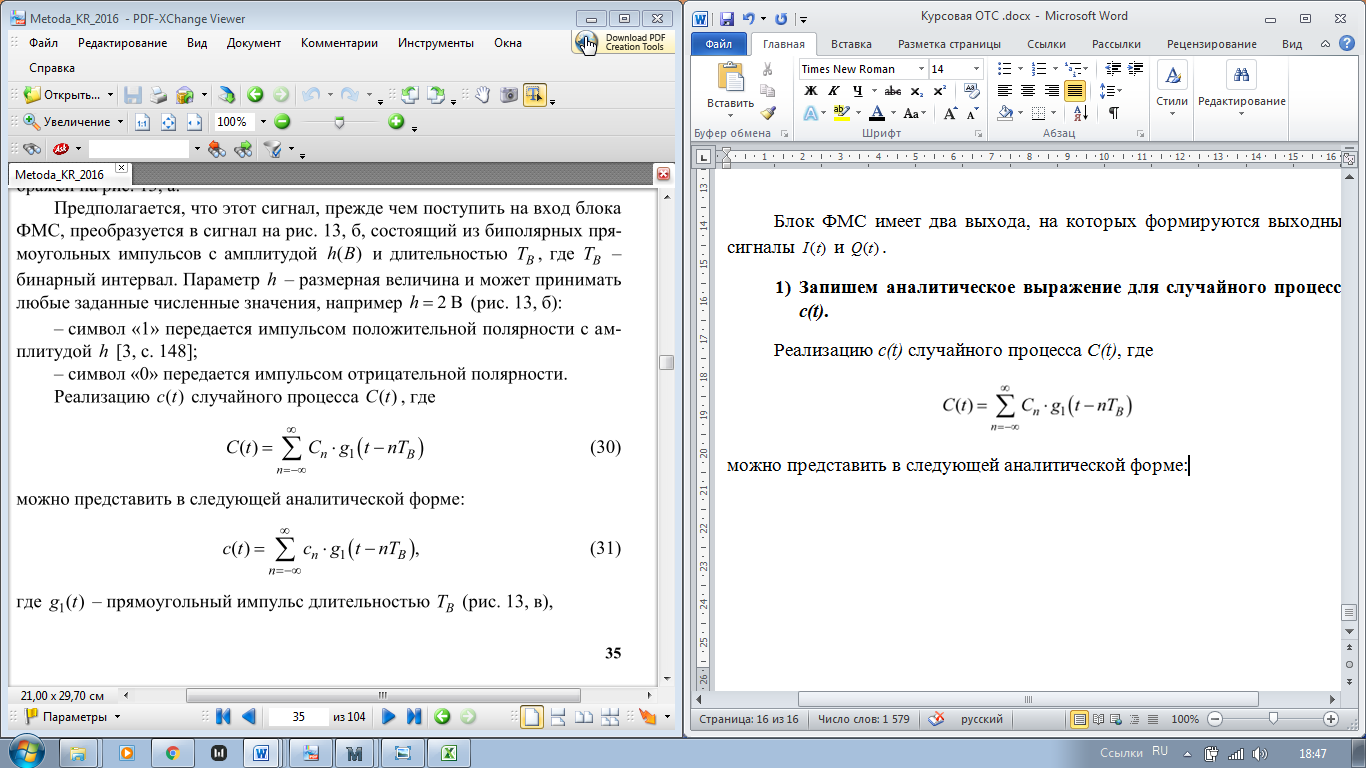
где g₁(t) – прямоугольный импульс T_B,



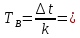3.326∙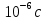
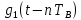– такой же формы, как g

---

₁(t), но сдвинутым вправо.

c_n – численный коэффициент, являющийся реализацией случайной величины C_n на n –интервале T_B

3. 
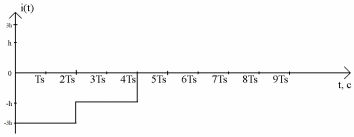
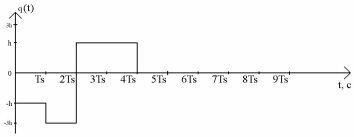
   Изображение графиков реализации i(t) и q(t) на выходе блока ФМС, соответствующие входной реализации c(t), в соответствии с сигнальным созвездием модулятора КФМ-4. Представление аналитических выражений для случайных процессов I(t) и Q(t).
   

Аналитическое выражение для случайных процессов I(t) и Q(t):


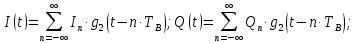
где 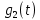– прямоугольный импульс длительностью 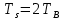= 3.326∙

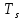- символьный интервал, 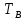– бинарный интервал,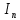 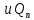– независимые случайные величины, заданные на символьном интервале с номером n, которые согласно сигнальному созвездию принимают дискретные значения -h, -h, h, -h с вероятностью 0,25 каждое.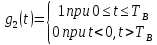



где 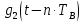– прямоугольный импульс такой же формы, как импульс 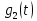, но сдвинутый вправо относительно импульса 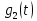на величину 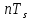, если 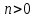, или влево, если .

4. 
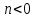   Аналитические выражения для корреляционной функции B_C(τ) и спектральной
   

плотности G(w) входного случайного процесса C(t) и построение их графиков.

Процесс C(t) является случайным синхронным сигналом. Его корреляционная функция имеет вид:

---

,

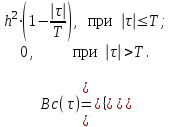а энергетический спектр

,

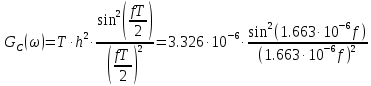где T=Tв - длительность тактового интервала, а h=0.5.



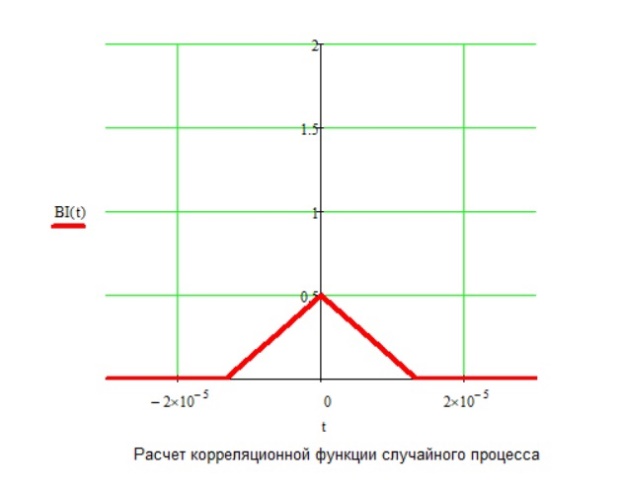
Рис.13 График корреляционной функции случайного процесса





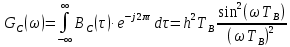
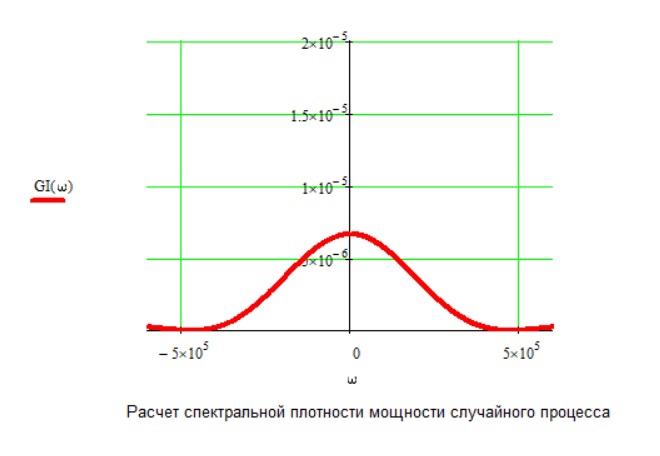
Рис.14 График спектральной плотности случайного процесса

1. 
   Написать аналитические выражения для корреляционных функцийB_I(τ) иB_Q(τ), спектральных плотностей мощности G_I() и G_Q() случайных процессов I(t)иQ(t). Построить графики этих функций.
   

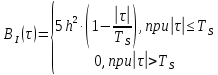
Случайный процесс Q(t) имеет такие же вероятностные характеристики, какие имеет процесс I(t), поэтому имеет место равенство:

B_Q(τ) = B_I(τ).



Используя теорему Винера – Хинчина и равенство B_Q(τ) = B_I(τ), получим:




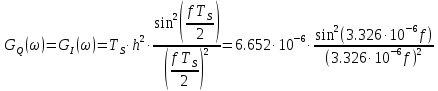
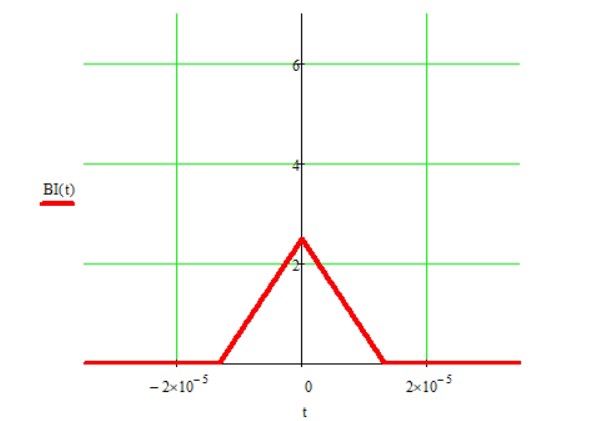
Рис.15 Графики корреляционный функций двух компонент случайного процесса



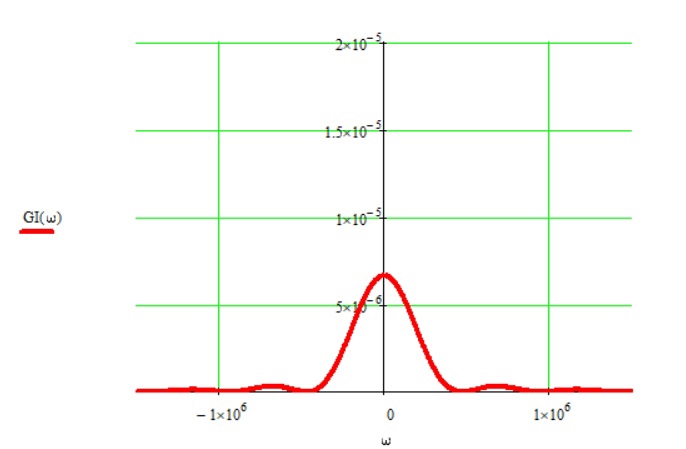
Рис.16 Графики двух спектральных плотностей для компонент случайного процесса

2. 
   Cравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС.
   

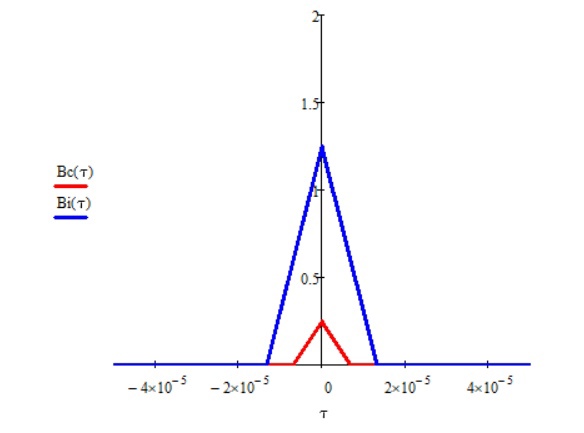
Рис.17 Сравнение графиков корреляционных функций на входе и на выходе ФМС



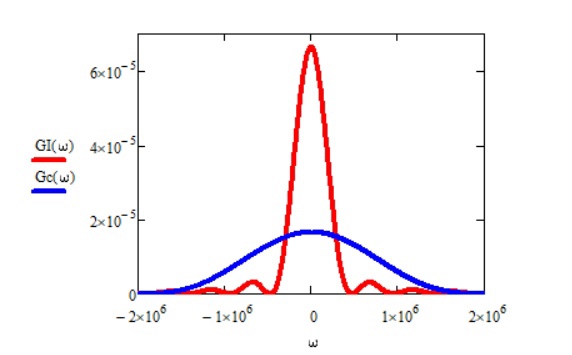
Рис.18 Сравнение графиков спектральных плотностей на входе и на выходе ФМС

Из приведенных графиков видно, что спектр выходных сигналов с блока ФМС уже, чем спектр входных сигналов. Сужение происходит из-за КФМ-4,при котором величина Т

---

_S=2 . Поэтому график функций G_I(ω) и G_Q(ω), оставаясь нефинитным, станет в 2 раза уже графика спектральной плотности мощности G_C(ω) процесса C(t).

---