Файл: Общая теория связи.docx

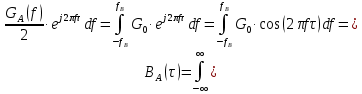
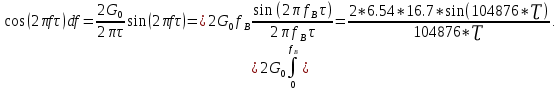
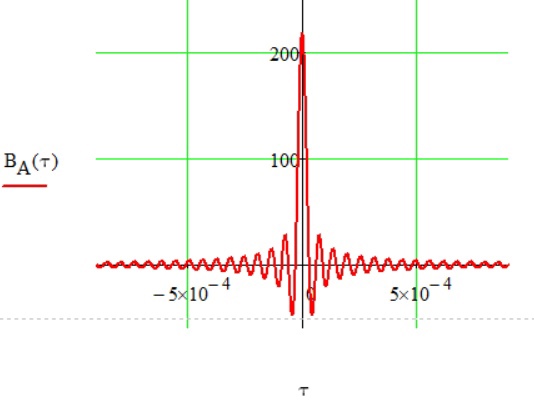
Рис. 5 Корреляционная функция

---

3.2. Аналого-цифровой преобразователь

Аналого-цифровой преобразователь (АЦП) преобразует реализации аналогового (непрерывного) сообщенияА(t) в цифровую форму – поток двоичных символов нулей и единиц, т. е. в последовательность прямоугольных импульсов, где «0» имеет нулевое напряжение, а «1» - прямоугольный импульс положительной полярности.

Преобразование аналогового сигнала в цифровую форму осуществляется в три этапа.

На первом этапе производится дискретизация реализации 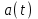сообщения 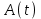по времени. В моменты времени 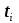берутся непрерывные по уровню отсчёты 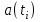мгновенных значений реализации 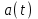. Расстояние между отсчётами равно интервалу 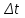, величина которого определяется в соответствии с теоремой Котельникова.

На втором этапе выполняется квантование точных отсчётов 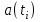по уровню. Для этого интервал 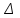равный разности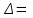 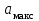- 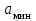разбивается на уровни квантования с постоянным шагом 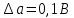. Уровни квантования нумеруются целыми числами 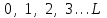-1. Нумерация уровней начинается с уровня, которому соответствует значение 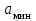, и заканчивается на уровне, которому соответствует значение 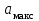. Каждый аналоговый отсчёт 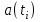заменяется значением ближайшего к нему уровня 0квантования

---

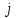в виде целого числа, удовлетворяющего неравенству 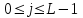. Получаем квантованный отсчёт 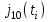в виде целого числа в десятичной форме счисления.

На третьем этапе число 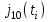в десятичной форме переводится в двоичную форму счисления 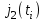в виде последовательности 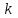двоичных символов и на выходе АЦП появляется сигнал в виде двоичной цифровой последовательности 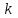информационных символов.

Расчёты:

1. 
   Интервал дискретизации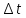 для получения 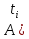) реализации A(t),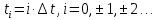
   

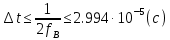
2. 
   Частоты дискретизации:
   

3. 
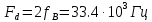
   Число уровней квантования L:
   

4. 
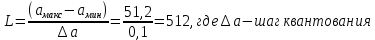
   Расчет мощности шума квантования:
   

5. 
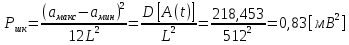
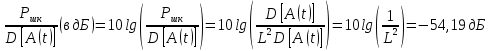
   Найти минимальное число k двоичных разрядов, требуемое для записи в двоичной форме любого номера j из L −1 номеров уровней квантования. Параметры подбираются так, чтобы L = 2^k, где k – разрядность АЦП, L = 2^k,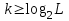 , где k – разрядность АЦП
   

k = log₂512 = 9

6. 
   Запись ­ разрядного двоичного числа, соответствующего заданному уровню квантования j:
   

j=299

7. 
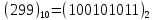
   Осциллограмма сигнала на выходе АЦП:
   

---

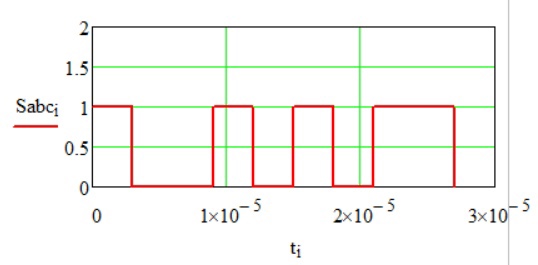
Рис.6 Осциллограмма на выходе АЦП

---

3.3. Кодер

Простейший двоичный сверточный кодер выполняет кодирование и образует модулирующий сигнал b(t). Последовательность символов на выходе кодера можно рассматривать как свертку импульсной характеристики кодера с выходной последовательностью информационных сигналов.



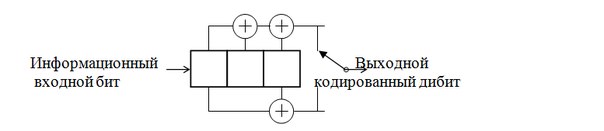
Рис.7 схема свёрточного кодера

Блочные коды (n,k) характеризуются двумя целыми числами n,k, где:

Параметры кодера:

k - количество информационных символов, поступающих на вход кодера в виде информационного блока; k=1 .

n - количество кодовых символов, поступающих с выхода кодера в виде кодового блока; n=2.

Целое число K, указывающее число разрядов (ячеек) в кодирующем регистре
сдвига, в которых находятся К – информационных символов и называется длиной кодового ограничения.

K- длина кодового ограничения; K=3.

Отношение 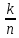называется степенью кодирования и является мерой добавленной избыточности; .

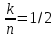Существует несколько способов описания связей между разрядами в регистре сдвига и сумматорами по модулю 2:
1. Один из этих способов заключается в определении n – векторов связи g1,g2,…,gn, где n – количество сумматоров в составе кодера. Каждый вектор имеет К составляющих из нулей и единиц, где К – длина кодового ограничения (количество разрядов в регистре сдвига) и описывает связь разрядов регистра сдвига кодера с соответствующим сумматором по модулю 2.
Единица (1) на i-ой позиции вектора означает, что разряд с номером i связан сумматором, а нуль (0) означает, что связи между разрядом с номером i и сумматором существует. Так, для кодера на рис.1 число сумматоров n=2 и будет вектор связи gi для верхнего сумматора и вектор связи g2 для нижнего сумматора. С учетом сказанного эти векторы связи будут иметь вид:
Векторы связи; g1 = 111 и g2 = 101.

Расчет импульсной характеристики кодера.

Реакция кодера на входной сигнал = 10000…. называется импульсной характеристикой кодера.

---