Добавлен: 09.11.2023
Просмотров: 283
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.5 Модулятор
В состав модулятора структурной схемы цифровой системы связи (ЦСС) между блоками ФМС и перемножителями входят сглаживающие формирующие фильтры СФФ, необходимые для оптимизации ЦЦС в отношении межсимвольной помехи, а также инвертор и сумматор, на выходе которого получается сигнал заданного вида модуляции КАМ-16.
-
Сглаживающий формирующий фильтр
-
Изобразить структурную схему модулятора в составе ЦСС.
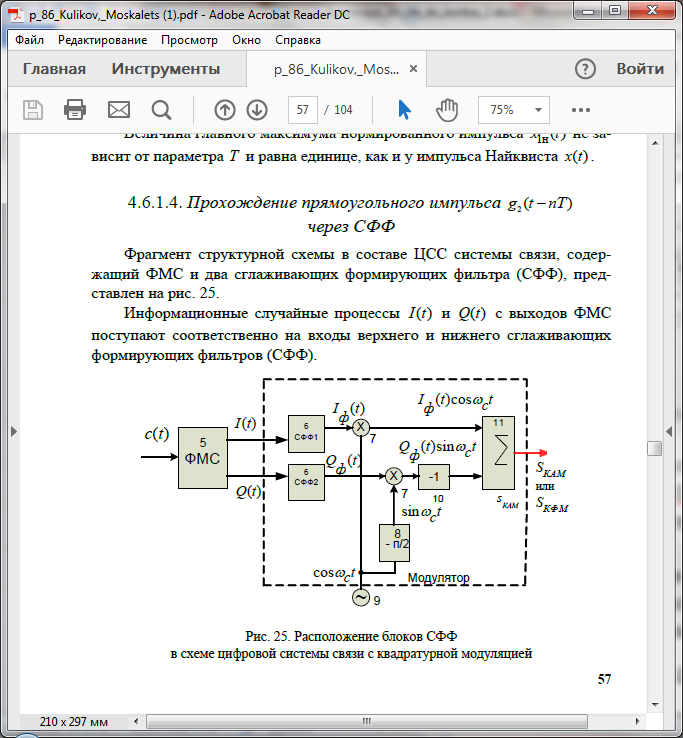
Рис.19 Схема модулятора в составе ЦСС
В состав модулятора входят блоки:
- генератор несущего колебания UcosωСt,
- фазовращатель на – 90º для получения квадратурного несущего колебания UsinωСt,
- перемножители, для получения БМ сигналов SI(t) = I(t)cosωСtи SQ(t) = Q(t)sinωСt, модулированных сигналами I(t) и Q(t), соответственно;
- сумматор для получения сигнала с квадратурной модуляцией SКАМ(t) = SI(t) + SQ(t) = I(t)cosωСt + Q(t)sinωСt = A(t)cos(ωСt – ψ) = A(t)cos(ωСt + φ),где
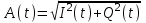 – огибающая, а φ = (–ψ)– фаза сигнала SКАМ(t); cosψ = I(t)/A(t) = cosφ, sinψ = Q(t)/A(t) = –sinφ.
– огибающая, а φ = (–ψ)– фаза сигнала SКАМ(t); cosψ = I(t)/A(t) = cosφ, sinψ = Q(t)/A(t) = –sinφ.-
Написать аналитические выражения для сигнала x(t) со «спектром приподнятого косинуса» (импульса Найквиста) и его спектральной плотности Sx(f) для значений коэффициента сглаживания 0 ≤ β ≤ 1. Изобразить их графики сигналов x(t) и соответствующие спектральные плотности.
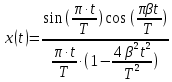
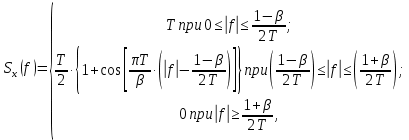
где β – коэффициент сглаживания (или ската), который может принимать значения в интервале 0 ≤ β ≤ 1.
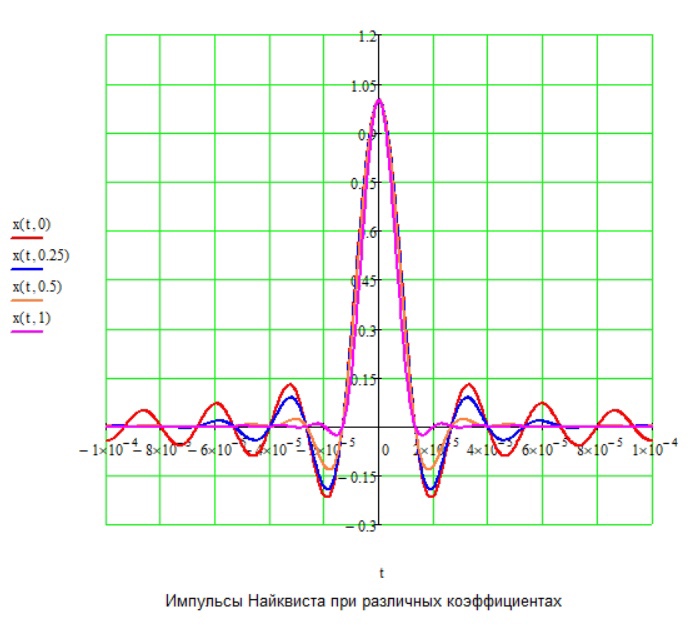
Рис.20 Импульс Найквиста с разным коэффициентом ß
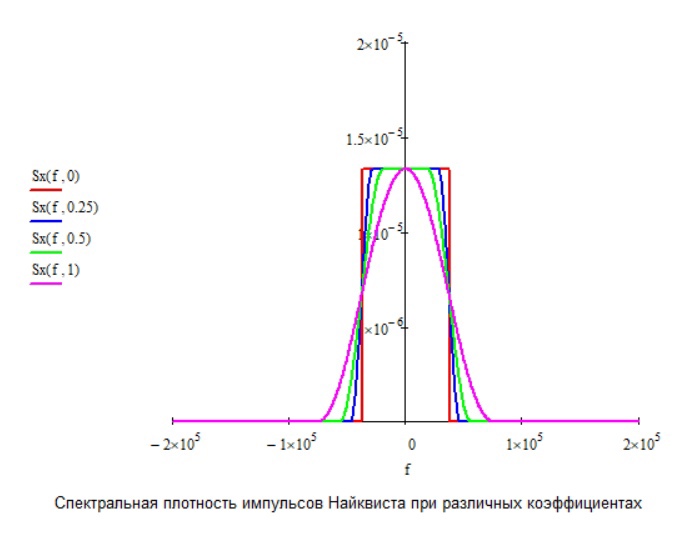
Рис.21 График спектральной плотности импульса Найквиста с разным коэффициентом ß
-
Изобразить графики спектральных плотностей Sx(f) и Sx1(f) сигналов x(t) и x1(t) (рис.17), где x(t) - импульс Найквиста при коэффициенте сглаживания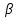 =1; x1(t) -импульс со спектральной плотности Sx1(f)=
=1; x1(t) -импульс со спектральной плотности Sx1(f)=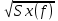 .
.
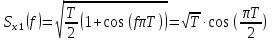
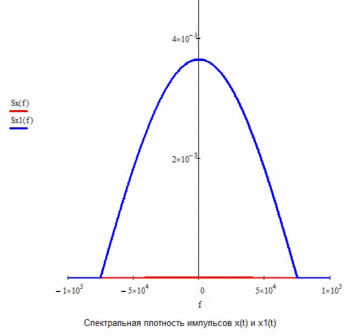
Рис.22 Сравнение графиков спектральный плотностей Sx(f) и Sx1(f)cигналов
-
На одном рисунке изобразить графики импульсов x(t)и x1(t). Выполняя обратное преобразование Фурье от известной функции Sx1(f), определим искомый импульс x1(t).
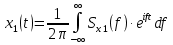
После элементарных преобразований получаем:
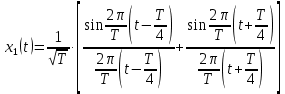
Величина главного максимума импульса x(t) равна единице, а величина главного максимума x1(t) зависит от параметра T и равна
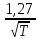 . И желательно от импульса x1(t)перейти к нормальному импульсу x1н(t).
. И желательно от импульса x1(t)перейти к нормальному импульсу x1н(t).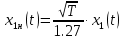
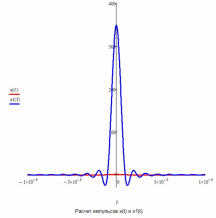
Рис.23 Сравнение графиков импульсов x(t)и x1(t)
-
Написать аналитическое выражение для случайных процессов Iф(t) и Qф(t).
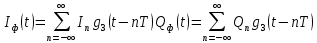 ,
,где
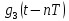 -детерминированный импульс, спектральная плотность, которого выражается через спектральную плотность импульса Нейквиста.
-детерминированный импульс, спектральная плотность, которого выражается через спектральную плотность импульса Нейквиста.-
Написать аналитическое выражение для корреляционных функций и спектральных плотностей случайных процессов Iф(t) и Qф(t), построить графики этих функций.
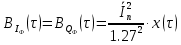
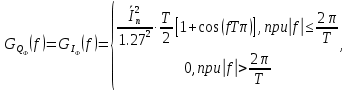
где
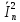 для КАМ-16 равен 5h2 .
для КАМ-16 равен 5h2 . 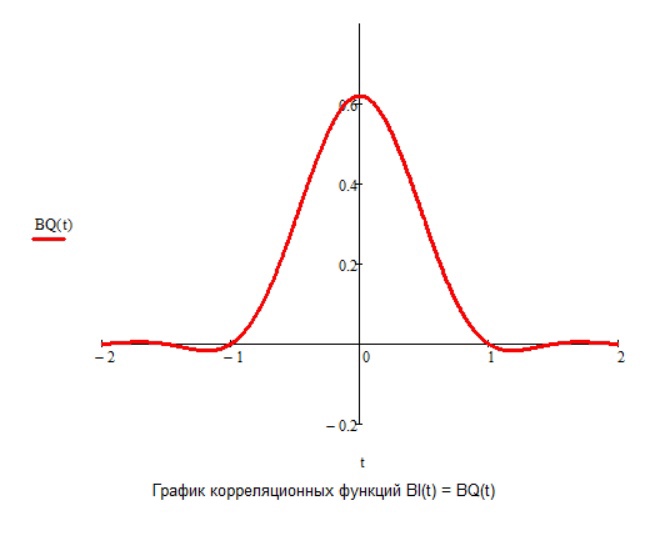
Рис.24 График корреляционных функций случайных процессов Iф(t) и Qф(t)
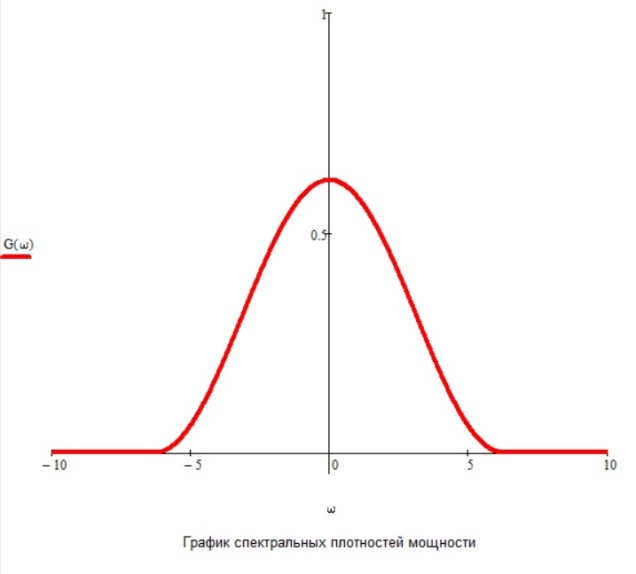
Рис.25 График спектральных плотностей случайных процессов Iф(t) и Qф(t)
-
Блоки перемножителей, инвертор, сумматор
Требуется:
-
Написать аналитические выражения для корреляционных функций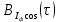 и
и 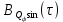 случайных процессов
случайных процессов 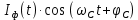 и
и 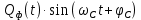 на выходах перемножителей, где
на выходах перемножителей, где 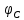 - случайная фаза с равномерной плотностью вероятности на интервале от 0…2
- случайная фаза с равномерной плотностью вероятности на интервале от 0…2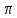 . Случайная фаза
. Случайная фаза 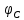 не зависит от случайных процессов
не зависит от случайных процессов 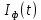 и
и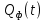 :
:
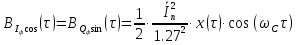
-
Написать аналитические выражения для корреляционных функций
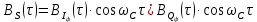
и для спектральной плотности мощности GS(ω) сигнала S(t) на выходе сумматора. Построить графики этих функций.
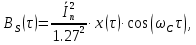
где x(
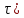 - импульс Найквиста при
- импульс Найквиста при 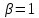 .
.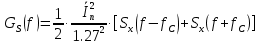
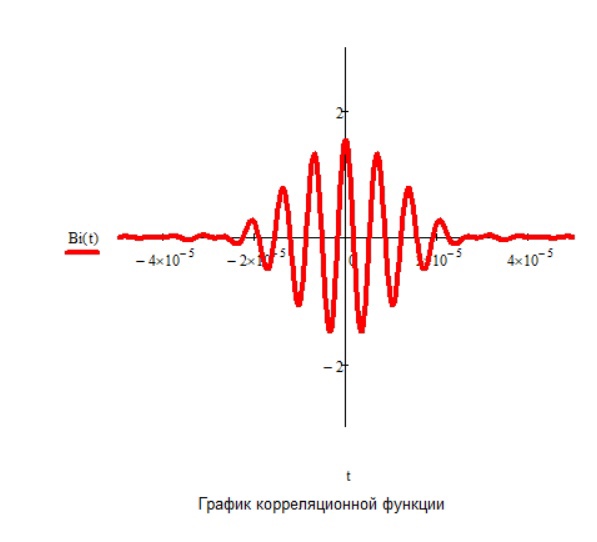
Рис.26 График корреляционной функции сигнала на выходе модулятора
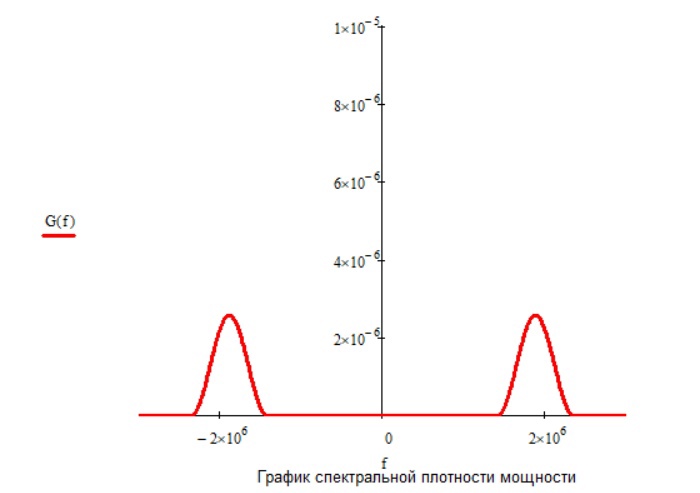
Рис.27 График спектральной плотности сигнала на выходе модулятора
3.6 Непрерывный канал
Передача сигналаS(t)происходит по непрерывному неискаженному каналу с постоянными параметрами в присутствии аддитивной помехи n(t) типа Гауссовского белого шума. Сигнал Z(t) на выходе такого канала имеет вид:
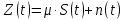
где
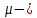 коэффициент передачи канала. Для всех вариантов принять
коэффициент передачи канала. Для всех вариантов принять 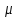 = 1.
= 1.Односторонняя спектральная плотность мощности помехи n(t) равна
N0=3
 10-7В2/Гц.
10-7В2/Гц.Требуется:
-
Определить минимальную ширину полосы частот Fkнепрерывного канала, необходимую для передачи по каналу сигнала S(t) с выхода модулятора.
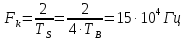
-
Определить Pc – среднюю мощность информационного сигнала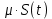 на выходе канала.
на выходе канала.
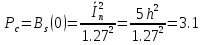 Вт
Вт-
Определить Pп – среднюю мощность помехи n(t) на выходе канала и найти отношение Pc/ Pп
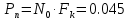 Вт
Вт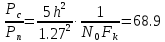
-
Рассчитать пропускную способность С (за секунду) непрерывного канала.
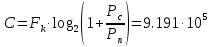 бит/с.
бит/с.3.7 Демодулятор
Требуется:
-
Изобразить структурную схему демодулятора.
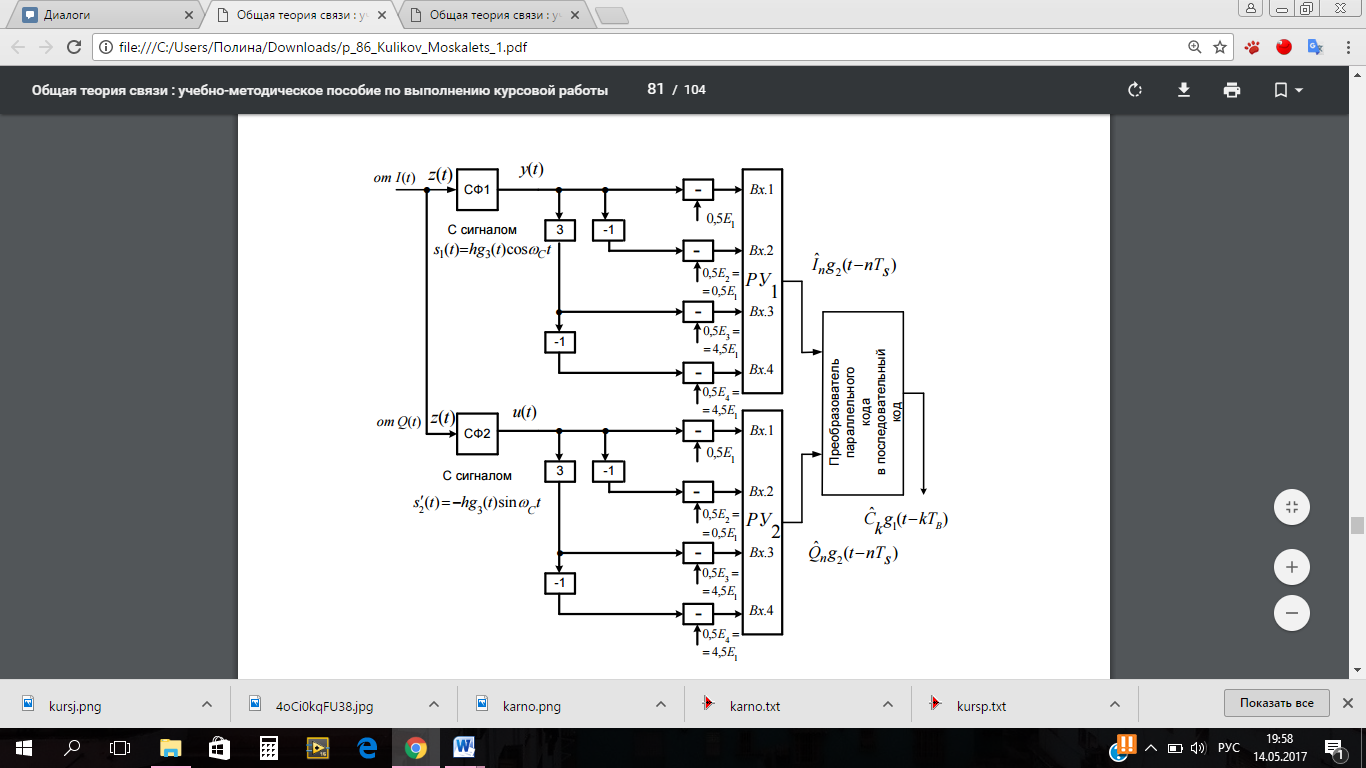
Рис.28 Схема демодулятора
-
Написать алгоритмы работы для решающих устройств РУ1 и РУ2 в составе когерентного демодулятора.
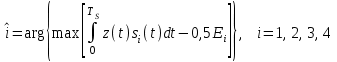 .
.В момент окончания каждого символьного интервала длительностью TS решающее устройство РУ1 (и РУ2) определяет номер входа
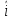 , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате
, на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате«00» при