Добавлен: 09.11.2023
Просмотров: 282
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=1, «10» при 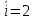 , «01» при
, «01» при 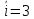 , «11» при
, «11» при 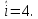
PIn=h(ош.п)=PIn=-h(ош.п)=PQn=h(ош.п)=PQn=-h(ош.п)
PIn=3h(ош.п)=PIn=-3h(ош.п)=PQn=3h(ош.п)=PQn=-3h(ош.п),
где PIn=x(ош) иPQn=x(ош) – вероятности ошибочного приема при In=xи Qn=x, соответственно.
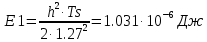
PIn=h(ош) = PIn=-h(ош) = PQn=h(ош) = PQn=-h(ош) =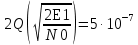
PIn=3h(ош) = PIn=-3h(ош) = PQn=3h(ош) = PQn=-3h(ош) =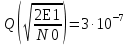
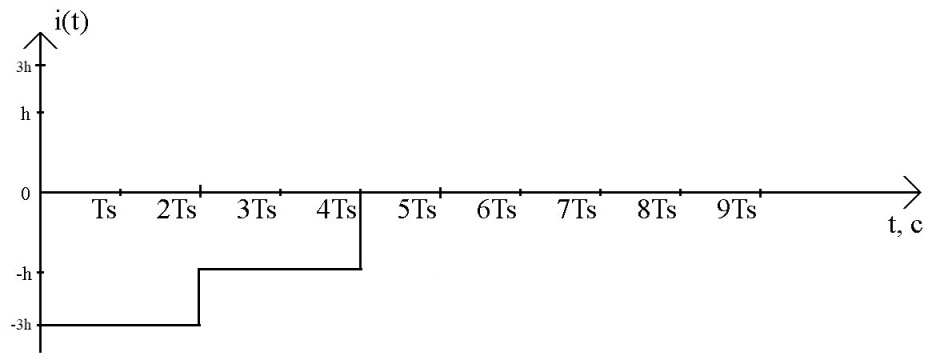
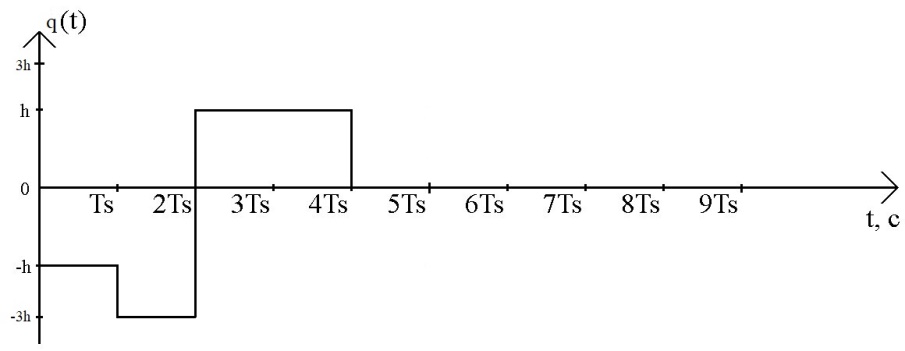
Рис.29 Осциллограмма сигнала на выходе РУ1 и РУ2
PIn=h,Qn=h(ош) = PIn=h(ош) + PQn=h(ош) – PIn=h(ош)·PQn=h(ош)=10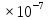
PIn=3h,Qn=3h(ош) = PIn=3h(ош) + PQn=3h(ош) – PIn=3h(ош)·PQn=3h(ош)=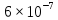
PIn=3h,Qn=h(ош) = PIn=3h(ош) + PQn=h(ош) – PIn=3h(ош)·PQn=h(ош)=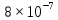
Pcp(ош)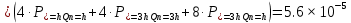
Требуется:
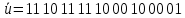
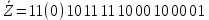
Числа над ребрами решетки декодера определяются, как расстояния Хемминга между двумя символами принятой последовательности z , расположенными над данным ребром, и двумя символами, которыми отмечено данное ребро на решетке кодера.
Целью алгоритма Витерби является то, что из двух путей, приходящих в каждый из узлов выжившим считается только один – тот путь, которому соответствует меньшая метрика.
Шаг 1

Gqw = 1
Gqp = 1
Шаг 2
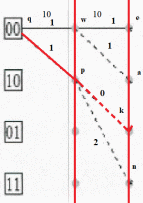
Gqpk = 1 + 0 = 1
Gqwe = 1 + 1 = 2
Gqwa = 1 + 1 = 2
Gqpn = 1 + 2 = 3
Шаг 3
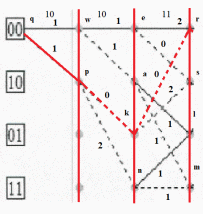
Gqpkr = 1 + 0 + 0 = 1
Gqpks = 1 + 0 + 2 = 3
Gqwer = 1 + 1 + 2 = 4
Gqwai = 1 + 1 + 1 = 3
Gqwes = 1 + 1 + 0 = 2
Gqwam= 1 + 1 + 1 = 3
Gqpnm = 1 + 2 + 1 = 4
Gqpni = 1 + 2 + 1 = 4
Шаг 4
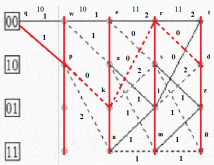
Gqpkrd = 1 + 0 + 0 + 0 = 1
Gqwesz = 1 + 1 + 0 + 1 = 3
Gqwesй = 1 + 1 + 0 + 1 = 3
Gqpkrt = 1 + 0 + 0 + 2 = 3
Gqpksz = 1 + 0 + 2 + 1 = 4
Gqpksй = 1 + 0 + 2 + 1 = 4
Gqwait = 1 + 1 + 1 + 0 = 3
Gqwaid = 1 + 1 + 1 + 2 = 5
Gqwamz= 1 + 1 + 1 + 1 = 4
Gqwamй= 1 + 1 + 1 + 1 = 4
Шаг 5
G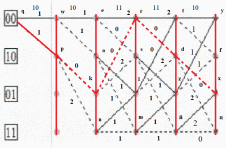 qpkrdx = 1 + 0 + 0 + 0 + 0 = 1
qpkrdx = 1 + 0 + 0 + 0 + 0 = 1
Gqpkrdц = 1 + 0 + 0 + 0 + 2 = 3
Gqweszy = 1 + 1 + 0 + 1 + 1 = 4
Gqweszf = 1 + 1 + 0 + 1 + 1 = 4
Gqwesйx = 1 + 1 + 0 + 1 + 2 = 5
Gqwesйц = 1 + 1 + 0 + 1 + 0 = 3
Gqpkrty = 1 + 0 + 0 + 2 + 1 = 4
Gqpkrtf = 1 + 0 + 0 + 2 + 1 = 3
Gqwaity = 1 + 1 + 1 + 0 + 1 = 4
Gqwaitf = 1 + 1 + 1 + 0 + 1 = 4
Шаг 6
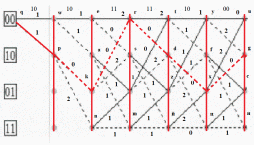
Gqpkrdxu = 1 + 0 + 0 + 0 + 0 + 2 = 3
Gqpkrdxg = 1 + 0 + 0 + 0 + 0 + 0 = 1
Gqpkrdцc = 1 + 0 + 0 + 0 + 2 + 1 = 4
Gqpkrdци = 1 + 0 + 0 + 0 + 2 + 1 = 4
Gqwesйцc = 1 + 1 + 0 + 1 + 0 + 1 = 4
Gqwesйци = 1 + 1 + 0 + 1 + 0 + 1 = 4
Gqpkrtfc = 1 + 0 + 0 + 2 + 1 + 1 = 5
Gqpkrtfи = 1 + 0 + 0 + 2 + 1 + 1 = 5
Шаг 7
G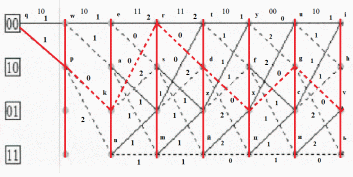
qpkrdxuh = 1 + 0 + 0 + 0 + 0 + 2 + 1 = 4
Gqpkrdxui = 1 + 0 + 0 + 0 + 0 + 2 + 1 = 4
Gqpkrdxgv
= 1 + 0 + 0 + 0 + 0 + 0 + 0 = 1
Gqpkrdxgь = 1 + 0 + 0 + 0 + 0 + 0 + 2 = 3
Шаг 8
Gqpkrdxgvo = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 2 = 3
Gqpkrdxgvj = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 1
Gqpkrdxgьb = 1 + 0 + 0 + 0 + 0 + 0 + 2 + 1 = 4
Gqpkrdxgьч = 1 + 0 + 0 + 0 + 0 + 0 + 2 + 1 = 4
Шаг 9
Gqpkrdxgvoд = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 2 + 1 = 3
Gqpkrdxgvoз = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 2 + 1 = 3
Gqpkrdxgvjг = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 1
Gqpkrdxgvjя = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 2
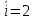 , «01» при
, «01» при 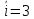 , «11» при
, «11» при 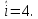
-
Определение вероятности ошибок на выходах РУ1 и РУ2 при определении значений символов Inи Qn(равных h, -h, 3h, -3h):
PIn=h(ош.п)=PIn=-h(ош.п)=PQn=h(ош.п)=PQn=-h(ош.п)
PIn=3h(ош.п)=PIn=-3h(ош.п)=PQn=3h(ош.п)=PQn=-3h(ош.п),
где PIn=x(ош) иPQn=x(ош) – вероятности ошибочного приема при In=xи Qn=x, соответственно.
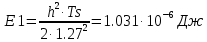
PIn=h(ош) = PIn=-h(ош) = PQn=h(ош) = PQn=-h(ош) =
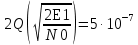
PIn=3h(ош) = PIn=-3h(ош) = PQn=3h(ош) = PQn=-3h(ош) =
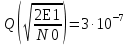
-
На четырех символьных интервалах длительностью TS нарисовать сигналы на выходах РУ1 и РУ2 демодулятора, соответствующие сигналам на выходе блока ФМС.


Рис.29 Осциллограмма сигнала на выходе РУ1 и РУ2
-
Определить вероятности ошибок PIn=h, Qn=h(ош.п) на выходе преобразователя параллельного кода в последовательный код, если In=h и Qn=h, где PIn=h, Qn=h (ош.п) – обозначение вероятности ошибочного приема.
PIn=h,Qn=h(ош) = PIn=h(ош) + PQn=h(ош) – PIn=h(ош)·PQn=h(ош)=10
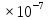
PIn=3h,Qn=3h(ош) = PIn=3h(ош) + PQn=3h(ош) – PIn=3h(ош)·PQn=3h(ош)=
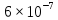
PIn=3h,Qn=h(ош) = PIn=3h(ош) + PQn=h(ош) – PIn=3h(ош)·PQn=h(ош)=
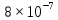
-
Определить среднюю вероятность ошибки на выходе преобразователя при условии, что имеют место равенства.
Pcp(ош)
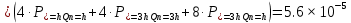
3.8 Декодер
Требуется:
-
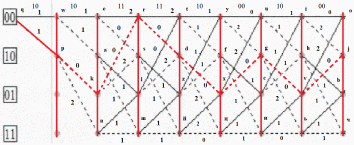
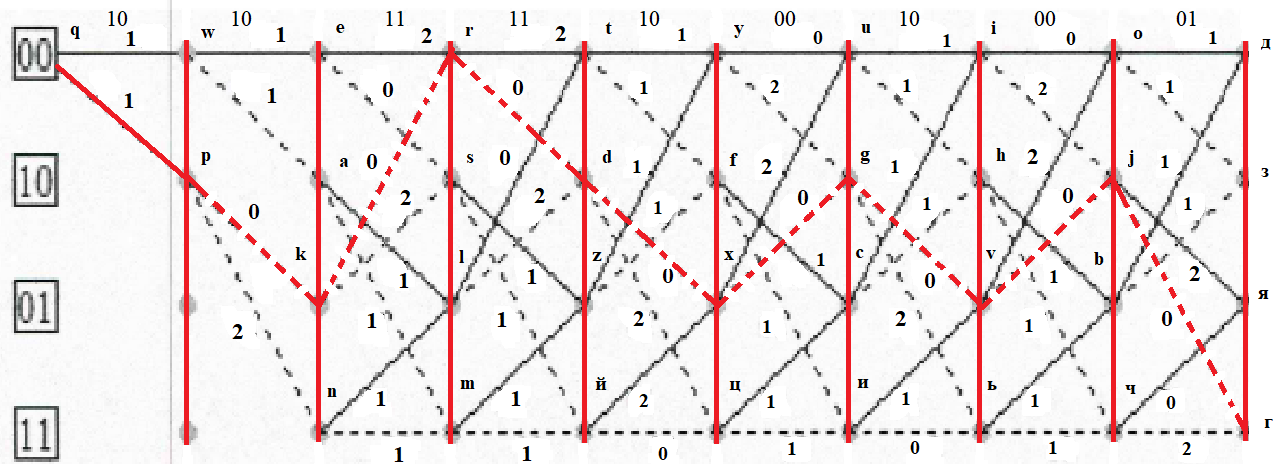
Построить решетчатую диаграмму декодера последовательности по аналогии с решетчатой диаграммой кодера. Численные обозначения над ребрами решетчатой диаграммы декодера определяются с учетом последовательности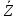 своего варианта.
своего варианта. -
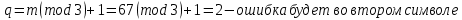
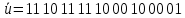
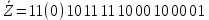
Числа над ребрами решетки декодера определяются, как расстояния Хемминга между двумя символами принятой последовательности z , расположенными над данным ребром, и двумя символами, которыми отмечено данное ребро на решетке кодера.
Целью алгоритма Витерби является то, что из двух путей, приходящих в каждый из узлов выжившим считается только один – тот путь, которому соответствует меньшая метрика.
Шаг 1

Gqw = 1
Gqp = 1
Шаг 2

Gqpk = 1 + 0 = 1
Gqwe = 1 + 1 = 2
Gqwa = 1 + 1 = 2
Шаг 3

Gqpkr = 1 + 0 + 0 = 1
Gqpks = 1 + 0 + 2 = 3
Gqwai = 1 + 1 + 1 = 3
Gqwes = 1 + 1 + 0 = 2
Gqwam= 1 + 1 + 1 = 3
Шаг 4

Gqpkrd = 1 + 0 + 0 + 0 = 1
Gqwesz = 1 + 1 + 0 + 1 = 3
Gqwesй = 1 + 1 + 0 + 1 = 3
Gqpkrt = 1 + 0 + 0 + 2 = 3
Gqwait = 1 + 1 + 1 + 0 = 3
Шаг 5
G
 qpkrdx = 1 + 0 + 0 + 0 + 0 = 1
qpkrdx = 1 + 0 + 0 + 0 + 0 = 1Gqpkrdц = 1 + 0 + 0 + 0 + 2 = 3
Gqwesйц = 1 + 1 + 0 + 1 + 0 = 3
Gqpkrtf = 1 + 0 + 0 + 2 + 1 = 3
Шаг 6

Gqpkrdxu = 1 + 0 + 0 + 0 + 0 + 2 = 3
Gqpkrdxg = 1 + 0 + 0 + 0 + 0 + 0 = 1
Шаг 7

Gqpkrdxgv
= 1 + 0 + 0 + 0 + 0 + 0 + 0 = 1
Gqpkrdxgь = 1 + 0 + 0 + 0 + 0 + 0 + 2 = 3
Шаг 8

Gqpkrdxgvo = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 2 = 3
Gqpkrdxgvj = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 1
Шаг 9

Gqpkrdxgvjг = 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 1