Добавлен: 09.11.2023
Просмотров: 291
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Факультет фундаментальной подготовки
Кафедра теоретических основ телекоммуникаций
________________________________________________________________
Курсовая работа
по дисциплине «Общая теория связи»
Выполнил
студ. 2 курса, гр. ИКТ3-15
Малахов Максим Юрьевич
№ зачетной книжки
2105267
направление подготовки 11.03.02
____________
«___»________ 2023
Принял
Виноградов Виталий Борисович
_____________
оценка
___________
«___»________ 2023
Санкт-Петербург,
2023
Введение
Цель курсовой работы (КР) - изучить принципы работы системы цифровой передачи аналоговых сообщений и рассчитать основные характеристики входящих в неё функциональных узлов.
Задание: изучить и разработать систему цифровой связи, оптимальную в отношении флуктуационной помехи и исключающую появление межсимвольной помехи.
Требуется
-
Изобразить структурную схему системы цифровой связи, включив блоки сглаживающих формирующих фильтров СФФ1 и СФФ2 в передающем устройстве и согласованных фильтров СФ1 и СФ2 в приёмном устройстве. -
Пояснить назначение всех функциональных узлов системы цифровой связи. -
Рассчитать основные характеристики системы передачи цифровой информации.
Исходные данные
Цель: Изучить и разработать систему цифровой связи, оптимальную в отношении флотационной помехи и исключающую появления межсимвольной помехи.
| Параметр | Данные по моему варианту |
| Предельные уровни аналогового сигнала 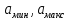 (В) (В) | 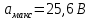 |
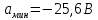 | |
| Верхняя частота спектра аналогового сигнала 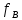 | 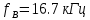 |
| Заданный уровень квантования | 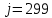 |
| Спектральная плотность мощность флуктуационной помехи | 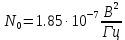 |
| q- номер тактового интервала ошибки | 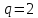 |
| Вид модуляции | КАМ-16 |
1. Структурная схема системы цифровой связи
Система связи предназначена для передачи аналоговых сообщений по цифровому каналу связи.
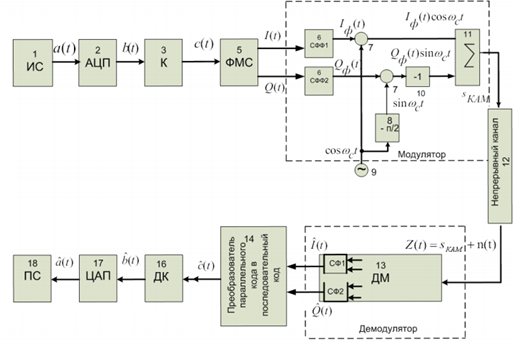
Рис.1 Структурная схема системы цифровой связи
Структурная схема системы цифровой связи.
Входящие в систему цифровой связи функциональные узлы:
1 – источник сообщений;
2 – аналого-цифровой преобразователь (АЦП);
3 – кодер (К);
5 – формирователь модулирующих символов (ФМС) или преобразователь последовательного кода в параллельный код;
6 – сглаживающие формирующие фильтры (СФФ1, СФФ2);
7 – перемножители;
8 – фазовращатель;
9 – генератор гармонических колебаний;
10 – инвертор;
11 – сумматор;
12 – непрерывный канал;
13 – демодулятор (ДМ);
14 – преобразователь параллельного кода в последовательный код;
16 – декодер (ДК);
17 – цифро-аналоговый преобразователь (ЦАП);
18 – получатель сообщений.
2. Расчет системы цифровой связи
3.1. Источник сообщений


ИС
A(t) a(t)
Источник сообщения (ИС) вырабатывает реализации a(t) стационарного случайного процесса A(t)типа квазибелого шума с параметрами
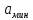 ,
,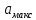 и
и  . Мгновенные значения сообщения равновероятны в интервале от значения
. Мгновенные значения сообщения равновероятны в интервале от значения 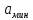 до значения
до значения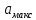 .
.Требуется:
-
Написать аналитические выражения для плотности вероятности w(a) мгновенных значений сообщения, функции распределения F(a) и построить их графики. -
Рассчитать математическое ожидание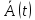 и дисперсию D{A(t)} сообщенияA(t).
и дисперсию D{A(t)} сообщенияA(t). -
Написать аналитическое выражение для спектральной плотности мощности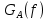 сообщения A(t)и построить график.
сообщения A(t)и построить график. -
Найти аналитическое выражение для корреляционной функции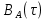 сообщения A(t) и построить график. По форме графика
сообщения A(t) и построить график. По форме графика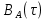 определить, является ли сообщение A(t) эргодическим случайным процессом или не является таковым.
определить, является ли сообщение A(t) эргодическим случайным процессом или не является таковым.
0
Ход работы:
-
Для нахождения одномерной плотности вероятности мгновенных значений случайного
процесса a(t) учтем, что все его мгновенные значения в заданном интервале равновероятны, и, следовательно, плотность вероятности будет постоянна в этом интервале и равна нулю вне этого интервала.
Значение плотности вероятности внутри интервала от
 до
до  определим из условия нормировки:
определим из условия нормировки: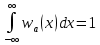

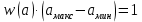
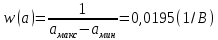
Таким образом, аналитическое выражение для плотности распределения вероятности случайного процесса а(t) имеет вид:
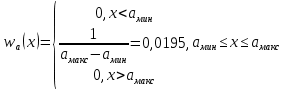
Тогда построим график одномерного закона распределения плотности вероятности мгновенных значений случайного процессаa(t):
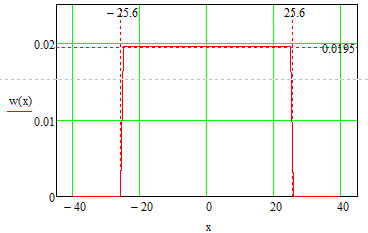
Рис. 2 Распределение плотности вероятности
Функция распределения F(a) связана с плотностью распределения интегральным соотношением:
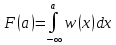
При
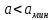 значение плотности вероятности
значение плотности вероятности 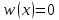 , следовательно,
, следовательно, 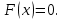
При
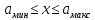 значение функции распределения будет находиться следующим образом (∆ =
значение функции распределения будет находиться следующим образом (∆ = 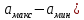 :
: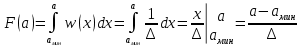
При
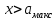 значение функции распределения будет находиться как:
значение функции распределения будет находиться как: 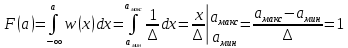
Cоставим систему
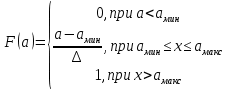
Подставляя числовые значения, получим функцию распределения:
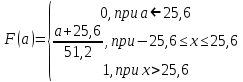
Тогда построим график одномерного закона распределения вероятности мгновенных значений случайного процессаa(t):
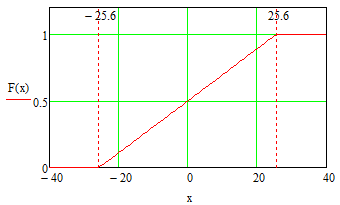
Рис. 3 Функция распределения
-
Найдем математическое ожидание М случайного процесса a(t):
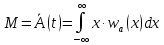
Так как w(a) вне интервала от
 до
до  равна нулю, то получим:
равна нулю, то получим: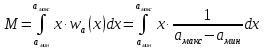
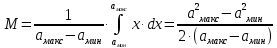
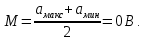
То есть получили, что среднее значение случайного процесса a(t) равно 0 В.
Найдем дисперсию или математическое ожидание квадрата D случайного процесса a(t):
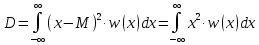
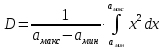
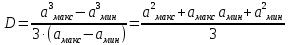 =
=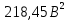
-
Постоянная составляющая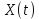 процесса:
процесса:
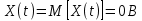
Мощность
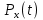 переменной составляющей процесса:
переменной составляющей процесса: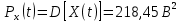
Спектральная плотность средней мощности имеет равномерное распределение в интервале частот от 0 до
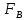 величиной.
величиной.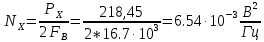
Функция спектральной плотности мощности будет иметь вид:
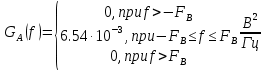
График энергетического спектра
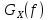 :
: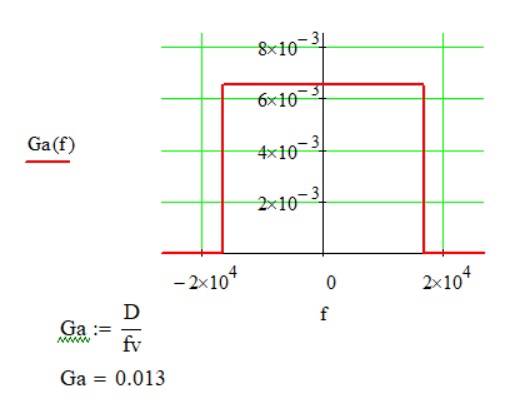
Рис. 4 Энергетический спектр
-
Корреляционную функцию случайного процесса можно определить через его энергетический спектр по теореме Винера-Хинчина.
Теорема Винера-Хинчина – связь между энергетическим спектром и корреляционной функцией:
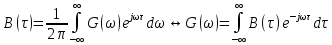
Корреляционную функцию случайного процесса: