Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 144
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
соответствуют угловым скоростям (частотам вращения) колёс 1, 2, … (рис. 87). При этом схема редуктора вычерчивается в масштабе 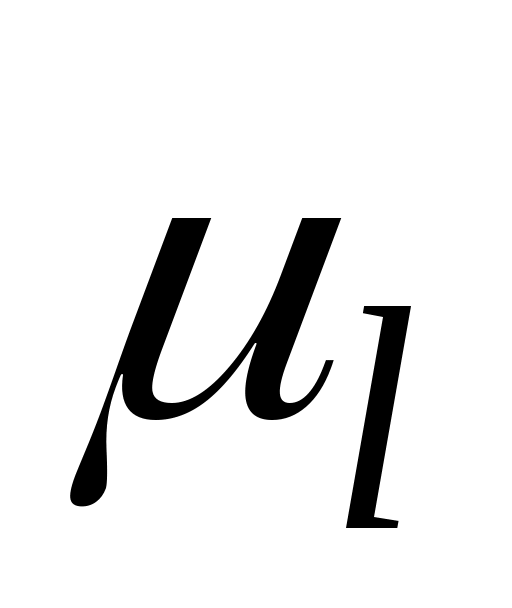 , а так как отрезки
, а так как отрезки  пропорциональны
пропорциональны 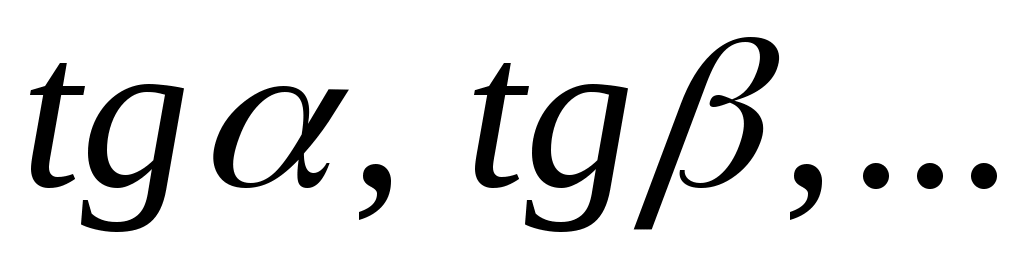 , то
, то 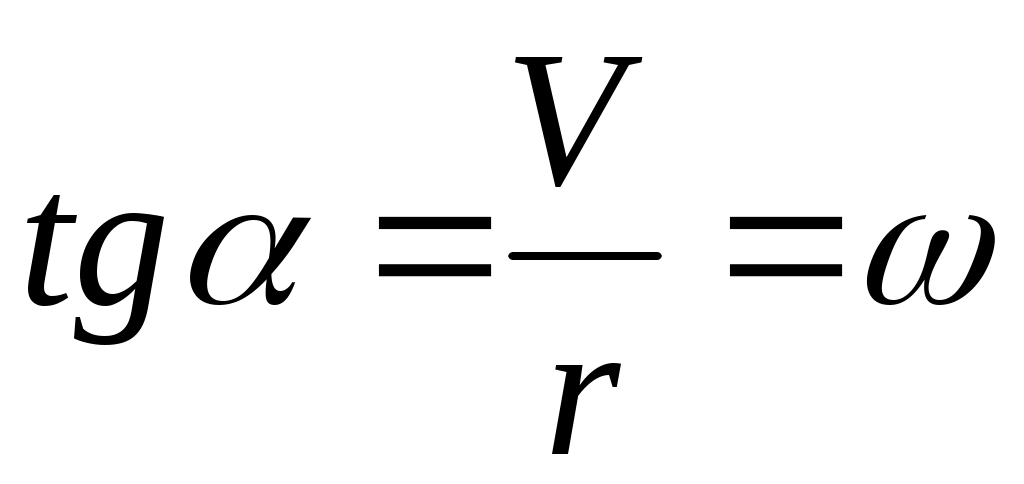 . Выбор полюсного расстояния
. Выбор полюсного расстояния 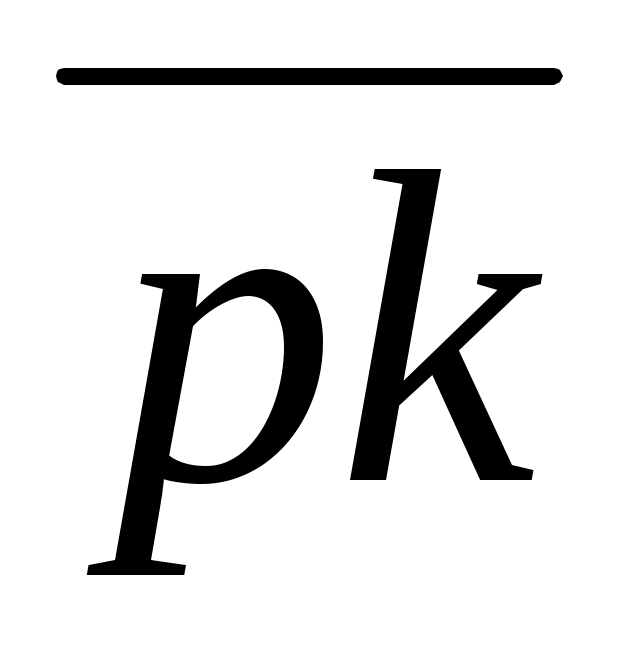 может быть произвольным.
может быть произвольным.
8.16.1. Кинематический анализ эпициклических механизмов
Простейший эпициклический механизм (редуктор Джемса) состоит из центральных колёс 1 и 3 (рис. 88), сателлитного колеса 2 и водила Н. Если одно из центральных колёс, например, колесо 3 остановить с помощью тормоза Т, то эпициклический механизм превращается в планетарный, где при вращении колеса 1 колесо 2 обегает неподвижное колесо 3, вращая водило Н с угловой скоростью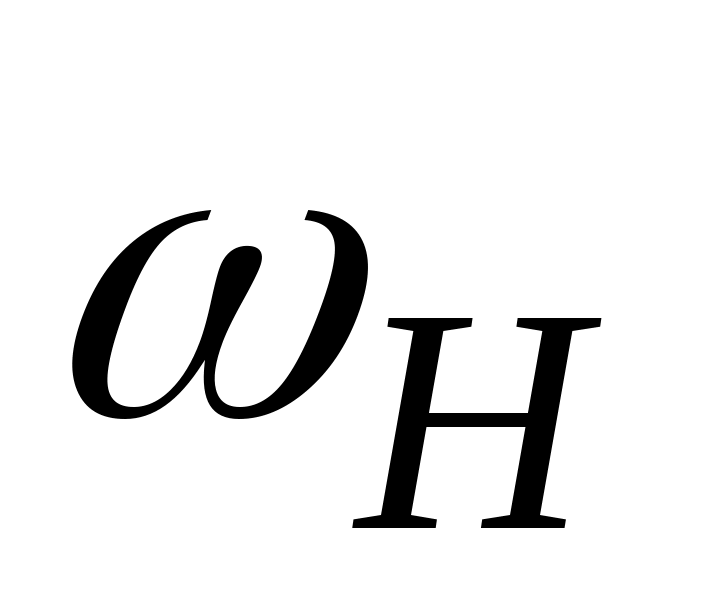 . Степень подвижности такого редуктора равна единице.
. Степень подвижности такого редуктора равна единице.
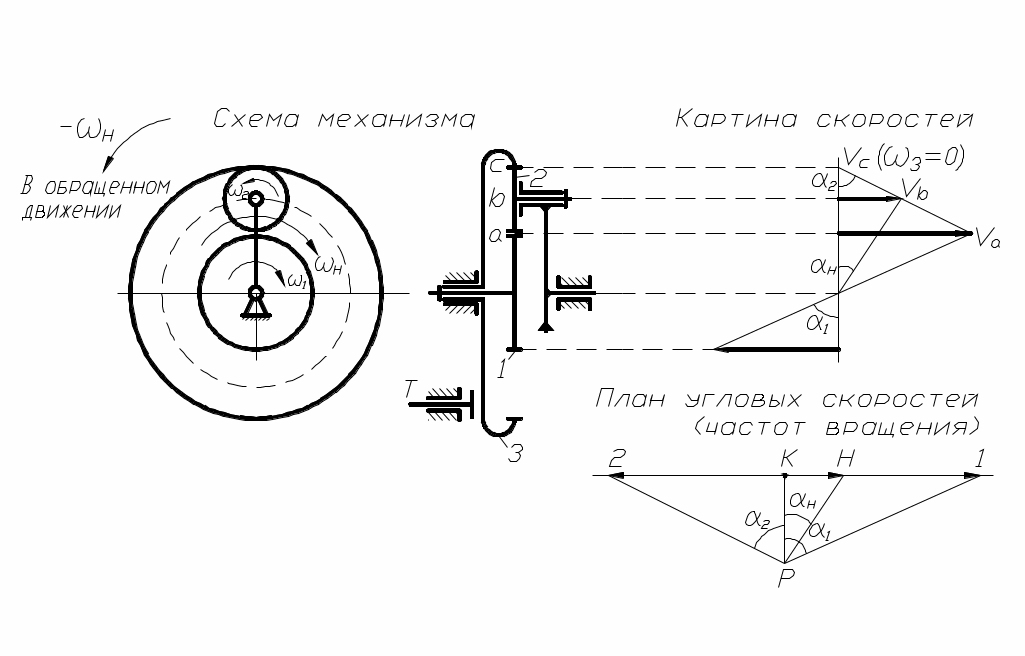
рис. 88
Для планетарного механизма можно построить картину скоростей и план угловых скоростей (частот вращения), используя рассмотренные выше приёмы (рис. 88). План угловых скоростей можно использовать для приближённого определения передаточного числа планетарного механизма, которое равно
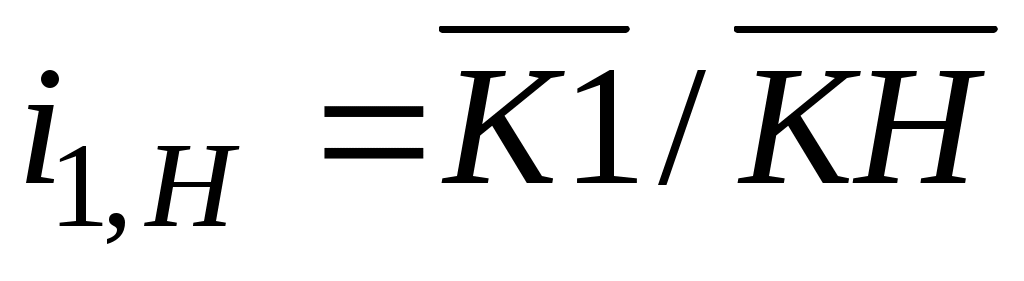 .
.
Аналитически передаточное число определяется с использованием метода обращения движения, когда механизму в целом сообщается вращение с угловой скоростью обратной скорости водила (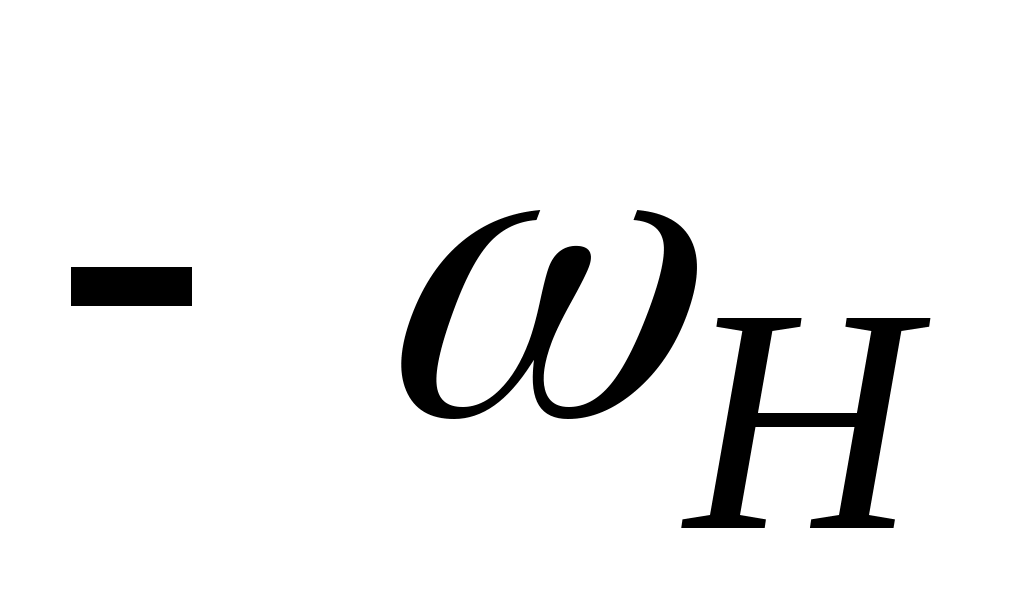 ). При этом относительное движение звеньев не изменится, а водило Н в обращённом движении будет оставаться неподвижным и планетарный редуктор превращается в рядовой (с неподвижными осями). Если обозначить угловые скорости звеньев в обращённом движении с индексом в круглых скобках указывающим неподвижное звено
). При этом относительное движение звеньев не изменится, а водило Н в обращённом движении будет оставаться неподвижным и планетарный редуктор превращается в рядовой (с неподвижными осями). Если обозначить угловые скорости звеньев в обращённом движении с индексом в круглых скобках указывающим неподвижное звено
, то
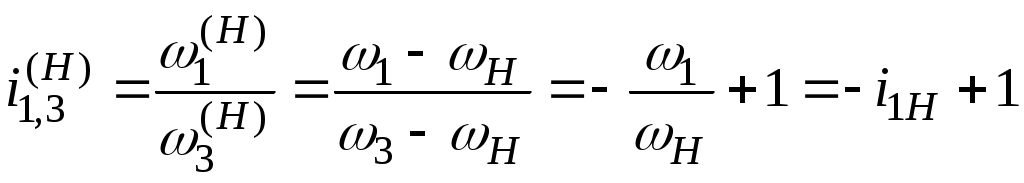 .
.
С другой стороны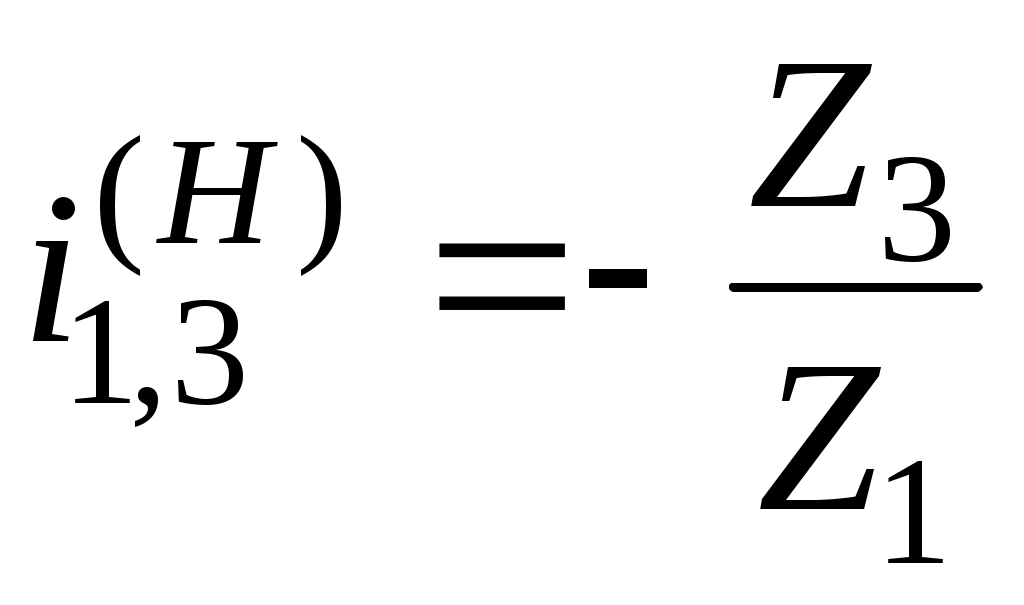 , т.е.
, т.е. 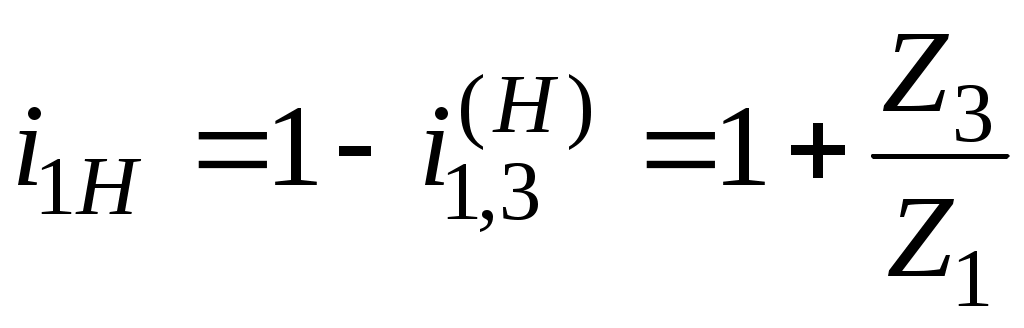 .
.
Если в эпициклическом механизме (рис. 88) оба центральных колеса совершают вращение, то степень подвижности такого механизма будет равна двум и он превращается в дифференциальный. Такие механизмы служат:
1) для привода одного рабочего органа от двух или более двигателей (т.е. для сложения движения нескольких ведущих звеньев);
2) для разложения движения одного вала на два и более независимых движений ведомых валов.
Определение угловых скоростей звеньев можно производить, пользуясь формулой Виллиса, которая позволяет получить любую неизвестную угловую скорость при заданных остальных скоростях. Эта формула записывается аналогично выведенной ранее для планетарного механизма, т.е.
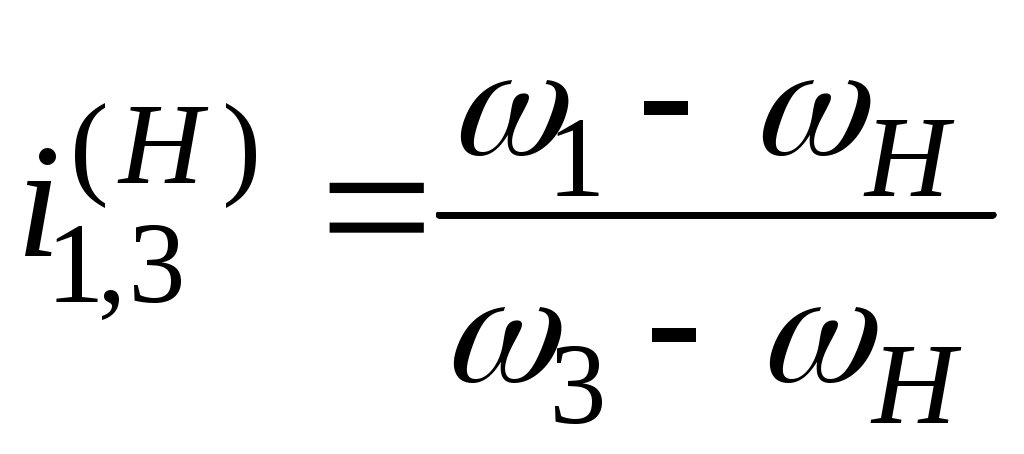 .
.
О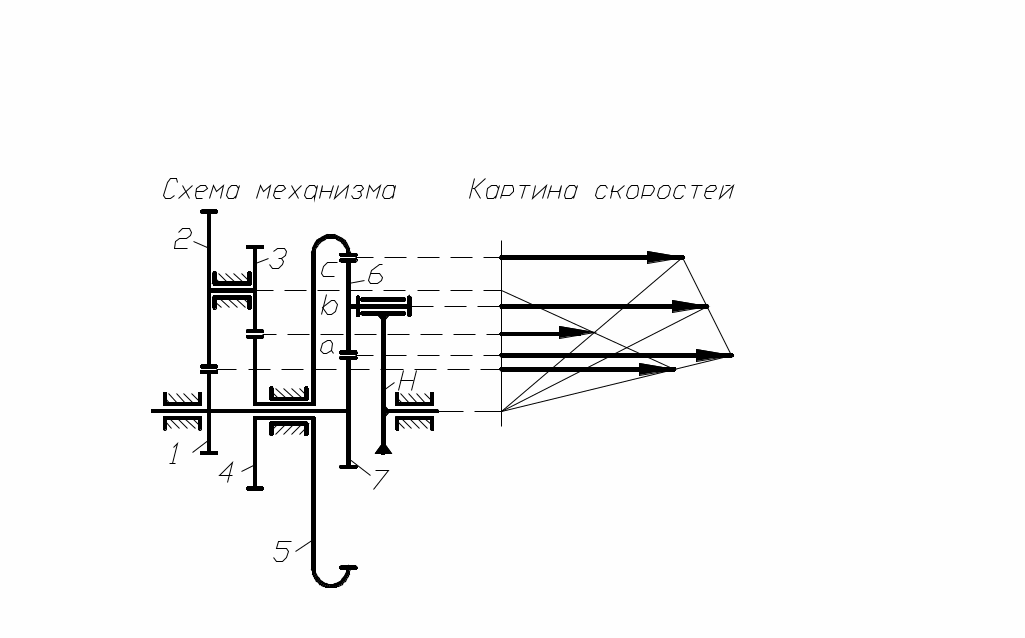 дним из распространённых типов дифференциальных механизмов являются так называемые замкнутые, в которых благодаря дополнительной зубчатой передаче связаны оба центральных колеса (рис. 89). Это позволяет использовать один двигатель для привода механизма. Для определения передаточного
дним из распространённых типов дифференциальных механизмов являются так называемые замкнутые, в которых благодаря дополнительной зубчатой передаче связаны оба центральных колеса (рис. 89). Это позволяет использовать один двигатель для привода механизма. Для определения передаточного
рис.89 отношения используем формулу
Виллиса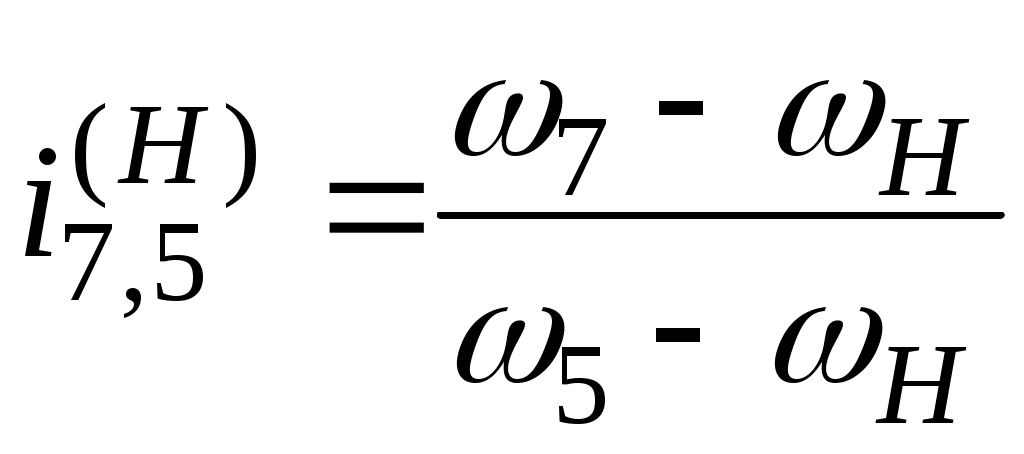 .
.
Так как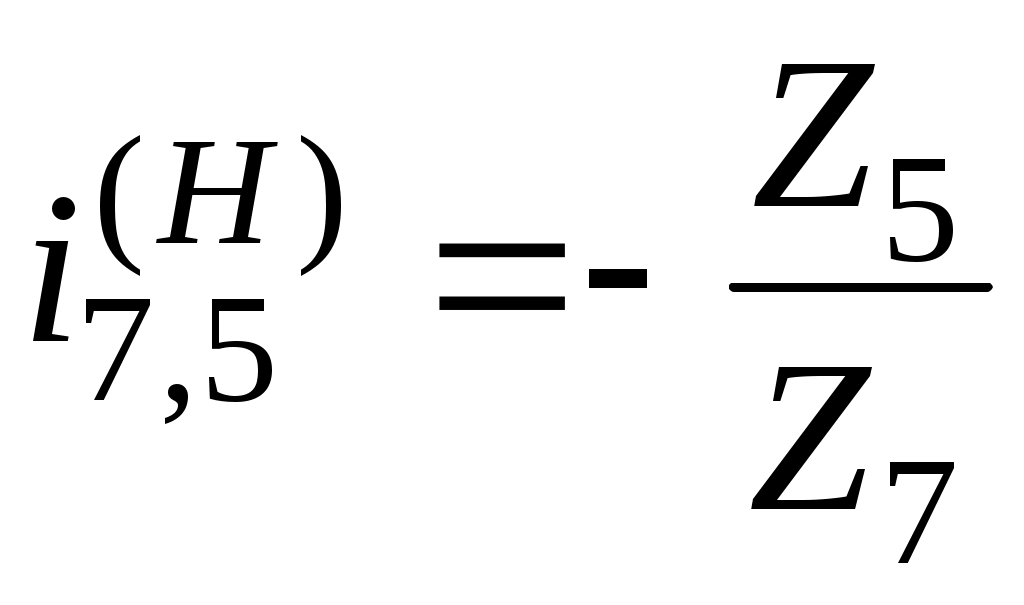 , то
, то 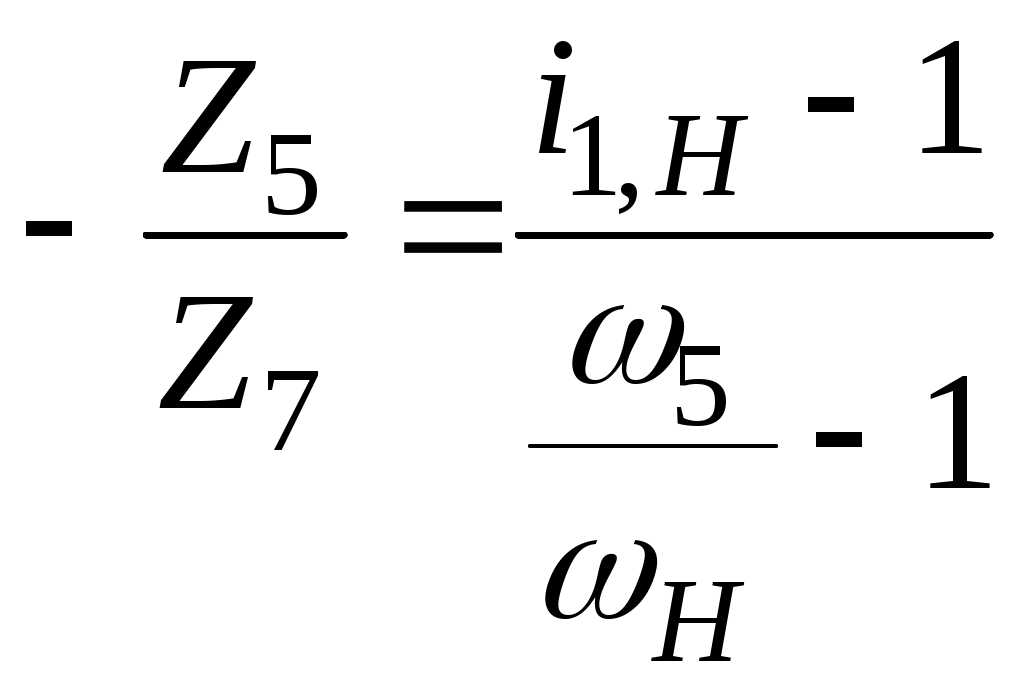 , где
, где
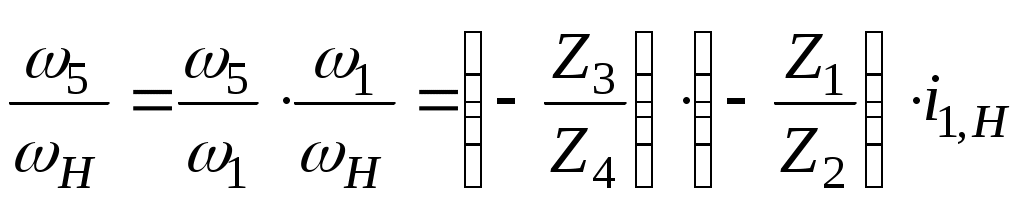 , т.е.
, т.е. 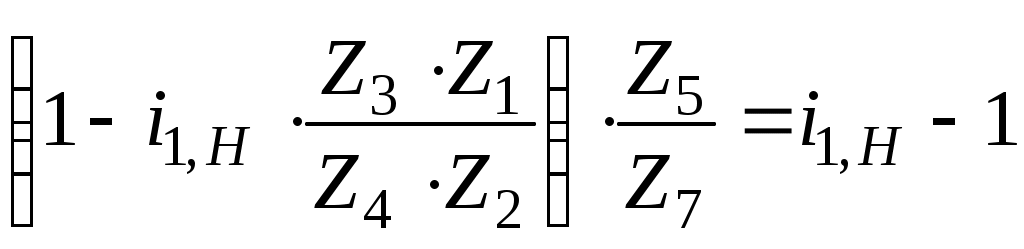 .
.
Отсюда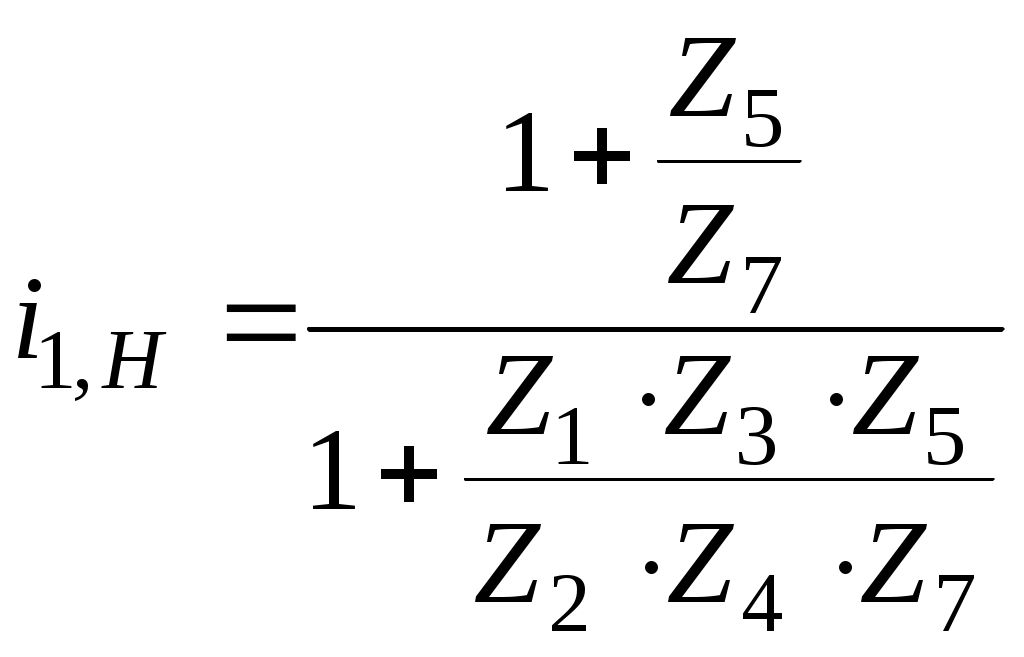 .
.
8.16.2. Эпициклические механизмы с коническими колёсами
П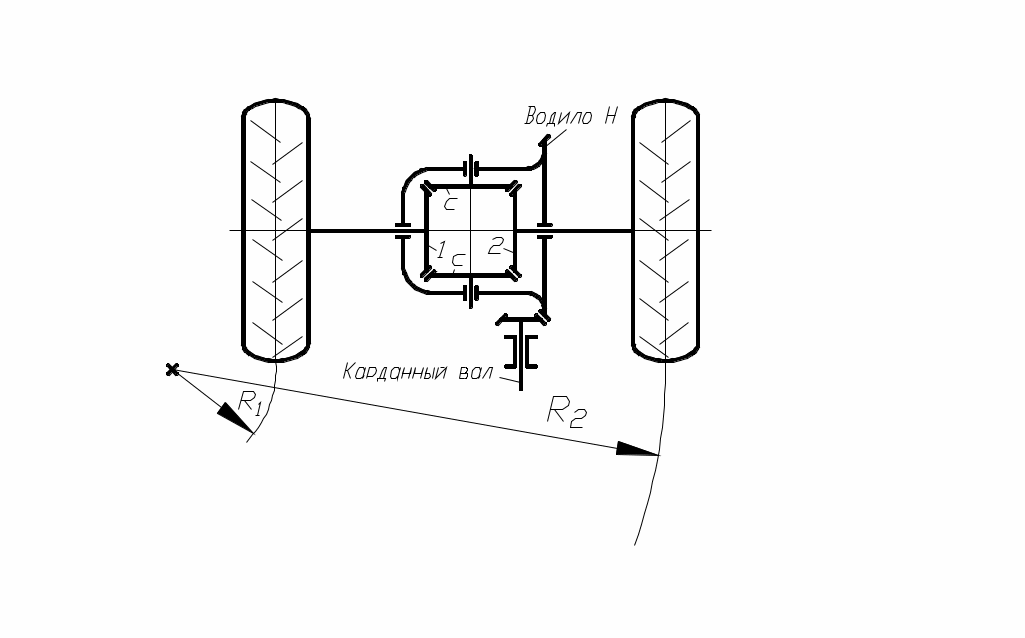 римером дифференциального механизма с коническими колёсами является дифференциал автомобиля (рис. 90). Согласно формуле Виллиса
римером дифференциального механизма с коническими колёсами является дифференциал автомобиля (рис. 90). Согласно формуле Виллиса
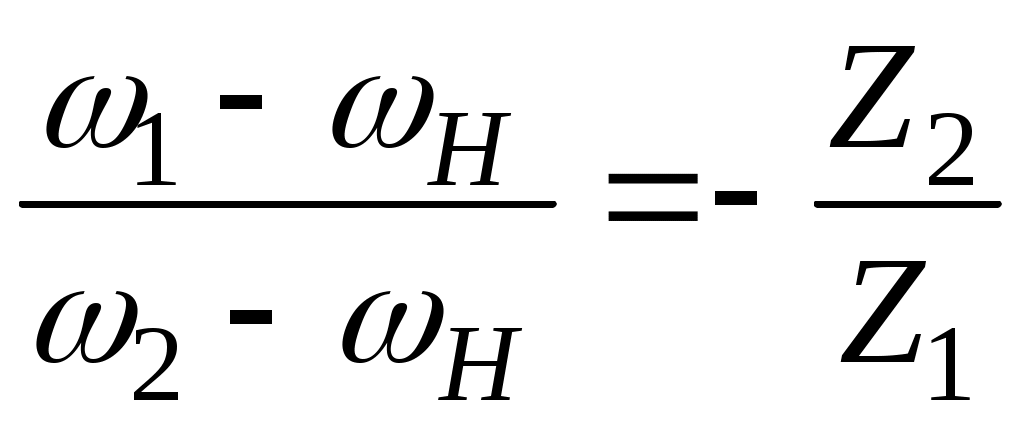 .
.
При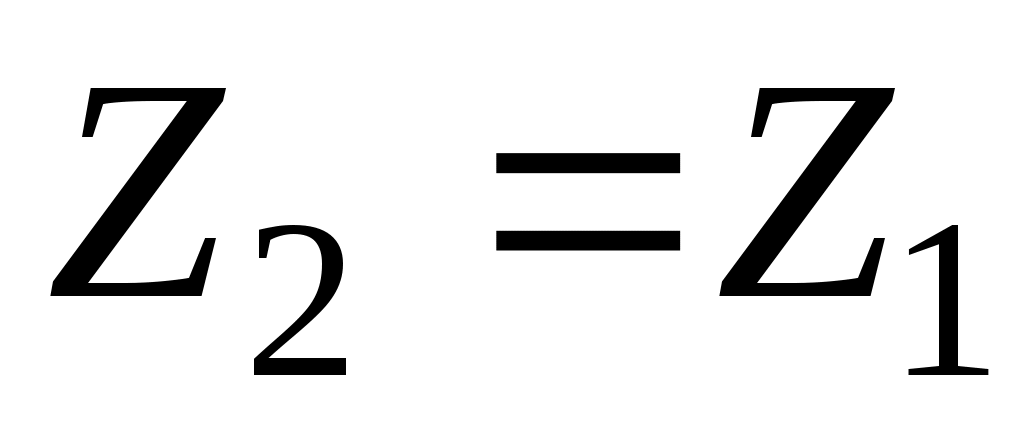 получим
получим
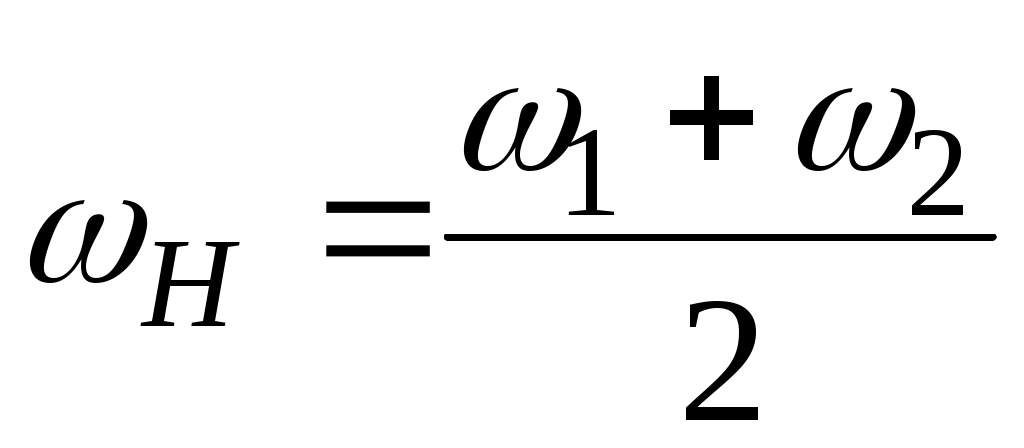 ,
,
т.е. при постоянной скорости вращения карданного вала и скорости автомобиля в целом полуоси могут вращаться с различ-
рис. 90 ными или с одинаковыми скоростями. Например, на повороте скорости вращения полуосей пропорциональны радиусам поворота R1 и R2, а при ровной прямой дороге скорость полуосей одинакова и равна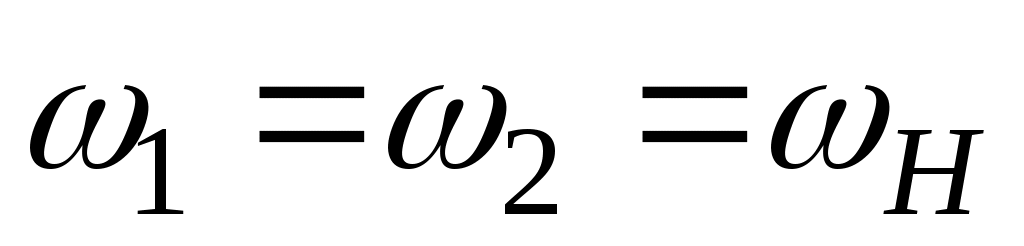 .
.
8.17. Некоторые вопросы синтеза зубчатых механизмов
Комплексные задачи синтеза зубчатых механизмов настолько сложны, что в полной постановке с учётом факторов кинематики и динамики они не решены до настоящего времени. Известны решения частных задач как геометрического, так и динамического синтеза зубчатых механизмов, причём эти решения часто носят характер рекомендаций по выбору параметров. Например, выбор передаточных отношений каждой ступени в многоступенчатом зубчатом механизме, где требуемое общее передаточное отношение равно

рекомендуется осуществлять так, чтобы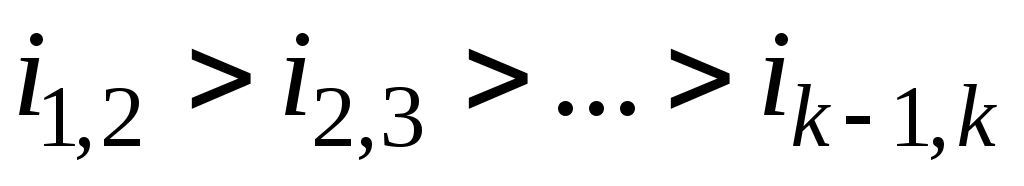 . Это связано с возрастанием нагрузки по мере уменьшения угловой скорости. Указанное распределение передаточных отношений позволяет более равномерно распределить эту нагрузку между зубчатыми колёсами.
. Это связано с возрастанием нагрузки по мере уменьшения угловой скорости. Указанное распределение передаточных отношений позволяет более равномерно распределить эту нагрузку между зубчатыми колёсами.
При заданных передаточных отношениях и известном числе зубьев колёс задача синтеза сводится к определению их параметров. При этом сначала выбирается материал колёс с учётом назначения передачи, условий работы и других факторов, затем определяется модуль передачи, позволяющий обеспечить
изгибную и контактную прочность зубьев, а затем – все геометрические параметры зубчатых колёс.
Известны решения частных задач подбора чисел зубьев сложных зубчатых механизмов с учётом различных условий, например, геометрического характера.
8.17.1. Синтез эпициклических механизмов с цилиндрическими
колёсами. Условия синтеза
При проектировании планетарного редуктора с заданным передаточным отношением возникает задача определения чисел зубьев при соблюдении следующих условий:
1) кинематическое условие;
2) условие соосности;
3) условие соседства;
4) условие сборки;
5) условие правильного зацепления.
Физический и математический смысл этих условий разберём на конкретной схеме планетарного механизма с нулевыми эвольвентными цилиндрическими колёсами (рис. 91).
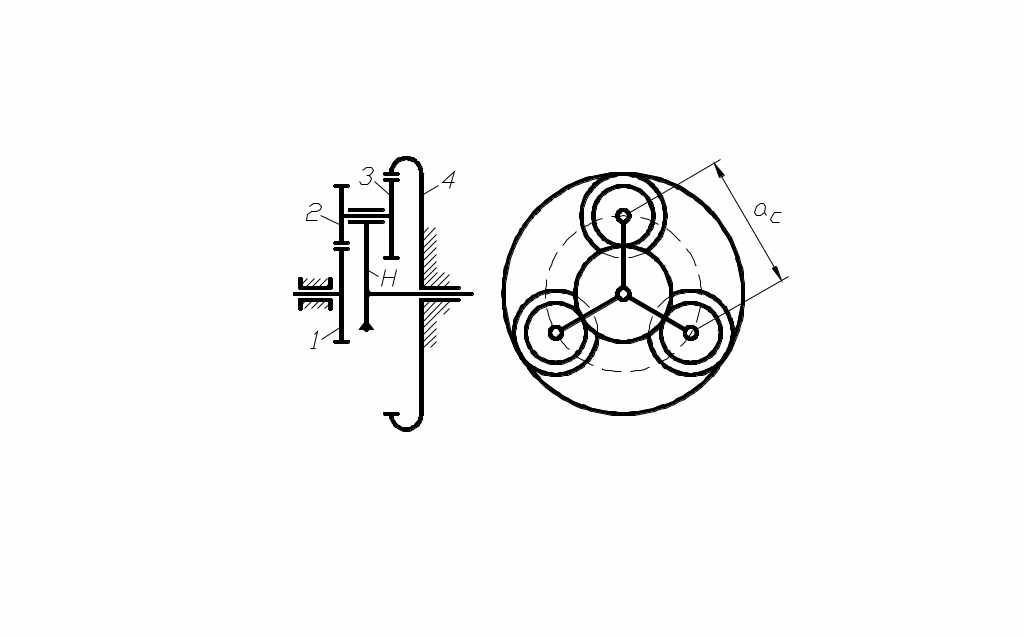 Кинематическое условие обеспечивает заданное передаточное отношение и для данного механизма имеет следующий вид:
Кинематическое условие обеспечивает заданное передаточное отношение и для данного механизма имеет следующий вид:
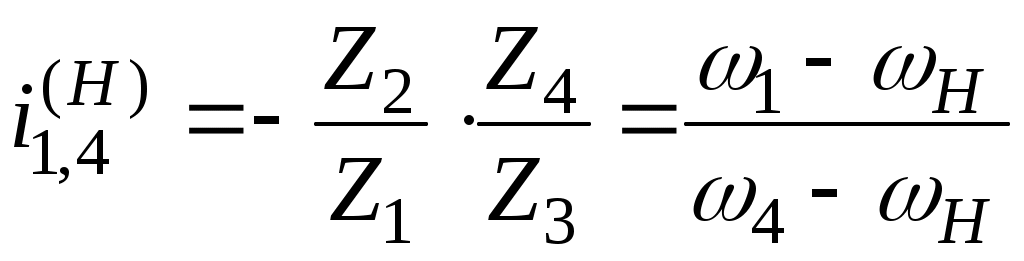
или при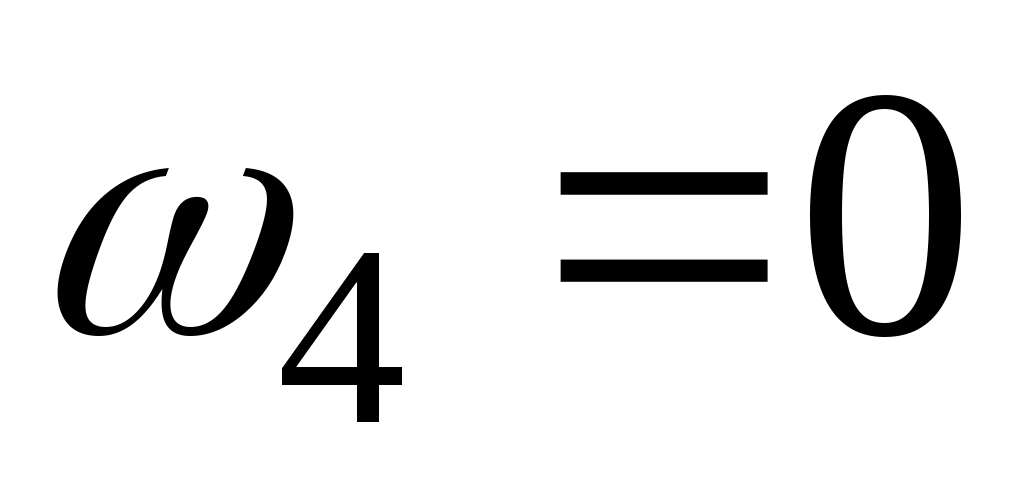 получим
получим
рис. 91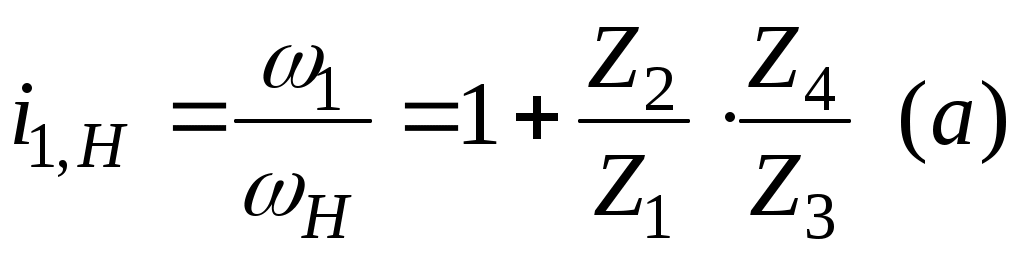 .
.
Обычно допускается отклонение передаточного отношения в пределах 5% от заданного.
Условие соосности требует, чтобы оси колёс 1 и 4, в данном случае, совпадали для обеспечения зацепления сателлитов с центральными колёсами. Для этого необходимо, чтобы выполнялось соотношение радиусов делительных окружностей
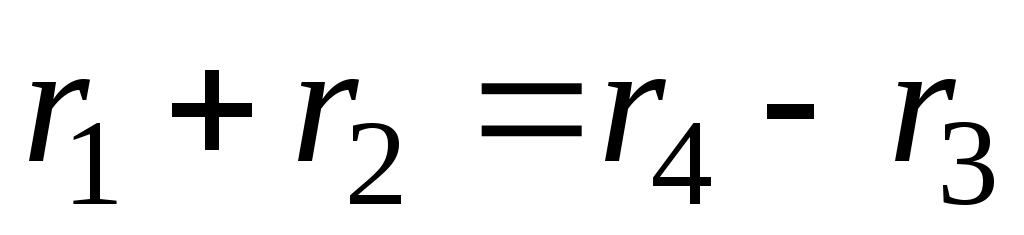 ,
,
а при одинаковых модулях всех колёс: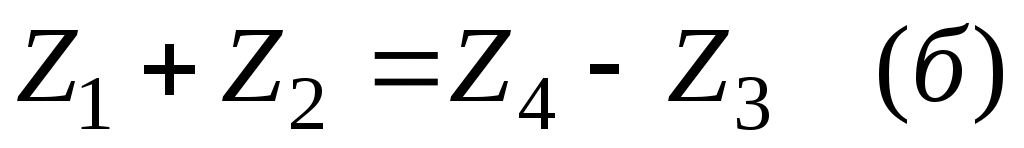 .
.
Условие соседства включает требование совместного размещения нескольких сателлитов по общей окружности так, чтобы они не задевали друг друга своими зубьями. Необходимость выполнения этого условия возникает при числе сателлитов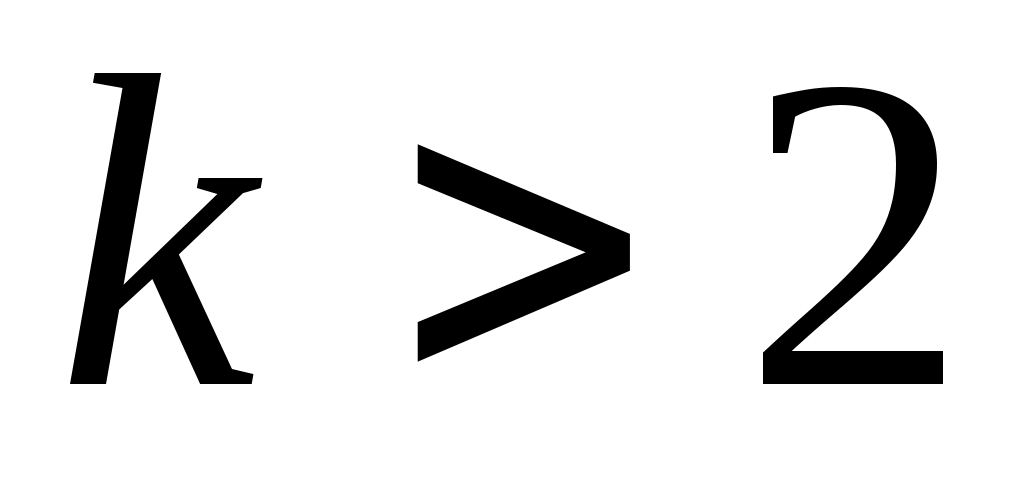 (увеличение числа сателлитов уменьшает нагрузку на зубья). В этом случае необходимо, чтобы
(увеличение числа сателлитов уменьшает нагрузку на зубья). В этом случае необходимо, чтобы 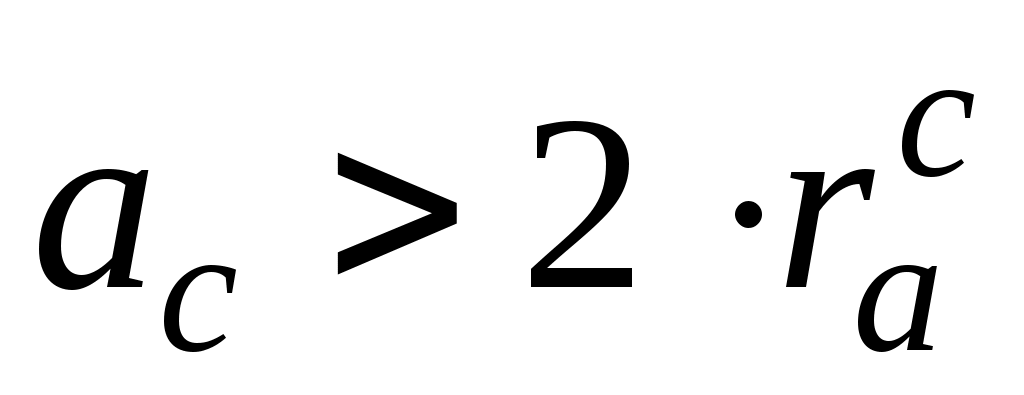
(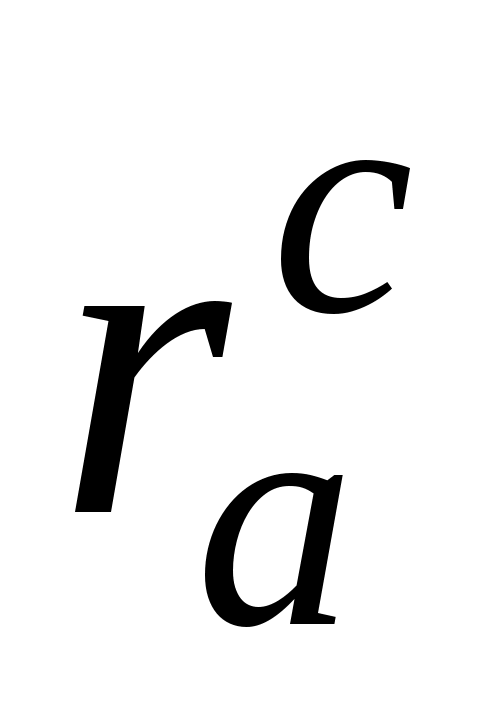 - радиус окружности вершин наибольшего сателлита). Так как
- радиус окружности вершин наибольшего сателлита). Так как
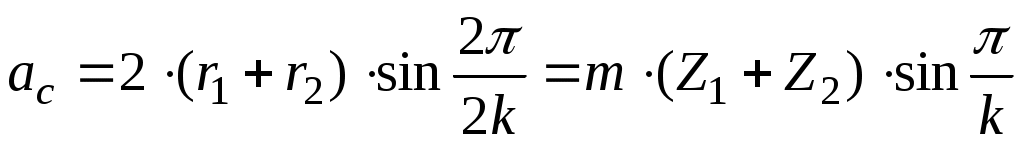 ;
;
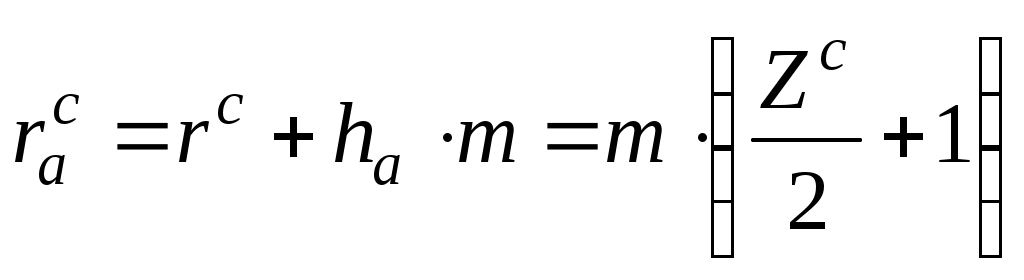 ,
,
то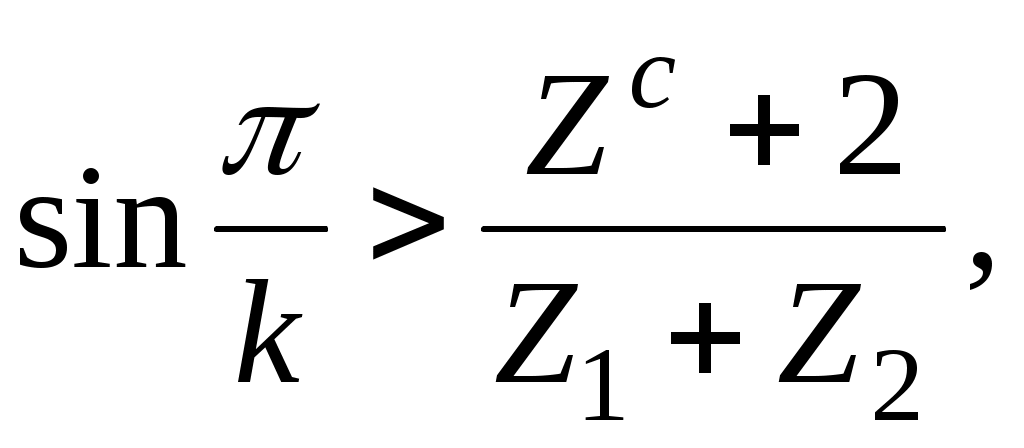 (в)
(в)
где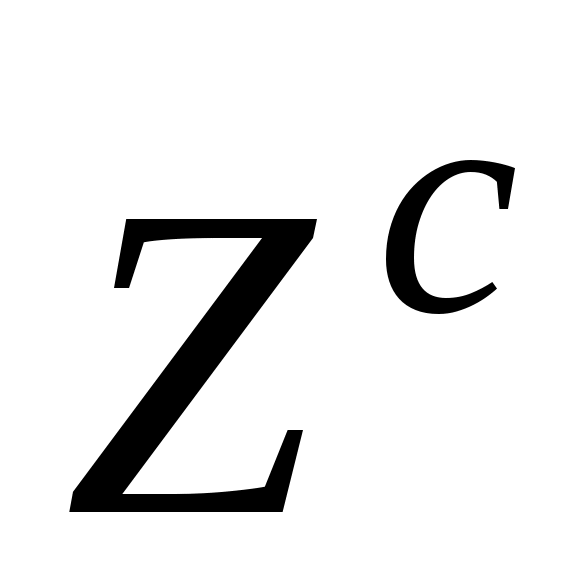 - число зубьев наибольшего сателлита (2 или 3).
- число зубьев наибольшего сателлита (2 или 3).
Условие сборки учитывает необходимость одновременного зацепления всех сателлитов с центральными колёсами, т.е. установив первый сателлит и повернув водило на угол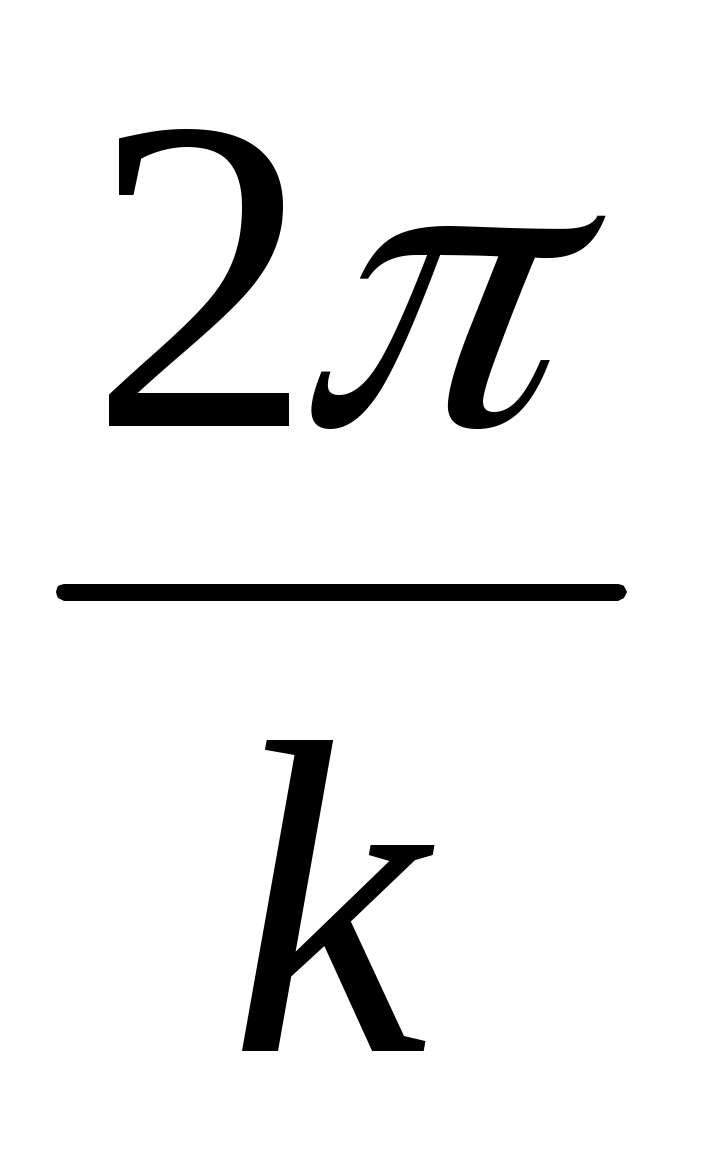 рад., необходимо в то же самое место установить следующий сателлит. Это может быть осуществлено, если зубья колёс второго блока сателлитов окажутся точно против впадин зубьев центральных колёс. Иначе сборку осуществить невозможно. Для формирования условия примем, что оба колеса всех
рад., необходимо в то же самое место установить следующий сателлит. Это может быть осуществлено, если зубья колёс второго блока сателлитов окажутся точно против впадин зубьев центральных колёс. Иначе сборку осуществить невозможно. Для формирования условия примем, что оба колеса всех 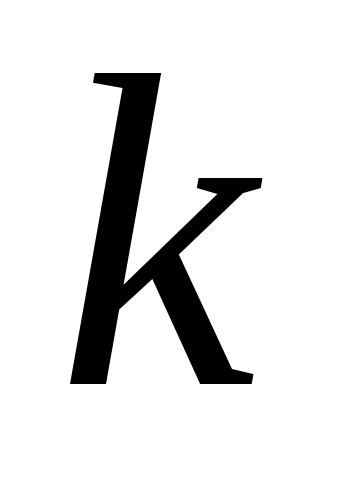 блоков сателлитов имеют одинаковую ориентацию зубьев друг относительно друга. После установки первого сателлита на ось водило должно быть повёрнуто на угол
блоков сателлитов имеют одинаковую ориентацию зубьев друг относительно друга. После установки первого сателлита на ось водило должно быть повёрнуто на угол 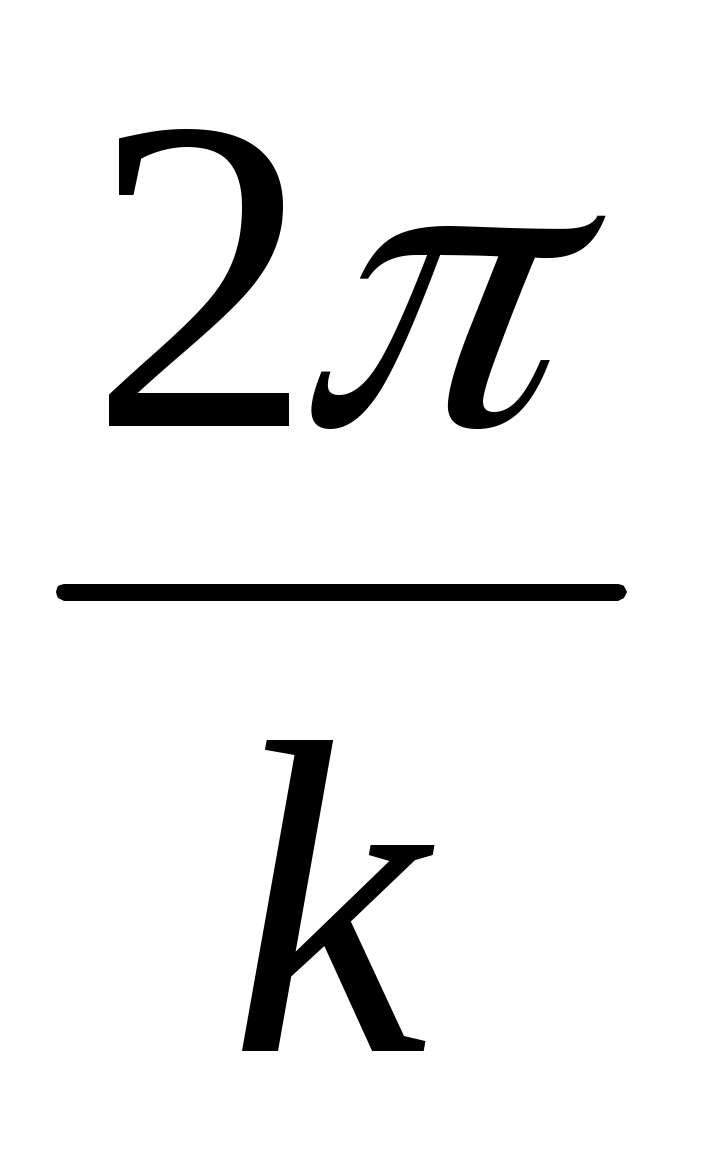 рад., при этом колесо 1 необходимо повернуть на угол
рад., при этом колесо 1 необходимо повернуть на угол 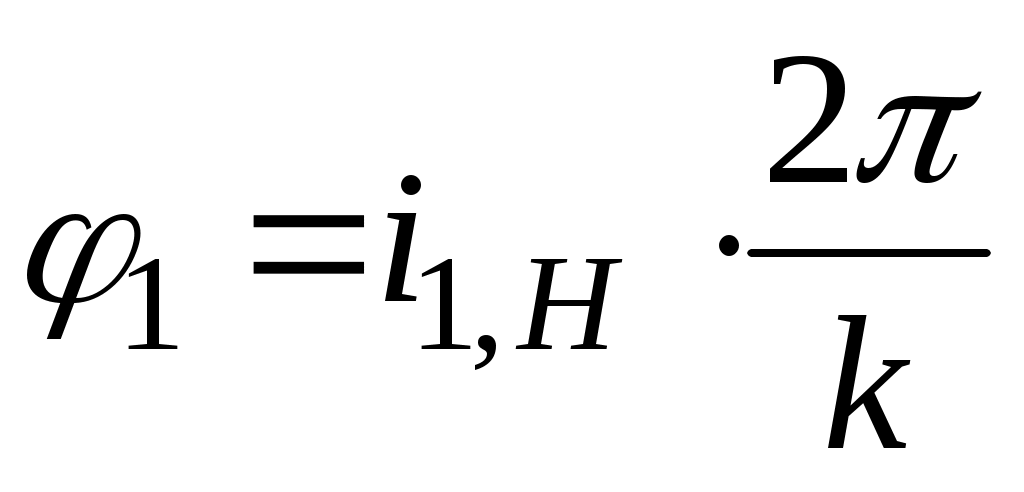 рад. С другой стороны угол поворота колеса 1 (
рад. С другой стороны угол поворота колеса 1 (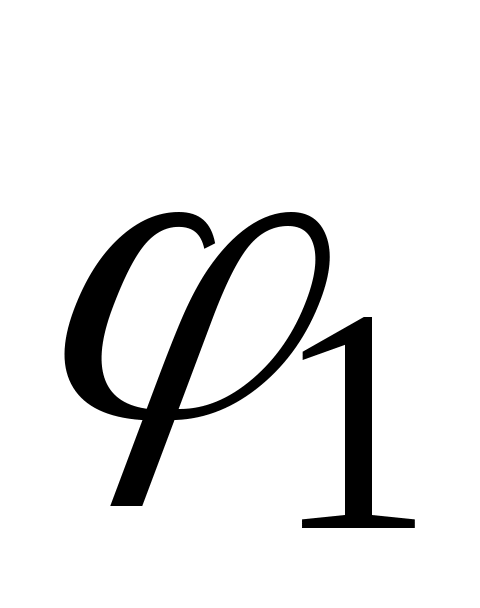 ) должен быть кратным его угловому шагу зубьев
) должен быть кратным его угловому шагу зубьев 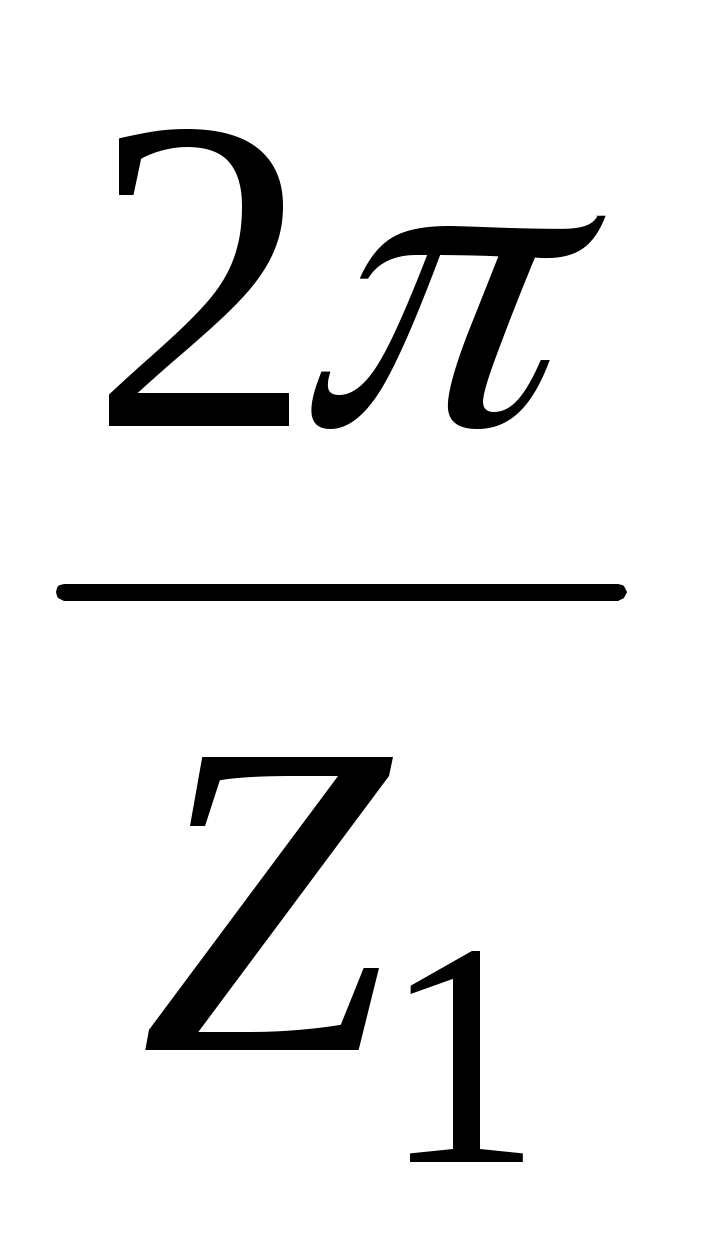 , в противном случае при повороте на угол
, в противном случае при повороте на угол 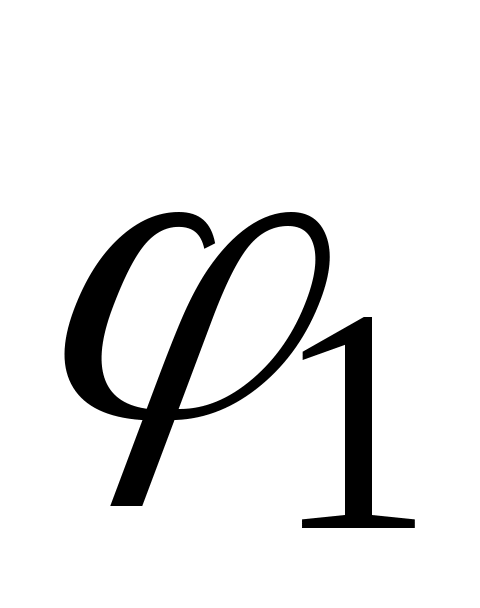 положение зубьев колеса 1 изменится и второй сателлит вставить будет невозможно. Таким образом
положение зубьев колеса 1 изменится и второй сателлит вставить будет невозможно. Таким образом 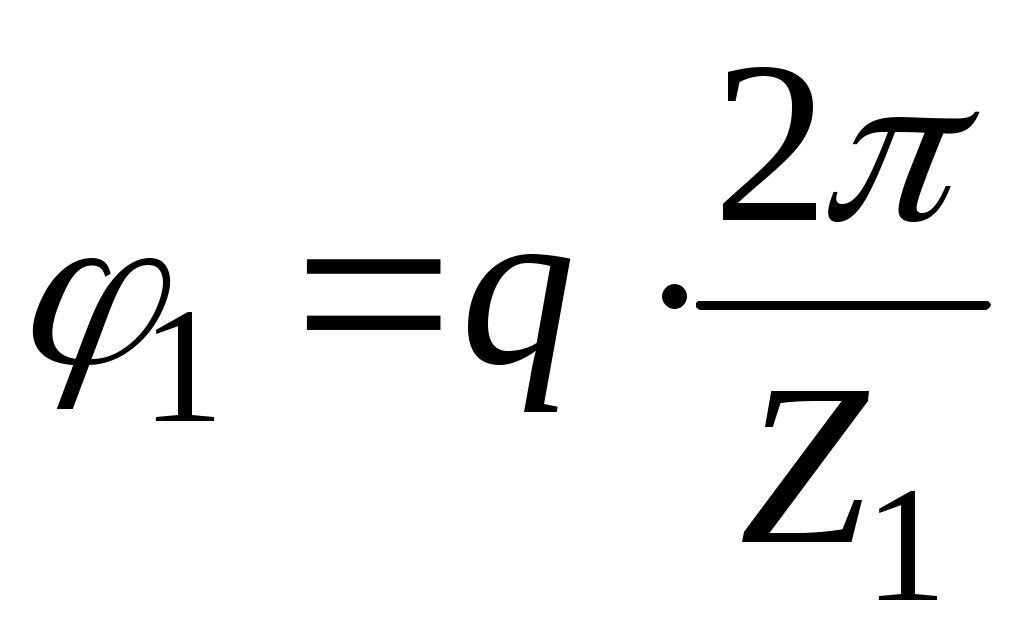 (q – целое число) и
(q – целое число) и
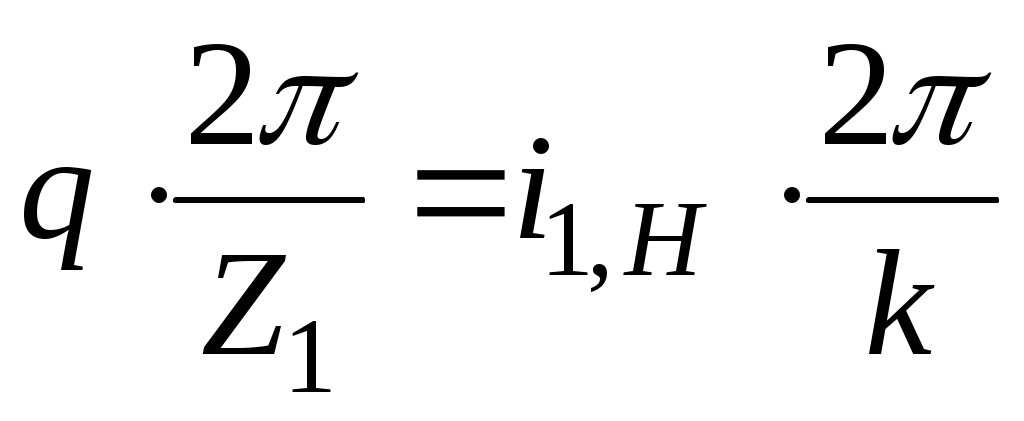 или
или 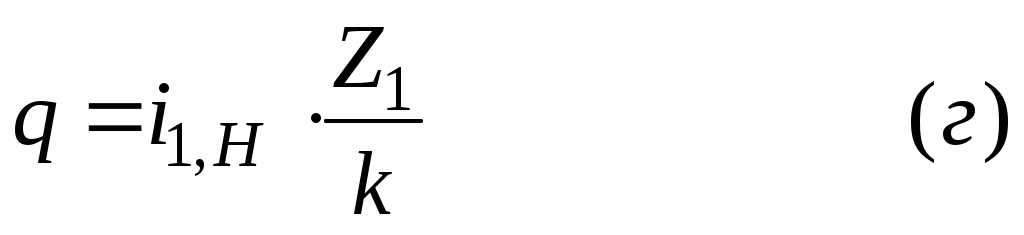
Условие правильного зацепления
8.16.1. Кинематический анализ эпициклических механизмов
Простейший эпициклический механизм (редуктор Джемса) состоит из центральных колёс 1 и 3 (рис. 88), сателлитного колеса 2 и водила Н. Если одно из центральных колёс, например, колесо 3 остановить с помощью тормоза Т, то эпициклический механизм превращается в планетарный, где при вращении колеса 1 колесо 2 обегает неподвижное колесо 3, вращая водило Н с угловой скоростью

рис. 88
Для планетарного механизма можно построить картину скоростей и план угловых скоростей (частот вращения), используя рассмотренные выше приёмы (рис. 88). План угловых скоростей можно использовать для приближённого определения передаточного числа планетарного механизма, которое равно
Аналитически передаточное число определяется с использованием метода обращения движения, когда механизму в целом сообщается вращение с угловой скоростью обратной скорости водила (
, то
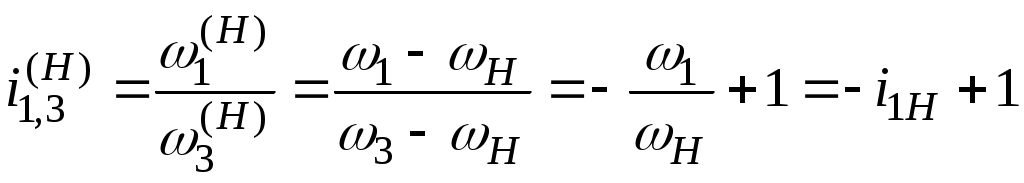 .
.С другой стороны
Если в эпициклическом механизме (рис. 88) оба центральных колеса совершают вращение, то степень подвижности такого механизма будет равна двум и он превращается в дифференциальный. Такие механизмы служат:
1) для привода одного рабочего органа от двух или более двигателей (т.е. для сложения движения нескольких ведущих звеньев);
2) для разложения движения одного вала на два и более независимых движений ведомых валов.
Определение угловых скоростей звеньев можно производить, пользуясь формулой Виллиса, которая позволяет получить любую неизвестную угловую скорость при заданных остальных скоростях. Эта формула записывается аналогично выведенной ранее для планетарного механизма, т.е.
О
 дним из распространённых типов дифференциальных механизмов являются так называемые замкнутые, в которых благодаря дополнительной зубчатой передаче связаны оба центральных колеса (рис. 89). Это позволяет использовать один двигатель для привода механизма. Для определения передаточного
дним из распространённых типов дифференциальных механизмов являются так называемые замкнутые, в которых благодаря дополнительной зубчатой передаче связаны оба центральных колеса (рис. 89). Это позволяет использовать один двигатель для привода механизма. Для определения передаточного рис.89 отношения используем формулу
Виллиса
Так как
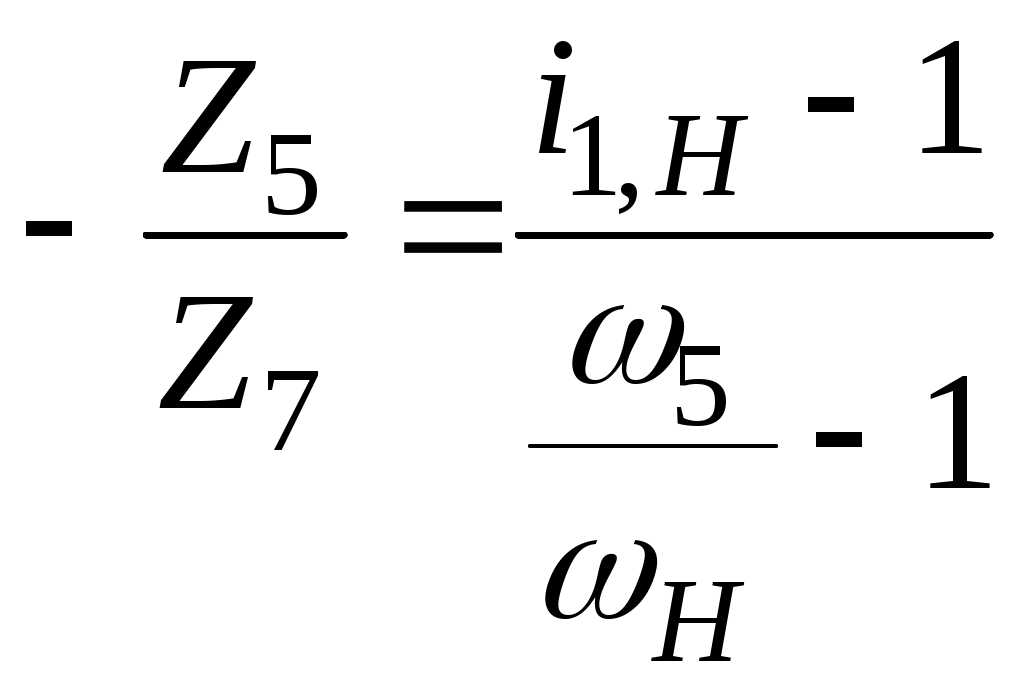 , где
, гдеОтсюда
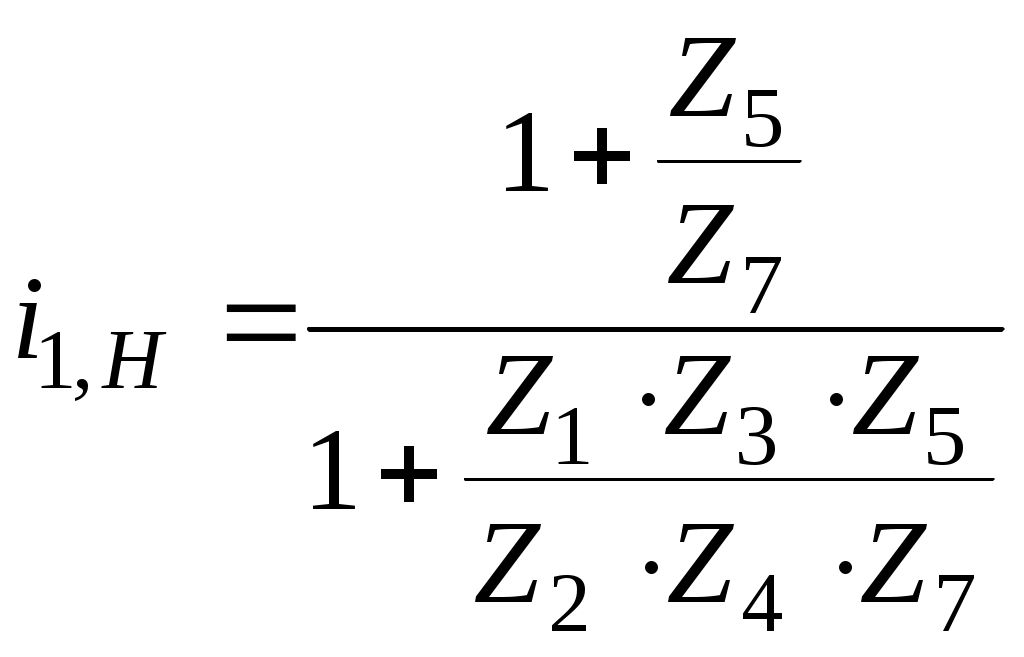 .
.
8.16.2. Эпициклические механизмы с коническими колёсами
П
 римером дифференциального механизма с коническими колёсами является дифференциал автомобиля (рис. 90). Согласно формуле Виллиса
римером дифференциального механизма с коническими колёсами является дифференциал автомобиля (рис. 90). Согласно формуле ВиллисаПри
т.е. при постоянной скорости вращения карданного вала и скорости автомобиля в целом полуоси могут вращаться с различ-
рис. 90 ными или с одинаковыми скоростями. Например, на повороте скорости вращения полуосей пропорциональны радиусам поворота R1 и R2, а при ровной прямой дороге скорость полуосей одинакова и равна
8.17. Некоторые вопросы синтеза зубчатых механизмов
Комплексные задачи синтеза зубчатых механизмов настолько сложны, что в полной постановке с учётом факторов кинематики и динамики они не решены до настоящего времени. Известны решения частных задач как геометрического, так и динамического синтеза зубчатых механизмов, причём эти решения часто носят характер рекомендаций по выбору параметров. Например, выбор передаточных отношений каждой ступени в многоступенчатом зубчатом механизме, где требуемое общее передаточное отношение равно
рекомендуется осуществлять так, чтобы
При заданных передаточных отношениях и известном числе зубьев колёс задача синтеза сводится к определению их параметров. При этом сначала выбирается материал колёс с учётом назначения передачи, условий работы и других факторов, затем определяется модуль передачи, позволяющий обеспечить
изгибную и контактную прочность зубьев, а затем – все геометрические параметры зубчатых колёс.
Известны решения частных задач подбора чисел зубьев сложных зубчатых механизмов с учётом различных условий, например, геометрического характера.
8.17.1. Синтез эпициклических механизмов с цилиндрическими
колёсами. Условия синтеза
При проектировании планетарного редуктора с заданным передаточным отношением возникает задача определения чисел зубьев при соблюдении следующих условий:
1) кинематическое условие;
2) условие соосности;
3) условие соседства;
4) условие сборки;
5) условие правильного зацепления.
Физический и математический смысл этих условий разберём на конкретной схеме планетарного механизма с нулевыми эвольвентными цилиндрическими колёсами (рис. 91).
 Кинематическое условие обеспечивает заданное передаточное отношение и для данного механизма имеет следующий вид:
Кинематическое условие обеспечивает заданное передаточное отношение и для данного механизма имеет следующий вид:или при
рис. 91
Обычно допускается отклонение передаточного отношения в пределах 5% от заданного.
Условие соосности требует, чтобы оси колёс 1 и 4, в данном случае, совпадали для обеспечения зацепления сателлитов с центральными колёсами. Для этого необходимо, чтобы выполнялось соотношение радиусов делительных окружностей
а при одинаковых модулях всех колёс:
Условие соседства включает требование совместного размещения нескольких сателлитов по общей окружности так, чтобы они не задевали друг друга своими зубьями. Необходимость выполнения этого условия возникает при числе сателлитов
(
то
где
Условие сборки учитывает необходимость одновременного зацепления всех сателлитов с центральными колёсами, т.е. установив первый сателлит и повернув водило на угол
Условие правильного зацепления