Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 147
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
a=0). Опасность заострения наиболее велика у колёс с малым числом зубьев (Z<15). Для предотвращения разрушения заострённого зуба коэффициент смещения χ назначают с расчётом, чтобы Sa≥0,2m.
8.12. Выбор расчётных коэффициентов смещения
для передач внешнего зацепления
При назначении коэффициентов смещения χ1 и χ2 для любой передачи должны выполняться три условия:
1) отсутствие подрезания;
2) отсутствие заострения;
3) непрерывность зацепления.
П ервое условие выполняется при
ервое условие выполняется при 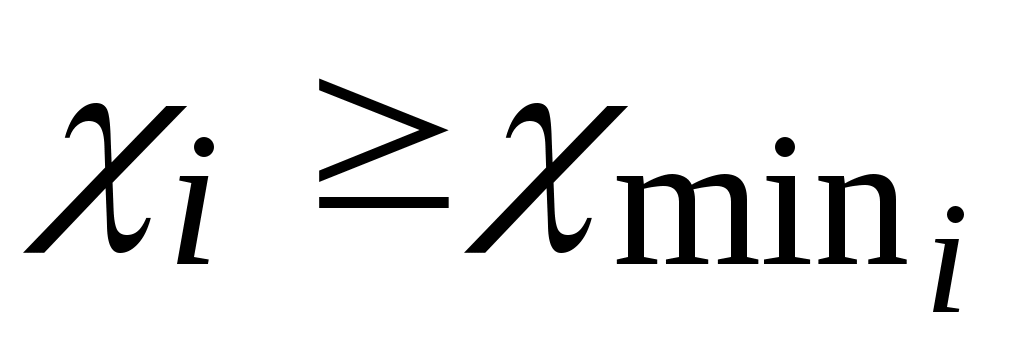 (
(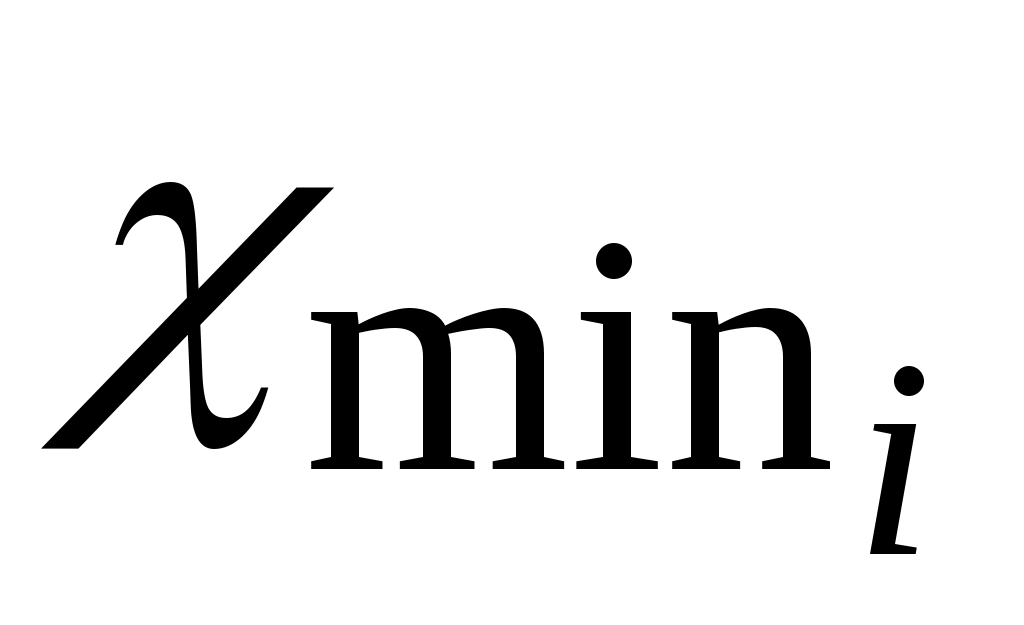 определяются из условия отсутствия подреза). Второе и третье условия выполняются при ограничении верхних пределов
определяются из условия отсутствия подреза). Второе и третье условия выполняются при ограничении верхних пределов 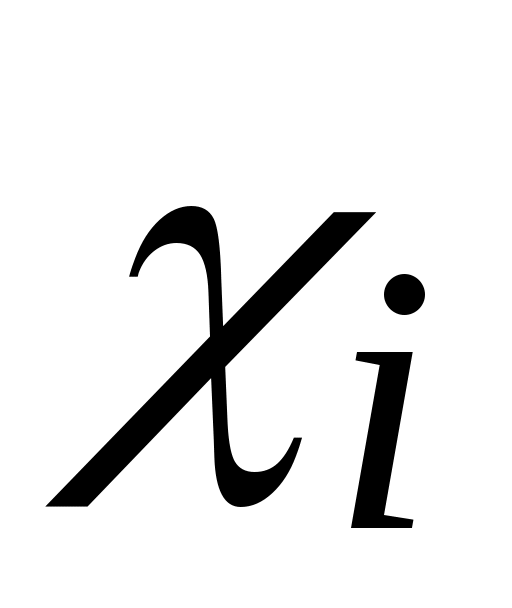 величинами
величинами 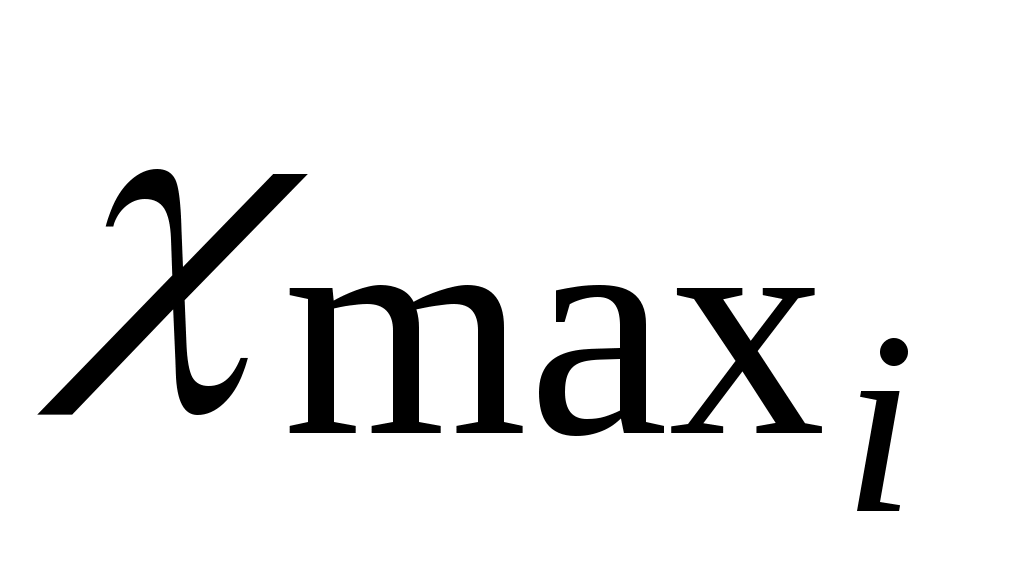 с учётом возможности заострения зубьев и уменьшения коэффициента перекрытия
с учётом возможности заострения зубьев и уменьшения коэффициента перекрытия  до величины
до величины 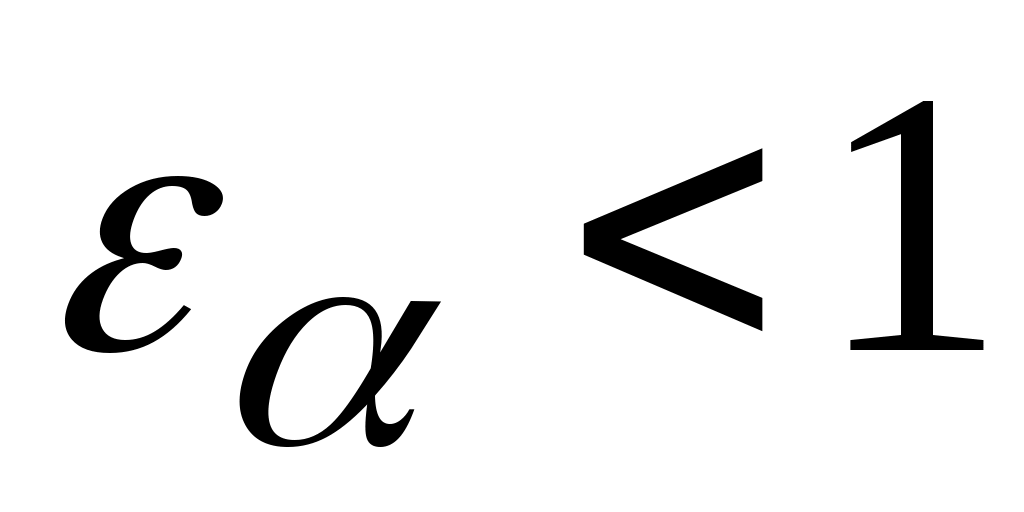 . То есть при выборе
. То есть при выборе 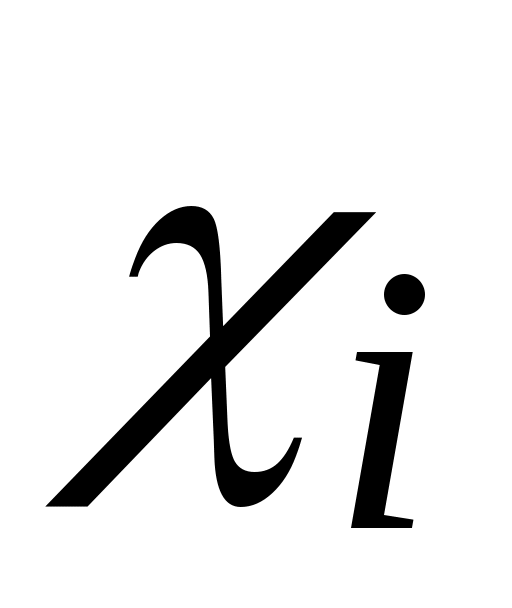 необходимо чтобы
необходимо чтобы 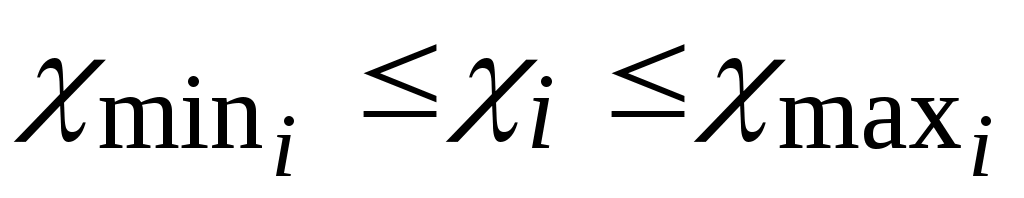 , где
, где 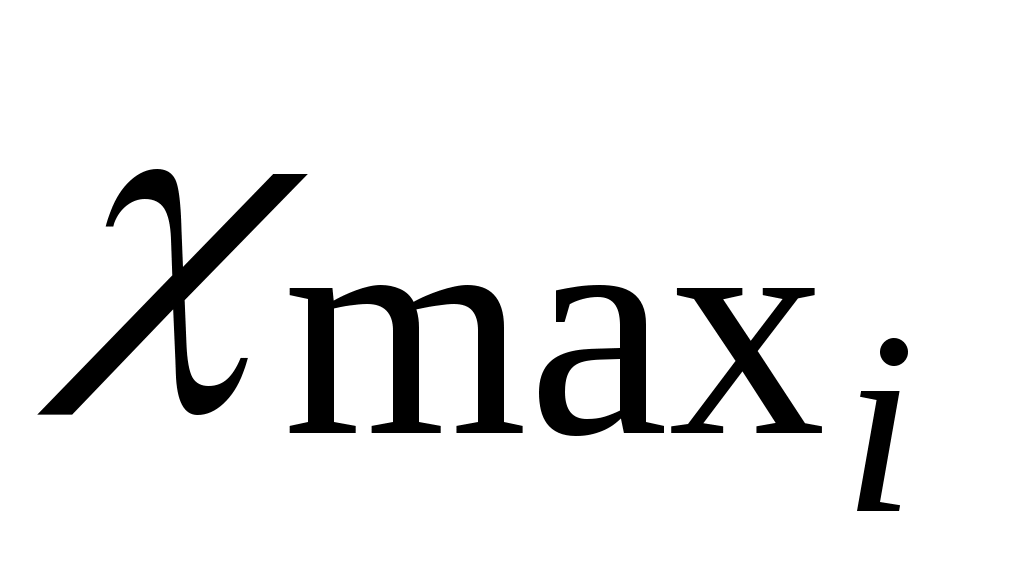 для каждого из колёс берётся наименьшим из значений, учитывающих заострение зуба и снижения
для каждого из колёс берётся наименьшим из значений, учитывающих заострение зуба и снижения  до величины
до величины 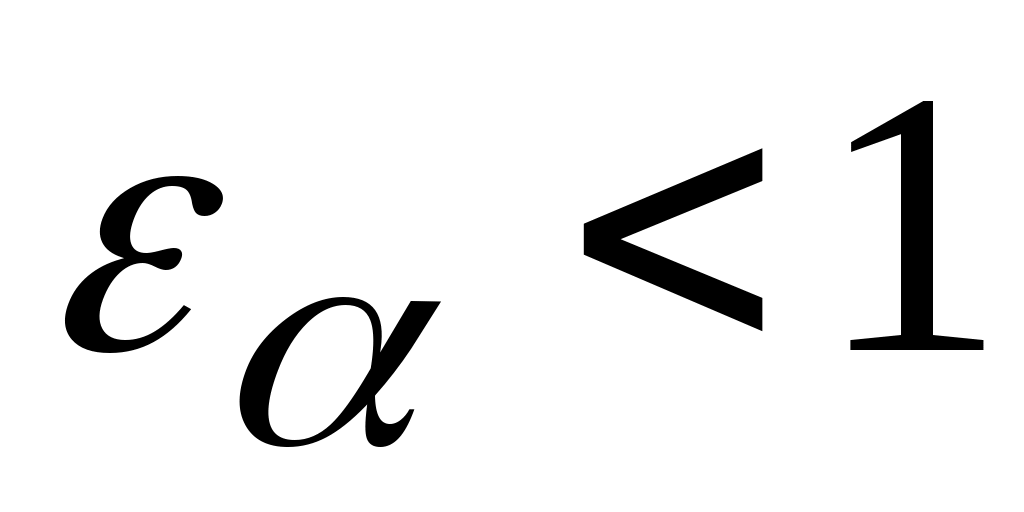 .
.
Внутри указанных диапазонов χ назначаются так, чтобы по возможности улучшить качественные показатели передачи (прочность, износостойкость, плавность хода).
Для передачи можно построить область допустимых значений коэффициентов смещения в координатах χ1 и χ2 , которая называется блокирующим контуром. Допустимые значения χ1 и χ2 расположены внутри контура (рис. 81). Для каждой передачи можно построить свой контур. Такие блокирующие контуры для различных передач имеются в справочной литера-
рис. 81 туре.
8.13. Цилиндрические колёса с косыми зубьями и их особенности
Образование косозубого колеса можно представить, если взять цилиндрическое прямозубое колесо и сообщить ему крутильную деформацию. При этом угол скручивания, образованный осью колеса и винтовой линией, является углом наклона винтовой линии βº.
Цилиндрические колёса с косыми зубьями применяются при передаче вращения между параллельными и перекрещивающимися осями. В передаче с параллельными осями углы βº обоих колёс равны по величине и противоположны по направлению при внешнем зацеплении и одинаковы по направлению при внутреннем зацеплении. Угол βº (рис. 82, а) называется углом наклона зубьев по делительному цилиндру радиуса r. С другими соосными цилиндрами, начальным (rw) и основным (rb) винтовая поверхность зуба образует, соответственно, углы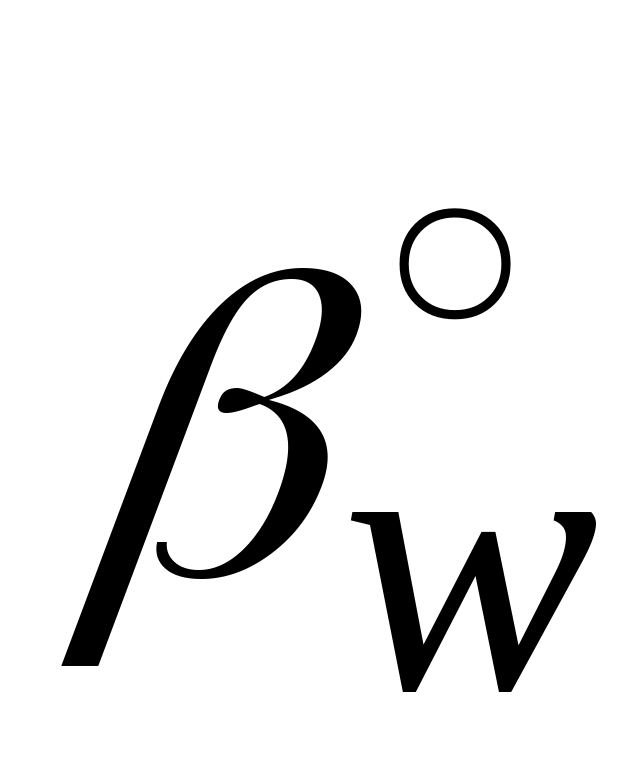 и
и 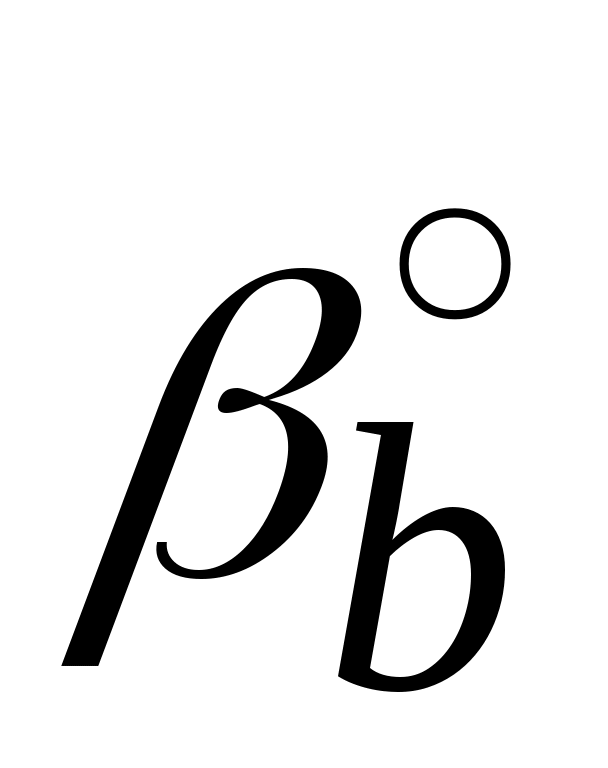 (рис. 82, а). Шаг винтовой линии равен:
(рис. 82, а). Шаг винтовой линии равен:
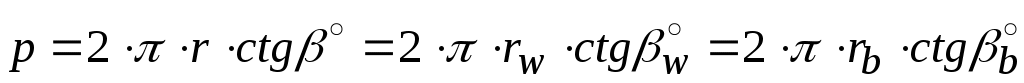 .
.
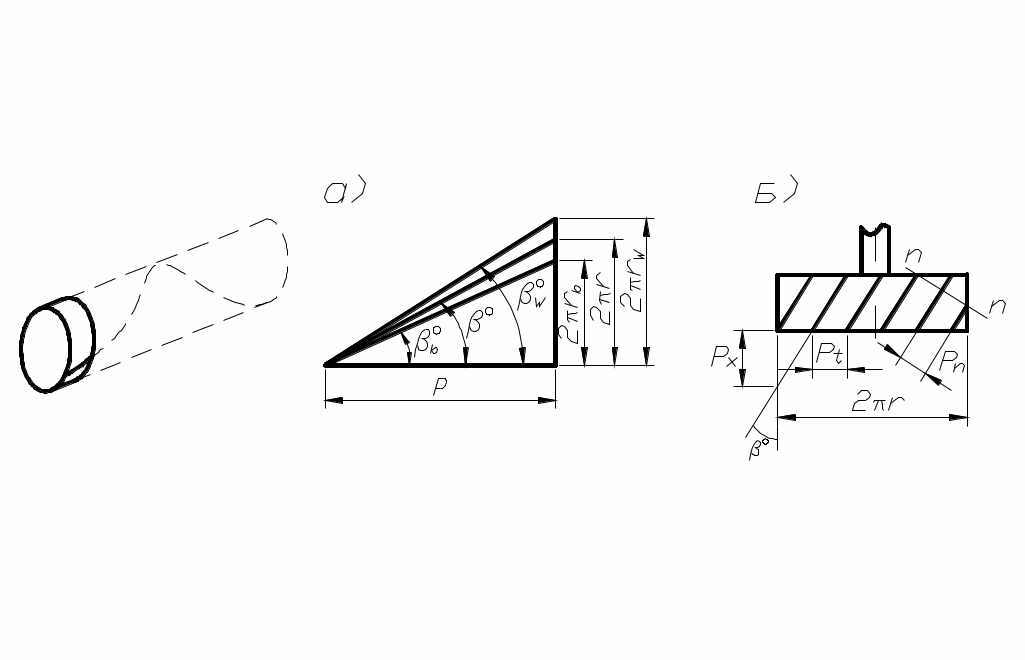
рис. 82
В косозубом колесе различают торцовый mt, нормальный mn и осевой mx модули, причём стандартное значение имеет нормальный модуль mn, соответствующий размерам зуба, замеренным по нормали nn к его оси (рис. 82, б), что объясняется установкой режущего инструмента. Аналогично различают торцовый pt, нормальный pn и осевой px шаг (рис. 82, б), связь между которыми определяется формулами:
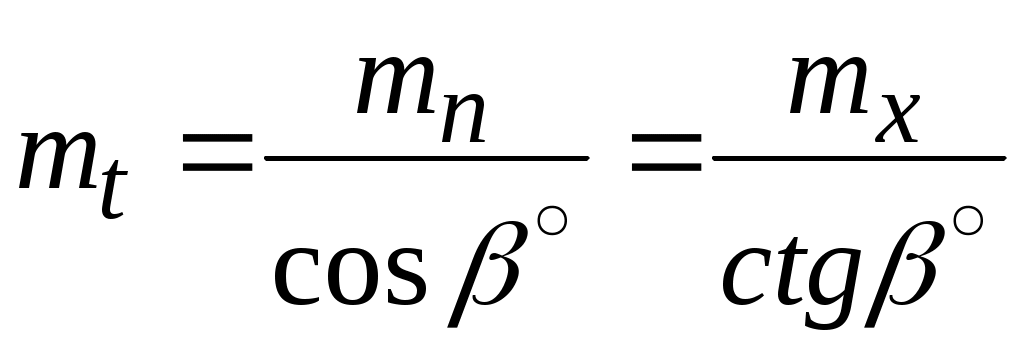 ;
; 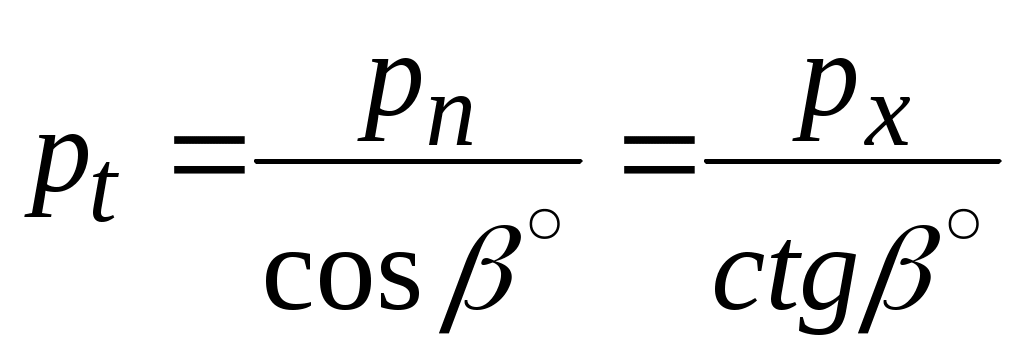 .
.
Большим достоинством зацеплений с косыми зубьями является возможность получения малогабаритных передач. Так, если для прямозубого колеса , то для косозубого
, то для косозубого 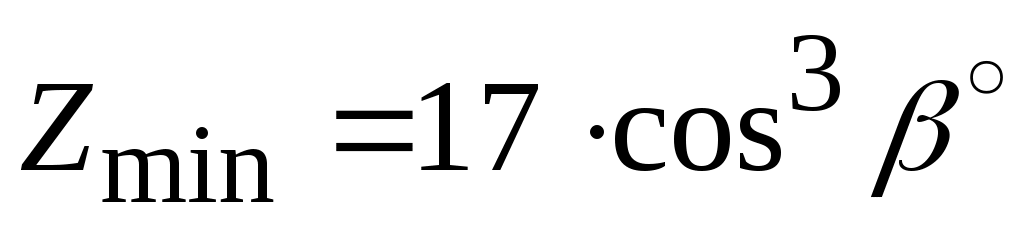 . В экспериментальных конструкциях
. В экспериментальных конструкциях 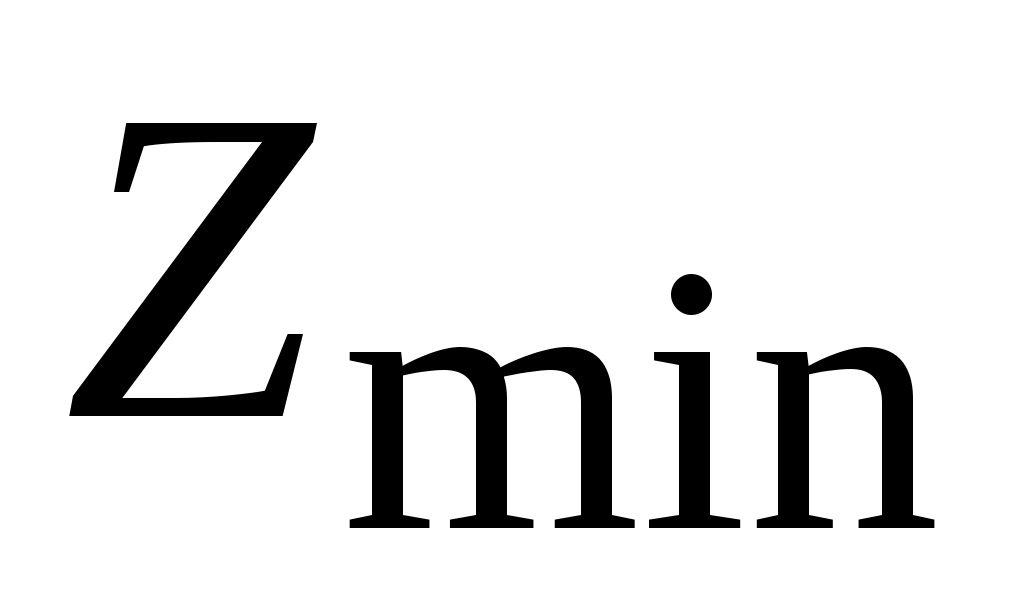
доводят до трёх и менее зубьев. Кроме того, увеличивается коэффициент перекрытия, доходя до 10 и выше, что также повышает нагрузочную способность и позволяет уменьшить габариты передачи. Недостатком является возникновение дополнительных осевых усилий, нагружающих подшипники. Этот недостаток устраняется в шевронных передачах.
8.14. Конические зубчатые передачи
Конические передачи являются передачами с пересекающимися осями вращения звеньев. Применяются, главным образом, передачи с углом между осями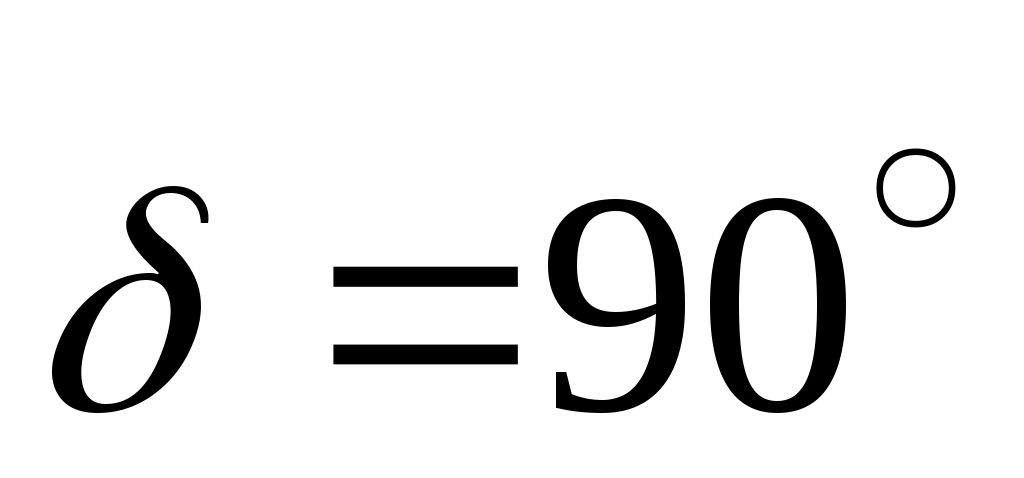 . Основные параметры аналогичны параметрам цилиндрических колёс (рис. 83), причём делительной окружностью стандартного модуля m является внешняя делительная окружность конического колеса диаметром d (рис. 83). Через модуль выражаются все остальные размеры. Для расчёта зубьев на изгиб используется величина среднего модуля, замеренного в середине ширины “в” зубчатого венца. Передаточное отношение равно:
. Основные параметры аналогичны параметрам цилиндрических колёс (рис. 83), причём делительной окружностью стандартного модуля m является внешняя делительная окружность конического колеса диаметром d (рис. 83). Через модуль выражаются все остальные размеры. Для расчёта зубьев на изгиб используется величина среднего модуля, замеренного в середине ширины “в” зубчатого венца. Передаточное отношение равно: 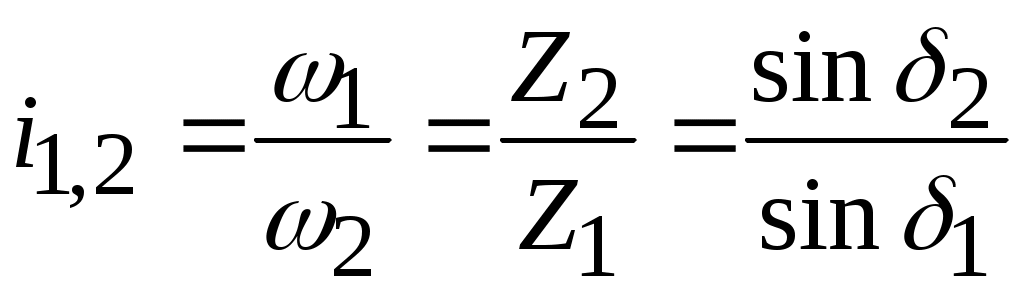 .
.
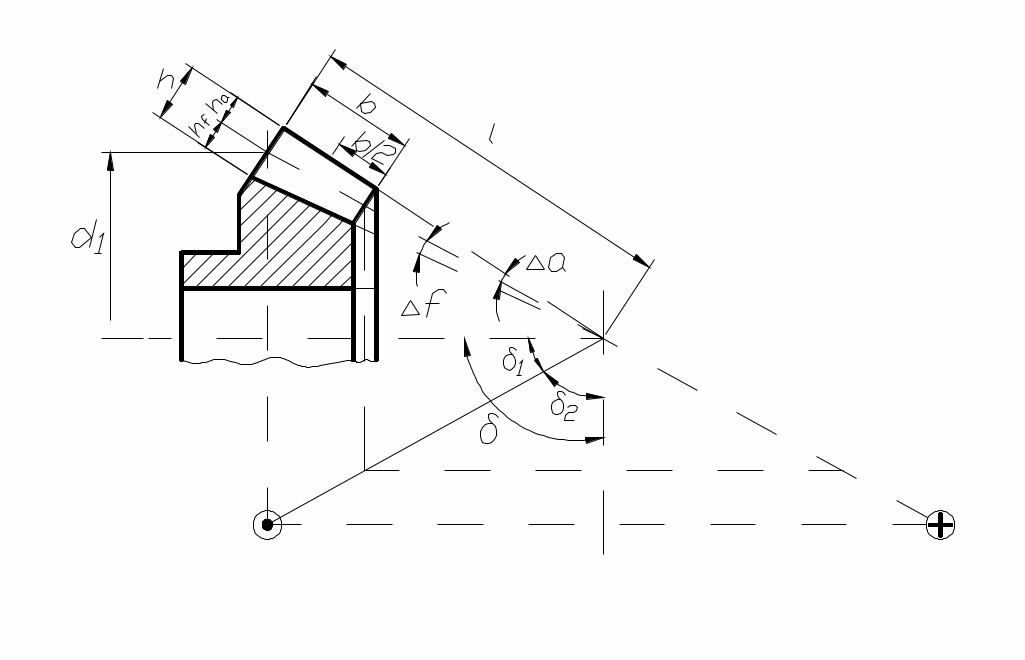
рис. 83
В конических передачах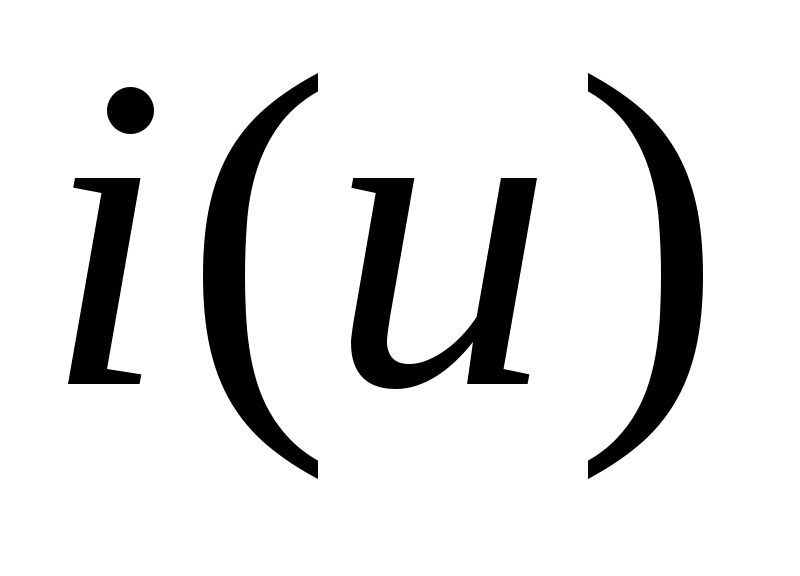 не имеет знака, а для определения направления вращения изображают векторы абсолютных скоростей точек на начальных конусах в виде кружка с точкой (на зрителя) и крестиком (от зрителя), как показано на рис. 83.
не имеет знака, а для определения направления вращения изображают векторы абсолютных скоростей точек на начальных конусах в виде кружка с точкой (на зрителя) и крестиком (от зрителя), как показано на рис. 83.
8.15. Червячные передачи
Червячные передачи являются передачами со скрещивающимися осями. Угол осей обычно равен . Принцип их действия аналогичен передаче винт-гайка.
. Принцип их действия аналогичен передаче винт-гайка.
Червяки подразделяются по числу заходов (винтовых линий) на одно и многозаходные число заходов Z1 совпадает с числом зубьев. Винтовая линия на червяке характеризуется ходом винтовой линии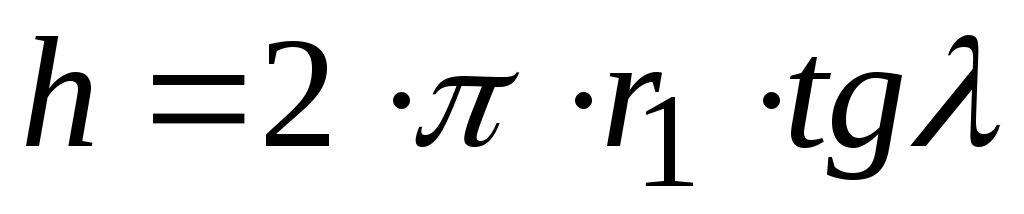 , где r1 – радиус делительной окружности; λ – угол подъёма винтовой линии по делительной окружности (рис. 84, а). Расстояние между двумя соседними витками называется шагом р, причём
, где r1 – радиус делительной окружности; λ – угол подъёма винтовой линии по делительной окружности (рис. 84, а). Расстояние между двумя соседними витками называется шагом р, причём 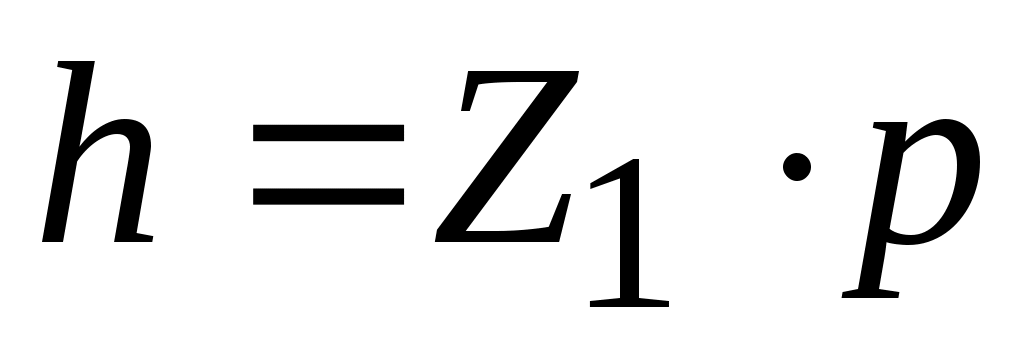 .
.
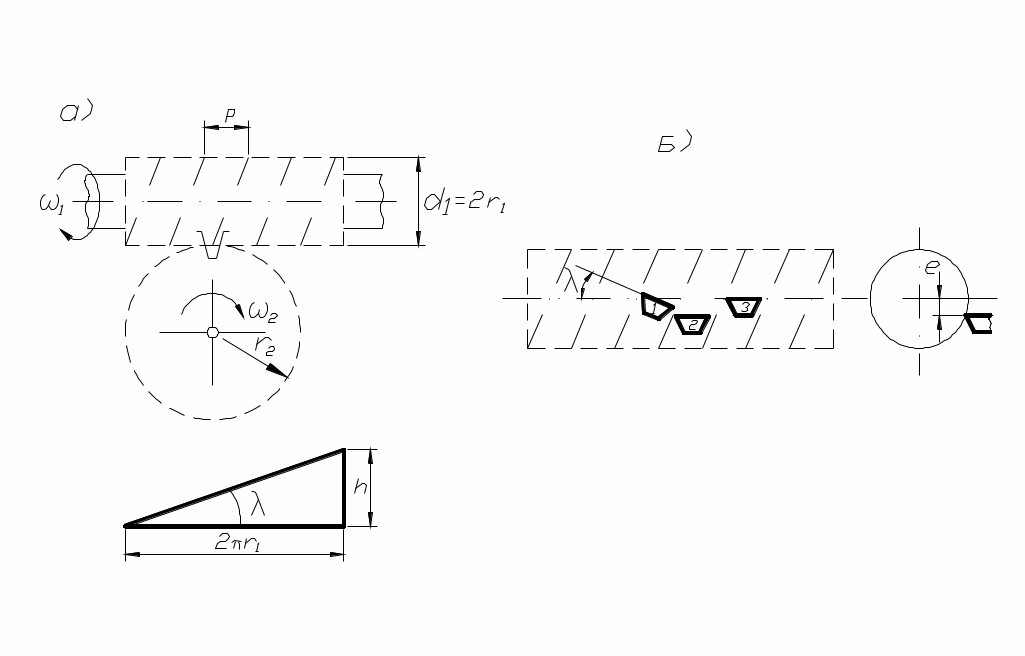
рис. 84
За основной параметр червячного зацепления принимается осевой модуль червяка mS, равный торцевому модулю червячного колеса. Кроме того, стандартным параметром является относительный диаметр червяка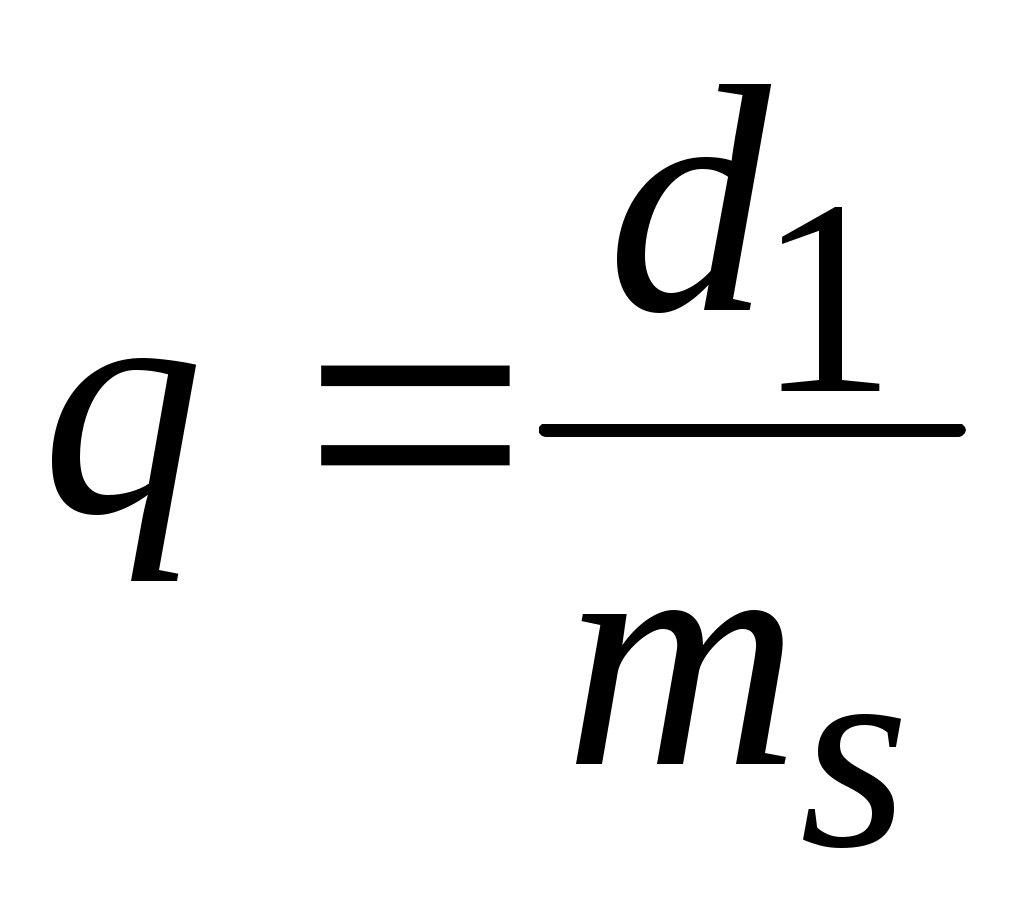 .
.
По форме боковой поверхности резьбы различают конволютный, эвольвентный и архимедов червяки, образуемые при расположении резца трапециевидной формы как указано на рис. 84, б с режущей кромкой под углом λ наклона винтовой линии (1) или при λ=0 и смещении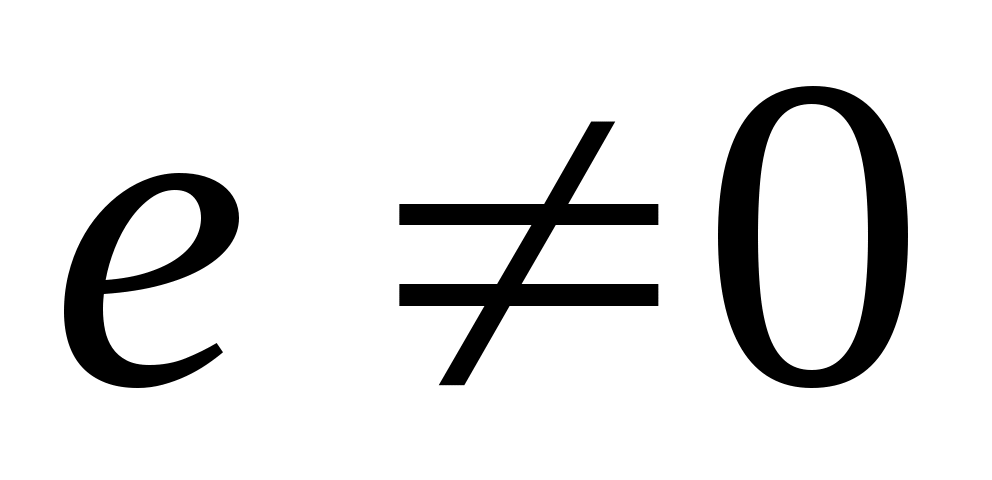 (2), а также при
(2), а также при 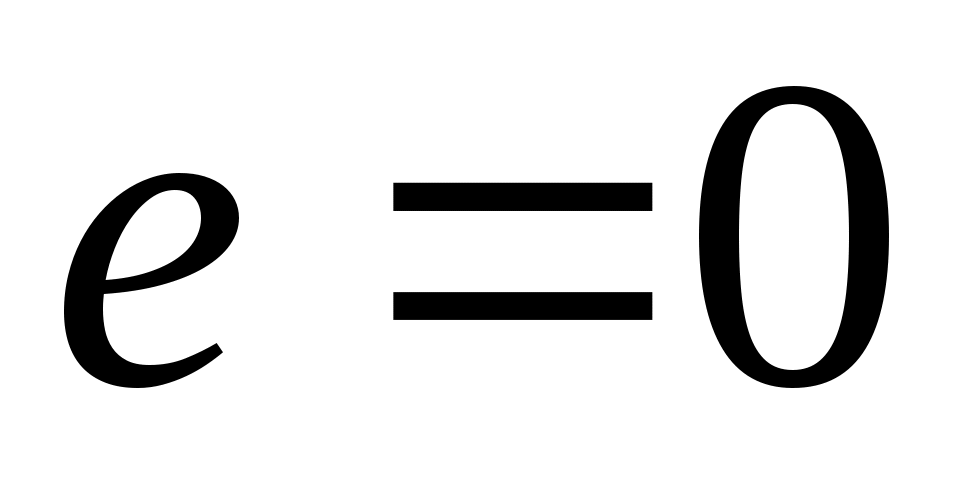 (3). Наименования червяков соответствуют наименованиям кривых, по которым очерчены зубья червяка в сечении, перпендикулярном его оси.
(3). Наименования червяков соответствуют наименованиям кривых, по которым очерчены зубья червяка в сечении, перпендикулярном его оси.
8.16. Кинематический анализ и классификация фрикционных
и зубчатых механизмов
В практике машиностроения чаще возникает необходимость понижения, реже повышения скорости при передаче движения от входного звена к выходному.
Механизмы для передачи вращения, в которых происходит понижение скорости вращения, называются редукторами, а механизмы, повышающие эту скорость, называются мультипликаторами.
По кинематическому признаку различают:
циклические), которые обладают одной степенью свободы (планетарные) или двумя и более (дифференциальные).
Кроме того, различают одно и многоступенчатые механизмы, которые состоят из одной или двух и более пар колёс соединённых последовательно (рис. 85, а), параллельно (рис. 85, б), или смешанно.
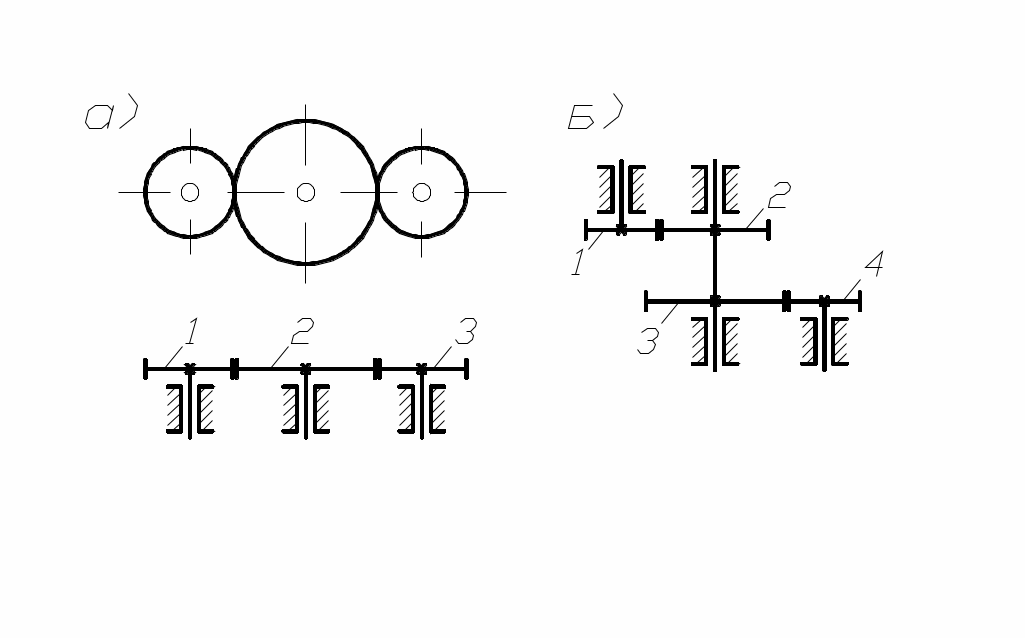
рис. 85
При проектировании механизмов для передачи вращения с заданным значением передаточных отношений и крутящего момента стремятся обеспечить высокий коэффициент полезного действия (кпд), минимальные габариты и вес.
Передаточное отношение одноступенчатого редуктора (при отсутствии скольжения) равно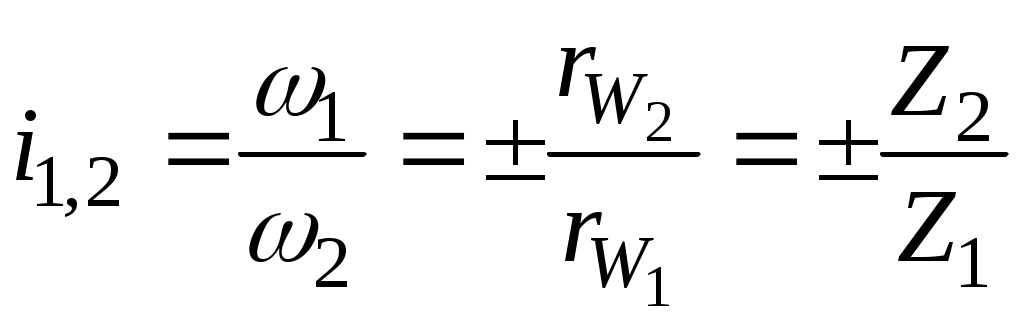
, т.е. отношению радиусов начальных окружностей или отношению чисел зубьев (для зубчатых колёс).
П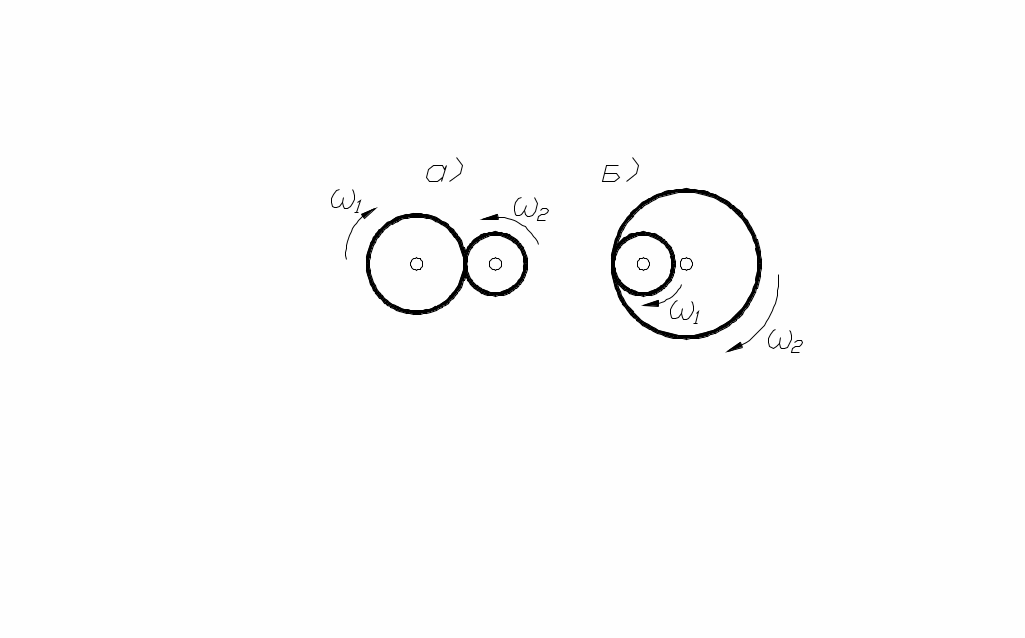 ередаточное отношение берётся со знаком (+), если соприкасающиеся колёса вращаются в одну сторону, и со знаком (-), если – в разные стороны. Обычно знак (+) передаточное отношение имеет при внутреннем касании колёс (рис. 86, б), а знак (-) – при внешнем касании (рис. 86, а). В случае многоступенчатого механизма с па-
ередаточное отношение берётся со знаком (+), если соприкасающиеся колёса вращаются в одну сторону, и со знаком (-), если – в разные стороны. Обычно знак (+) передаточное отношение имеет при внутреннем касании колёс (рис. 86, б), а знак (-) – при внешнем касании (рис. 86, а). В случае многоступенчатого механизма с па-
рис. 86 раллельным соединением колёс (рис. 85, б) получим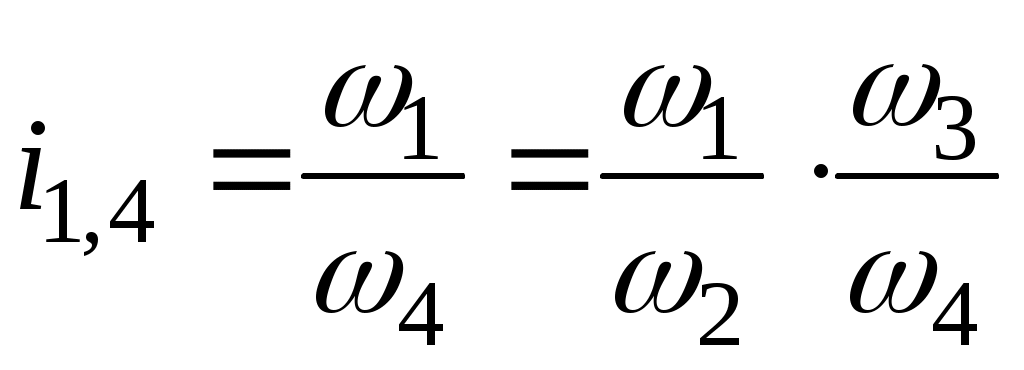 или
или 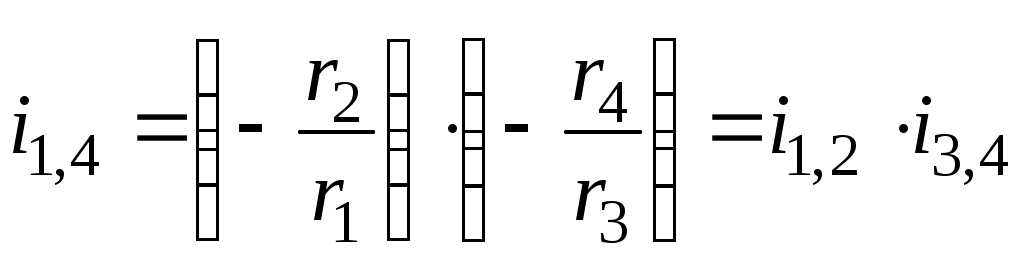 .
.
При последовательном соединении колёс (рис. 85, а)
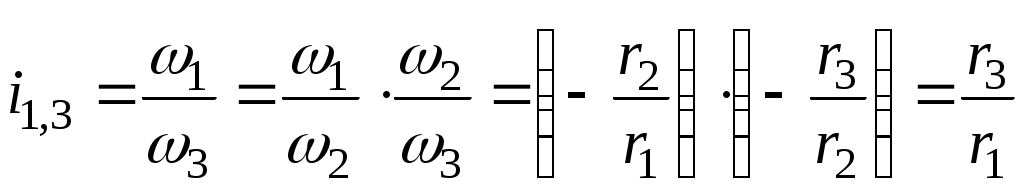 .
.
Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений отдельных ступеней, то есть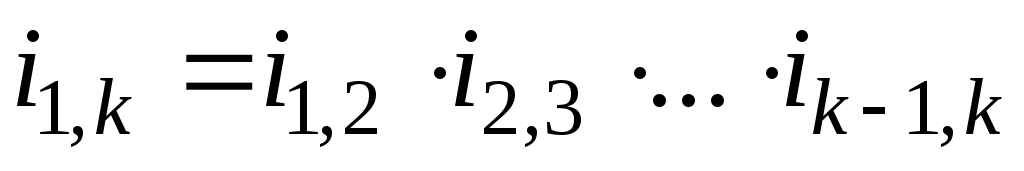 .
.
Причём промежуточные колёса в механизме с последовательным соединением не влияют на величину передаточного отношения, а служат лишь для изменения направления вращения. Эти промежуточные колёса называются паразитными.
Для кинематического анализа механизмов можно использовать графо-численный метод, наглядно иллюстрирующий характер распределения линейных скоростей звеньев механизма. Метод основан на использовании линейной зависимости скорости V от радиуса, т.е.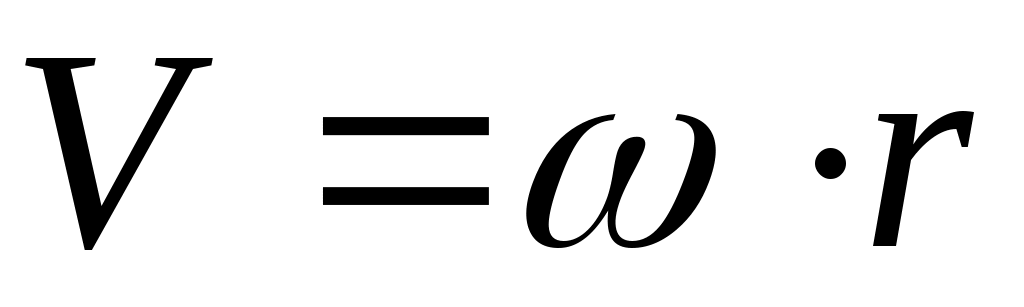 .
.
При построении картины, иллюстрирующей характер распределения линейных скоростей, сначала откладываются в выбранном масштабе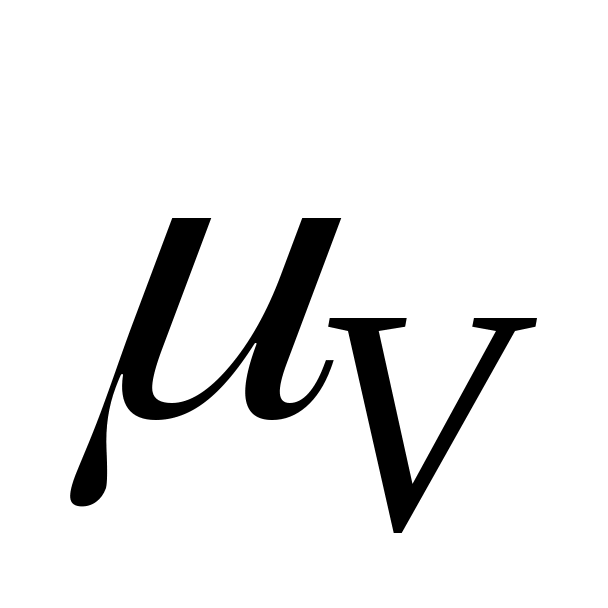 известные вектора линейных скоростей точек, закон движения которых задан (рис. 87).
известные вектора линейных скоростей точек, закон движения которых задан (рис. 87).
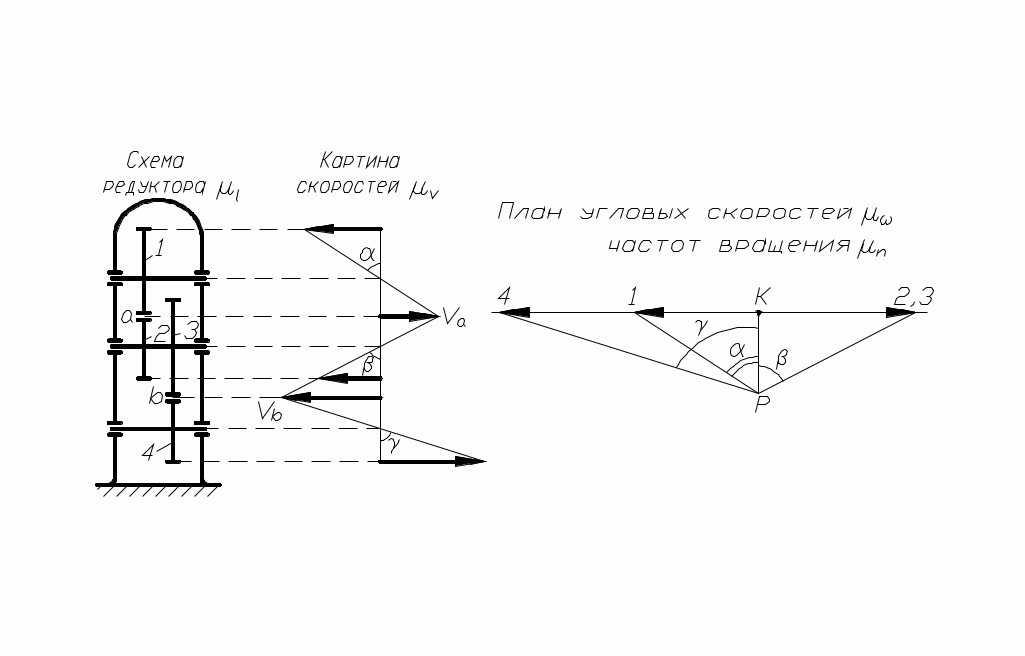
рис. 87
Затем, проводя отрезки через концы векторов известных скоростей, получим общую картину скоростей.
Для определения угловых скоростей (частот вращения) всех звеньев удобно использовать план угловых скоростей (частот вращения), где отрезки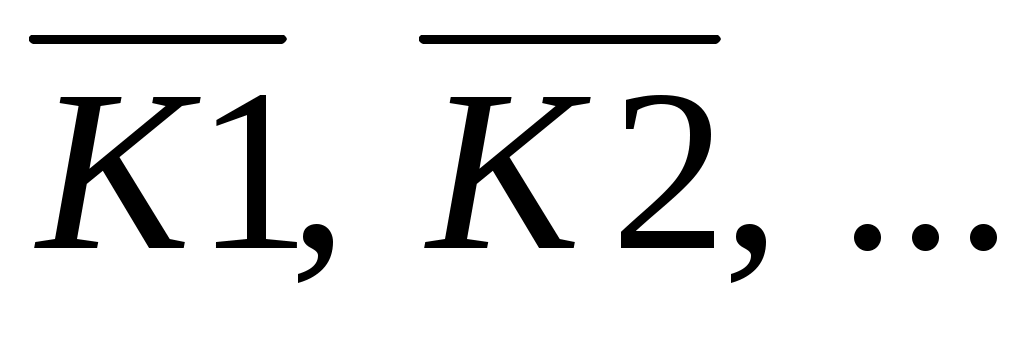
8.12. Выбор расчётных коэффициентов смещения
для передач внешнего зацепления
При назначении коэффициентов смещения χ1 и χ2 для любой передачи должны выполняться три условия:
1) отсутствие подрезания;
2) отсутствие заострения;
3) непрерывность зацепления.
П
 ервое условие выполняется при
ервое условие выполняется при Внутри указанных диапазонов χ назначаются так, чтобы по возможности улучшить качественные показатели передачи (прочность, износостойкость, плавность хода).
Для передачи можно построить область допустимых значений коэффициентов смещения в координатах χ1 и χ2 , которая называется блокирующим контуром. Допустимые значения χ1 и χ2 расположены внутри контура (рис. 81). Для каждой передачи можно построить свой контур. Такие блокирующие контуры для различных передач имеются в справочной литера-
рис. 81 туре.
8.13. Цилиндрические колёса с косыми зубьями и их особенности
Образование косозубого колеса можно представить, если взять цилиндрическое прямозубое колесо и сообщить ему крутильную деформацию. При этом угол скручивания, образованный осью колеса и винтовой линией, является углом наклона винтовой линии βº.
Цилиндрические колёса с косыми зубьями применяются при передаче вращения между параллельными и перекрещивающимися осями. В передаче с параллельными осями углы βº обоих колёс равны по величине и противоположны по направлению при внешнем зацеплении и одинаковы по направлению при внутреннем зацеплении. Угол βº (рис. 82, а) называется углом наклона зубьев по делительному цилиндру радиуса r. С другими соосными цилиндрами, начальным (rw) и основным (rb) винтовая поверхность зуба образует, соответственно, углы

рис. 82
В косозубом колесе различают торцовый mt, нормальный mn и осевой mx модули, причём стандартное значение имеет нормальный модуль mn, соответствующий размерам зуба, замеренным по нормали nn к его оси (рис. 82, б), что объясняется установкой режущего инструмента. Аналогично различают торцовый pt, нормальный pn и осевой px шаг (рис. 82, б), связь между которыми определяется формулами:
Большим достоинством зацеплений с косыми зубьями является возможность получения малогабаритных передач. Так, если для прямозубого колеса
доводят до трёх и менее зубьев. Кроме того, увеличивается коэффициент перекрытия, доходя до 10 и выше, что также повышает нагрузочную способность и позволяет уменьшить габариты передачи. Недостатком является возникновение дополнительных осевых усилий, нагружающих подшипники. Этот недостаток устраняется в шевронных передачах.
8.14. Конические зубчатые передачи
Конические передачи являются передачами с пересекающимися осями вращения звеньев. Применяются, главным образом, передачи с углом между осями

рис. 83
В конических передачах
8.15. Червячные передачи
Червячные передачи являются передачами со скрещивающимися осями. Угол осей обычно равен
Червяки подразделяются по числу заходов (винтовых линий) на одно и многозаходные число заходов Z1 совпадает с числом зубьев. Винтовая линия на червяке характеризуется ходом винтовой линии

рис. 84
За основной параметр червячного зацепления принимается осевой модуль червяка mS, равный торцевому модулю червячного колеса. Кроме того, стандартным параметром является относительный диаметр червяка
По форме боковой поверхности резьбы различают конволютный, эвольвентный и архимедов червяки, образуемые при расположении резца трапециевидной формы как указано на рис. 84, б с режущей кромкой под углом λ наклона винтовой линии (1) или при λ=0 и смещении
8.16. Кинематический анализ и классификация фрикционных
и зубчатых механизмов
В практике машиностроения чаще возникает необходимость понижения, реже повышения скорости при передаче движения от входного звена к выходному.
Механизмы для передачи вращения, в которых происходит понижение скорости вращения, называются редукторами, а механизмы, повышающие эту скорость, называются мультипликаторами.
По кинематическому признаку различают:
-
механизмы с неподвижными геометрическими осями всех колёс (рядовые); -
механизмы с подвижными геометрическими осями некоторых колёс (эпи-
циклические), которые обладают одной степенью свободы (планетарные) или двумя и более (дифференциальные).
Кроме того, различают одно и многоступенчатые механизмы, которые состоят из одной или двух и более пар колёс соединённых последовательно (рис. 85, а), параллельно (рис. 85, б), или смешанно.
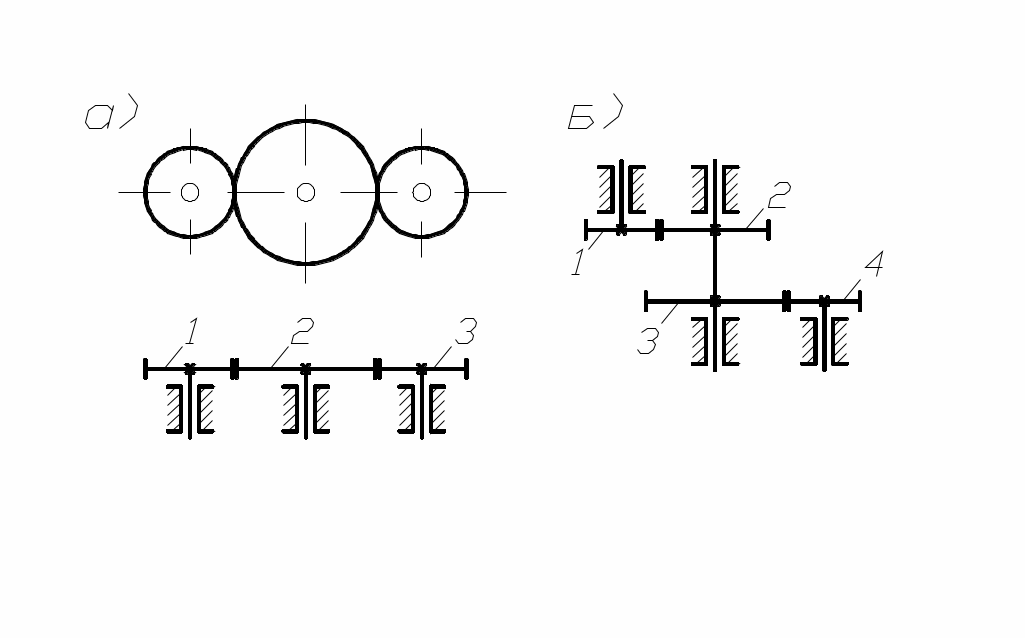
рис. 85
При проектировании механизмов для передачи вращения с заданным значением передаточных отношений и крутящего момента стремятся обеспечить высокий коэффициент полезного действия (кпд), минимальные габариты и вес.
Передаточное отношение одноступенчатого редуктора (при отсутствии скольжения) равно
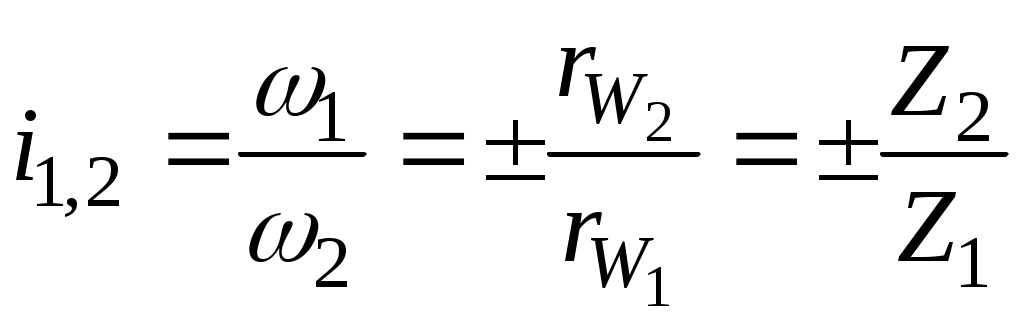
, т.е. отношению радиусов начальных окружностей или отношению чисел зубьев (для зубчатых колёс).
П
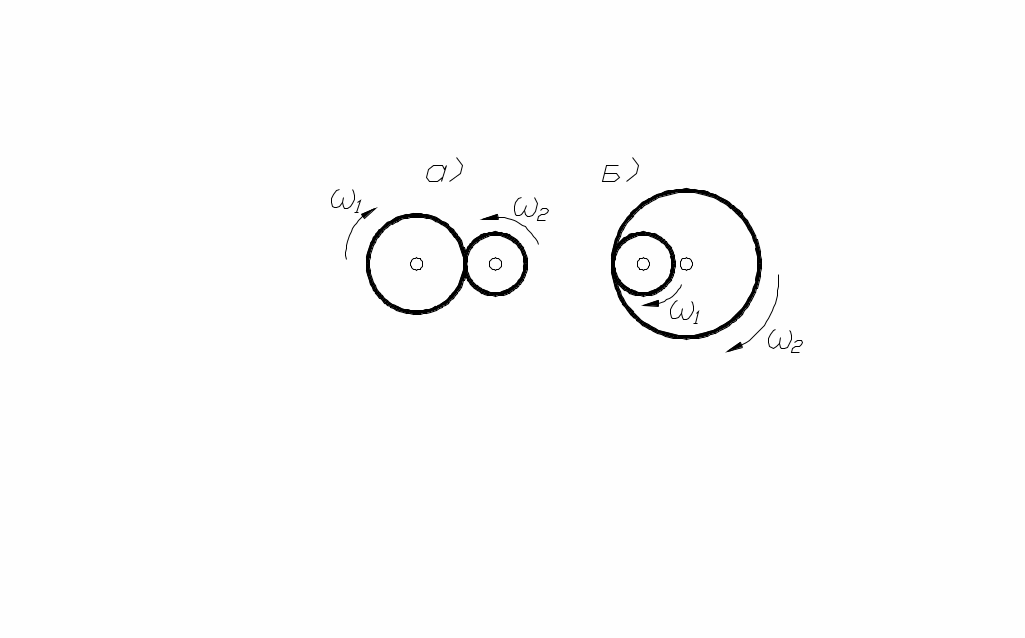 ередаточное отношение берётся со знаком (+), если соприкасающиеся колёса вращаются в одну сторону, и со знаком (-), если – в разные стороны. Обычно знак (+) передаточное отношение имеет при внутреннем касании колёс (рис. 86, б), а знак (-) – при внешнем касании (рис. 86, а). В случае многоступенчатого механизма с па-
ередаточное отношение берётся со знаком (+), если соприкасающиеся колёса вращаются в одну сторону, и со знаком (-), если – в разные стороны. Обычно знак (+) передаточное отношение имеет при внутреннем касании колёс (рис. 86, б), а знак (-) – при внешнем касании (рис. 86, а). В случае многоступенчатого механизма с па- рис. 86 раллельным соединением колёс (рис. 85, б) получим
При последовательном соединении колёс (рис. 85, а)
Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений отдельных ступеней, то есть
Причём промежуточные колёса в механизме с последовательным соединением не влияют на величину передаточного отношения, а служат лишь для изменения направления вращения. Эти промежуточные колёса называются паразитными.
Для кинематического анализа механизмов можно использовать графо-численный метод, наглядно иллюстрирующий характер распределения линейных скоростей звеньев механизма. Метод основан на использовании линейной зависимости скорости V от радиуса, т.е.
При построении картины, иллюстрирующей характер распределения линейных скоростей, сначала откладываются в выбранном масштабе

рис. 87
Затем, проводя отрезки через концы векторов известных скоростей, получим общую картину скоростей.
Для определения угловых скоростей (частот вращения) всех звеньев удобно использовать план угловых скоростей (частот вращения), где отрезки