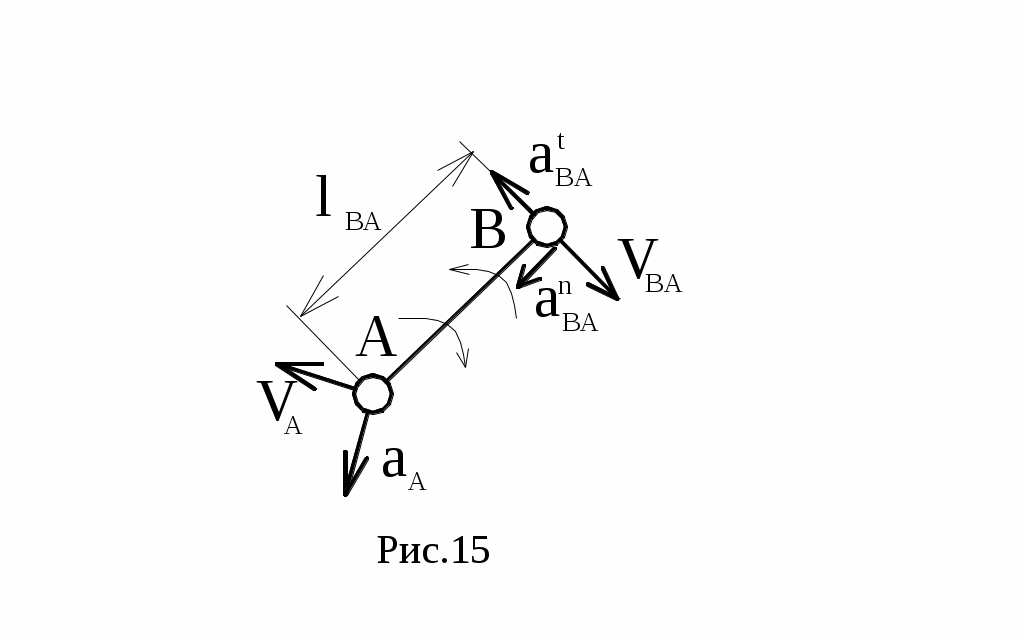а) звено совершает плоскопараллельное движение, состоящее из переносного, т.е. поступательного со скоростью полюса и относительного вращательного вокруг полюса (рис.15).

Принимая за полюс т. A, получим:

V_B=V_A+V_BA; где V_BA=·l_AB;

a_B=a_A+a_BA; где a_BA=aⁿ_BA+a^t_BA при

aⁿ_BA=²·l_AB; a^t_BA=·l_AB.

Здесь V, a, ,  - линейные скорости и ускорения соответствующих характерных точек, а также угловые скорость и уско-

рение звена (индексы соответствуют ха-

рактеру ускорений и обозначениям точек).

б 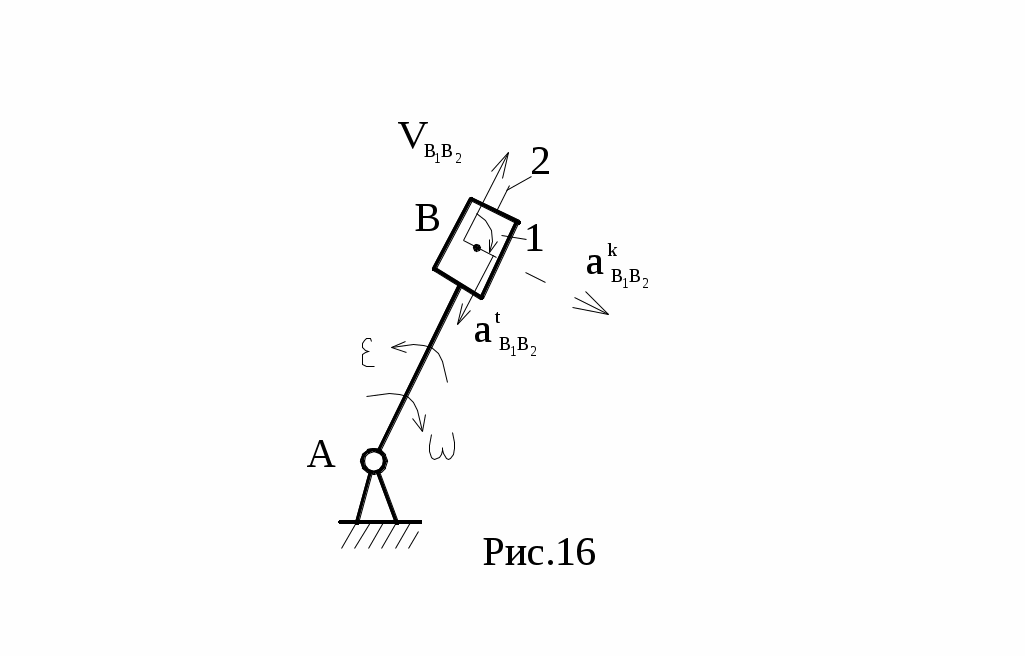) звено совершает сложное движение, состоящее из переносного вращательного и относительного поступательного, например, звено 1 (рис.16).

Пусть B₁ и B₂ – точки, принадлежащие звеньям 1 и 2. Тогда:

V_B1=V_B2+V_B1B2, где V_B2=·l_AB.

a_B1=a_B2+a^t_B1B2+a^k_B1B2, где ускорение Кориолиса

a^k_B1B2=2V_B1B2· и совпадает с направлением вектора V_B1B2, повернутого на 90^○ в сторону переносного вращения.

Решение векторных уравнений осуществляется графически путем построения так называемых планов скоростей и ускорений, на которых абсолютные скорости и ускорения откладываются от одной точки, называемой полюсом, в определенном масштабе.

---

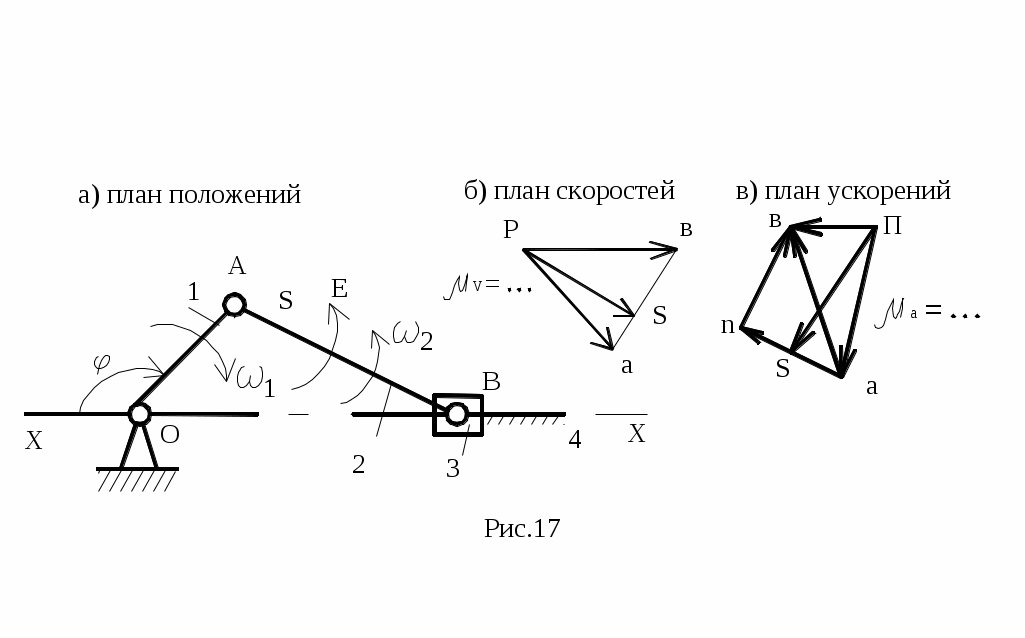
Пример расчета кривошипно-ползунного механизма рассмотрен на рис.17, где план положений (рис.17, а), план скоростей и ускорений (рис.17, б, в).

Векторные уравнения для скоростей записываются в виде:

V_B=V_A+V_BA; V_B=V_Bx+V_BBx;

где V_A=₁·l_OA; V_Bx=0; V_BA_|_AB; V_BBx||x-x,

т.е. в выбранном масштабе μ_V: pb||x-x; ab_|_AB

V_BA= μ_V·ab; V_B= μ_V·pb и ₂= V_BA/ l_AB.




Векторные уравнения для ускорений при ₁=const записываются в виде:

a _B=a_A+a_BA; a_B=a_Bx+a^k_BBx+a^t_BBx; где a_A=aⁿ_A=₁²·l_OA; a_BA=aⁿ_BA+a^t_BA;

здесь aⁿ_BA=₂²·l_AB; a^t_BA=ε₂·l_AB; a_Bx=0; a^k_BBx=0; a^t_BBx||x-x.

Все ускорения представлены на рис.17 в выбранном масштабе μ_a в виде соответствующих отрезков, например, a_B=μ_a·πb и т.д.


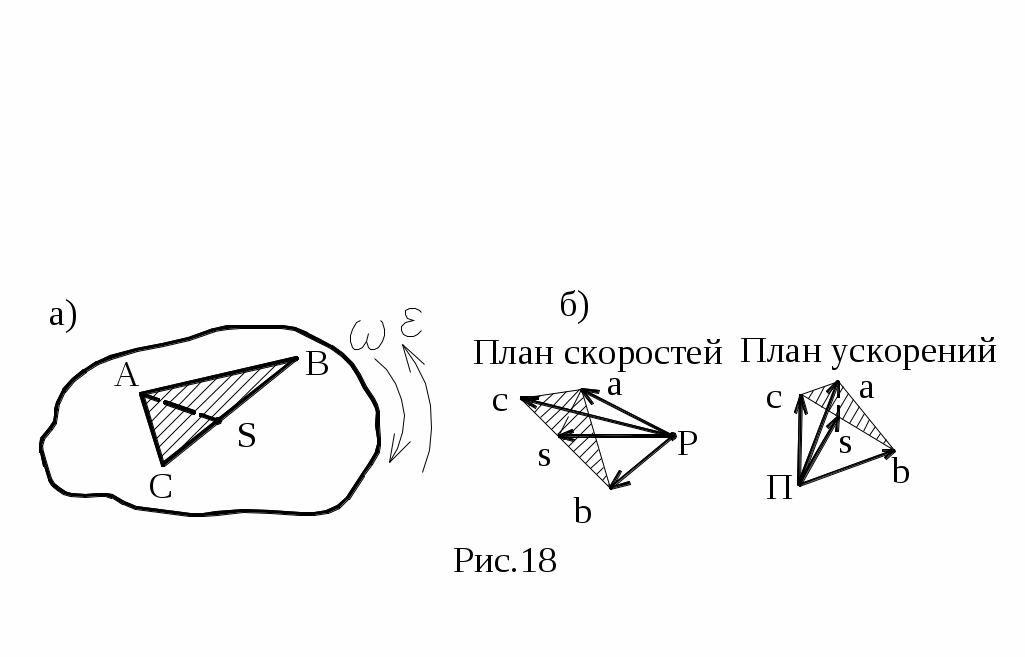
При определении скоростей и ускорений промежуточных точек звеньев, например т. S, можно использовать так называемую теорему подобия, согласно которой точки на плане положений звеньев и соответственные точки на планах скоростей и ускорений образуют подобные фигуры или пропорциональные отрезки. Рассмотрим доказательство данной теоремы. На рис.18 показано звено ABC и планы скоростей и ускорений для точек этого звена:

---

отрезок ca на плане скоростей соответствует V_CA_|_CA;

отрезок ab на плане скоростей соответствует V_AB_|_AB;

отрезок bc на плане скоростей соответствует V_BC_|_BC;

т.е. треугольник abc подобен треугольнику ABC.

Ускорения относительного (вращательного) движения равны:

; ; ,

т.е. a_CA/ l_CA =a_AB/ l_AB =a_BC/ l_BC или ca/CA=ab/AB=bc/BC,

Следовательно, треугольник abc подобен треугольнику ABC. Аналогичным является построение фигур для любой промежуточной точки, например т. S (рис.18, а, б).
4.3. Исследование рычажных механизмов методом

кинематических диаграмм
Кинематической диаграммой называется графическая зависимость какого-либо параметра движения звена от времени или от перемещения входного звена, представленные в определенной системе координат.

Если известна одна кинематическая диаграмма, то можно получить остальные зависимости путем графического дифференцирования или интегрирования.

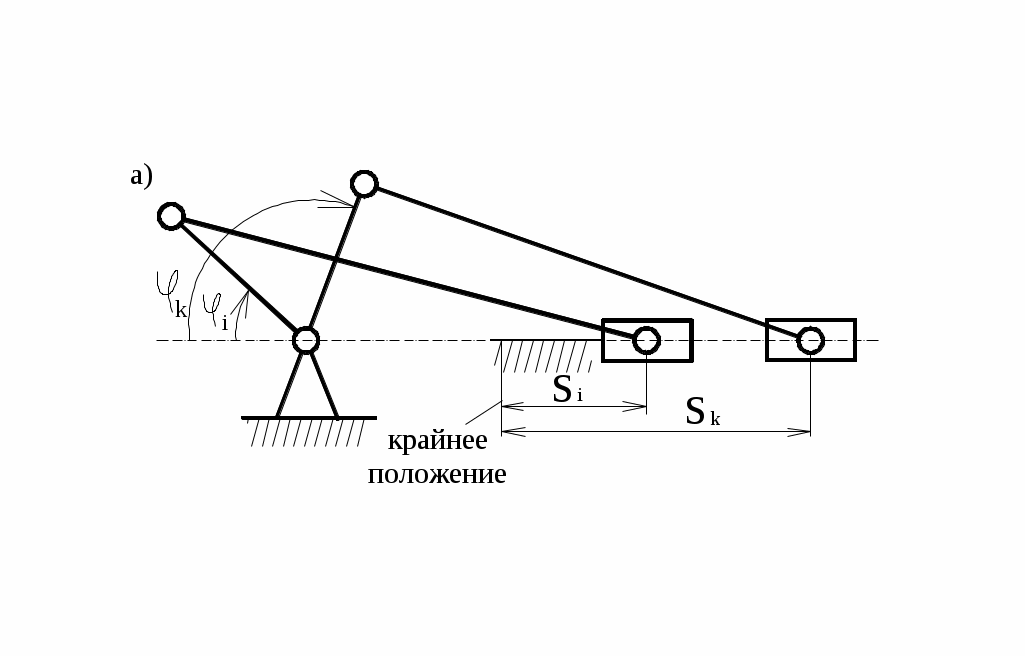
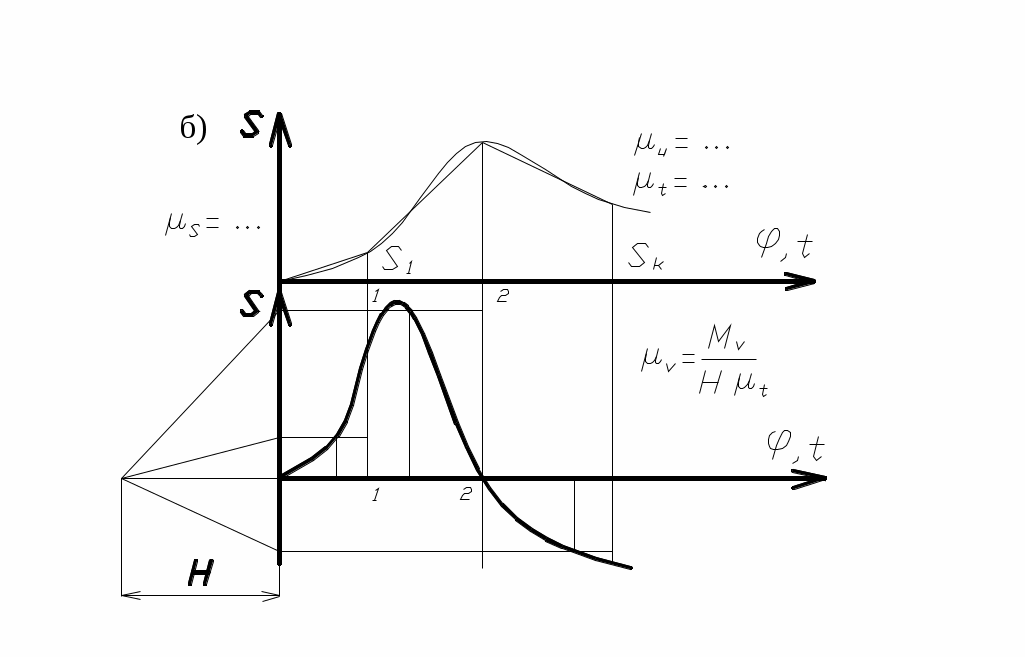На рис.19, а, б показана последовательность построе­ния кинематической диа­граммы перемещения ползуна кривошипно-ползунного меха­низма S(φ) и S(t), а также эле­менты графического дифферен­цирования с получе­нием диаграммы скоростей V(t) методом хорд.

Если диаграмма V(t) пер­вична, то процесс, обратный интегрированию, обеспечит получение диаграммы S(t) и называется графическим интег-рированием.

Следует отметить, что графические методы часто приводят к искажениям резуль-

Рис. 19 татов из-за неточности графических построений, поэтому необходимо контролировать расположение характерных точек, соответствующих экстремумам на диаграммах.
4.4. Кинематическое исследование рычажных механизмов

аналитическим методом
Аналитические методы исследования позволяют проводить анализ с заданной степенью точности. Кроме того, создание математических моделей механизмов позволяет решать задачи их оптимального синтеза при использовании ЭВМ.

---

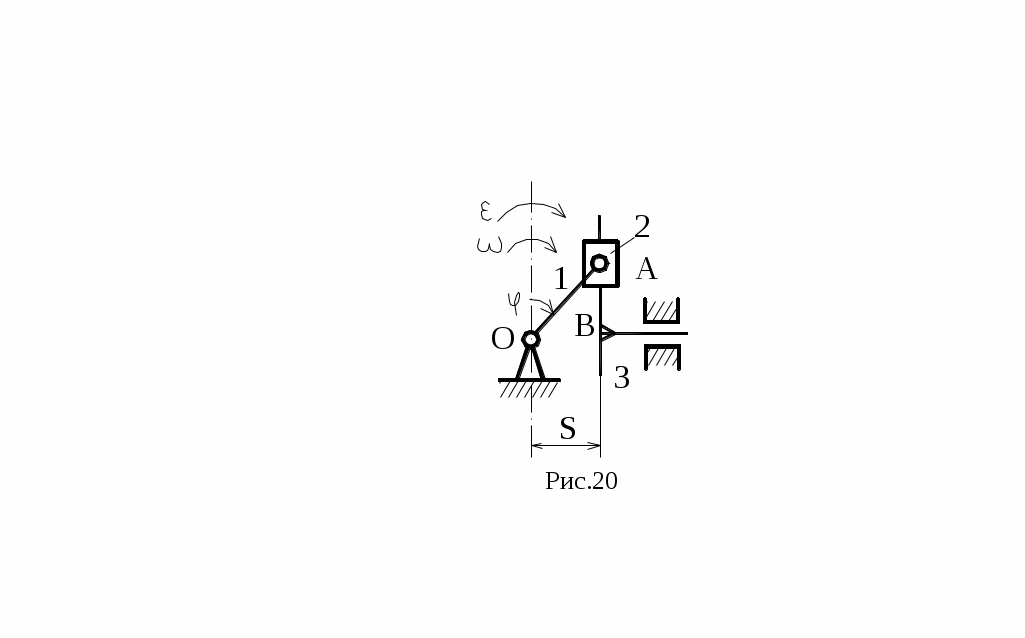Рассмотрим пример кинематического исследования синусного механизма (механизм двойного ползуна), где кривошип 1 вращается с угловой скоростью ω и угловым ускорением ε (рис.20).

Тогда скорость и ускорение точки А равны:

V_A=l_OA·ω; .

Все точки звена 1 и 2 описывают окружности, а точки звена 3 движутся поступательно, имея перемещения, скорости и ускорения равные:

S_B=l_OA·sinφ=l_OA·sinωt; V_B=dS_B/dt=dS_B·dφ/dφ·dt=l_OA·ω·cosφ;

a_B=d²S_B/dt=l_OA·(ε·cosφ-ω²·sinφ)

при ε=0 a_B=-l_OA·ω²·sinφ.

При исследовании многих механизмов получаются достаточно громоздкие формулы, что не является препятствием при использовании ЭВМ.

При исследовании пространственных механизмов используются элементы векторной алгебры и векторного анализа. Положения, скорости и ускорения точек механизма выражаются в векторной форме, при необходимости вычисляются проекции на оси и плоскости. Примеры таких исследований изложены в учебной литературе.
5. Динамический анализ рычажных механизмов
5.1. Классификация действующих сил
Среди сил, действующих на механизм, различают:

а) движущие силы F_д или моменты M_д, ускоряющие движение входных (начальных) звеньев и совершающие положительную работу. Например: силы давления газа на поршень в двигателе внутреннего сгорания, силы веса при опускании груза и т.д.

б) силы сопротивления F_c или моменты М_с, замедляющие движение входных звеньев и совершающие отрицательную работу. Они могут быть силами полезного сопротивления, дающими производственный эффект, и силами вредного сопротивления не дающими такого эффекта. К первому типу относятся например, силы тяжести при подъеме груза, а ко второму типу – силы трения.

в) силы реакции в кинематических парах F_ij, возникающие в опорах звеньев и являющиеся внутренними силами для механизма в целом и внешними для каждого отдельного звена.

г) силы инерции F_и или моменты сил инерции M_и возникают при переменном движении звеньев механизма и могут быть как движущими, так и силами сопротивления (в зависимости от их направления относительно направления движения звеньев). Фактически эти силы действуют на тело, вызывающее ускорение другого тела. Однако, условное приложения сил инерции к ускоряемому телу позволяет рассматривать его в равновесии. Этот принцип – принцип Даламбера позволяет задачу динамики свести к статическому расчету.

---

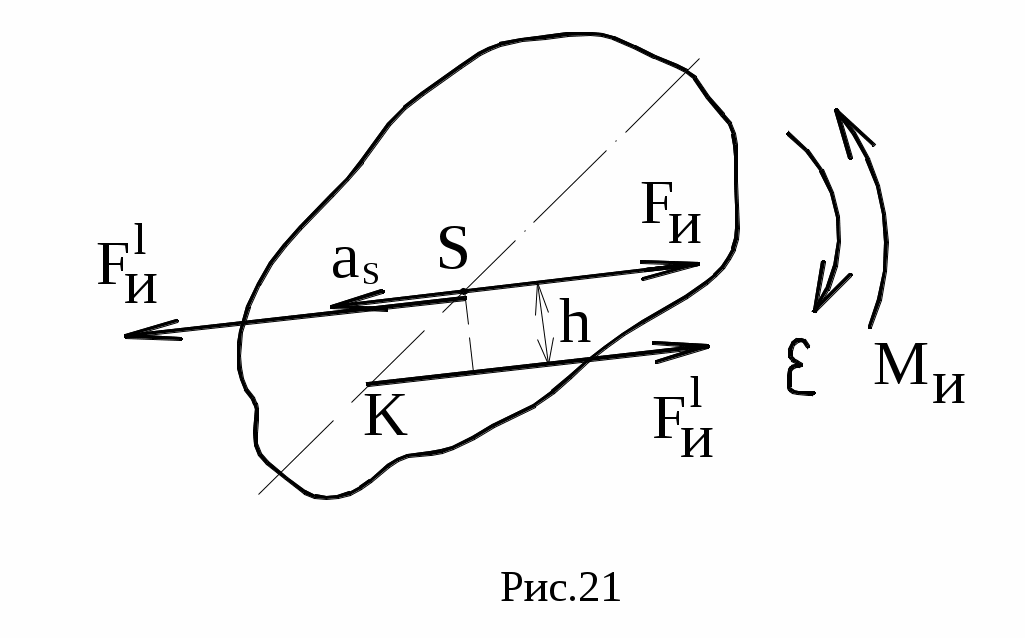Силы инерции относятся к категории распределенных или так называемых массовых сил, которые как и другие аналогичные силы могут быть приведены к главному вектору и главному моменту (рис.21).

F_и =-ma_s; M_и=-J_S·ε; где m и J_S – масса и момент инерции звена относительно оси, про-ходящей через центр масс;

a_S – ускорение центра масс;

ε – угловое ускорение звена.

Знаки (-) показывают, что направления F_и и М_и противоположны соответствующим ускорениям.

Сила F_и и момент М_и, могут быть заменены одной силой F_и^/=F_и, линия действия которой проходит через так называемый центр качаний (точка К на рис.21) на оси звена и отстоит от линии действия F_и на расстоянии h=М_и/F_и при замене М_и парой сил F_и^/.
5.2. Приведение сил и масс в механизме
Для исследования закона движения механизма его удобно заменить одним условным звеном – звеном приведения, имеющим закон движения аналогичного звена реального механизма.

Все внешние силы, действующие на звенья при этом заменяются одной приведенной силой F_∑^пр или моментом М_∑^пр , мощности Р_∑^пр которых равны мощностям Р_i заменяемых сил F_i и моментов сил M_i, т.е.

Р_∑^пр=∑Р_i, где Р_i=F_i·V_i·cos(F_iV_i) или Р_i=М_i·ω_i;

Р_∑^пр=F_∑^пр·V·cos(F_∑^прV) или Р_∑^пр=М_∑^пр·ω.

Здесь V_i и V – скорости точек приложения соответствующих сил; ω_i и ω – угловые скорости i-го звена и звена приведения.

Суммарную приведенную силу или момент удобно записывать в виде составляющих, например: М_∑^пр=∑М_Fi^пр+∑М_Мi^пр, где каждая составляющая определяется из соответствующего равенства мощностей:

М_Fi^пр=F_i·V_i/ω·cos(F_iV_i) - для силы F_i;

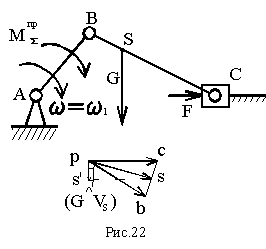
М_Мi^пр=М_i·ω_i/ω - для момента М_i;

Пример кривошипно-ползунного механизма (рис.22): М_∑^пр=М_F^пр+M_G^пр,

где М_F^пр=F·V_C/ω₁=F·l_AB·рс/pb;

---

Смотрите также файлы

• Новостная справка за прошедшую неделю о событиях на Донбассе.docx

• Цель занятия закрепление знаний о нормативноправовых основах взаимодействии воспитателя с сотрудниками детского сада, формирование умения применять полученные знания на практике Задание 1.docx

• Guardians of Cloudia.docx

• "политика".docx

• Вавававававававакваапмвпвапвававававававававававаавваваававвааылзщвчсвва.docx