Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 145
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
MGпр=G·VS/ω1·cos(G^VS)=G·lAB·ps/pb.
Здесь pb, pc, ps|=ps·cos(G^VS) – вектора, взятые с плана скоростей (рис.22).
Как видно из формул, величина Fпр (Мпр) зависит лишь от соотношения скоростей, а не от их абсолютной величины, что позволяет для приведения сил использовать планы скоростей без учета их масштабов. Каждое i-ое звено механизма обладает массой mi и моментом инерции Ji относительно оси, проходящей через центр масс звена, при этом кинетическая энергия i-го звена плоского механизма равна:
Ti=(mi·Vi2/2)+Ji·ωi2/2.
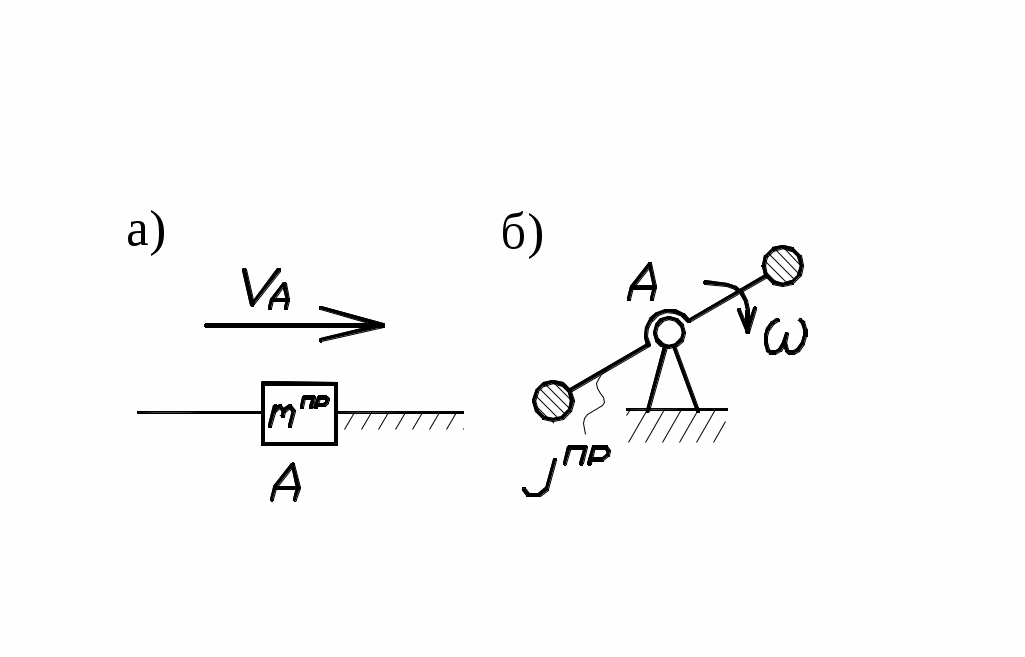 Массы и моменты инерции всех звеньев механизма можно условно заменить некоторой массой mпр, сосредоточенной в произвольно выбранной точке А звена приведения (рис.23, а) или некоторым моментом инерции Jпр, приписанным звену
Массы и моменты инерции всех звеньев механизма можно условно заменить некоторой массой mпр, сосредоточенной в произвольно выбранной точке А звена приведения (рис.23, а) или некоторым моментом инерции Jпр, приписанным звену
Рис. 23 приведения (рис.23, б).
Замена должна производится из условия равенства кинетических энергий:
Тпр=Тмех=∑Тi,
где Тпр=mпр·VA2/2 или Тпр=Jпр·ω2/2,
т.е. mпр=∑[mi·(Vi/VA)2+Ji·(ωi/VA)2] – при поступательном движении звена приведения.
Jпр=∑[ mi·(Vi/ω)2+Ji·(ωi/ω)2] – при вращательном движении звена приведения.
mпр и Jпр являются функциями положения звена приведения, т.е. их величина может меняться при изменении положения звена в процессе его движения.
5.3. Уравнение движения машины
Работу машины можно разбить на 3 периода:
Аналитическая зависимость между действующими на звенья силами и кинематическими параметрами движения называется уравнением движения. Это уравнение в общем случае имеет вид ∆Т=Ад-Ас, где ∆Т=Т-Т0 – изменение кинетической энергии за рассматриваемый промежуток времени (Т и Т0 – величина кинетической энергии в конце и начале промежутка);
Ад-Ас – суммарная работа действующих сил за рассматриваемый промежуток (Ад, Ас – работа движущих сил и сил сопротивления).
В период пуска Ад-Ас=∆Т>0, т.е. происходит ускорение движения звеньев, являющегося неустановившемся.
В период установившегося движения Ад-Ас=∆Т=0, т.е. скорости звеньев в конечный и начальный моменты цикла равны и вся работа движущихся сил расходуется на преодоление сопротивлений.
В период остановки Ад-Ас=∆Т<0, движение продолжается некоторое время за счет накопленной кинетической энергии, поглощаемой за счет сопротивления движению.
Уравнение движения может быть выражено в интегральной и дифференциальной форме, а для упрощения его решения исследование машины заменяют исследованием звена приведения, в котором изменение кинетической энергии равно: ∆Tпр =Адпр-Аспр, где суммарная работа действующих на звено приведения сил может быть выражена:
а) в интегральной форме:
Адпр-Аспр=∫F∑прds или Адпр-Аспр=∫M∑прdφ;
б) в дифференциальной форме:
dTпр=M∑прdφ или M∑пр=dTпр/dφ;
т.е. при dTпр=1/2·Jпр·ω2 получим:
M∑пр=(dJпр/dφ)·(ω2/2)+Jпр·ω·(dω/dφ)·(dt/dt)=(dJпр/dφ)·(ω2/2)+ε·Jпр.
Таким образом, уравнение движения машины приводится к тому или иному конкретному виду и решается графическим и графоаналитическим методами, а учитываемые силы и моменты сил, а также приведенные массы и моменты инерции могут быть как постоянными так и переменными величинами, зависящими от того или иного фактора.
5.4. Понятие об уравновешивающей силе.
Теорема Жуковского о жестком рычаге
Одним из способов определения приведенной силы Fпр является способ, предложенный проф. Н.Е. Жуковским. Уравнение, из которого может быть найдена Fпр, основано на равенстве мощностей: F∑пр·VA·cos(F∑пр VA)=∑Fi·Vi·cos(Fi Vi).
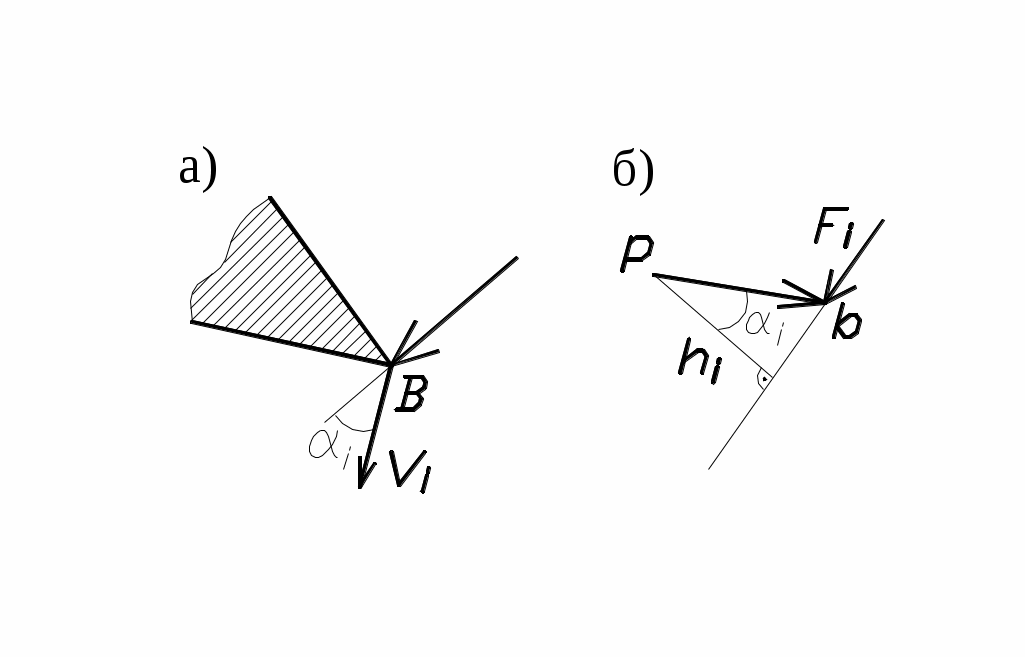 Рассмотрим какое-либо звено механизма, в т. В которого приложена сила Fi под углом αi к вектору скорости Vi этой точки (рис.25, а).
Рассмотрим какое-либо звено механизма, в т. В которого приложена сила Fi под углом αi к вектору скорости Vi этой точки (рис.25, а).
Мощность силы Fi равна:
Pi=Fi·Vi·cosαi.
Если вектор скорости т. В (план скоростей) повернуть на
Рис. 25 90˚ и силу Fi приложить к концу вектора (в т. «b»), сохранив ее направление, то момент этой силы относительно полюса «p» будет равен (рис.25, б): Mi=Fi·hi=Fi·Vi·cosαi=Pi,
т.е. равен мощности силы Fi. Таким образом, Fi можно найти, повернув на 90˚ план скоростей и приложив к нему все внешние силы, включая силы инерции, в соответствующих точках и сохраняя их направления. Тогда из уравнения моментов такого рычага:
F∑пр·hпр=∑Fi·hi, получим: F∑пр=∑Fi·hi/hпр, где hi и hпр – кратчайшие расстояния от полюса плана скоростей до линии действия i-ой и приведенной сил.
Повернутый на 90˚ план скоростей с приложенными к нему силами называется жестким рычагом Жуковского.
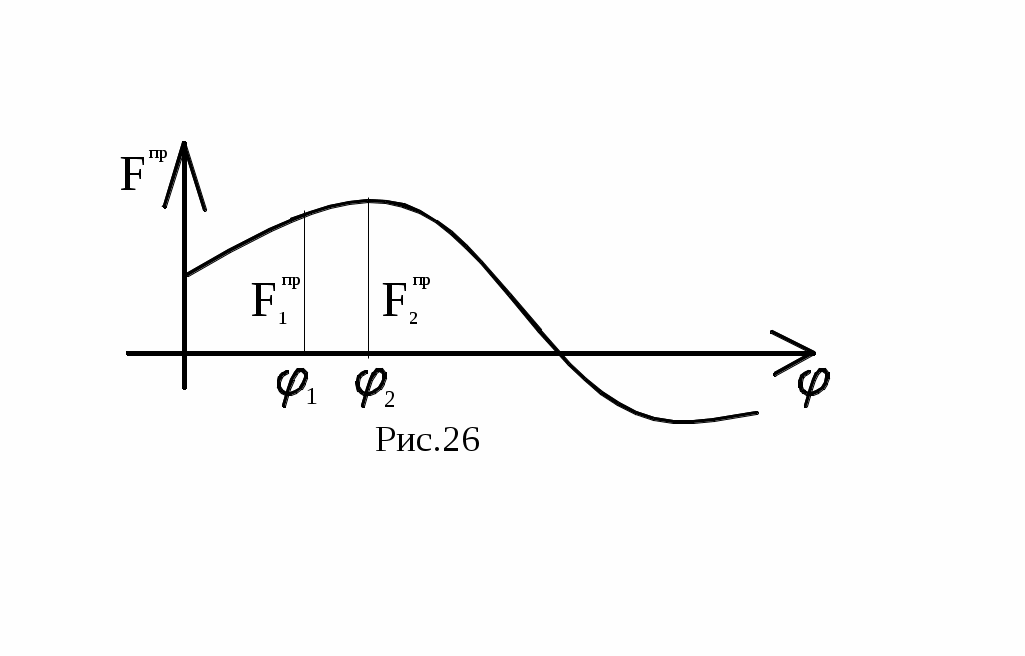
Величина Fпр или Мпр зависит от положения механизма, поэтому можно построить диаграмму, например, Fпр(φ), являющуюся функцией положения звена приведения. Для этого необходимо последовательно определить значения Fпр методом рычага Жуковского для целого ряда положений механизма в пределах цикла (F1пр, F2пр,…) и отложить их на диаграмме (рис.26).
Приведенная сила F∑пр или момент М∑пр характеризует реакцию механизма на движение его входного звена по определенному закону, задаваемому двигателем. Сила или момент, равные по величине приведенной силе или моменту, но противоположные им по направлению называется уравновешенной силой F
ур или моментом Мур. Эта сила или момент развивается двигателем и обеспечивает заданное движение входного звена.
Если к рычагу Жуковского приложить все внешние силы, включая силы инерции, а также Fур, то его можно рассматривать в равновесии, из условия которого: Fур·hур+∑Fi·hi=0 можно определить неизвестную Fур, а также найти мощность двигателя Pдв, требуемую для получения заданного движения входного звена в заданном положении:
Pдв=Fур·VA·cos(FурVA)=Mур·ω.
5.5. Графоаналитический метод решения уравнения движения машины
Данный метод позволяет не только наглядно иллюстрировать связь между динамическими и кинематическими параметрами движения, но и решать практические задачи синтеза, например, задачу уменьшения неравномерности вращения звеньев.
В качестве примера рассмотрим построение так называемой диаграммы энергомасс. Эта диаграмма строится на основе графиков:
∆Тпр(φ)=Тпр(φ)-Т0пр(φ) и Jпр(φ),
причем график ∆Тпр(φ) может быть получен путем графического интегрирования графика Мпр(φ).
На рис.27 показана последовательность построения диаграммы энергомасс в координатах ∆Тпр(Jпр), которая при установившемся движении является замкнутой кривой и строится на базе диаграмм ∆Тпр(φ) и Jпр(φ) путем исключения параметра φ (φ – угол поворота звена приведения).
Если известна угловая скорость вращения ω0 звена приведения в начале цикла, то можно определить начальную кинетическую энергию:Т0пр=1/2·J0пр·ω02.
Тогда диаграмму энергомасс можно рассматривать в координатах Тпр(J1пр), где ось J1пр отстоит от первоначальной оси Jпр на величину Т0пр (рис.27).
Т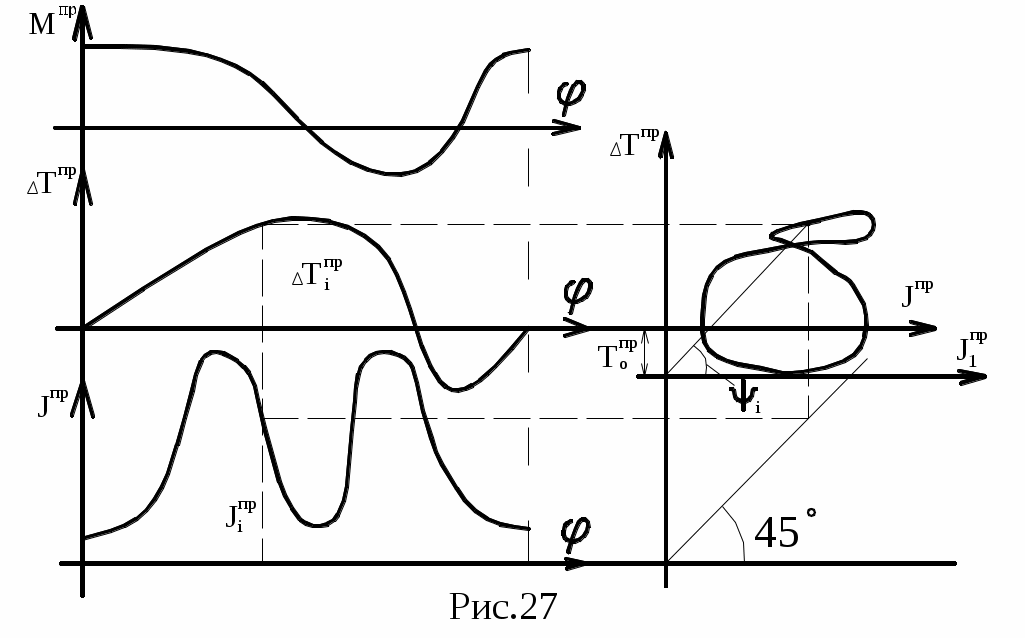
ак как Тпр=1/2·Jпр·ω2, то ω2=2·Тпр/Jпр=2·μТ/μJ·tgΨ,
где μТ и μJ – масштабные коэффициенты, используемые для построения диаграмм. Таким образом, диаграмма энергомасс позволяет при установившемся движении определить угловую скорость ω звена приведения в любой момент времени, т.е.
ω=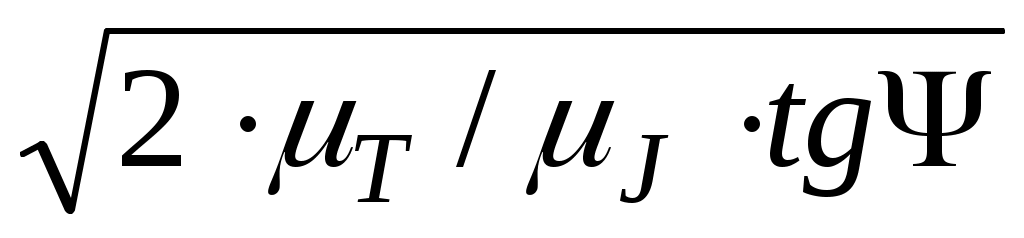 ; а tgΨ= μJ/μT·ω2/2.
; а tgΨ= μJ/μT·ω2/2.
5.6. Неравномерное движение машин. Маховики
 Одним из режимов движения машины при совершении полезной работы является режим равномерного или установившегося движения.
Одним из режимов движения машины при совершении полезной работы является режим равномерного или установившегося движения.
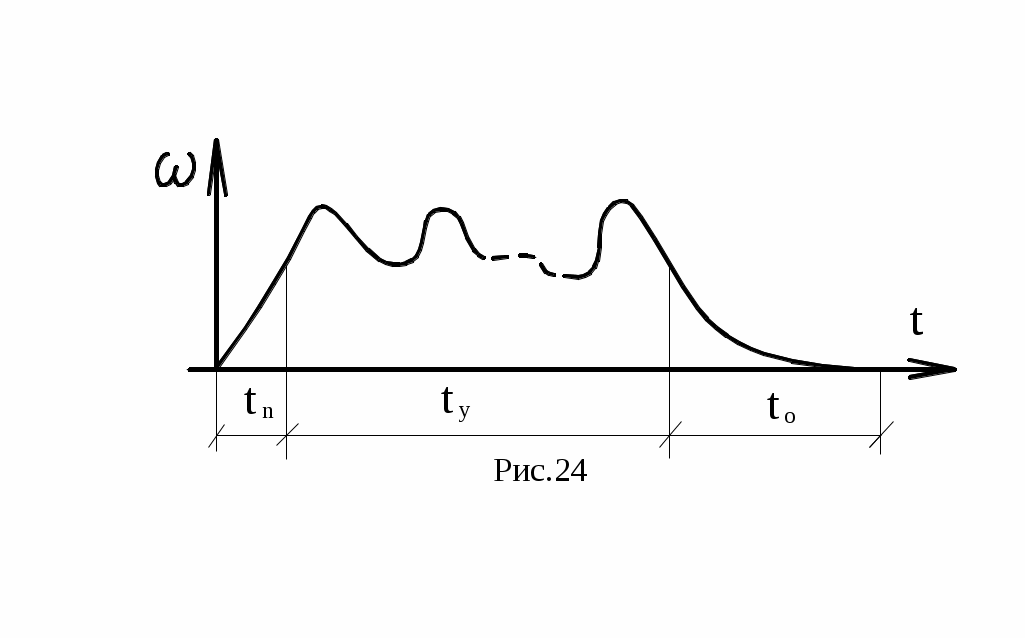
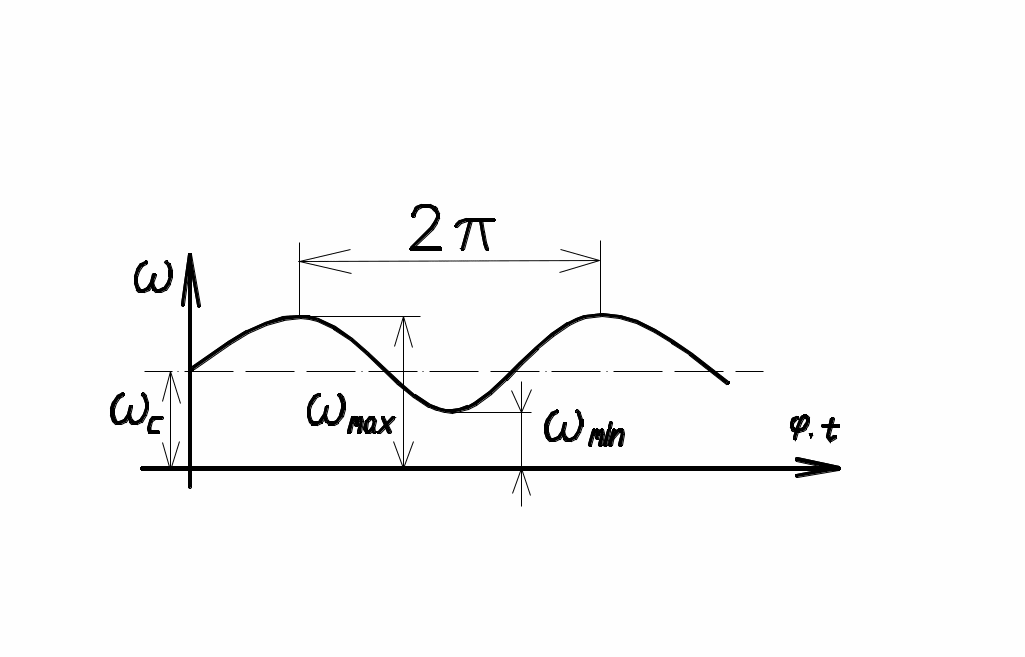
При равномерном движе-нии угловая скорость ω вала двигателя постоянна, а при установившемся движении она
Рис. 28 периодически изменяется (рис.28),
причём степень неравномерности можно оценить коэффициентом неравномерности:
δ=(ωmax- ωmin)/ωc,
где ωс – средняя угловая скорость за цикл ωс=(ωmax+ ωmin)/2.
Неравномерность вредно сказывается на работе машин, т.к. вызывает дополнительные инерционные нагрузки, которые могут привести к поломке.
Практикой установлены значения δ, которые допустимы в различных условиях эксплуатации. Регулировать величину δ можно путем изменения величины момента инерции звена приведения, т.е. на быстро вращающийся вал закрепляется дополнительная масса, называемая маховиком.
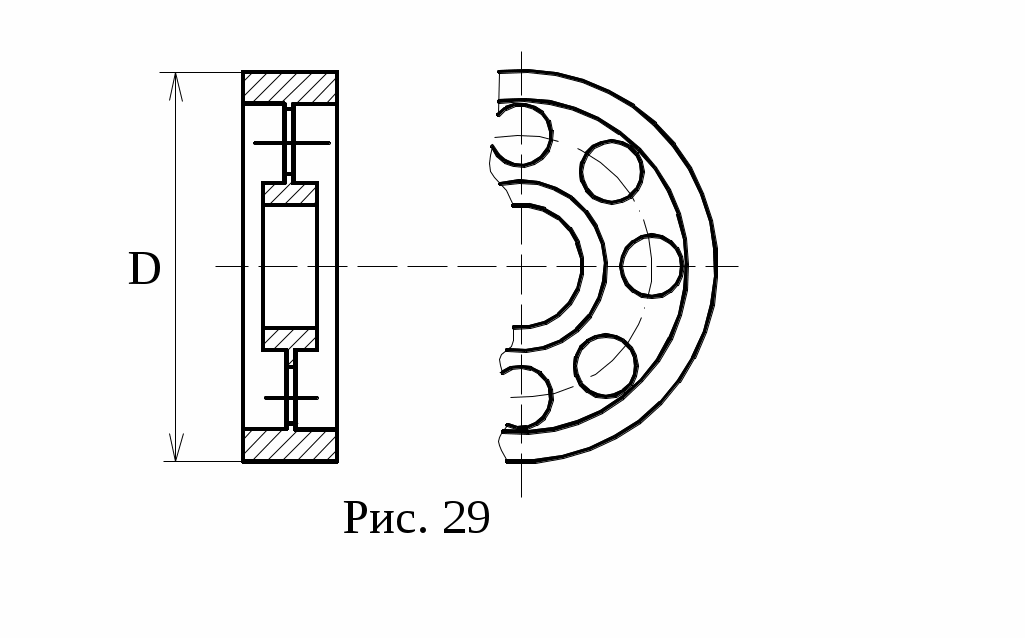 При конструировании маховика стремятся к получению необходимого момента инерции маховика Jм с наименьшим весом G и заданным диаметром D. Для этой цели маховик изготавливается в виде тяжелого обода, соединенного со втулкой тонким диском с отверстием или спицами (рис.29). Приближенно Jм можно определить по формуле:
При конструировании маховика стремятся к получению необходимого момента инерции маховика Jм с наименьшим весом G и заданным диаметром D. Для этой цели маховик изготавливается в виде тяжелого обода, соединенного со втулкой тонким диском с отверстием или спицами (рис.29). Приближенно Jм можно определить по формуле:
Jм≈G·D2/40, кг·м·с2.
5.7. Подбор момента инерции Jм маховика по заданному
коэффициенту неравномерности δ
Обычно требуется определить параметры маховика при заданных значениях ωср и δ. Существует два наиболее распространенных метода определения Jм – Н.И. Мерцалова и метод Ф. Виттенбауэра. Рассмотрим более точный метод Ф. Виттенбауэра, при котором предварительно строится диаграмма энергомасс ∆Тпр(Jпр).
Согласно этой диаграмме (рис.30): ω2max,min=2·μТ/μJ·tgΨmax,min,
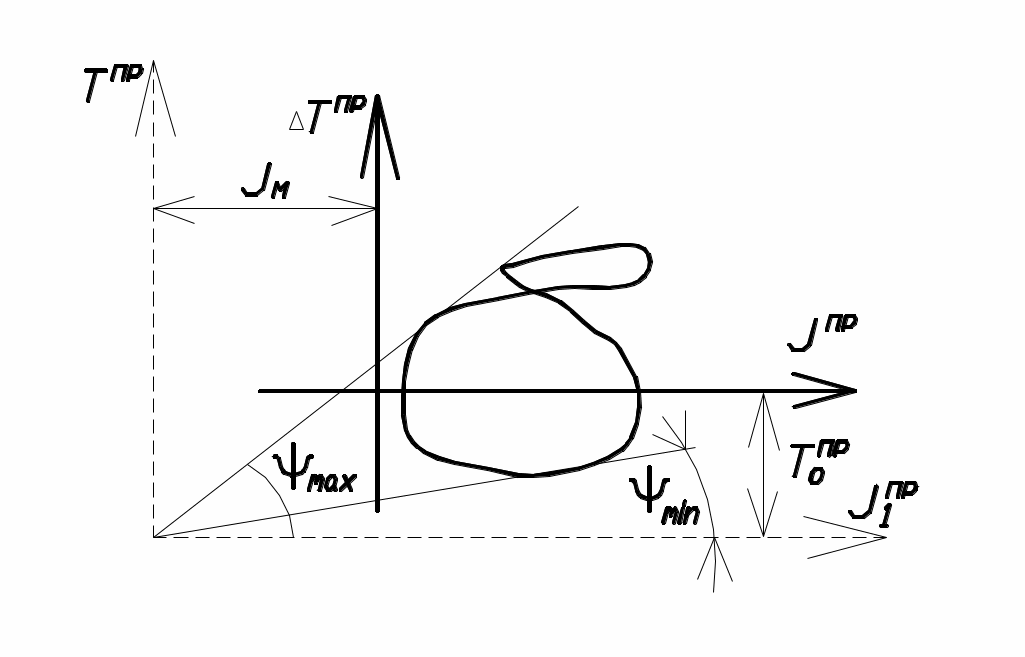 tgΨmax,min= μJ/μT·ω2max
tgΨmax,min= μJ/μT·ω2max
Здесь pb, pc, ps|=ps·cos(G^VS) – вектора, взятые с плана скоростей (рис.22).
Как видно из формул, величина Fпр (Мпр) зависит лишь от соотношения скоростей, а не от их абсолютной величины, что позволяет для приведения сил использовать планы скоростей без учета их масштабов. Каждое i-ое звено механизма обладает массой mi и моментом инерции Ji относительно оси, проходящей через центр масс звена, при этом кинетическая энергия i-го звена плоского механизма равна:
Ti=(mi·Vi2/2)+Ji·ωi2/2.
 Массы и моменты инерции всех звеньев механизма можно условно заменить некоторой массой mпр, сосредоточенной в произвольно выбранной точке А звена приведения (рис.23, а) или некоторым моментом инерции Jпр, приписанным звену
Массы и моменты инерции всех звеньев механизма можно условно заменить некоторой массой mпр, сосредоточенной в произвольно выбранной точке А звена приведения (рис.23, а) или некоторым моментом инерции Jпр, приписанным звену Рис. 23 приведения (рис.23, б).
Замена должна производится из условия равенства кинетических энергий:
Тпр=Тмех=∑Тi,
где Тпр=mпр·VA2/2 или Тпр=Jпр·ω2/2,
т.е. mпр=∑[mi·(Vi/VA)2+Ji·(ωi/VA)2] – при поступательном движении звена приведения.
Jпр=∑[ mi·(Vi/ω)2+Ji·(ωi/ω)2] – при вращательном движении звена приведения.
mпр и Jпр являются функциями положения звена приведения, т.е. их величина может меняться при изменении положения звена в процессе его движения.
5.3. Уравнение движения машины
Работу машины можно разбить на 3 периода:
-
период пуска (разгон); -
период установившегося движения; -
период остановки (выбега);

Аналитическая зависимость между действующими на звенья силами и кинематическими параметрами движения называется уравнением движения. Это уравнение в общем случае имеет вид ∆Т=Ад-Ас, где ∆Т=Т-Т0 – изменение кинетической энергии за рассматриваемый промежуток времени (Т и Т0 – величина кинетической энергии в конце и начале промежутка);
Ад-Ас – суммарная работа действующих сил за рассматриваемый промежуток (Ад, Ас – работа движущих сил и сил сопротивления).
В период пуска Ад-Ас=∆Т>0, т.е. происходит ускорение движения звеньев, являющегося неустановившемся.
В период установившегося движения Ад-Ас=∆Т=0, т.е. скорости звеньев в конечный и начальный моменты цикла равны и вся работа движущихся сил расходуется на преодоление сопротивлений.
В период остановки Ад-Ас=∆Т<0, движение продолжается некоторое время за счет накопленной кинетической энергии, поглощаемой за счет сопротивления движению.
Уравнение движения может быть выражено в интегральной и дифференциальной форме, а для упрощения его решения исследование машины заменяют исследованием звена приведения, в котором изменение кинетической энергии равно: ∆Tпр =Адпр-Аспр, где суммарная работа действующих на звено приведения сил может быть выражена:
а) в интегральной форме:
Адпр-Аспр=∫F∑прds или Адпр-Аспр=∫M∑прdφ;
б) в дифференциальной форме:
dTпр=M∑прdφ или M∑пр=dTпр/dφ;
т.е. при dTпр=1/2·Jпр·ω2 получим:
M∑пр=(dJпр/dφ)·(ω2/2)+Jпр·ω·(dω/dφ)·(dt/dt)=(dJпр/dφ)·(ω2/2)+ε·Jпр.
Таким образом, уравнение движения машины приводится к тому или иному конкретному виду и решается графическим и графоаналитическим методами, а учитываемые силы и моменты сил, а также приведенные массы и моменты инерции могут быть как постоянными так и переменными величинами, зависящими от того или иного фактора.
5.4. Понятие об уравновешивающей силе.
Теорема Жуковского о жестком рычаге
Одним из способов определения приведенной силы Fпр является способ, предложенный проф. Н.Е. Жуковским. Уравнение, из которого может быть найдена Fпр, основано на равенстве мощностей: F∑пр·VA·cos(F∑пр VA)=∑Fi·Vi·cos(Fi Vi).
 Рассмотрим какое-либо звено механизма, в т. В которого приложена сила Fi под углом αi к вектору скорости Vi этой точки (рис.25, а).
Рассмотрим какое-либо звено механизма, в т. В которого приложена сила Fi под углом αi к вектору скорости Vi этой точки (рис.25, а).Мощность силы Fi равна:
Pi=Fi·Vi·cosαi.
Если вектор скорости т. В (план скоростей) повернуть на
Рис. 25 90˚ и силу Fi приложить к концу вектора (в т. «b»), сохранив ее направление, то момент этой силы относительно полюса «p» будет равен (рис.25, б): Mi=Fi·hi=Fi·Vi·cosαi=Pi,
т.е. равен мощности силы Fi. Таким образом, Fi можно найти, повернув на 90˚ план скоростей и приложив к нему все внешние силы, включая силы инерции, в соответствующих точках и сохраняя их направления. Тогда из уравнения моментов такого рычага:
F∑пр·hпр=∑Fi·hi, получим: F∑пр=∑Fi·hi/hпр, где hi и hпр – кратчайшие расстояния от полюса плана скоростей до линии действия i-ой и приведенной сил.
Повернутый на 90˚ план скоростей с приложенными к нему силами называется жестким рычагом Жуковского.
Величина Fпр или Мпр зависит от положения механизма, поэтому можно построить диаграмму, например, Fпр(φ), являющуюся функцией положения звена приведения. Для этого необходимо последовательно определить значения Fпр методом рычага Жуковского для целого ряда положений механизма в пределах цикла (F1пр, F2пр,…) и отложить их на диаграмме (рис.26).

Приведенная сила F∑пр или момент М∑пр характеризует реакцию механизма на движение его входного звена по определенному закону, задаваемому двигателем. Сила или момент, равные по величине приведенной силе или моменту, но противоположные им по направлению называется уравновешенной силой F
ур или моментом Мур. Эта сила или момент развивается двигателем и обеспечивает заданное движение входного звена.
Если к рычагу Жуковского приложить все внешние силы, включая силы инерции, а также Fур, то его можно рассматривать в равновесии, из условия которого: Fур·hур+∑Fi·hi=0 можно определить неизвестную Fур, а также найти мощность двигателя Pдв, требуемую для получения заданного движения входного звена в заданном положении:
Pдв=Fур·VA·cos(FурVA)=Mур·ω.
5.5. Графоаналитический метод решения уравнения движения машины
Данный метод позволяет не только наглядно иллюстрировать связь между динамическими и кинематическими параметрами движения, но и решать практические задачи синтеза, например, задачу уменьшения неравномерности вращения звеньев.
В качестве примера рассмотрим построение так называемой диаграммы энергомасс. Эта диаграмма строится на основе графиков:
∆Тпр(φ)=Тпр(φ)-Т0пр(φ) и Jпр(φ),
причем график ∆Тпр(φ) может быть получен путем графического интегрирования графика Мпр(φ).
На рис.27 показана последовательность построения диаграммы энергомасс в координатах ∆Тпр(Jпр), которая при установившемся движении является замкнутой кривой и строится на базе диаграмм ∆Тпр(φ) и Jпр(φ) путем исключения параметра φ (φ – угол поворота звена приведения).
Если известна угловая скорость вращения ω0 звена приведения в начале цикла, то можно определить начальную кинетическую энергию:Т0пр=1/2·J0пр·ω02.
Тогда диаграмму энергомасс можно рассматривать в координатах Тпр(J1пр), где ось J1пр отстоит от первоначальной оси Jпр на величину Т0пр (рис.27).
Т

ак как Тпр=1/2·Jпр·ω2, то ω2=2·Тпр/Jпр=2·μТ/μJ·tgΨ,
где μТ и μJ – масштабные коэффициенты, используемые для построения диаграмм. Таким образом, диаграмма энергомасс позволяет при установившемся движении определить угловую скорость ω звена приведения в любой момент времени, т.е.
ω=
5.6. Неравномерное движение машин. Маховики
 Одним из режимов движения машины при совершении полезной работы является режим равномерного или установившегося движения.
Одним из режимов движения машины при совершении полезной работы является режим равномерного или установившегося движения.При равномерном движе-нии угловая скорость ω вала двигателя постоянна, а при установившемся движении она
Рис. 28 периодически изменяется (рис.28),
причём степень неравномерности можно оценить коэффициентом неравномерности:
δ=(ωmax- ωmin)/ωc,
где ωс – средняя угловая скорость за цикл ωс=(ωmax+ ωmin)/2.
Неравномерность вредно сказывается на работе машин, т.к. вызывает дополнительные инерционные нагрузки, которые могут привести к поломке.
Практикой установлены значения δ, которые допустимы в различных условиях эксплуатации. Регулировать величину δ можно путем изменения величины момента инерции звена приведения, т.е. на быстро вращающийся вал закрепляется дополнительная масса, называемая маховиком.
 При конструировании маховика стремятся к получению необходимого момента инерции маховика Jм с наименьшим весом G и заданным диаметром D. Для этой цели маховик изготавливается в виде тяжелого обода, соединенного со втулкой тонким диском с отверстием или спицами (рис.29). Приближенно Jм можно определить по формуле:
При конструировании маховика стремятся к получению необходимого момента инерции маховика Jм с наименьшим весом G и заданным диаметром D. Для этой цели маховик изготавливается в виде тяжелого обода, соединенного со втулкой тонким диском с отверстием или спицами (рис.29). Приближенно Jм можно определить по формуле: Jм≈G·D2/40, кг·м·с2.
5.7. Подбор момента инерции Jм маховика по заданному
коэффициенту неравномерности δ
Обычно требуется определить параметры маховика при заданных значениях ωср и δ. Существует два наиболее распространенных метода определения Jм – Н.И. Мерцалова и метод Ф. Виттенбауэра. Рассмотрим более точный метод Ф. Виттенбауэра, при котором предварительно строится диаграмма энергомасс ∆Тпр(Jпр).
Согласно этой диаграмме (рис.30): ω2max,min=2·μТ/μJ·tgΨmax,min,
 tgΨmax,min= μJ/μT·ω2max
tgΨmax,min= μJ/μT·ω2max