ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 266
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6.4.7 Метод угла отсечки используется для гармонического анализа при аппроксимации характеристики нелинейного элемента ломаной линией (рисунок 6.3). Какой параметр ломанной линии и определяет нелинейные свойства данной цепи?
6.4.8 Определить условия нелинейного преобразования входного сигнала с учетом напряжения смещения, напряжения отсечки и амплитуды входного гармонического сигнала.
6.4.9 На основании определения угла отсечки, рассчитать угол отсечки неискаженного гармонического сигнала.
6.4.10 Дать определение оптимального угла отсечки для k – гармоники.
6.4.11 Определить по рисунку 6.6 углы отсечки для фрагментов 1, 2, 3.
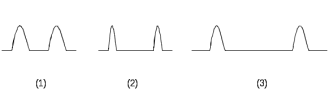
Рис.6.6 – Примеры выходного сигнала при прохождении нелинейной цепи, аппроксимированной ломаной прямой
6.4.11 Определить угол отсечки для максимизации амплитуды 3-й гармоники.
6.4.12 Определить напряжение отсечки нелинейного преобразователя, если угол отсечки равен 90о, а напряжение смещения равно 2 В.
6.4.13 Нелинейный преобразователь представлен полиномом L2(x) = a0 + a1x + a2x2 на вход которого поступает сигнал s1(t)=A(t)cos(105t + φ) и вспомогательный сигналs2(t) = А1cos(ω0t + φ). Определить частоту ω0, если сигнал s1(t) надо переместить на частоту равной 106 рад/сек.
6.4.14 Определить амплитуду тока удвоенной частоты на выходе умножителя, если угол отсечки соответствует оптимальному режиму, а S = 20 mA/B, U = 3 B.
6.4.15 Определить коэффициент нелинейных искажений Кнумножителя для n=3, на выходе которого установлен колебательный контур с добротностью Q= 20 для оптимального угла отсечки. Коэффициент Кн определяется как:
Кн = (U1 +U2)/U3,
где U1 - амплитуда 1 – й гармоники, U2 - амплитуда 2-й гармоники, а U3 - 3 – й гармоники.
6.4.16. Построить зависимость максимальной величины коэффициентов Берга от угла отсечки, воспользовавшись рисунком 6.7.
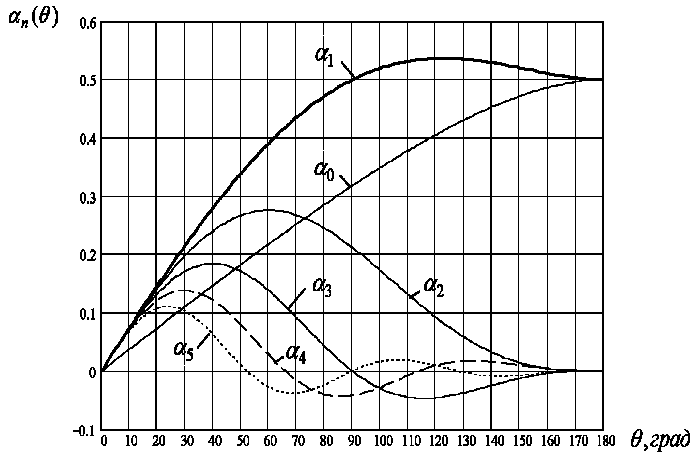
Рис. 6.7 – Графики функций αn(θ).
7 Радиотехнические устройства для формирования модулированных сигналов
7.1 Устройства формирования и детектирования сигналов с амплитудной модуляцией.
7.1.1 Модуляторы АМ- сигналов
Устройство модуляции АМ-сигнала строится в соответствии с формулой (3.6), из которой следует, что оно является произведением двух сигналов и, следовательно, для получения необходимо перемножить два сигнала. Рассмотрим способы, основанные на использовании нелинейных элементах.
На рисунке 7.1 приведена схема модулятора АМ на диоде с квадратической характеристикой.
Рис.7.1- Принципиальная схема модулятора АМ колебаний с использованием нелинейного элемента – диода с квадратичной характеристикойПроведем математический анализ для случая модуляции одним тоном.
Пусть uω (t) = Uωcosω0t и uΩ (t) = U0 +kS(t), тогда
u = uω + uΩ = Uωcosω0t + U0 +kS(t)
i = au2 = auω2 +auΩ2 + 2aUω[U0 + kS(t)]cosω0t.
Последнее слагаемое, является удвоенным произведением uωuΩ и представляет собой АМ-сигнал.
Если S(t) = UΩcosΩt, то 2аuωuΩ, = 2аUωU0[1 + (kUΩ/U0)cosΩt]cosω0tили
аuωuΩ, = Uω0 (1 + mcosΩt)cosω0t, где
Uω0 = аUωU0 ; m = kUΩ/U0.
В рассмотренной схеме модуляции предполагалось, что характеристика нелинейного элемента – квадратичная. Характеристики реальных элементов отличаются от квадратичных. Проведем математический анализ с учетом этого обстоятельства.
Представим нелинейный оператор в общем виде:
L(x) = a0 + a1( x1 +x2 ) + a2 (x1 + x2)2 + a3 (x1 + x2)3 + . . .
Вводя значения х1 = UΩcosΩt; x2 = Uωcosω0t, находим
L(x) = a0 + a1UΩ cos Ωt + a1Uω cos ω0t + a2UΩ2 cos2 Ωt + a2Uω2 cos2 ω0 t +
a2 2UΩ Uω cosΩt cos ω0 t + a3 UΩ3 cos3 Ωt + a3 Uω3 cos3 ω0 t +
a3 3UΩ2 Uω cos2 Ωt cos ω0 t + a3 3UΩ Uω2 cos Ωt cos2 ω0 t
Группируя члены этого выражения, содержащие колебания различных частот, получаем [4]:
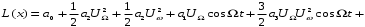
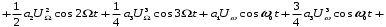
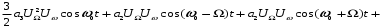
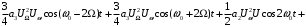
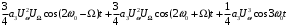
Нагрузка – параллельный колебательный контур – отфильтровывает составляющие с частотами, близкими к его резонансной частоте ωр.
Сохраним в записи только те составляющие, которые останутся после фильтрации, записав их в следующем виде;
+
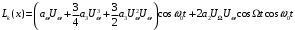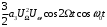.Введем обозначение
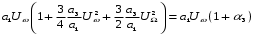
и перепишем выражение для Lk(x):
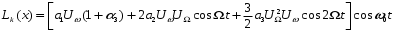Последнему выражению целесообразно придать следующую форму:
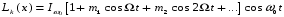,где
;
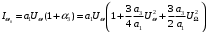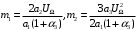.Аналогично можно подсчитать m3 и так далее.
Проведем упрощенный анализ модулятора АМ-колебания, принципиальная схема которого показана на рисунке 7.2. На вход затвора транзистора подается напряжение:
uз = Eсм + UΩcosΩt + Uωcosω0t.
Аппроксимируя характеристику транзистора полиномом второй степени ic = a0 + a1uз + a2uз2 и подставляя значение uз в выражение для тока стока ic, находим ic (t):
i (t) = a0 + a1 (Eсм + UΩcos Ω t + Uωcos ω0t ) + a2 (Eсм + UΩ cos Ωt + Uω cos ω0t)2
a0 + a1Eсм + a1UΩ cos Ω t + a1 Uω cos ω0t + a2 Eсм2 + a2 UΩ2cos2Ω t +
a2 Uω2cos2 ω0 t + 2a2 Eсм UΩ cos Ω t + 2 a2 Eсм Uωcos ω0t +
2a2 UΩ Uω cos ω0t cos Ω t
Определим напряжение на выходе модулятора. Контур настроен на частоту ω0 и представляет для колебания этой частоты сопротивление Rэ0. Для простоты примем, что сопротивление контура для колебаний частот, близких к резонансной, также равно Rэ0. Тогда напряжение на выходе:
=
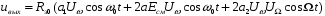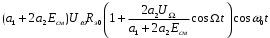
Приняв
, 
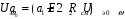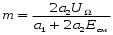
получим
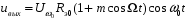
Рис.7.2 – Принципиальная схема модулятора АМ-сигнала на транзисторе
Для выбора правильного режима схемы и оценки качества модуляции снимают (или рассчитывают) статическую характеристику модуляционную характеристику, которая является целевой функцией – основной характеристикой модуляционного устройства. Она представляет собой зависимость амплитуды первой гармоники тока I1 от напряжения смещения Eсм (при постоянной амплитуде напряжения высокой частоты Uω ), то есть,
I
1 = f(Eсм) при Uω =const.
Рассчитаем статическую модуляционную характеристику для случая аппроксимации транзистора полиномом третей степени:
I1 = a0 + a1(uз ) + a2 (uз )2 + a3 (uз )3 ,
Подставляявыражение:uз = Eсм + Uωcosω0tв формулу выше, получаем:
I1 = f(Eсм), а именно:
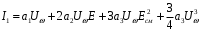
Как видно из этого выражения, последнее слагаемоеприводит к нелинейности модуляционной характеристики [5].
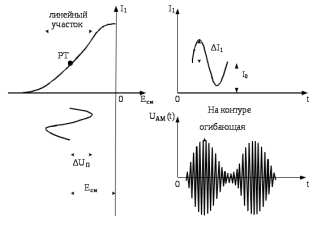
Рис.7.3 – Статистическая модуляционная характеристика с заданным режимом работы и допустимыми значениями напряжений для получения неискаженной амплитудной модуляции сигнала
На рисунке 7.3 приведена статическая модуляционная характеристика. По статической модуляционной характеристике можно определить линейный участок, а затем выбрать начальное напряжение смещения Есм0 и наибольшую амплитуду модулирующего сигнала UΩмакс.
Как показано на рисунке 7.3 рабочая точка выбирается в середине линейного участка статической модуляционной характеристики и определяется напряжение смещение Есм. Далее определяется максимальное значение модулирующего сигнала неискаженной модуляции на основе выражения:
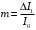
где I0– соответствует UΩ = 0.
На рисунке 7.4 приведены временные диаграммы АМ-сигнала при смещении рабочей точки.
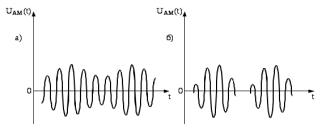
Рис.7.4 – Временные диаграммы АМ-сигнала при искажении сверху (а) – рабочая точка смещена вправо и при искажении снизу (б) – рабочая точка смещена влево.
Из рассмотрения построения статической модуляционной характеристики, можно сделать вывод, что она полностью определяет возможности получения неискаженной модуляции.
7.1.2 Устройства детектирования АМ- сигналов
Принятое высокочастотной колебание после отделения от других сигналов и усиления необходимо преобразовать в колебание низкой частоты, то есть в тот видеосигнал, которым осуществлялась модуляция. Таким образом, задача детектирования АМ колебаний состоит в измерение текущей амплитуды