ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 260
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
модуляции [6].
Рассмотрим перенос спектра сигнала в область высоких частот. Предварительно в передатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебанием. Его математическая модель u(t) = f(t; a1 ,a2 ,a3 , . . . . am ) такова, что имеется некоторая совокупность параметров a1 ,a2 ,a3 , . . . . am, определяющих форму этого колебания. Итак , S(t) - низкочастотное сообщение, подлежащее передаче по радиоканалу. Пусть хоть один из указанных параметров изменяется во времени по закону передаваемого сообщения, то несущее колебание приобретает новое свойство – оно несет в себе информацию, которая первоначально была заключена в сигнале S(t).
Физический процесс управления параметрами несущего колебания и является модуляцией.
Амплитудная модуляция в свое время получила широкое распространение, которая использует в качестве несущего сигнала, простое гармоническое колебание (гармонический переносчик информации):
Uг (t) = Ucos(ωt+φ),
имеющие три свободных параметра U, ω, φ.
Изменяя по закону модулирующего сигнала, любой из перечисленных параметров, можно получать различные виды модуляции.
Если параметров окажется амплитуда сигнала U(t), причем остальные параметра ω и φ неизменны, то имеется амплитудная модуляция несущего колебания. Форма записи амплитудно-модулированного, или АМ-сигнала, такова:
uАМ (t) = U(t)cos(ω0t+φ0).
На рисунке 3.1 представлены временные зависимости модулирующего сигнала и АМ- сигнала
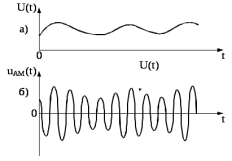
Рис. 3.1 – Формирование АМ - сигнала, а) модулирующий сигнал, б) АМ - сигнал
Задача создания амплитудно-модулированных (АМ) колебаний формулируется следующим образом: имеется высокочастотное колебание (созданное генератором)
uг (t) = Uгcosω0t
и «медленно меняющиеся» колебание Ω << ω
uΩ (t) = U0 +kS(t) (3.1)
требуется получить колебание с переменной амплитудой
uАМ (t) = [Uω + bS(t)]cosω0 t (3.2)
В выражениях (3.10) и (3.2) k и b – коэффициенты пропорциональности, S(t) сигнал, который содержит информацию.
Простейшим модулирующим сигналом служит гармоническое колебание (так называемая модуляция одним тоном):
S(t) = UΩcosΩt (3.3)
Подставляя (3.3) в (3.2), получаем:
UАМ (t) = (Uω + bUΩcosΩt)cosω0t(3.4)
Отношение максимального изменения амплитуды модулированного высокочастотного сигнала к амплитуде немодулированного колебания (рисунок 3.2) называется коэффициентом модуляции или глубиной модуляции и обозначается символом [7]:
m =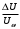
(3.5)
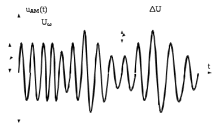
Рис. 3.2 – Эпюры напряжения АМ- сигнала при модуляции одним тоном
С учетом обозначения (3.5) выражение для АМ - колебания записывается обычно в виде:
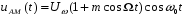(3.6)
Коэффициент модуляции m в общем случае является функцией времени и может изменяться в пределах 0< m <1.
Модулированное колебание даже при модуляции простейшим гармоническим сигналов является сложным и представляет собой ряд элементарных гармонических колебаний. Найдем его спектр, раскрыв скобки в выражении (3.6):
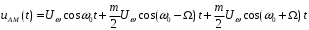
Соответствующая спектрограмма изображена на рисунке 3.3. Частота ω называется несущей, а частоты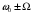
боковыми частотами модулирующего колебания.
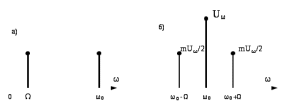
Рис.3.3 – Спектры колебаний до модуляции (а) и после модуляции (б)
При модуляции сложным сигналом, представляющим собой, например, сумму гармонических составляющих, модулированное колебание записывается в виде:
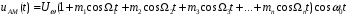
Коэффициенты mj называются парциальными или частичными коэффициентами модуляции. Для этих коэффициентов должно выполняться неравенство: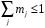
.
Рассмотрим энергетические характеристики при модуляции одним гармоническим сигналом. Усредним выражение (3.6) за период высокой частоты ω, при этом учтем, что ω >> Ω, получим среднее значение мощности АМ - сигнала:
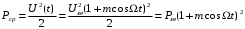
При возведении в квадрат, необходимо учитывать, что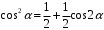
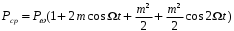(3.7)
где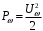
- мощность колебания несущей частоты.
Как следует из выражения (3.7), мощность может меняться от 0, при Ωt=π и до максимального выражения, равного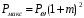
при Ωt=0, 2π, если m≈1.
Таким образом, при 100%-ной модуляции ( m=1), мощность может изменяться в пределах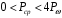
и передатчик должен развивать мощность, вчетверо превышающую мощность Рω на несущей частоте.
Среднее значение мощности РсрΩза период низкой частоты, как следует из выражения (3.7):
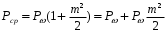(3.8)
где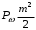
- мощность двух колебаний боковых частот.
Равенство (3.8) показывает, что при 100% -ной модуляции, 66,6% всей колебательной мощности передатчика затрачивается на передачу колебания несущей частоты и только 33,3% мощности приходится на оба колебания боковых частот.
3.2 Частотная модуляция
Частотной модуляцией называется такая модуляция, где мгновенная частота гармонического сигнала изменяется по закону модулирующего сигнала.
Пусть высокочастотное колебание генератора представлено как:
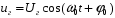, (3.9)
где полная фаза колебаний ψ = ω0t + φ0 линейно изменяется во времени.
Представим (3.9) как: u = Ucos[ψ(t)], где изменение фазы происходит в результате модуляции мгновенной частоты сигналов S(t), то есть :
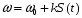
При модуляции моногармоническим сигналом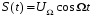
, мгновенная частота: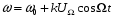 
Максимальное изменение частоты называется девиацией частоты и обозначается как Δω: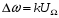
;
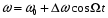. (3.10)
Так как частота есть скорость изменения фазы колебания, фаза находится путем интегрирования (3.10). Таким образом, получаем:
.
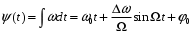В последнем выражении φ0 - начальная фаза без потери общности, может быть приравнена нулю.
Выражение для ЧМ при модуляции чистым тоном, таким образом, принимает вид:
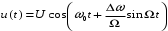
Здесь U - амплитуда немодулированного колебания; ω0 – несущая, а точнее центральная частота.
Максимальное отклонение фазы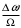
называется индексом частотной модуляции и обозначается символом Мч:
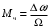
Простейшее ЧМ колебание, следовательно, записывается в виде:
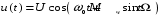(3.11)
Рассмотрим спектральное представление ЧМ сигнала. Перепишем выражение (3.11), воспользовавшись равенством
cos(α+β) = cos α cos β - sin α sin β, в следующем виде:
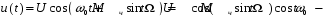
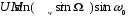(3.12)
Пусть Мч<<1 . При этом имеют место следующие приближенные равенства [8]:
Cos(Mч sinΩt) ≈ 1 и sin(Mч sinΩt) ≈ Mч sinΩt;
При подстановки в формулу (3.12) получаем:
=
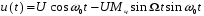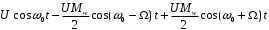(3.13)
При малом индексе модуляции амплитудный спектр простейшего ЧМ колебания практически не отличается от спектра простейшего АМ колебания, то есть при модуляции одним тоном спектр состоит из трех составляющих: колебание несущей частоты и двух колебаний боковых частот.
Частотная модуляция при малых индексах модуляции обладает низкой помехоустойчивостью и не применяется в радиотехнике. Наибольший интерес вызывает частотная модуляция при больших индексах модуляции.
Выражение (3.12) можно представить как два АМ колебания:
,
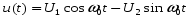где огибающие U1 (t) и U2 (t) равны:
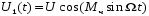и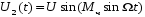 
Так как эти огибающие являются периодическими функциями ( с периодом (ТΩ = 2π/Ω), то для получения их спектра, по которому далее уже не составляет труда найти спектр высокочастотного ЧМ колебания, следовало воспользоваться известными
формулами для разложения в ряд Фурье
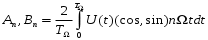
Опуская дальнейшие выкладки по расчету спектра, и ссылаясь на [4], получаем выражение для ЧМ сигнала:
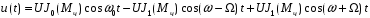
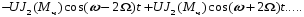
где Jn(Mч) – функция Бесселя первого рода n - го порядка от аргумента Мч (рисунок 3.4).
Рис.3.4 – Функции Бесселя для различных индексов частотной модуляции
Таким образом, спектр ЧМ колебания состоит из несущего колебания с частотой ω0 и амплитудой UJ0 (Mч ) и бесконечного ряда боковых колебаний, с частотами (ω0 ±nΩ) и амплитудами UJn(Mч ).
Следует отметить, что в отличие от амплитудной модуляции, здесь амплитуда колебания несущей частоты UJ0(Mч) может быть сколько малой, и при значении Мч =2,405, может равняться нулю. Амплитуды колебаний боковых частот могут быть больше амплитуды колебания несущей частоты; с каждой стороны несущей имеет место один максимум, как показано на рисунке 3.5.
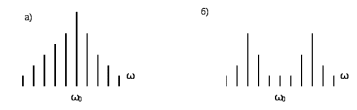
Рис.3.5 – Спектры ЧМ сигнала при а) M ч< 1, б) Мч > 1
При модуляции полигармоническим сигналом, спектр оказывается более сложным. Кроме составляющих (ω0±nΩ),появляются, появляются комбинационные колебания с частотами (ω0±nΩ1 ±nΩ2 ±nΩ3 ±nΩ4…..). Амплитуды составляющих определяются произведением функций Бесселя от индекса модуляции модулирующих сигналов. Например, амплитуда составляющей с частотой[ω0±(nΩ1 ±mΩ2)] равна UJn(Mч1)Jm(Mч2), где Mч1= Δω/Ω1, а Mч2= Δω/Ω2.
Спектр ЧМ сигнала теоретически безграничен, но на практике его ограничивают исходя из-за того, что меньше поступает помех на вход приемного устройства, но при этом происходит искажение сигнала. Таким образом, лавируют между двумя противоречиями. Нормы искажений устанавливаются экспериментально в зависимости от назначения системы связи и свойств получателя сообщения (человек, измерительная аппаратура и т.п.). Эти нормы выражают через амплитуды боковых составляющих, начиная с которых, можно ограничивать спектр. Таким образом, под шириной спектра ЧМ
Рассмотрим перенос спектра сигнала в область высоких частот. Предварительно в передатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебанием. Его математическая модель u(t) = f(t; a1 ,a2 ,a3 , . . . . am ) такова, что имеется некоторая совокупность параметров a1 ,a2 ,a3 , . . . . am, определяющих форму этого колебания. Итак , S(t) - низкочастотное сообщение, подлежащее передаче по радиоканалу. Пусть хоть один из указанных параметров изменяется во времени по закону передаваемого сообщения, то несущее колебание приобретает новое свойство – оно несет в себе информацию, которая первоначально была заключена в сигнале S(t).
Физический процесс управления параметрами несущего колебания и является модуляцией.
Амплитудная модуляция в свое время получила широкое распространение, которая использует в качестве несущего сигнала, простое гармоническое колебание (гармонический переносчик информации):
Uг (t) = Ucos(ωt+φ),
имеющие три свободных параметра U, ω, φ.
Изменяя по закону модулирующего сигнала, любой из перечисленных параметров, можно получать различные виды модуляции.
Если параметров окажется амплитуда сигнала U(t), причем остальные параметра ω и φ неизменны, то имеется амплитудная модуляция несущего колебания. Форма записи амплитудно-модулированного, или АМ-сигнала, такова:
uАМ (t) = U(t)cos(ω0t+φ0).
На рисунке 3.1 представлены временные зависимости модулирующего сигнала и АМ- сигнала
Рис. 3.1 – Формирование АМ - сигнала, а) модулирующий сигнал, б) АМ - сигнал
Задача создания амплитудно-модулированных (АМ) колебаний формулируется следующим образом: имеется высокочастотное колебание (созданное генератором)
uг (t) = Uгcosω0t
и «медленно меняющиеся» колебание Ω << ω
uΩ (t) = U0 +kS(t) (3.1)
требуется получить колебание с переменной амплитудой
uАМ (t) = [Uω + bS(t)]cosω0 t (3.2)
В выражениях (3.10) и (3.2) k и b – коэффициенты пропорциональности, S(t) сигнал, который содержит информацию.
Простейшим модулирующим сигналом служит гармоническое колебание (так называемая модуляция одним тоном):
S(t) = UΩcosΩt (3.3)
Подставляя (3.3) в (3.2), получаем:
UАМ (t) = (Uω + bUΩcosΩt)cosω0t(3.4)
Отношение максимального изменения амплитуды модулированного высокочастотного сигнала к амплитуде немодулированного колебания (рисунок 3.2) называется коэффициентом модуляции или глубиной модуляции и обозначается символом [7]:
m =
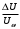(3.5) Рис. 3.2 – Эпюры напряжения АМ- сигнала при модуляции одним тоном
С учетом обозначения (3.5) выражение для АМ - колебания записывается обычно в виде:
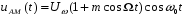(3.6)Коэффициент модуляции m в общем случае является функцией времени и может изменяться в пределах 0< m <1.
Модулированное колебание даже при модуляции простейшим гармоническим сигналов является сложным и представляет собой ряд элементарных гармонических колебаний. Найдем его спектр, раскрыв скобки в выражении (3.6):
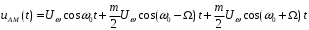
Соответствующая спектрограмма изображена на рисунке 3.3. Частота ω называется несущей, а частоты
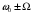боковыми частотами модулирующего колебания. Рис.3.3 – Спектры колебаний до модуляции (а) и после модуляции (б)
При модуляции сложным сигналом, представляющим собой, например, сумму гармонических составляющих, модулированное колебание записывается в виде:
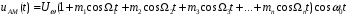
Коэффициенты mj называются парциальными или частичными коэффициентами модуляции. Для этих коэффициентов должно выполняться неравенство:
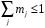. Рассмотрим энергетические характеристики при модуляции одним гармоническим сигналом. Усредним выражение (3.6) за период высокой частоты ω, при этом учтем, что ω >> Ω, получим среднее значение мощности АМ - сигнала:
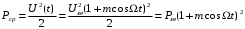
При возведении в квадрат, необходимо учитывать, что
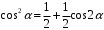
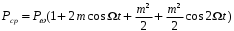(3.7)где
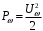- мощность колебания несущей частоты.Как следует из выражения (3.7), мощность может меняться от 0, при Ωt=π и до максимального выражения, равного
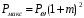при Ωt=0, 2π, если m≈1.Таким образом, при 100%-ной модуляции ( m=1), мощность может изменяться в пределах
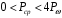и передатчик должен развивать мощность, вчетверо превышающую мощность Рω на несущей частоте.Среднее значение мощности РсрΩза период низкой частоты, как следует из выражения (3.7):
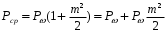(3.8)где
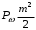- мощность двух колебаний боковых частот.Равенство (3.8) показывает, что при 100% -ной модуляции, 66,6% всей колебательной мощности передатчика затрачивается на передачу колебания несущей частоты и только 33,3% мощности приходится на оба колебания боковых частот.
3.2 Частотная модуляция
Частотной модуляцией называется такая модуляция, где мгновенная частота гармонического сигнала изменяется по закону модулирующего сигнала.
Пусть высокочастотное колебание генератора представлено как:
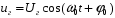, (3.9)где полная фаза колебаний ψ = ω0t + φ0 линейно изменяется во времени.
Представим (3.9) как: u = Ucos[ψ(t)], где изменение фазы происходит в результате модуляции мгновенной частоты сигналов S(t), то есть :
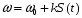
При модуляции моногармоническим сигналом
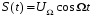, мгновенная частота: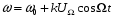 Максимальное изменение частоты называется девиацией частоты и обозначается как Δω:
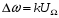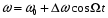; . (3.10)Так как частота есть скорость изменения фазы колебания, фаза находится путем интегрирования (3.10). Таким образом, получаем:
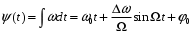.В последнем выражении φ0 - начальная фаза без потери общности, может быть приравнена нулю.
Выражение для ЧМ при модуляции чистым тоном, таким образом, принимает вид:
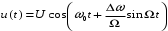
Здесь U - амплитуда немодулированного колебания; ω0 – несущая, а точнее центральная частота.
Максимальное отклонение фазы
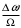называется индексом частотной модуляции и обозначается символом Мч: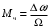 Простейшее ЧМ колебание, следовательно, записывается в виде:
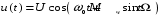(3.11)Рассмотрим спектральное представление ЧМ сигнала. Перепишем выражение (3.11), воспользовавшись равенством
cos(α+β) = cos α cos β - sin α sin β, в следующем виде:
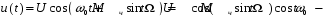
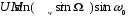(3.12)Пусть Мч<<1 . При этом имеют место следующие приближенные равенства [8]:
Cos(Mч sinΩt) ≈ 1 и sin(Mч sinΩt) ≈ Mч sinΩt;
При подстановки в формулу (3.12) получаем:
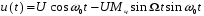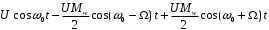= (3.13)При малом индексе модуляции амплитудный спектр простейшего ЧМ колебания практически не отличается от спектра простейшего АМ колебания, то есть при модуляции одним тоном спектр состоит из трех составляющих: колебание несущей частоты и двух колебаний боковых частот.
Частотная модуляция при малых индексах модуляции обладает низкой помехоустойчивостью и не применяется в радиотехнике. Наибольший интерес вызывает частотная модуляция при больших индексах модуляции.
Выражение (3.12) можно представить как два АМ колебания:
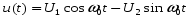,где огибающие U1 (t) и U2 (t) равны:
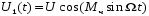и 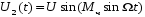Так как эти огибающие являются периодическими функциями ( с периодом (ТΩ = 2π/Ω), то для получения их спектра, по которому далее уже не составляет труда найти спектр высокочастотного ЧМ колебания, следовало воспользоваться известными
формулами для разложения в ряд Фурье
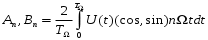
Опуская дальнейшие выкладки по расчету спектра, и ссылаясь на [4], получаем выражение для ЧМ сигнала:
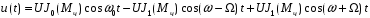
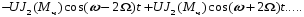
где Jn(Mч) – функция Бесселя первого рода n - го порядка от аргумента Мч (рисунок 3.4).
Рис.3.4 – Функции Бесселя для различных индексов частотной модуляции
Таким образом, спектр ЧМ колебания состоит из несущего колебания с частотой ω0 и амплитудой UJ0 (Mч ) и бесконечного ряда боковых колебаний, с частотами (ω0 ±nΩ) и амплитудами UJn(Mч ).
Следует отметить, что в отличие от амплитудной модуляции, здесь амплитуда колебания несущей частоты UJ0(Mч) может быть сколько малой, и при значении Мч =2,405, может равняться нулю. Амплитуды колебаний боковых частот могут быть больше амплитуды колебания несущей частоты; с каждой стороны несущей имеет место один максимум, как показано на рисунке 3.5.
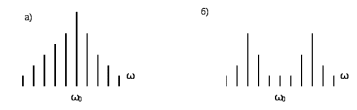
Рис.3.5 – Спектры ЧМ сигнала при а) M ч< 1, б) Мч > 1
При модуляции полигармоническим сигналом, спектр оказывается более сложным. Кроме составляющих (ω0±nΩ),появляются, появляются комбинационные колебания с частотами (ω0±nΩ1 ±nΩ2 ±nΩ3 ±nΩ4…..). Амплитуды составляющих определяются произведением функций Бесселя от индекса модуляции модулирующих сигналов. Например, амплитуда составляющей с частотой[ω0±(nΩ1 ±mΩ2)] равна UJn(Mч1)Jm(Mч2), где Mч1= Δω/Ω1, а Mч2= Δω/Ω2.
Спектр ЧМ сигнала теоретически безграничен, но на практике его ограничивают исходя из-за того, что меньше поступает помех на вход приемного устройства, но при этом происходит искажение сигнала. Таким образом, лавируют между двумя противоречиями. Нормы искажений устанавливаются экспериментально в зависимости от назначения системы связи и свойств получателя сообщения (человек, измерительная аппаратура и т.п.). Эти нормы выражают через амплитуды боковых составляющих, начиная с которых, можно ограничивать спектр. Таким образом, под шириной спектра ЧМ