Файл: Методические указания и контрольные задания для студентов заочной формы обучения для специальности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 315
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 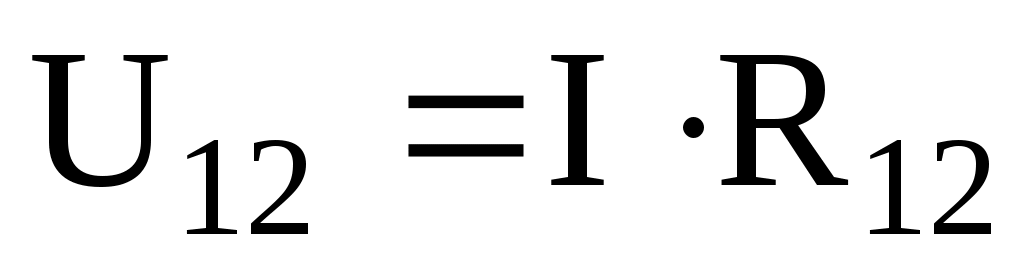 .
.
Выполняем решение, не забывая нумеровать и кратко описывать действия. Именно так решены все типовые примеры пособия.
Выполняем проверку решения следующими способами: проверка результатов с применением первого и второго закона Кирхгофа; подсчетом баланса мощности; сравнение результатов решением задачи другими способами.
Объясним некоторые способы проверки результатов решения.
Применение первого закона Кирхгофа. Формулировка закона: алгебраическая сумма токов в узловой точке равна нулю. Математическая запись для узла б схемы цепи рис.2: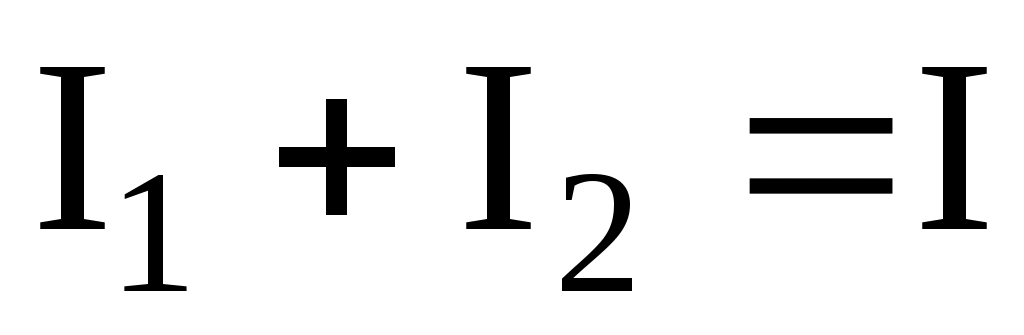 или
или 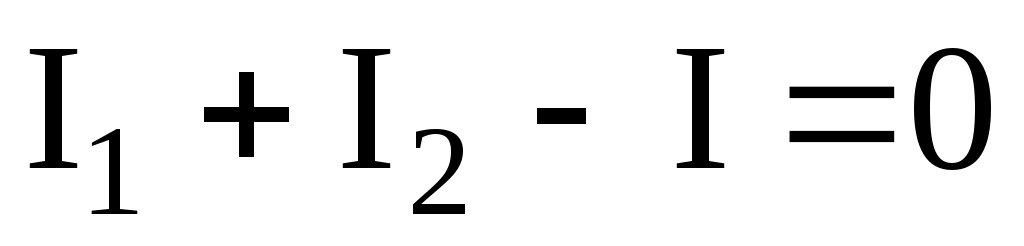 .
.
Применение второго закона Кирхгофа. Формулировка закона: во всяком замкнутом контуре электрической цепи алгебраическая сумма ЭДС ∑Е равна алгебраической сумме падений напряжений ∑IR на отдельных сопротивлениях этого контура.
В замкнутом контуре рис.2 приложенное напряжение U (аналогично ЭДС при внутреннем сопротивлении источника тока, равном нулю) и падения напряжения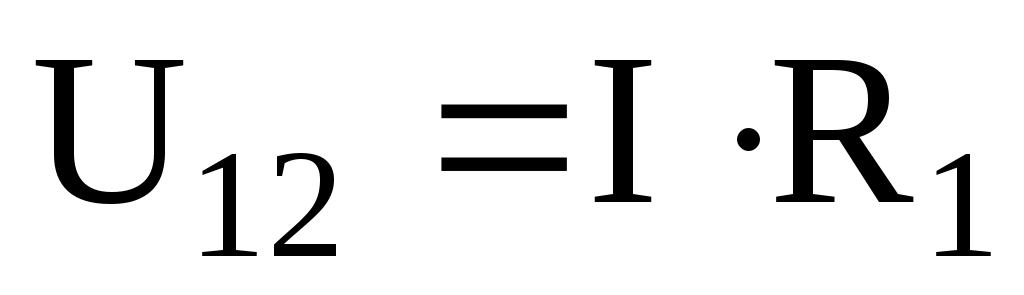 ;
; 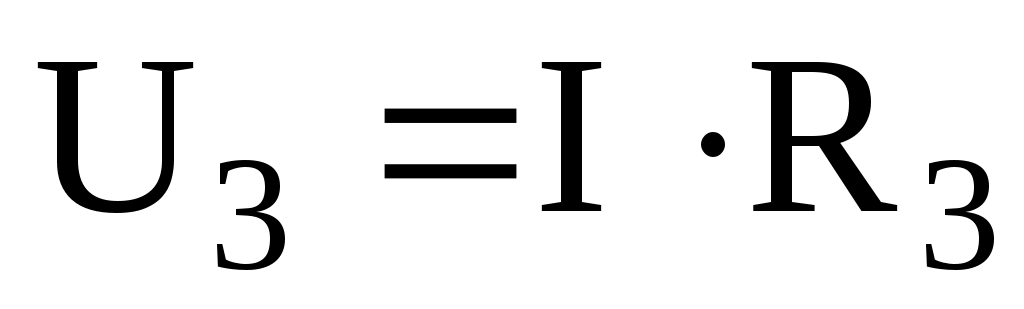 и
и 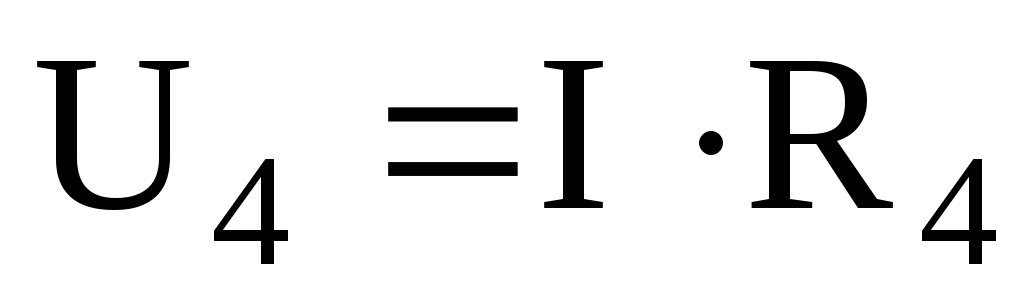 . Обходя контур по направлению тока (в данном случае по часовой стрелке), составим уравнение по второму закону Кирхгофа:
. Обходя контур по направлению тока (в данном случае по часовой стрелке), составим уравнение по второму закону Кирхгофа: 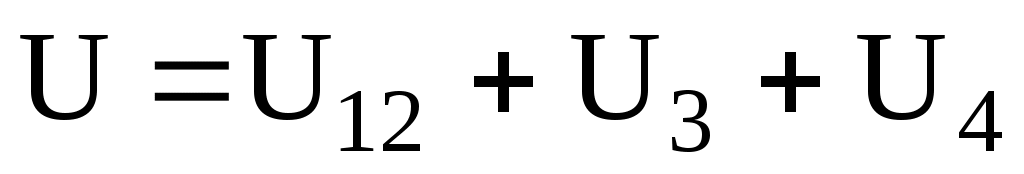 .
.
Подсчет баланса мощности. Общая мощность цепи равна сумме мощностей на отдельных резисторах. Для схемы цепи рис.2
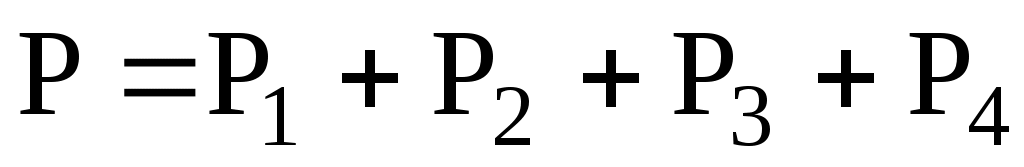 ; т.к.
; т.к. 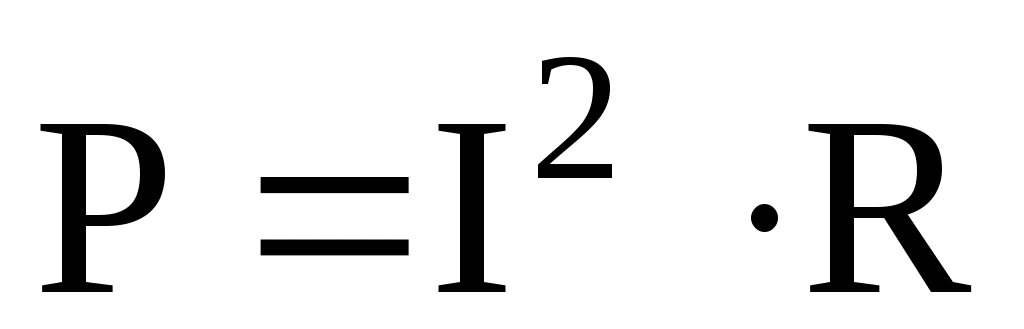 или
или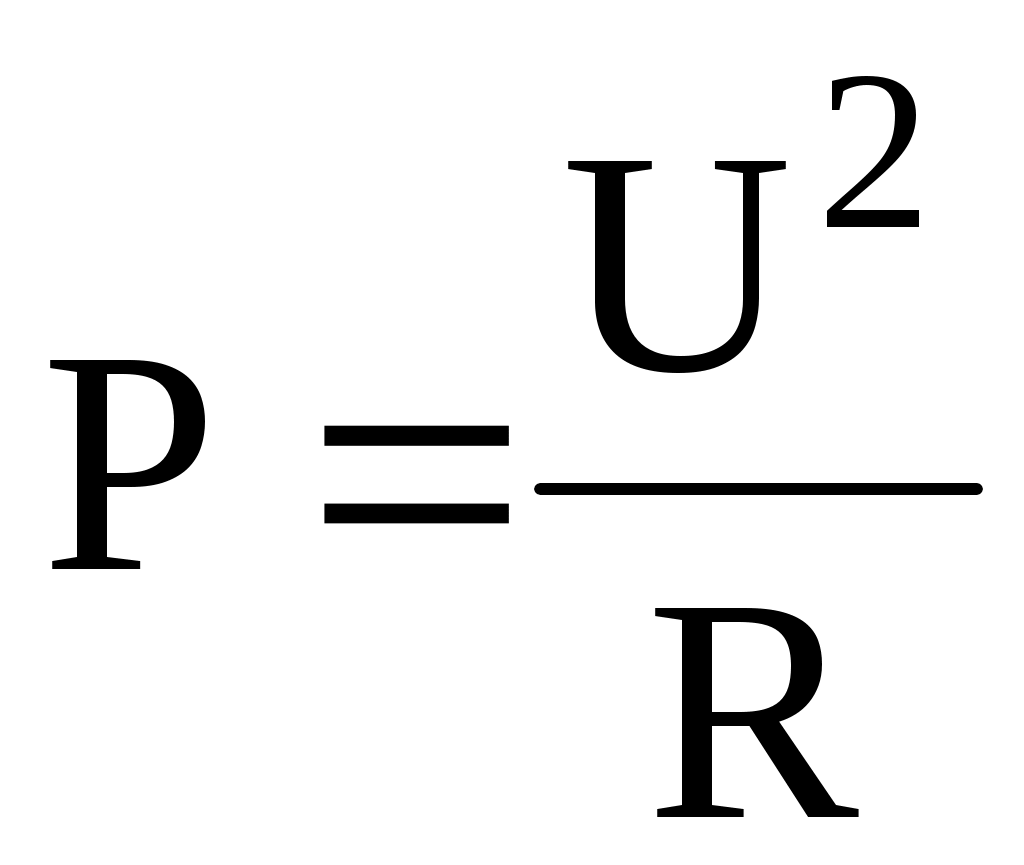 , то
, то 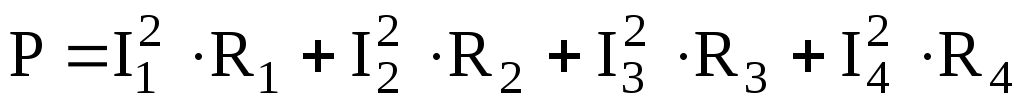 или
или 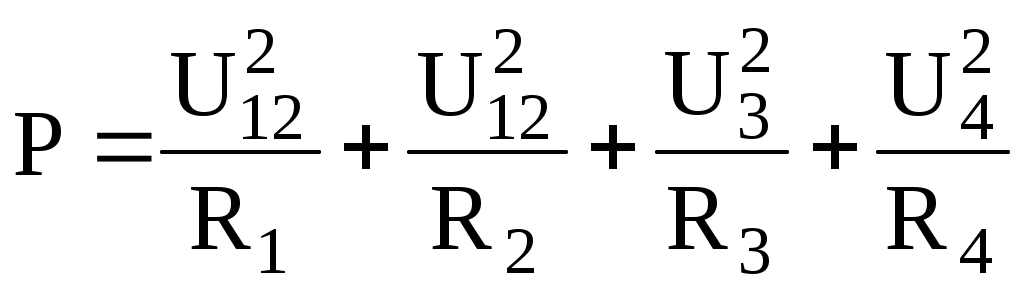 .
.
Если проверку решения проводить путем сравнения результатов решения другими способами, то в данном случае вместо определения тока из формулы
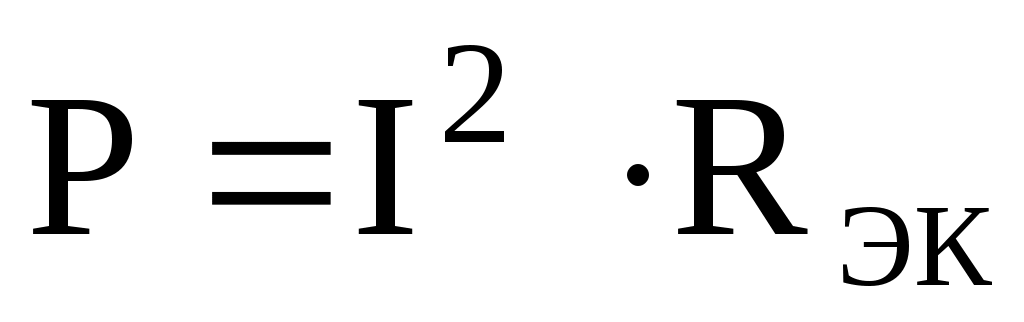 можно было найти напряжение
можно было найти напряжение 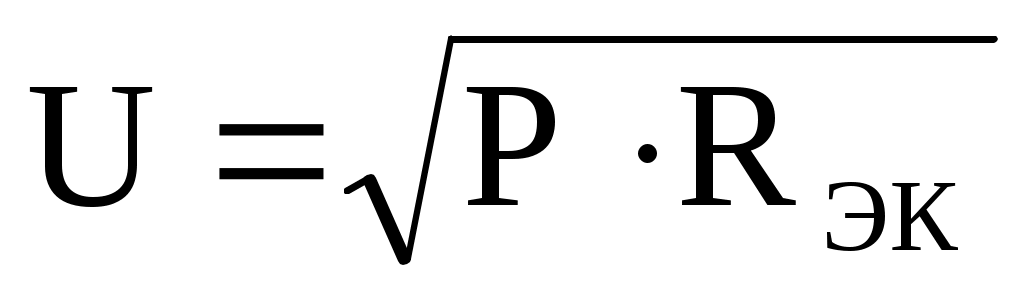 из
из 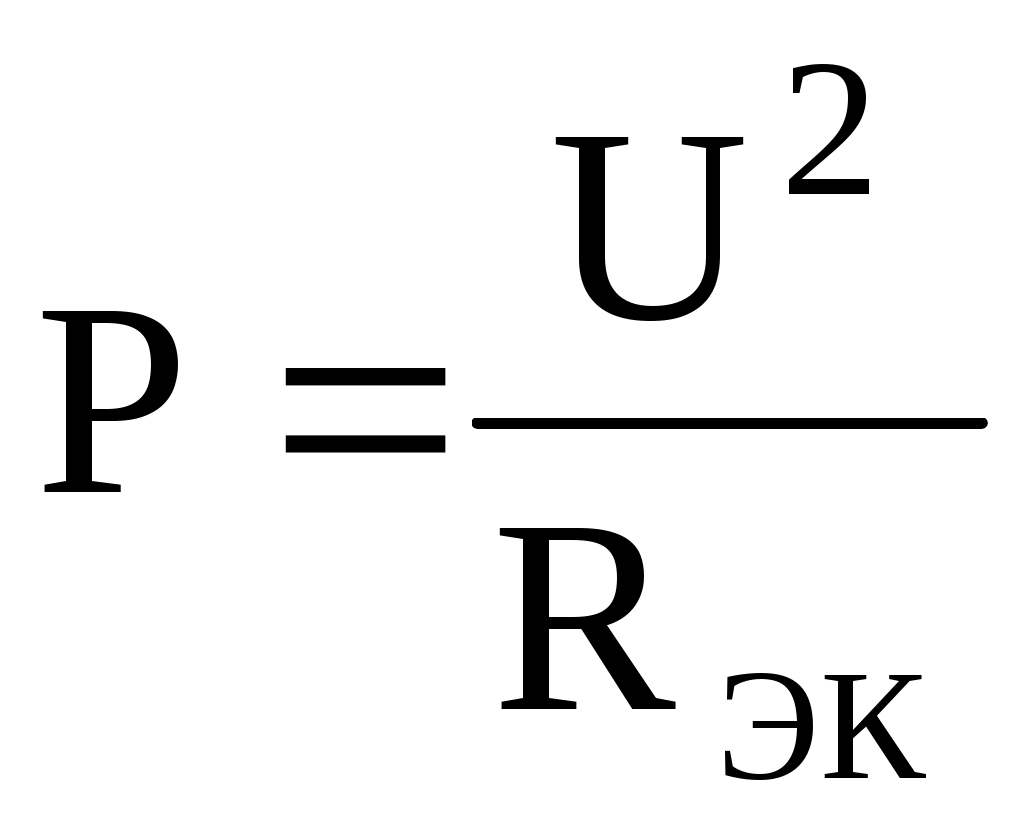 , а затем найти силу тока
, а затем найти силу тока 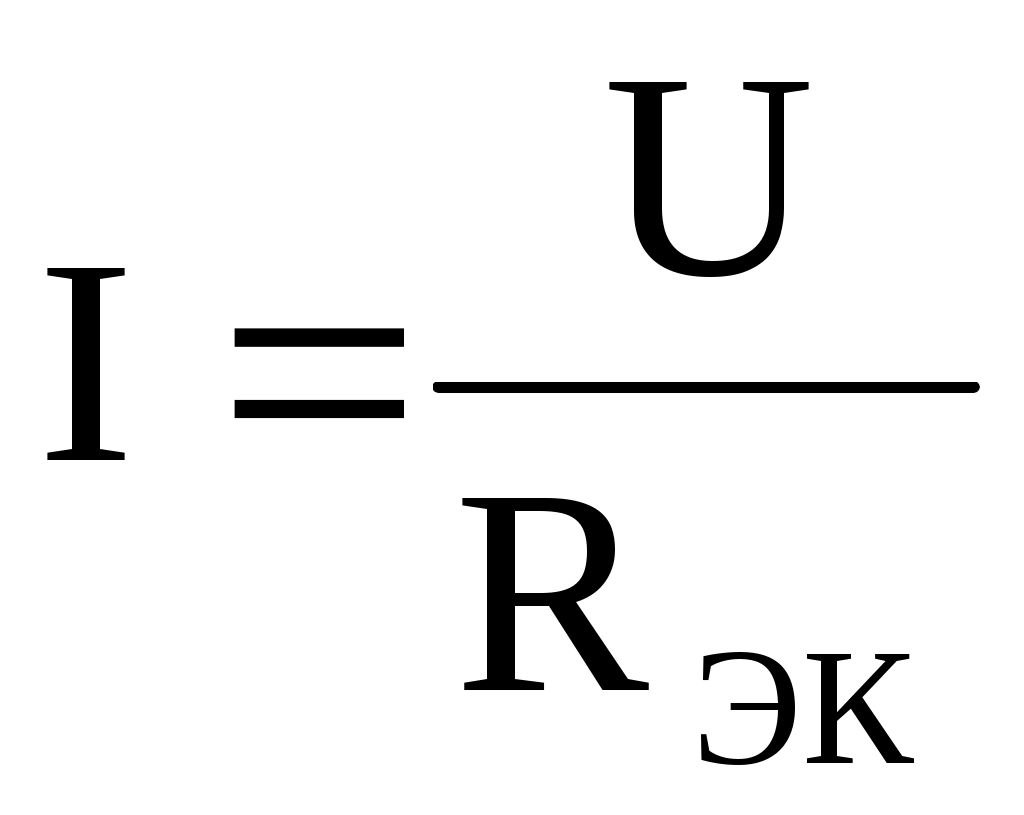 по формуле закона Ома.
по формуле закона Ома.
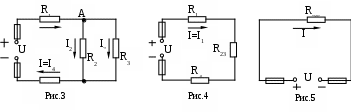
Пример 1. На рис.3 изображена электрическая цепь со смешанным соединением резисторов. Известны значения сопротивлений резисторов R1=3 Ом; R2=10 Ом; R3=15 Ом; R4=1 Ом, напряжение U=110 В и время работы цепи t=10 ч. Определить токи, проходящие через каждый резистор, I1, I2, I3, I4, общую мощность Р и расход энергии W.
Дано: R1=3 Ом; R2=10 Ом; R3=15 Ом; R4=1 Ом; U=110 В; t=10 ч.
Определить: I1, I2, I3, I4, P, W.
Решение:
Обозначим стрелками токи, проходящие через каждый резистор с учетом их направления (рис.3).
Определим общее эквивалентное сопротивление цепи, метод подсчета которого для цепи со смешанным соединением резисторов сводится к последовательному упрощению схемы (рис.4 и рис.5).
Сопротивление R2 и R3 соединены параллельно. Найдем общее сопротивление при таком соединении: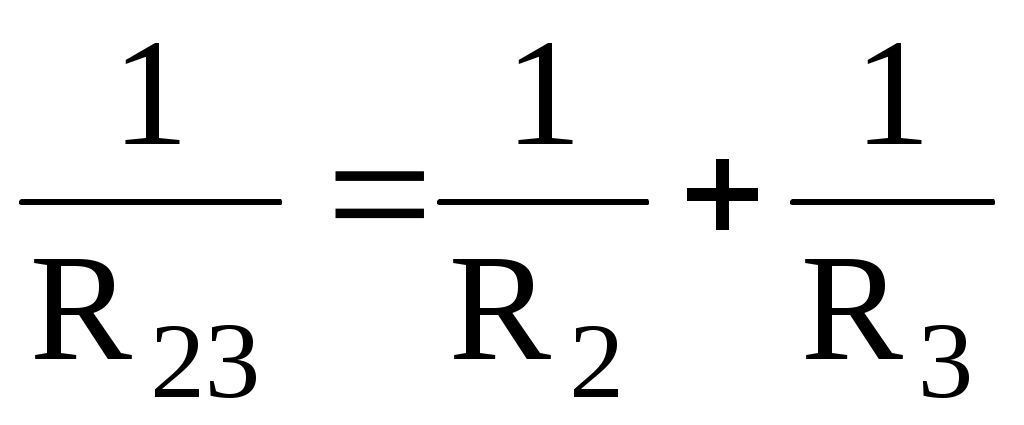 , приводя к общему знаменателю, получим:
, приводя к общему знаменателю, получим:
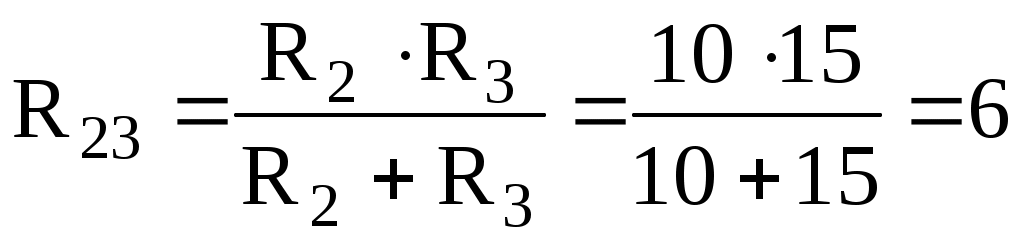 Ом.
Ом.
Схема примет вид, указанный на рис.4.
Теперь резисторы R23, R1, R4 соединены последовательно, их общее сопротивление:
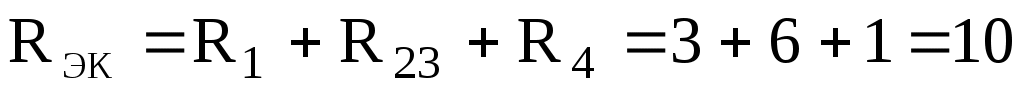 Ом.
Ом.
Это общее сопротивление, включенное в цепь вместо четырех сопротивлений схемы рис.3, при таком же значении напряжения не изменит тока в цепи. Поэтому это сопротивление чаще называется общим эквивалентным сопротивлением цепи или просто эквивалентным (рис.5).
По закону Ома для внешнего участка цепи определим ток:
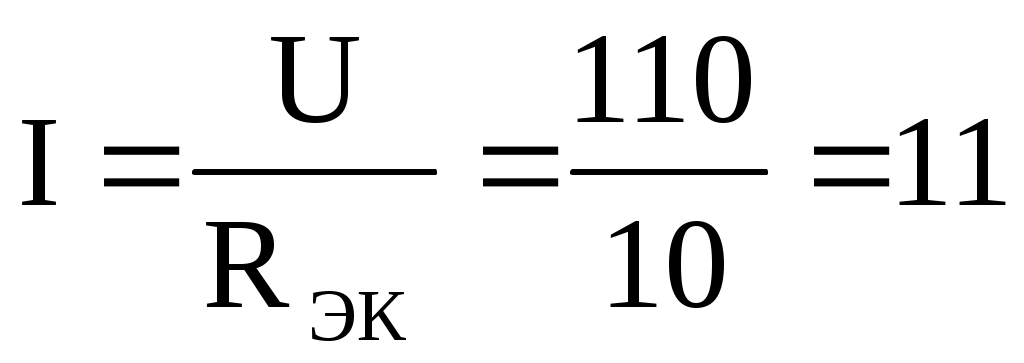 А.
А.
Найдем токи, проходящие через все резисторы. Через резистор R1 проходит ток I1=I. Через резистор R4 проходит ток I4=I.
Для определения токов, проходящих через резисторы R2 и R3, нужно найти напряжение на параллельном участке U
23. Это напряжение можно определить двумя способами:
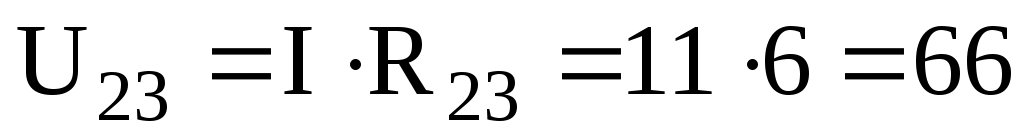 В,
В,
или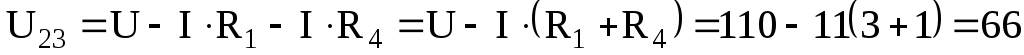 В.
В.
По закону Ома для параллельного участка цепи найдем:
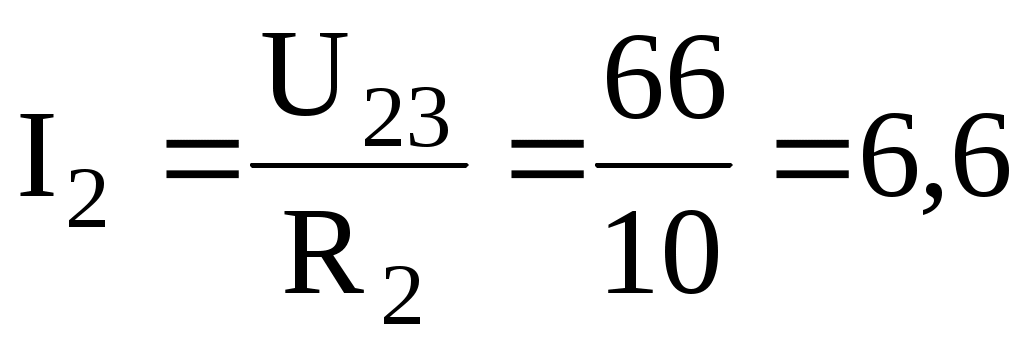 А;
А; 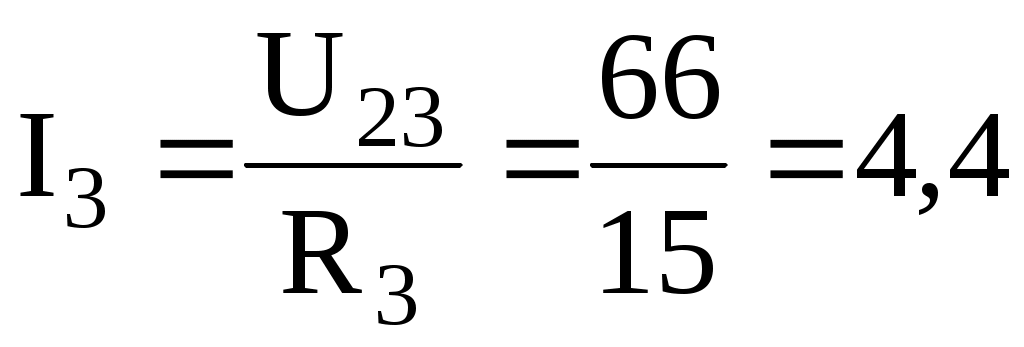 А
А
или, применяя первый закон Кирхгофа, получим:
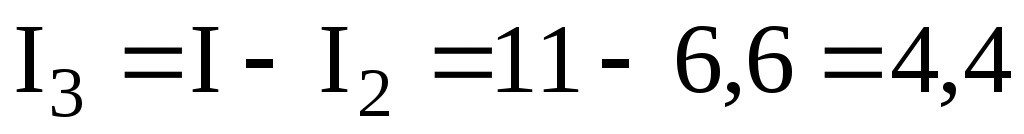 А.
А.
Найдем общую мощность цепи:
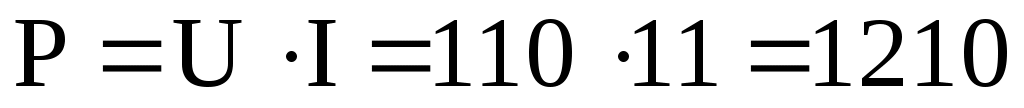 Вт=1,21 кВт.
Вт=1,21 кВт.
Определим расход энергии:
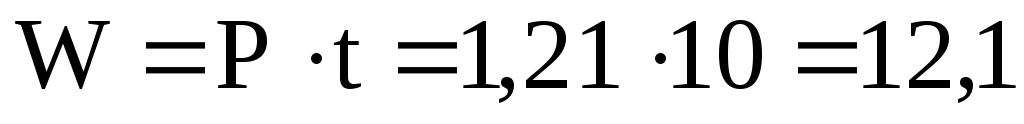 кВт∙ч.
кВт∙ч.
Выполним проверку решения задачи описанными ранее способами:
а) проверим баланс мощности:
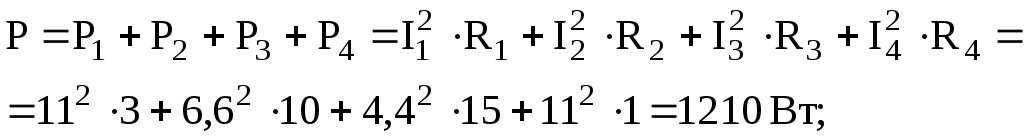
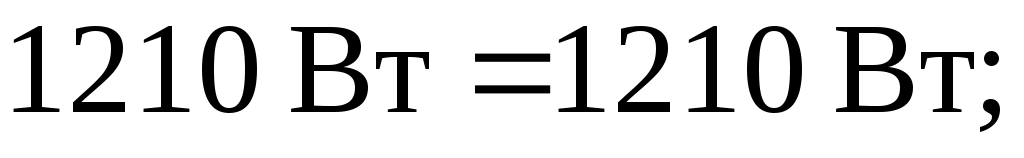
б) для узловой точки А схемы рис.3 применим первый закон Кирхгофа:
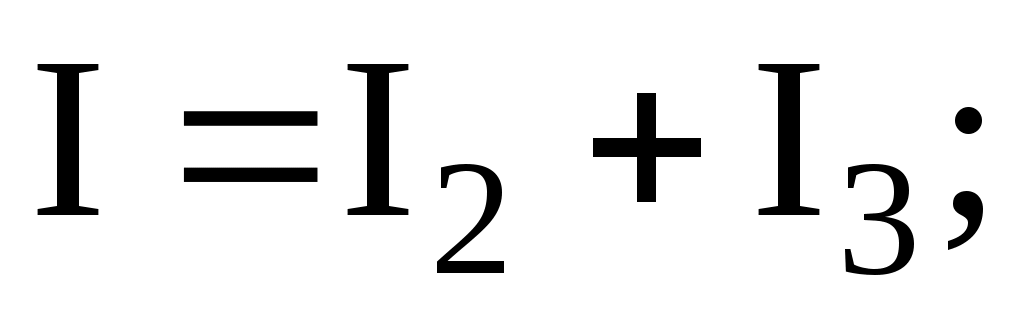
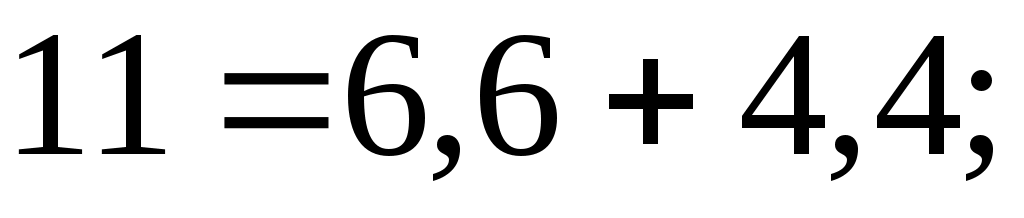
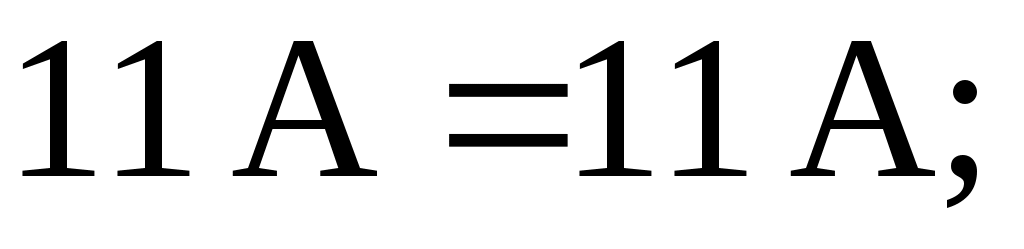
в) составим уравнение по второму закону Кирхгофа, обходя контур цепи по часовой стрелке:
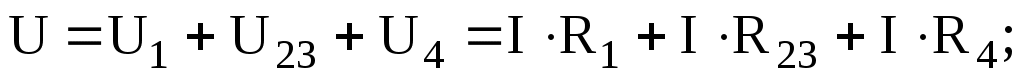
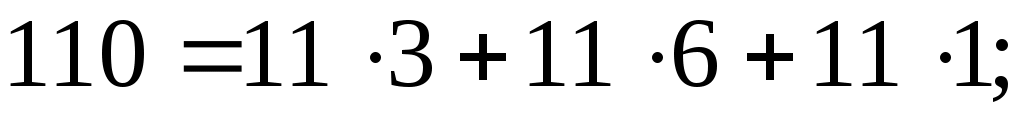
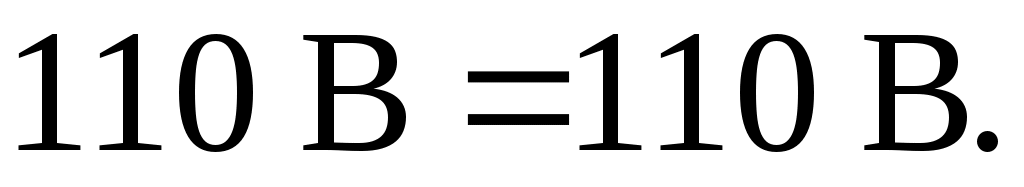
Все способы проверки подтверждают правильность решения задачи. В вашем варианте достаточно применить только тот способ, который предусмотрен условием.
Пример 2. Электрическая цепь, состоящая из нескольких резисторов, имеет эквивалентное сопротивление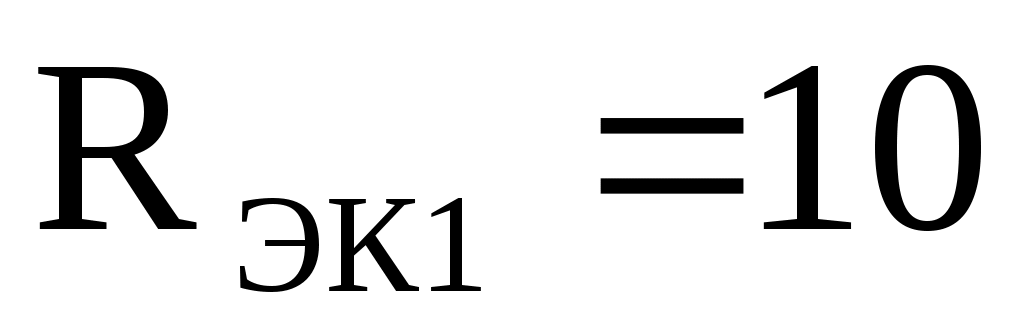 Ом. Каким способом и какой по значению сопротивления резистор
Ом. Каким способом и какой по значению сопротивления резистор 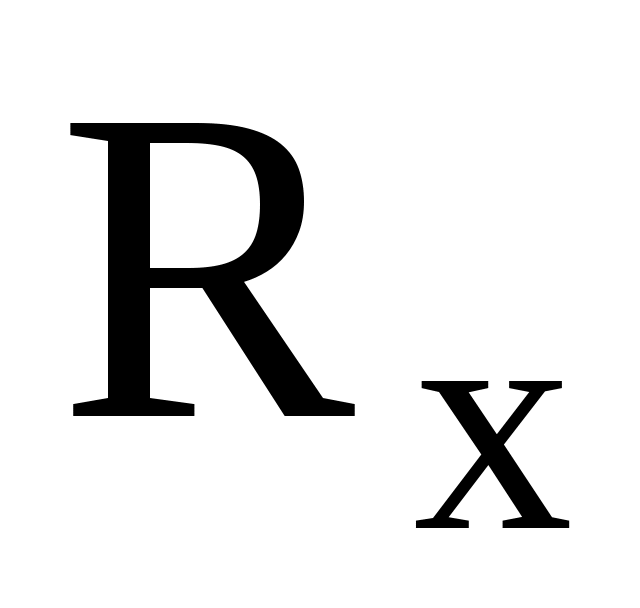
следует подключить к цепи, чтобы увеличить эквивалентное сопротивление этой цепи до величины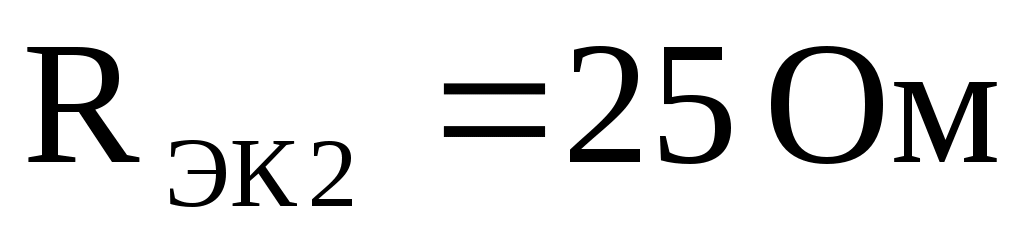 ?
?
Дано: Ом,
Ом, 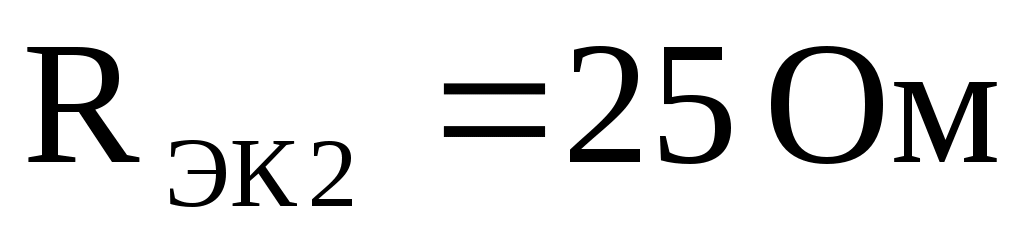 . Определить значение и способ подключения
. Определить значение и способ подключения  .
.
Решение: При последовательном соединении резисторов эквивалентное сопротивление цепи равно сумме их сопротивлений. Так как эквивалентное сопротивление цепи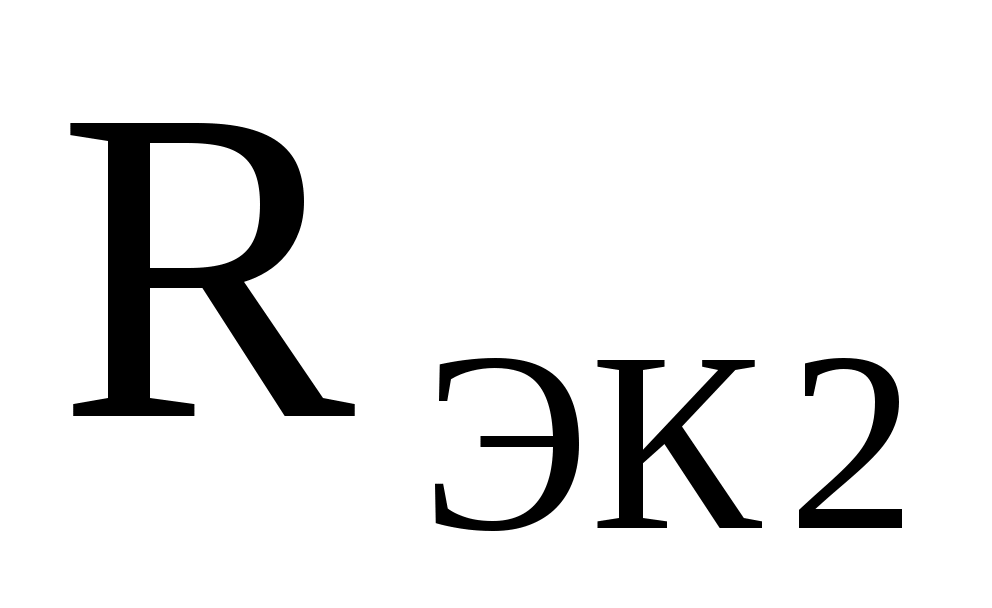 по сравнению с прежним значением
по сравнению с прежним значением 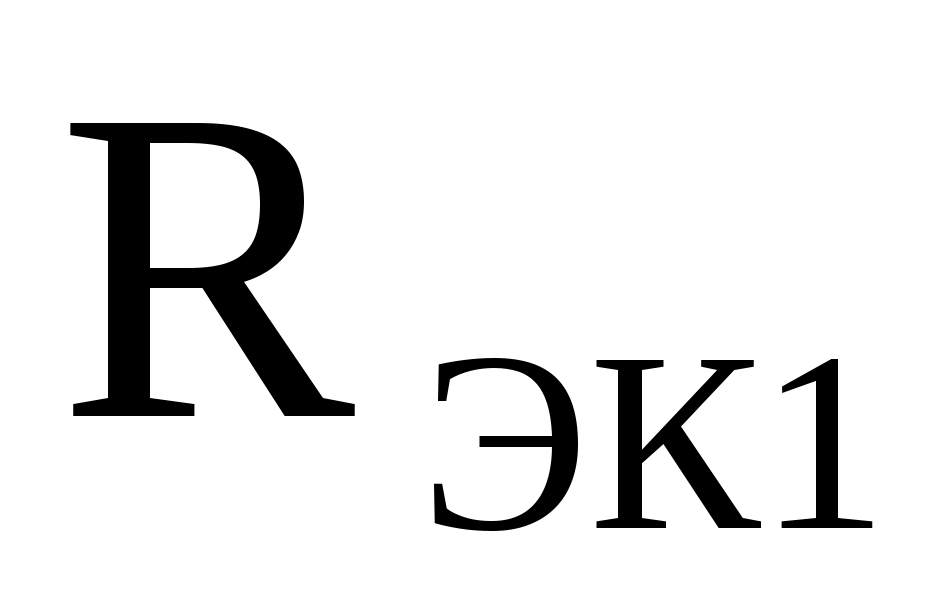 увеличивается, то резистор
увеличивается, то резистор  надо включить в цепь последовательно:
надо включить в цепь последовательно:
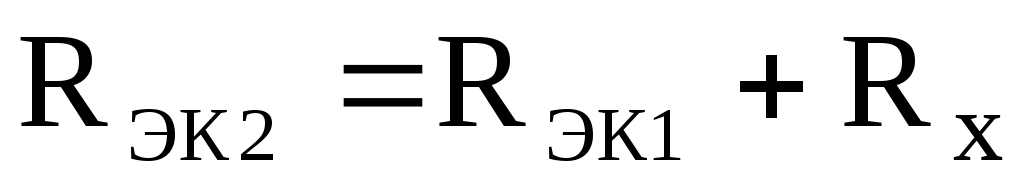 ,
, 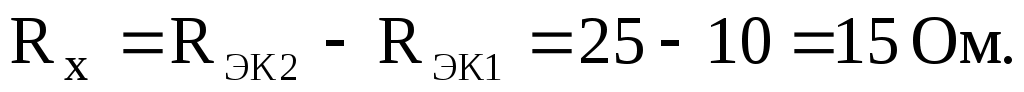
Ответ: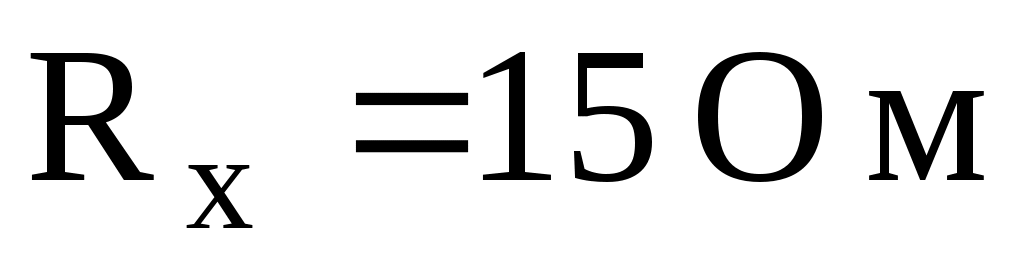 (рис.6).
(рис.6).
Пример 3. Электрическая цепь, состоящая из нескольких резисторов, имеет эквивалентное сопротивление Ом. Каким способом и какое по значению сопротивление резистора
Ом. Каким способом и какое по значению сопротивление резистора  следует подключить, чтобы уменьшить эквивалентное сопротивление цепи до
следует подключить, чтобы уменьшить эквивалентное сопротивление цепи до 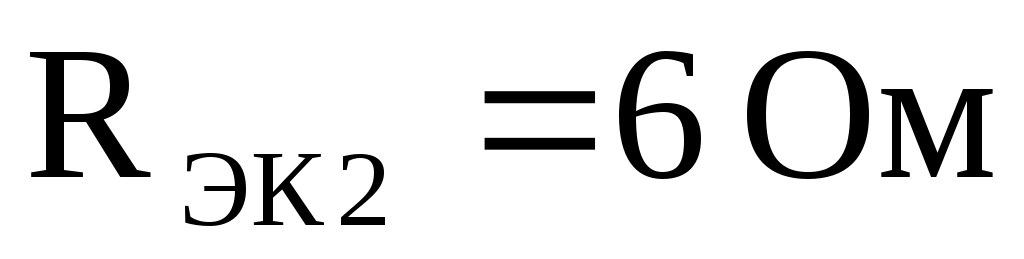 ?
?
Дано: Ом,
Ом, 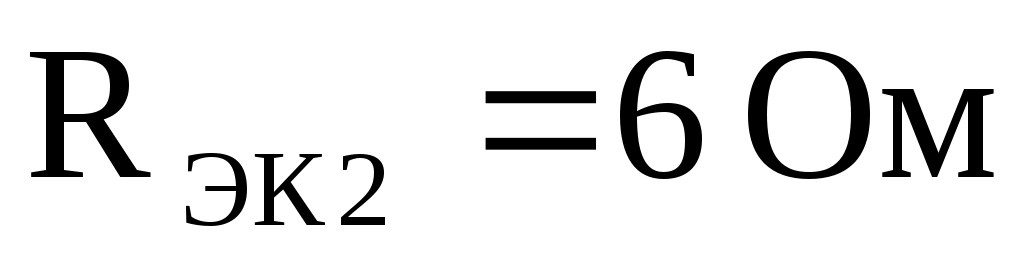 . Определить значение и способ подключения
. Определить значение и способ подключения  .
.
Решение. При параллельном соединении резисторов обратное значение эквивалентного сопротивления цепи равно сумме обратных значений сопротивлений отдельных резисторов:
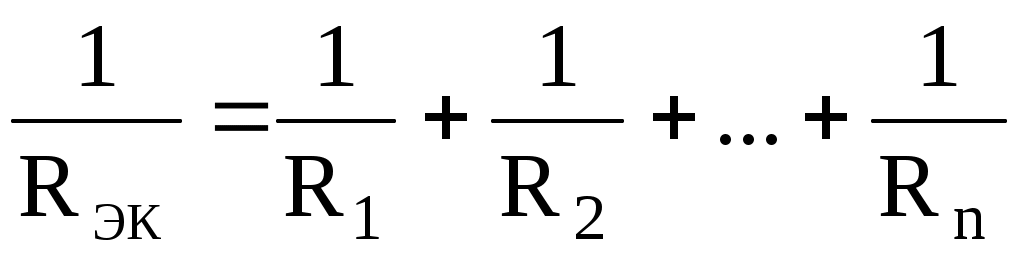
и будет меньше наименьшего сопротивления резисторов. Например, параллельно соединены резисторы сопротивлениями 100, 50, 10, 0,5 Ом. Эквивалентное сопротивление такого соединения меньше 0,5 Ом.
По условию задачи, эквивалентное сопротивление меньше первоначального значения
меньше первоначального значения  , поэтому резистор
, поэтому резистор 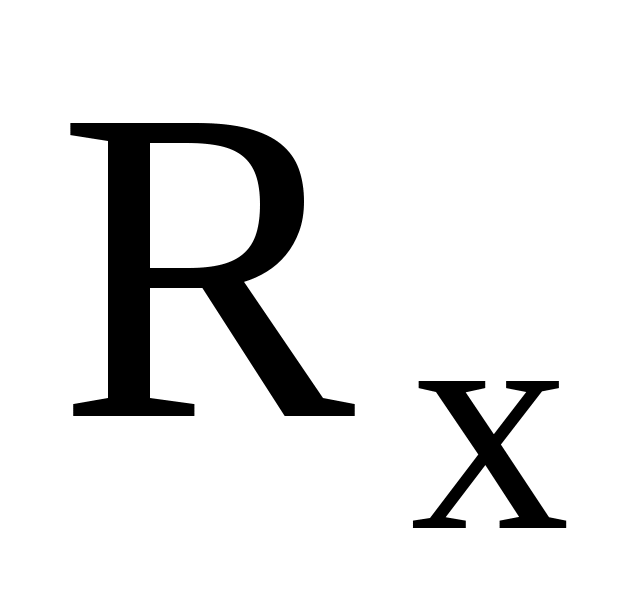 подключается к цепи параллельно, а значение его сопротивления определяют следующим образом:
подключается к цепи параллельно, а значение его сопротивления определяют следующим образом:
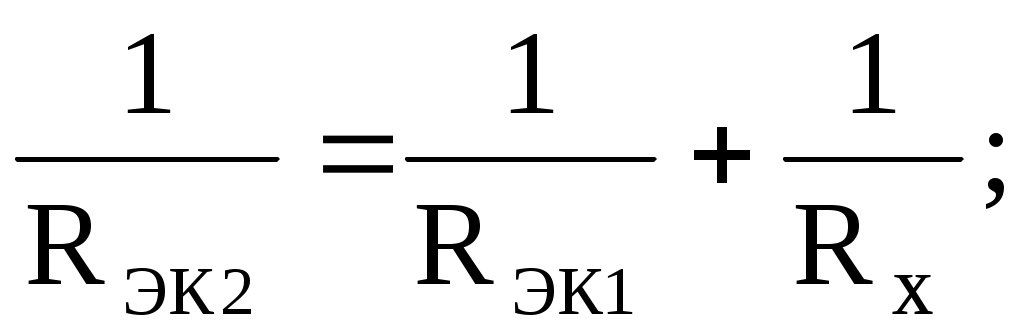

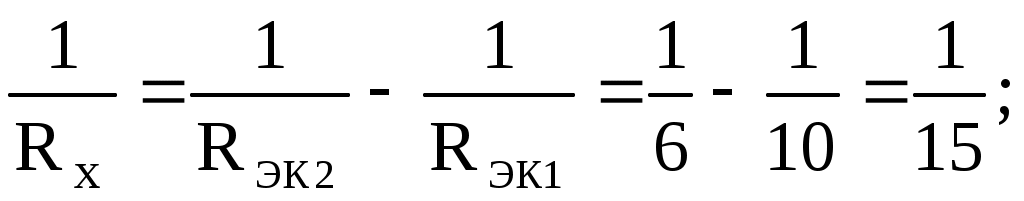
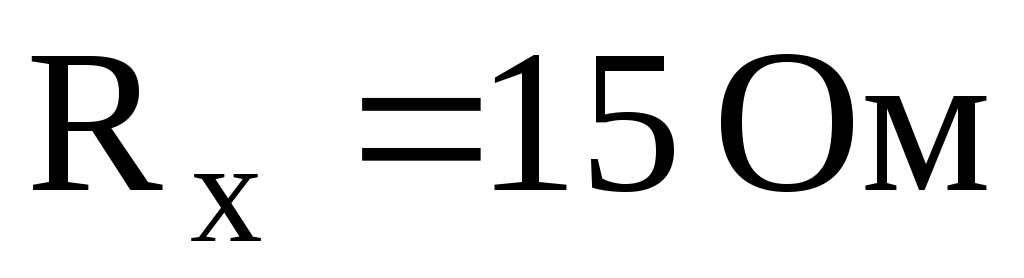 .
.
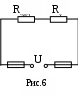
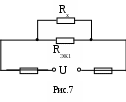
Ответ: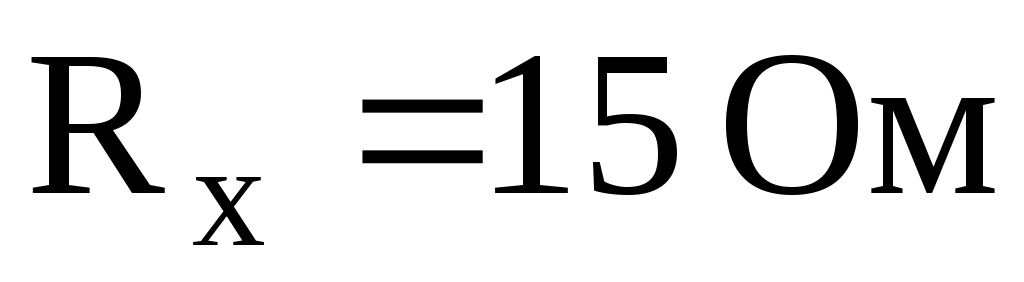 (рис.7).
(рис.7).
Указания к решению задачи 2
Решение задачи 2 требует знания первого и второго законов Кирхгофа.
В любой электрической цепи в соответствии с первым законом Кирхгофа алгебраическая сумма токов, направленных к узлу разветвления, равна нулю:
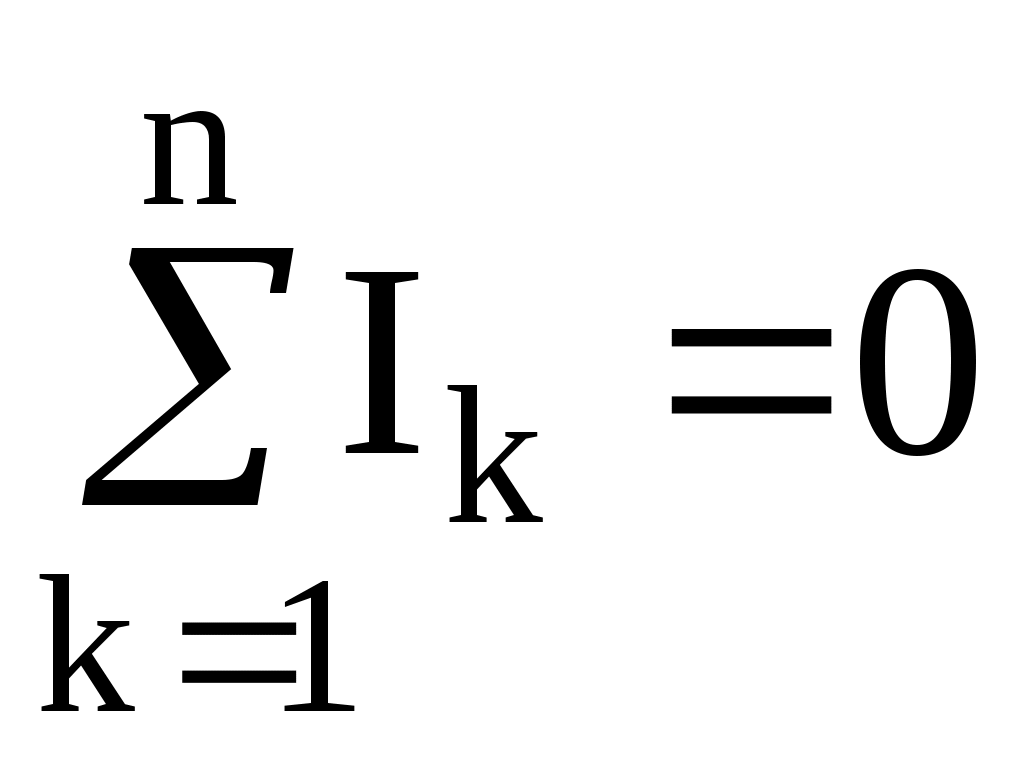 ,
,
где Ik - ток в k–й ветви.
В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС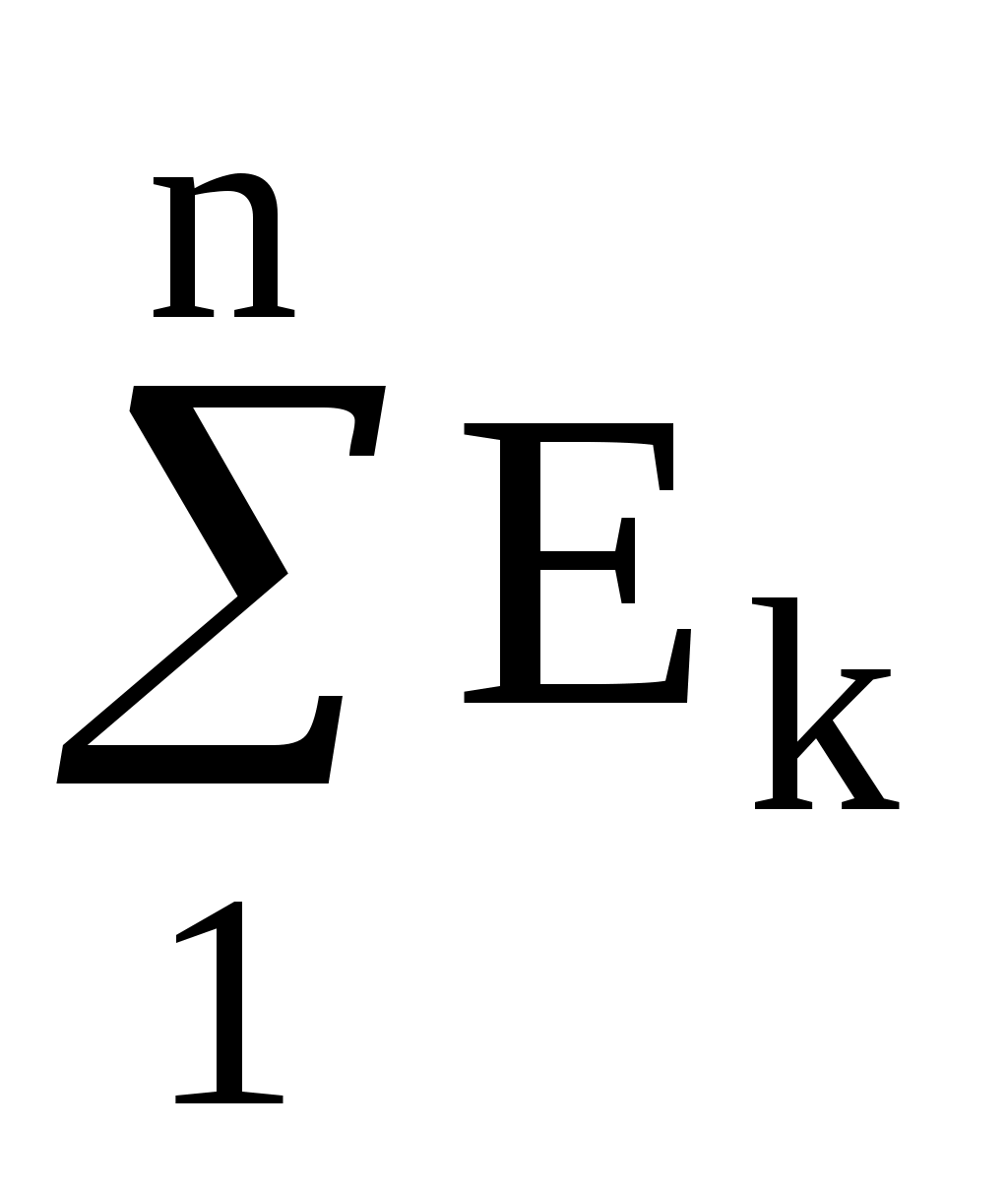 в любом замкнутом контуре электрической цепи равна алгебраической сумме напряжений
в любом замкнутом контуре электрической цепи равна алгебраической сумме напряжений 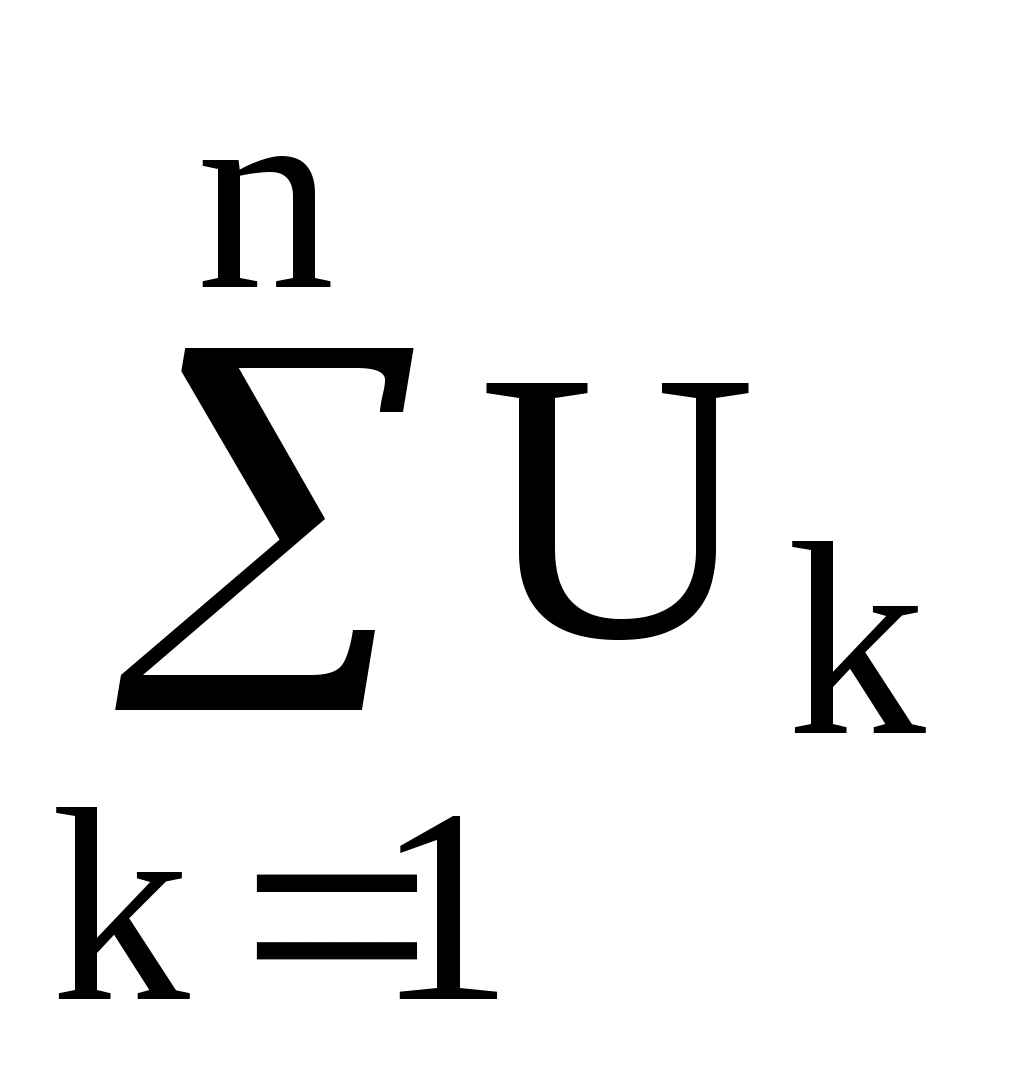 и алгебраической сумме падений напряжения
и алгебраической сумме падений напряжения 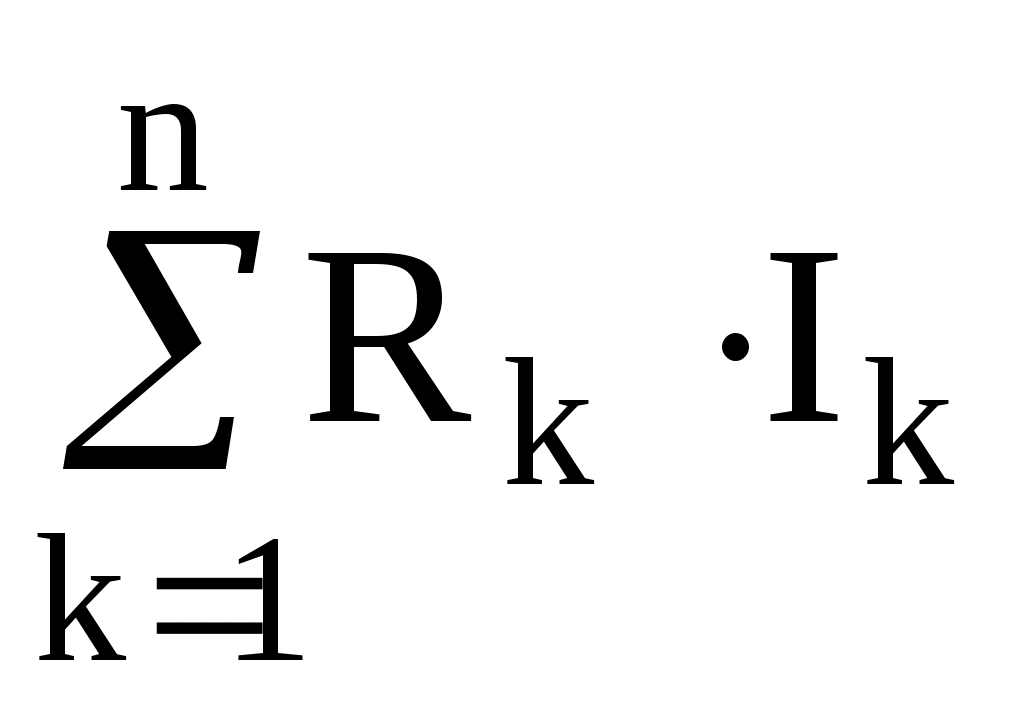 в этом контуре:
в этом контуре:
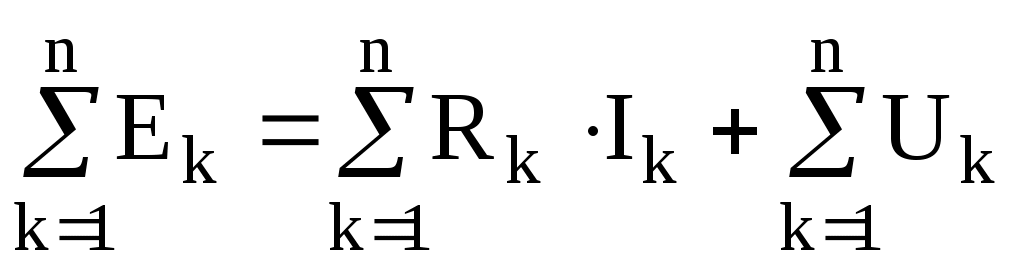 ,
,
где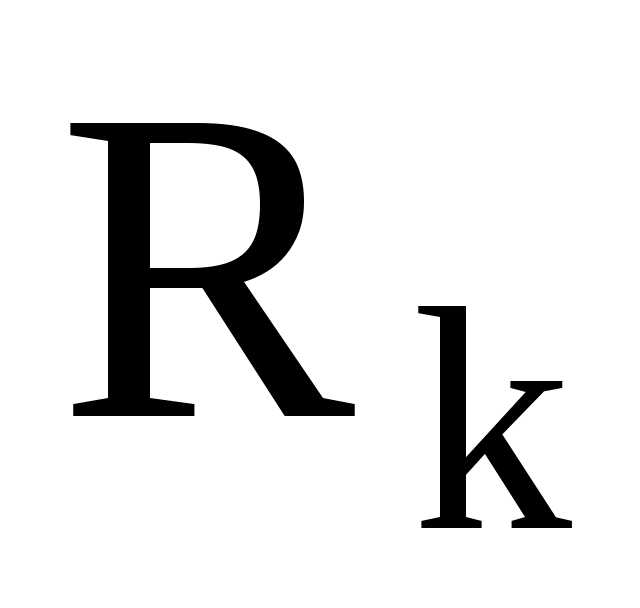 - сопротивление участка цепи рассматриваемого контура;
- сопротивление участка цепи рассматриваемого контура; 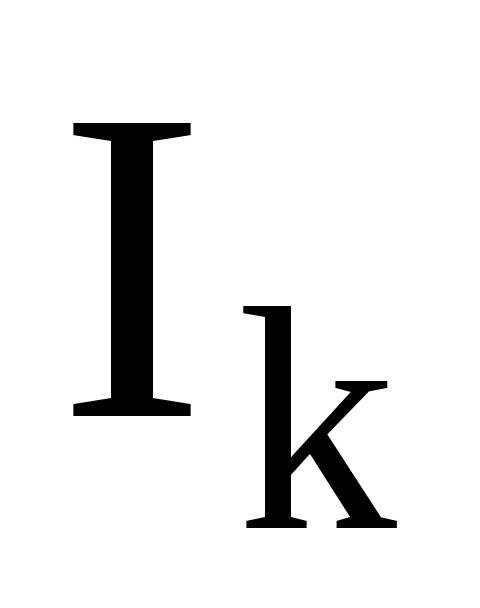 - ток в цепи сопротивления
- ток в цепи сопротивления 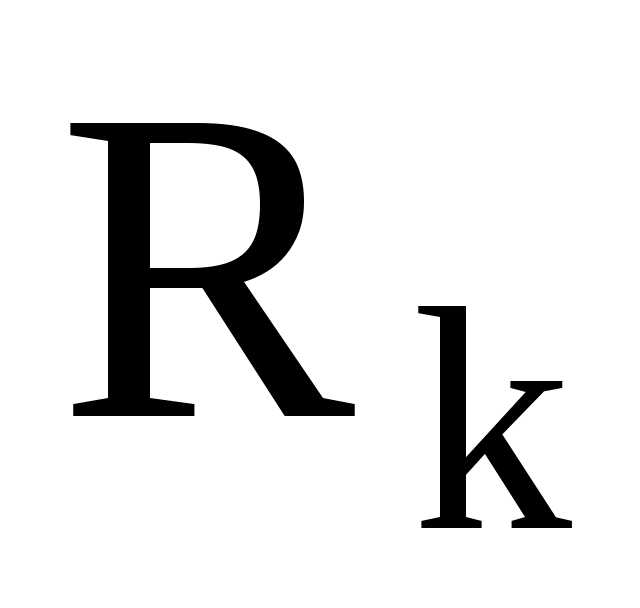
Выполняем решение, не забывая нумеровать и кратко описывать действия. Именно так решены все типовые примеры пособия.
Выполняем проверку решения следующими способами: проверка результатов с применением первого и второго закона Кирхгофа; подсчетом баланса мощности; сравнение результатов решением задачи другими способами.
Объясним некоторые способы проверки результатов решения.
Применение первого закона Кирхгофа. Формулировка закона: алгебраическая сумма токов в узловой точке равна нулю. Математическая запись для узла б схемы цепи рис.2:
Применение второго закона Кирхгофа. Формулировка закона: во всяком замкнутом контуре электрической цепи алгебраическая сумма ЭДС ∑Е равна алгебраической сумме падений напряжений ∑IR на отдельных сопротивлениях этого контура.
В замкнутом контуре рис.2 приложенное напряжение U (аналогично ЭДС при внутреннем сопротивлении источника тока, равном нулю) и падения напряжения
Подсчет баланса мощности. Общая мощность цепи равна сумме мощностей на отдельных резисторах. Для схемы цепи рис.2
Если проверку решения проводить путем сравнения результатов решения другими способами, то в данном случае вместо определения тока из формулы
Пример 1. На рис.3 изображена электрическая цепь со смешанным соединением резисторов. Известны значения сопротивлений резисторов R1=3 Ом; R2=10 Ом; R3=15 Ом; R4=1 Ом, напряжение U=110 В и время работы цепи t=10 ч. Определить токи, проходящие через каждый резистор, I1, I2, I3, I4, общую мощность Р и расход энергии W.

Дано: R1=3 Ом; R2=10 Ом; R3=15 Ом; R4=1 Ом; U=110 В; t=10 ч.
Определить: I1, I2, I3, I4, P, W.
Решение:
Обозначим стрелками токи, проходящие через каждый резистор с учетом их направления (рис.3).
Определим общее эквивалентное сопротивление цепи, метод подсчета которого для цепи со смешанным соединением резисторов сводится к последовательному упрощению схемы (рис.4 и рис.5).
Сопротивление R2 и R3 соединены параллельно. Найдем общее сопротивление при таком соединении:
Схема примет вид, указанный на рис.4.
Теперь резисторы R23, R1, R4 соединены последовательно, их общее сопротивление:
Это общее сопротивление, включенное в цепь вместо четырех сопротивлений схемы рис.3, при таком же значении напряжения не изменит тока в цепи. Поэтому это сопротивление чаще называется общим эквивалентным сопротивлением цепи или просто эквивалентным (рис.5).
По закону Ома для внешнего участка цепи определим ток:
Найдем токи, проходящие через все резисторы. Через резистор R1 проходит ток I1=I. Через резистор R4 проходит ток I4=I.
Для определения токов, проходящих через резисторы R2 и R3, нужно найти напряжение на параллельном участке U
23. Это напряжение можно определить двумя способами:
или
По закону Ома для параллельного участка цепи найдем:
или, применяя первый закон Кирхгофа, получим:
Найдем общую мощность цепи:
Определим расход энергии:
Выполним проверку решения задачи описанными ранее способами:
а) проверим баланс мощности:
б) для узловой точки А схемы рис.3 применим первый закон Кирхгофа:
в) составим уравнение по второму закону Кирхгофа, обходя контур цепи по часовой стрелке:
Все способы проверки подтверждают правильность решения задачи. В вашем варианте достаточно применить только тот способ, который предусмотрен условием.
Пример 2. Электрическая цепь, состоящая из нескольких резисторов, имеет эквивалентное сопротивление
следует подключить к цепи, чтобы увеличить эквивалентное сопротивление этой цепи до величины
Дано:
Решение: При последовательном соединении резисторов эквивалентное сопротивление цепи равно сумме их сопротивлений. Так как эквивалентное сопротивление цепи
Ответ:


Пример 3. Электрическая цепь, состоящая из нескольких резисторов, имеет эквивалентное сопротивление
Дано:
Решение. При параллельном соединении резисторов обратное значение эквивалентного сопротивления цепи равно сумме обратных значений сопротивлений отдельных резисторов:
и будет меньше наименьшего сопротивления резисторов. Например, параллельно соединены резисторы сопротивлениями 100, 50, 10, 0,5 Ом. Эквивалентное сопротивление такого соединения меньше 0,5 Ом.
По условию задачи, эквивалентное сопротивление
Ответ:
Указания к решению задачи 2
Решение задачи 2 требует знания первого и второго законов Кирхгофа.
В любой электрической цепи в соответствии с первым законом Кирхгофа алгебраическая сумма токов, направленных к узлу разветвления, равна нулю:
где Ik - ток в k–й ветви.
В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС
где