Файл: Методические указания и контрольные задания для студентов заочной формы обучения для специальности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 316
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Примечание. Следует обратить внимание на последовательность записи решения задач: вначале пишем формулу, затем подставляем числовые значения электрических величин и после этого выполняем арифметические действия и пишем ответ, с указанием размерности определяемой величины. При такой записи удобно проверить все действия, старайтесь ее соблюдать!
Пример 7. Определить ток, полную, активную и реактивную мощности, а также напряжения на отдельных участках цепи, изображенной на рис.10, если
Дано:
Определить: I, S, P, Q,
Решение: Индуктивное сопротивление цепи:
Емкостное сопротивление цепи:
Полное сопротивление цепи:
Ток в цепи:
Коэффициент мощности цепи:
;
Полная, активная и реактивная мощности:
Напряжения на отдельных участках цепи:
Ответ:
Пример 8. Неразветвленная цепь переменного тока содержит катушку с активным сопротивлением
Дано:
Ом;
Определить:
Решение: Определим полное сопротивление цепи:
Определим ток цепи:
Найдем коэффициент мощности цепи. Во избежание потери знака угла (косинус – функция четная) определим
По таблице Брадиса определим коэффициент мощности:
Определим активную, реактивную и полную мощности цепи:
Найдем падение напряжения на сопротивлениях цепи:
;
Построение векторной диаграммы начнем с выбора масштаба для тока и напряжения. Задаемся масштабом по току:
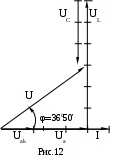
Из конца вектора
Из конца вектора
Геометрическая сумма векторов
равна полному напряжению
Характер нагрузки активно – индуктивный, напряжение опережает ток на угол