Файл: Механика. Электричество. Магнетизм.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 148

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ ПРИ ПОМОЩИ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Определение момента инерции маятника обербека

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ Цели работы: экспериментально исследовать квазистационарное электрическое поле, построить картину эквипотенциальных поверхностей и линий напряженности этого поля; определить значение модуля напряженности электрического поля в указанных точках. Приборы и принадлежности: электролитическая ванна; источник переменного напряжения; потенциометр с зондом. Подготовка к работеПо лекциям и приведенному ниже списку литературы изучите следующие вопросы: закон Кулона; понятие электрического поля; напряженность электрического поля, линии напряженности; потенциал электрического поля, эквипотенциальные линии; связь между напряженностью поля и потенциалом. Вопросы для допуска к работе Что называется напряженностью электрического поля? Что такое силовая линия электрического поля? Что называется потенциалом электростатического поля? Как расположены друг относительно друга в пространстве линии напряженности и эквипотенциальные поверхности? Как связаны между собой напряженность и потенциал в данной точке? Каковы условия равновесия зарядов на проводнике в электростатическом поле? Теоретическое введениеЭлектрическое поле возникает в пространстве при наличии заряженных тел. Неподвижные заряды создают поле, которое называется электростатическим. В природе существуют электрические заряды двух знаков: положительные «+» и отрицательные «–», это наименование условно. Наименьшим зарядом обладают элементарные частицы, например: электрон – частица, входящая в состав атома, – имеет отрицательный заряд –е (здесь е = 1,6 ∙ 10-19 Кл – «элементарный заряд»), а протоны входящие в состав ядра атома, заряжены положительно (+е). Заряды одинакового знака отталкиваются друг от друга, заряды противоположных знаков – притягиваются.По закону Кулона, силы взаимодействия двух точечных неподвижных зарядов q1 и q2 направлены вдоль прямой, их соединяющей, прямо пропорциональны величинам зарядов и обратно пропорциональны квадрату расстояния r12 между зарядами: (3.1)где – единичный вектор, направленный от одного заряда к другому, ε0 = 8,85 ∙ 10-12 Ф/м – электрическая постоянная,ε – диэлектрическая проницаемость среды.Эти силы являются центральными и, следовательно, консервативными.Отношение силы, действующей на пробный заряд, к величине этого заряда не зависит от величины заряда и называется напряженностью электрического поля . (3.2)Напряженность – векторная величина, ее направление совпадает с направлением силы , действующей на пробный положительный заряд , находящийся в данной точке пространства.Электростатическое поле можно представить графически с помощью системы линий напряженности (силовых линий), начинающихся на положительных зарядах и заканчивающихся на отрицательных или уходящих на бесконечность. Вектор напряженности в каждой точке силовой линии направлен по касательной к ней и совпадает с ней по направлению. Густота силовых линий пропорциональна модулю вектора напряженности .Сила, действующая на произвольный точечный заряд, помещенный в данную точку поля, определяется произведением величины этого заряда на напряженность электрического поля в данной точке . (3.3)Работа консервативных электростатических сил по перемещению заряда в электростатическом поле не зависит от траектории движения, а определяется лишь начальным и конечным положением заряда, эта работа может быть выражена через изменение потенциальной энергии заряда со знаком «–»: (3.4)Потенциальная энергия точечного заряда в электростатическом поле может быть выражена через энергетическую характеристику этого поля, называемую потенциалом φ, как произведение , следовательно, разность потенциалов между точками 1 и 2 можно определить через отношение работы сил поля к величине заряда (3.5)При бесконечно малом перемещении заряда под действием силы в произвольном направлении совершается элементарная работа . Тогда из (3.5), с учетом (3.3), получим, что для электростатического поля малая разность потенциалов связана с напряженностью выражением (3.6)где – проекция вектора на перемещение .Следовательно, . (3.7)В декартовой системе вектор напряженности электростатического поля может быть выражен через свои проекции Ex, Ey, Ez на оси соответственно: (3.8)где – орты координатных осей.Из математического определения частной производной функции многих переменных, применительно к функции и уравнения (3.7) следует (3.9)Это означает, что напряженность электростатического поля в любой точке может быть выражена через градиент потенциала в этой точке: (3.10)Напомним, что градиентом функции в векторной алгебре называется вектор, проекции которого на координатные оси равны частным производным от данной функции по соответствующим координатам. Градиент функции направлен в сторону ее наиболее быстрого возрастания, поэтому формула (3.10) показывает, что вектор напряженности направлен в сторону максимального убывания потенциала.Поверхности равного потенциала называются эквипотенциальными. Из соотношения (3.6) следует, что при перемещении заряда вдоль эквипотенциальной поверхности (d = 0) работа электростатического поля равна нулю, и это возможно только в том случае, когда вектор напряженности перпендикулярен этой поверхности (cos  = 0). Следовательно, силовые линии электростатического поля пересекают эквипотенциальные поверхности под прямым углом (рис. 3.1). Рис. 3.1. Взаимное расположение в пространстве силовых линий и эквипотенциальных поверхностей:1, 2 – проводники; 3 – эквипотенциальная поверхность;4 – линия напряженностиВнутри проводника всегда имеются свободные заряженные частицы, поэтому при внесении проводника во внешнее электростатическое поле свободные положительные заряды начинают двигаться в направлении вектора , а отрицательные – в противоположную сторону, на поверхности проводника образуются так называемые индуцированные заряды. Поле этих зарядов направлено противоположно внешнему полю. Перераспределение зарядов на проводнике будет происходить до тех пор, пока не будут выполнены следующие условия: (3.11)то есть: а) напряженность электрического поля внутри проводника равна 0; б) на поверхности проводника существует только нормальная составляющая электрического поля . Следовательно, поверхность проводника является эквипотенциальной и линии напряженности внешнего электрического поля перпендикулярны этой поверхности (см. рис. 3.1).Электрическое поле, напряженность которого одинакова во всех точках: называют однородным. Очевидно, что линии напряженности такого поля представляют собой параллельные прямые. Соответственно, эквипотенциальными поверхностями будут перпендикулярные к ним параллельные плоскости. Однородное поле возникает, например, между двумя параллельными плоскими заряженными проводниками, размеры которых велики по сравнению с расстоянием между ними (рис. 3.2). Напомним, что такая система проводников называется плоским конденсатором. Рис. 3.2. Однородное электрическое поле:1, 2 – параллельные проводники; 3 – эквипотенциальнаяповерхность; 4 – линия напряженностиВ однородном поле очень легко проинтегрировать уравнение (3.6), чтобы получить разность потенциалов между любыми двумя точками 1 и 2. Если учесть, что постоянный вектор напряженности можно вынести за знак интеграла, как любой постоянный множитель, то, интегрируя по произвольному пути L (см. рис. 3.2), получим: (3.12)где – вектор, проведенный от точки 1 к точке 2; – угол между векторами и .Если точки 1 и 2 лежат на одной линии напряженности, то есть векторы и параллельны, то угол  = 0 или 180°, и формула (3.12) превращается в . (3.13)Эта формула позволяет приближенно вычислить напряженность электрического поля в точке, в окрестности которой оно мало отличается от однородного. Достаточно провести через данную точку линию напряженности и измерить вдоль нее расстояние между ближайшими эквипотенциальными поверхностями с потенциалами 1 и 2, после чего найти величину напряженности по формуле (3.14)Экспериментальная установкаИзучение электростатического поля состоит в определении величины и направления вектора напряженности . Но на практике гораздо проще исследовать пространственное распределение потенциалов , построить картину эквипотенциальных поверхностей, и, используя взаимную перпендикулярность линий напряженности и эквипотенциальных поверхностей, воссоздать картину силовых линий электростатического поля.В данной лабораторной работе (рис. 3.3) исследуется квазистационарное электрическое поле, которое возникает в слабопроводящей среде (водопроводная вода), в которую помещены электроды – металлические проводники, подсоединенные к источнику переменного напряжения. Так как проводимость такой среды намного меньше проводимости проводника, то поверхность проводника с большой степенью точности можно считать эквипотенциальной, при этом топография поля в пространстве между электродами будет аналогична топографии электростатического поля заряженных проводников в непроводящей среде. Известно, что водопроводная вода содержит в небольших количествах молекулы солей металлов, которые в электрическом поле распадаются на ионы металлов и ионы оснований, и, в дальнейшем, могут выделяться в виде осадка вблизи электродов. Для исключения такого электролиза используется переменное напряжение U

Проверка справедливости закона ома. определение удельного сопротивления провоЛОКИ

ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ МАГНИТНОГО ПОЛЯ ЗЕМЛИ


МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное
учреждение высшего образования
«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ГЕОСИСТЕМ И ТЕХНОЛОГИЙ»
(СГУГиТ)

ФИЗИКА
МЕХАНИКА. ЭЛЕКТРИЧЕСТВО. МАГНЕТИЗМ

Утверждено редакционно-издательским советом университета

в качестве практикума для обучающихся по всем специальностям и направлениям подготовки

(уровень бакалавриата, уровень специалитета)

Новосибирск

СГУГиТ

2019

УДК 53

Ф503

Авторы: И. Н. Карманов, В. С. Корнеев, Д. С. Михайлова, Д. М. Никулин,
А. С. Сырнева, С. Л. Шергин
Рецензенты: доктор физико-математических наук, профессор НГТУ
В. Я. Костюченко

доктор технических наук, доцент, СГУГиТ В. С. Айрапетян

Ф503 Физика. Механика. Электричество. Магнетизм [Текст] : практикум / И. Н. Карманов, В. С. Корнеев, Д. С. Михайлова, Д. М. Никулин, А. С. Сырнева, С. Л. Шергин ; под общ. ред. И. Н. Карманова. – Новосибирск : СГУГиТ, 2019. – 81 с.

ISBN
Практикум подготовлен на кафедре физики СГУГиТ кандидатом технических наук, доцентом И.Н. Кармановым, кандидатом технических наук, доцентом В.С. Корнеевым, кандидатом технических наук, доцентом С.Л. Шергиным, кандидатом технических наук, доцентом Д.М. Никулиным, старшим преподавателем Д.С. Михайловой, старшим преподавателем А.С. Сырневой.

Содержит описания пяти лабораторных работ: двух – по разделу «Механика», двух – по разделу «Электричество» и одной – по разделу «Магнетизм», выполняемых обучающимися в течение первого семестра изучения дисциплины «Физика». Текст каждой из лабораторных работ содержит краткое теоретическое введение, вопросы для допуска к работе, порядок проведения работы, контрольные вопросы.

Предназначен для обучающихся СГУГиТ всех направлений подготовки и специальностей, изучающих дисциплину «Физика» (уровень бакалавриата, уровень специалитета).

Практикум рекомендован к изданию кафедрой физики СГУГиТ, Ученым советом Института оптики и оптических технологий СГУГиТ.
Печатается по решению редакционно-издательского совета СГУГиТ

УДК 53



ISBN

© СГУГиТ, 2019


СОДЕРЖАНИЕ

Введение 4

1. Лабораторная работа № 1. Определение скорости пули при помощи баллистического маятника 9


2. Лабораторная работа № 2. Определение момента инерции маятника Обербека 23

3. Лабораторная работа № 21. Исследование электростатического поля 44

4. Лабораторная работа № 22. Проверка справедливости закона Ома. Определение удельного сопротивления проволоки 57

5. Лабораторная работа № 41. Определение горизонтальной составляющей магнитного поля Земли 69

Приложение 1. Образец оформления титульного листа 80

Приложение 2. Таблица коэффициентов Стьюдента 81


ВВЕДЕНИЕ

Настоящий лабораторный практикум по физике предназначен для обучающихся СГУГиТ всех форм обучения.

Лабораторный практикум включает в себя введение и описание пяти лабораторных работ, выполняемых обучающимися в течение одного семестра.

Тексты лабораторных работ содержат краткое теоретическое введение, описание лабораторной установки и порядок проведения эксперимента, а также предусматривают перечень вопросов для самоподготовки и контроля знаний по изученным в ходе лабораторной работы темам.

Выполнение обучающимися каждой лабораторной работы, входящей в данный практикум, включает следующие этапы.

  1. Теоретическая подготовка сводится к изучению соответствующих физических явлений и законов для ответа на вопросы для допуска и контрольные вопросы, изучению описания заданной лабораторной работы с целью ознакомления с методикой измерения и порядком выполнения работы. Подготовка проводится заранее, так как аудиторные занятия предназначены только для допуска к работе, проведения измерений, обработки результатов и защиты работы.

  2. Допуск к работе заключается в проверке преподавателем готовности обучающихся к выполнению данной лабораторной работы. Обучающимся необходимо ответить на вопросы для допуска к работе, знать рабочие формулы и порядок выполнения данной лабораторной работы.

  3. Наблюдения и измерения – главная часть эксперимента. Они требуют от обучающегося знания методов измерений, понимания принципа работы лабораторной установки, должного внимания и аккуратности при снятии отчетов и записи результатов измерений.

  4. Обработка результатов измерений заключается в подстановке измеренных параметров в рабочие формулы и вычисление необходимых физических величин в единицах Международной системы единиц (СИ) и оценки погрешностей измерений.

  5. Отчет о выполнении лабораторной работы оформляется индивидуально каждым обучающимся на отдельных листах формата А-4 или на двойных листах в клетку.

Отчет должен содержать следующую информацию:

  1. титульный лист (прил. 1);

  2. цель работы;

  3. приборы и принадлежности;

  4. принципиальная схема или рисунок установки;

  5. рабочие формулы;

  6. таблица результатов измерений и вычислений с учетом математической обработки погрешностей;

  7. графики зависимостей физических величин;

  8. выводы по результатам работы.

  1. Защита лабораторной работы сводится к устному или письменному изложению цели и порядка выполнения лабораторной работы, письменному или устному ответу на вопросы преподавателя, на контрольные вопросы и самостоятельному выводу рабочих формул, используемых в работе.

Обработка результатов измерений

В ходе выполнения лабораторных работ обучающиеся сначала проводят измерение физических величин, а затем вычисление и обработку результатов измерений.

Измерением физической величины называется операция сравнения этой величины с величиной, принятой за эталон. Различают два вида измерений: прямые и косвенные.

Прямыми называют измерения, при которых искомое значение измеряемой величины получают непосредственно, например, каким-либо прибором. Прямым или непосредственным образом можно измерить лишь некоторые физические величины, такие как длина, вес тела, промежутки времени, температура, напряжение, сила тока и др.

Косвенным называют измерение, когда искомое значение физической величины определяется на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной, например, определение мощности постоянного тока по формуле , или из графиков.

Измерения принципиально не могут быть абсолютно точными, а погрешности, возникающие в процессе измерений, делятся на систематические и случайные.

Систематические погрешности возникают вследствие неточности измерительных приборов, недостаточно разработанной методики эксперимента. Величина систематической погрешности одинакова во всех измерениях, проводимых одним и тем же методом, с помощью одних и тех же приборов и не зависит от количества проведенных измерений.


Случайные погрешности являются неизбежным следствием любых измерений и обусловлены: а) неточностью отсчетов по шкале приборов и инструментов; б) неидентичностью условий проведения экспериментов; в) беспорядочными изменениями внешних условий (температуры, давления, силового поля и т. д.), которые невозможно учесть заранее.

Величина случайной погрешности подчиняется, как правило, определенной закономерности. Закон нормального распределения случайных погрешностей впервые сформулировал К. Гаусс.

При обработке результатов измерений, число которых невелико, используется распределение Стьюдента. Необходимо отметить, что если число измерений 50 и более, то распределение Стьюдента переходит в нормальное распределение.

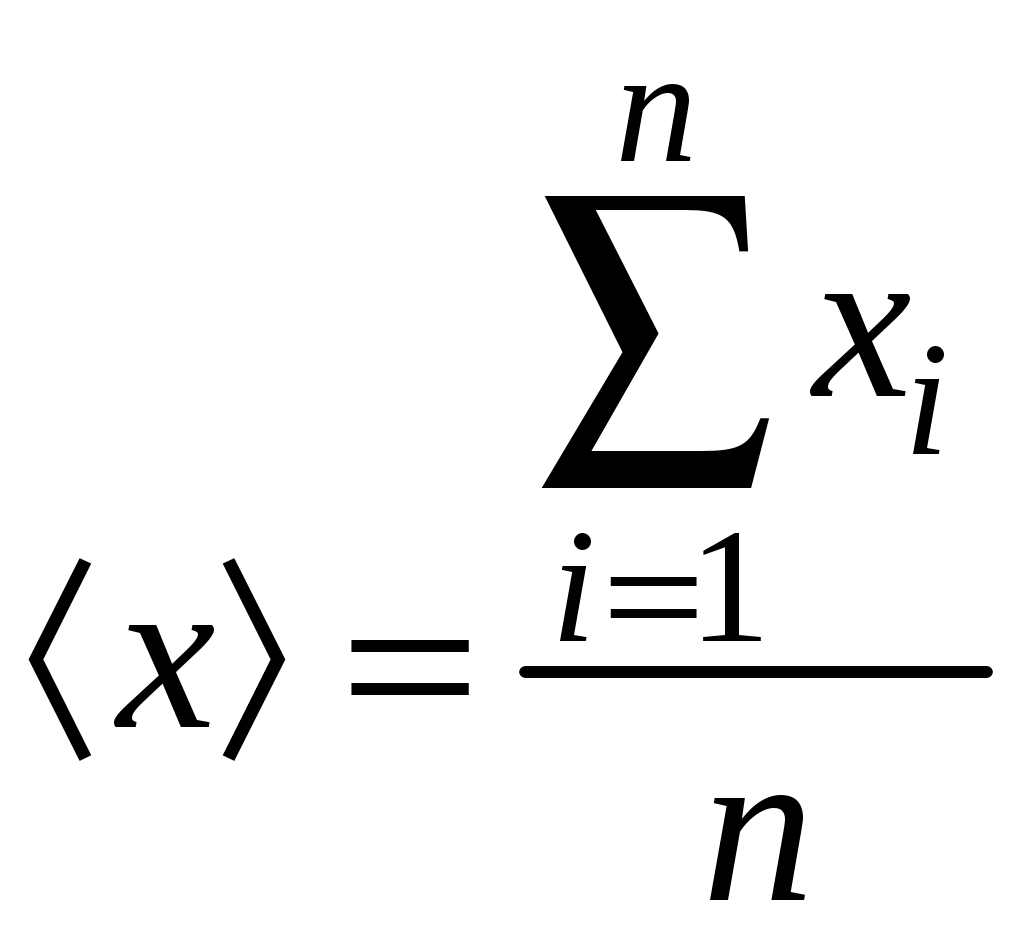Если в результате отдельных измерений некоторой физической величины получен ряд значений этой величины , то наиболее близким к действительному значению измеряемой величины будет – среднее арифметическое значение отдельных измерений:

. (В.1)

Оценить степень приближения среднего арифметического значения к действительному значению измеряемой величины можно по абсолютной погрешности измерений – .

Зная абсолютную погрешность, можно указать доверительный интервал или , в котором находится истинное значение искомой величины .

Величина доверительного интервала зависит от требуемой степени надежности измерений –
. Надежностью измерений называется вероятность того, что искомая величина попадает в указанный доверительный интервал. Надежность или доверительная вероятность обычно выражается в долях единицы, либо в процентах.

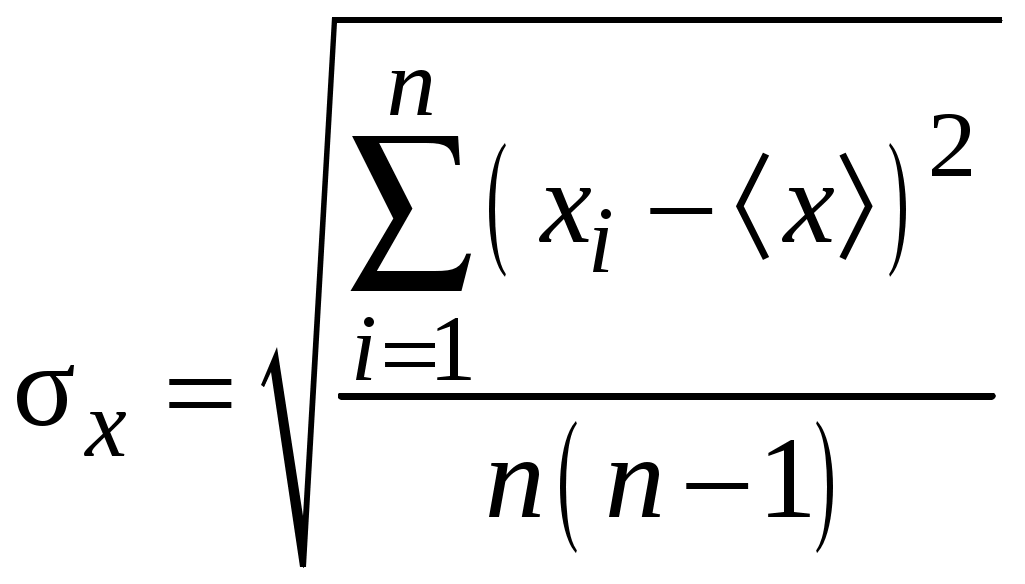Если выполнено измерений некоторой физической величины  средняя квадратичная погрешность определяется из следующего выражения:

. (В.2)

Задача обработки результатов состоит в том, чтобы определить случайную погрешность измерений по заданной заранее надежности измерений .

, (В.3)

где – коэффициент Стьюдента, численное значение которого при заданных значениях и можно определить из справочных таблиц (прил. 2).

Таким образом, устанавливается следующий порядок обработки результатов:

  1. вычисление среднего арифметического значения по формуле (В.1);

  2. вычисление средней квадратичной погрешности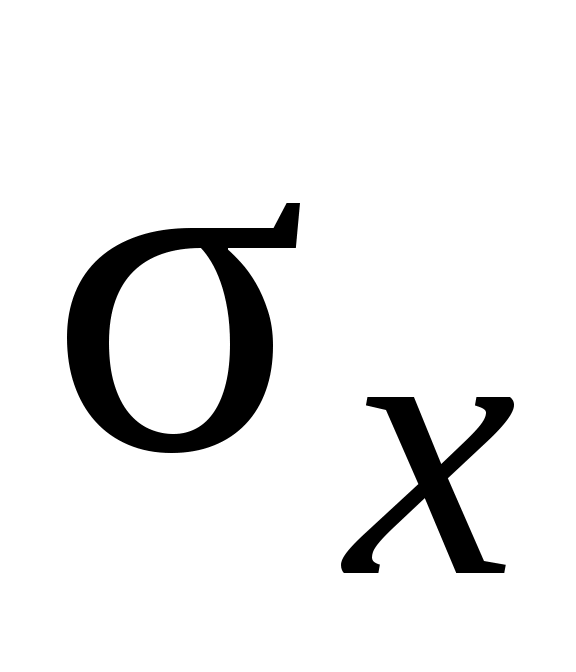 по формуле (В.2);

  3. определение коэффициента Стьюдента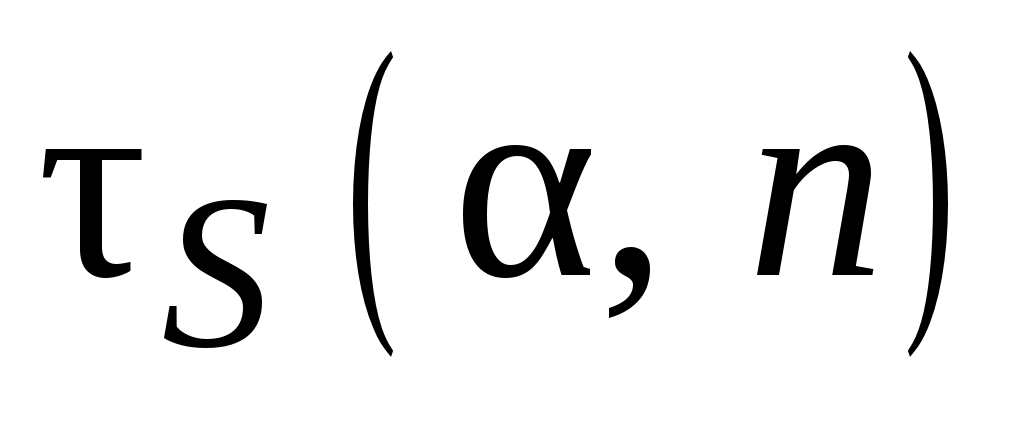 с учетом числа измерений и заданной надежности ;

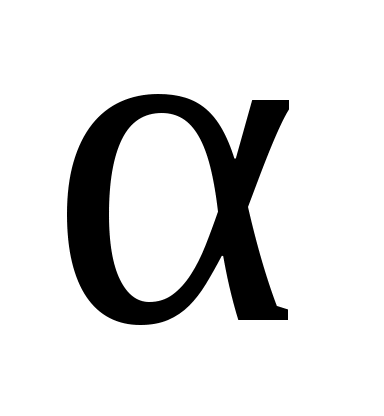  4. расчет случайной погрешности по формуле (В.3).

Смотрите также файлы