ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 154
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Rопределяется разностным методом:
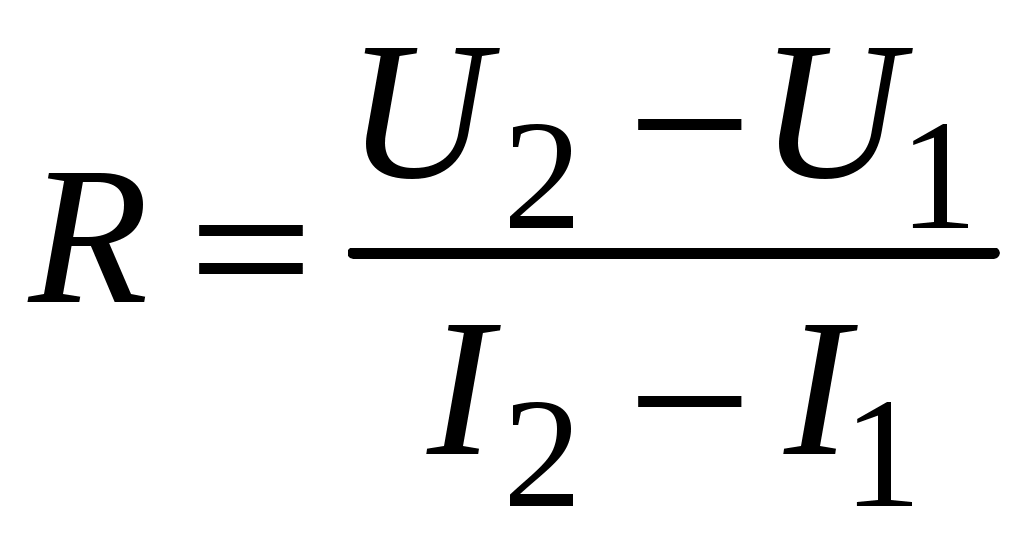 . (4.12)
. (4.12)
При этом методе влияние систематических ошибок измерения напряжения и силы тока будет минимально.
Задание 3
Определение удельного сопротивления проводника
Как следует из формулы (4.8), сопротивление проводника линейно зависит от его длины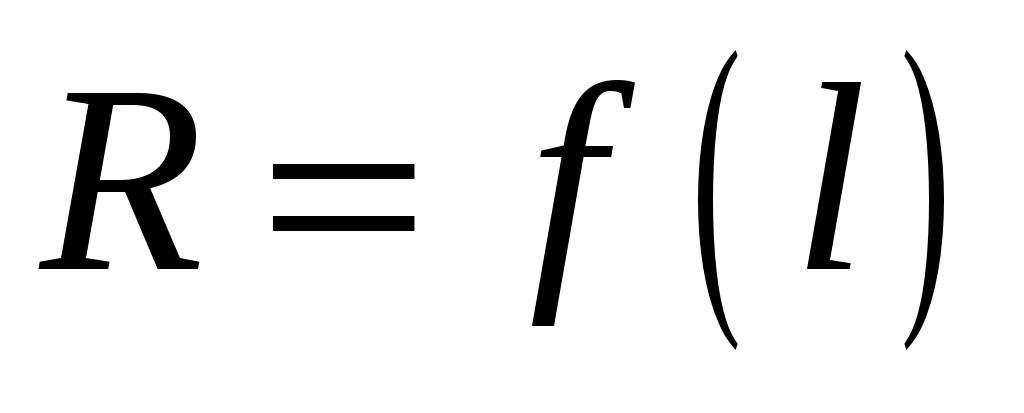 . Поэтому для определения удельного сопротивления проводника
. Поэтому для определения удельного сопротивления проводника 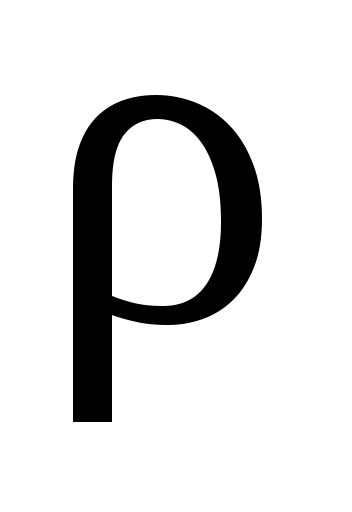 необходимо по методике второго задания определить сопротивления проводника
необходимо по методике второго задания определить сопротивления проводника 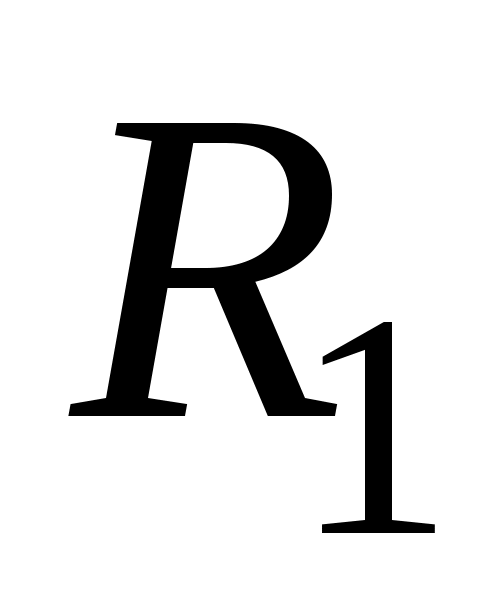 и
и 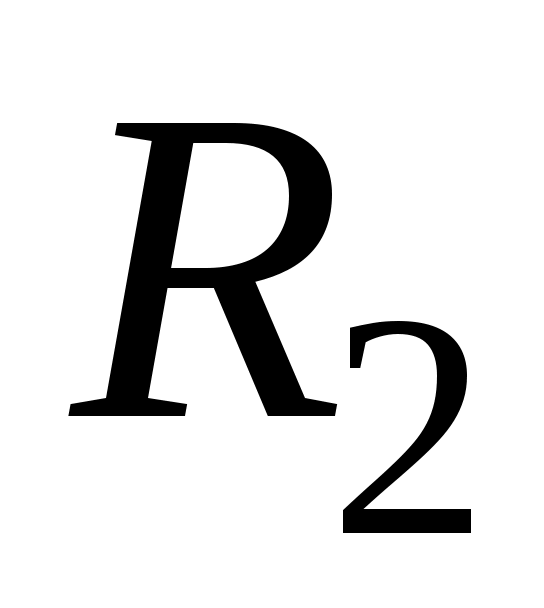 при разных длинах
при разных длинах 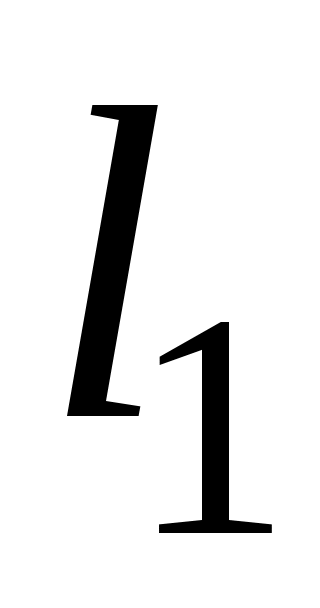 и
и 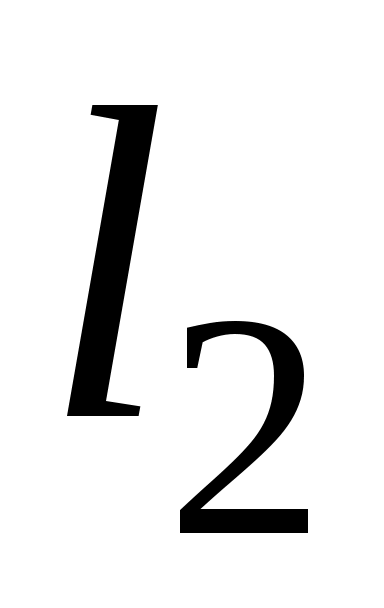 .
.
Удельное сопротивление определяется по следующей формуле:
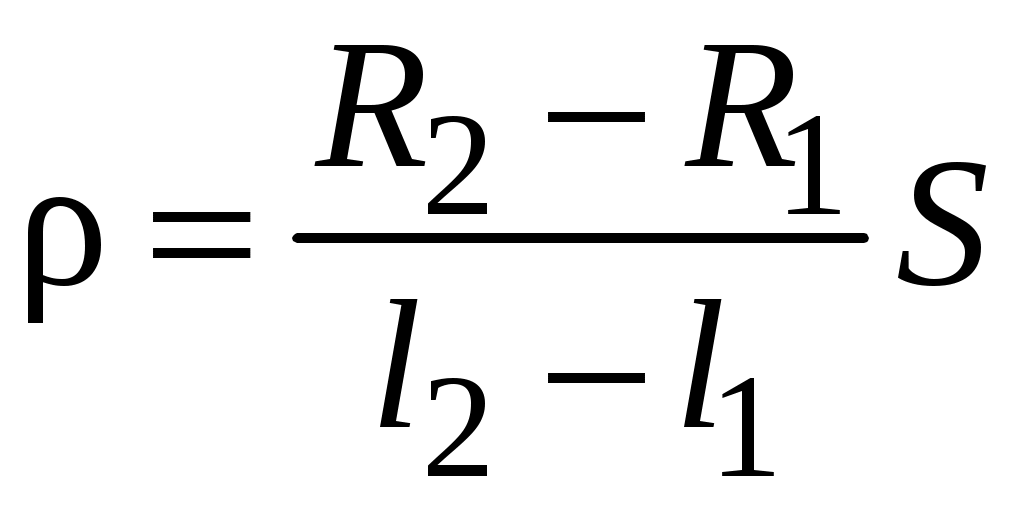 . (4.13)
. (4.13)
В табл. 4.1 приведены значения удельных сопротивлений некоторых распространенных металлов и сплавов.
Таблица 4.1
Порядок выполнения лабораторной работы
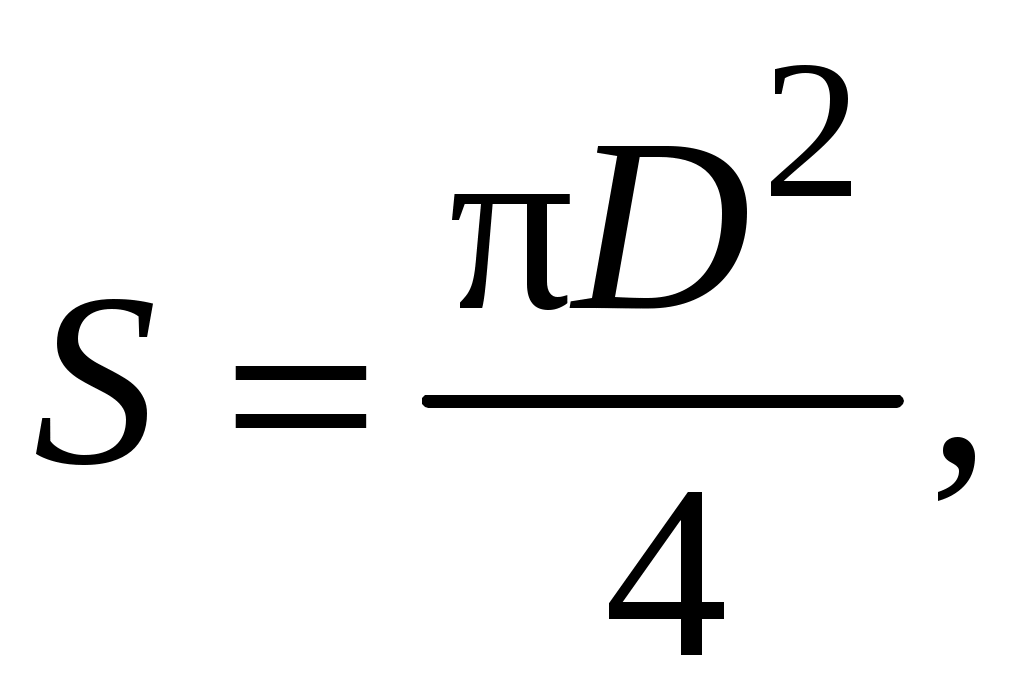
где D диаметр сечения проволоки, указанный на корпусе прибора.
Таблица 4.2
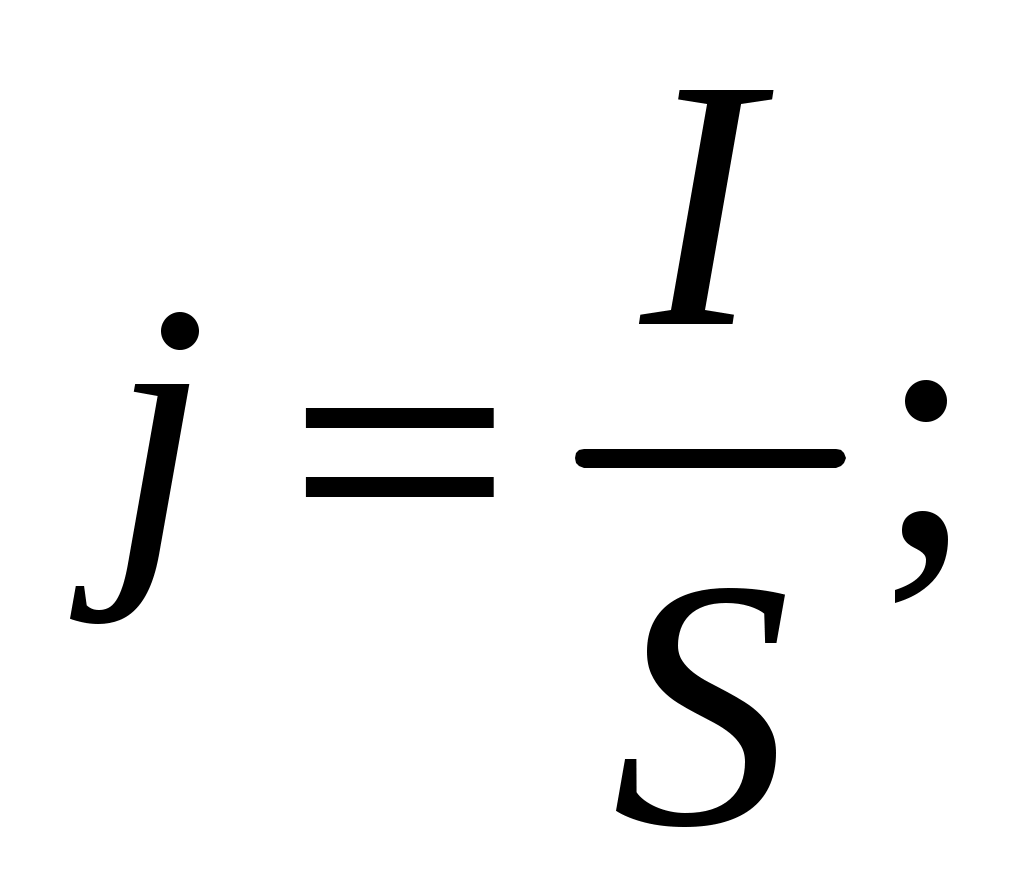
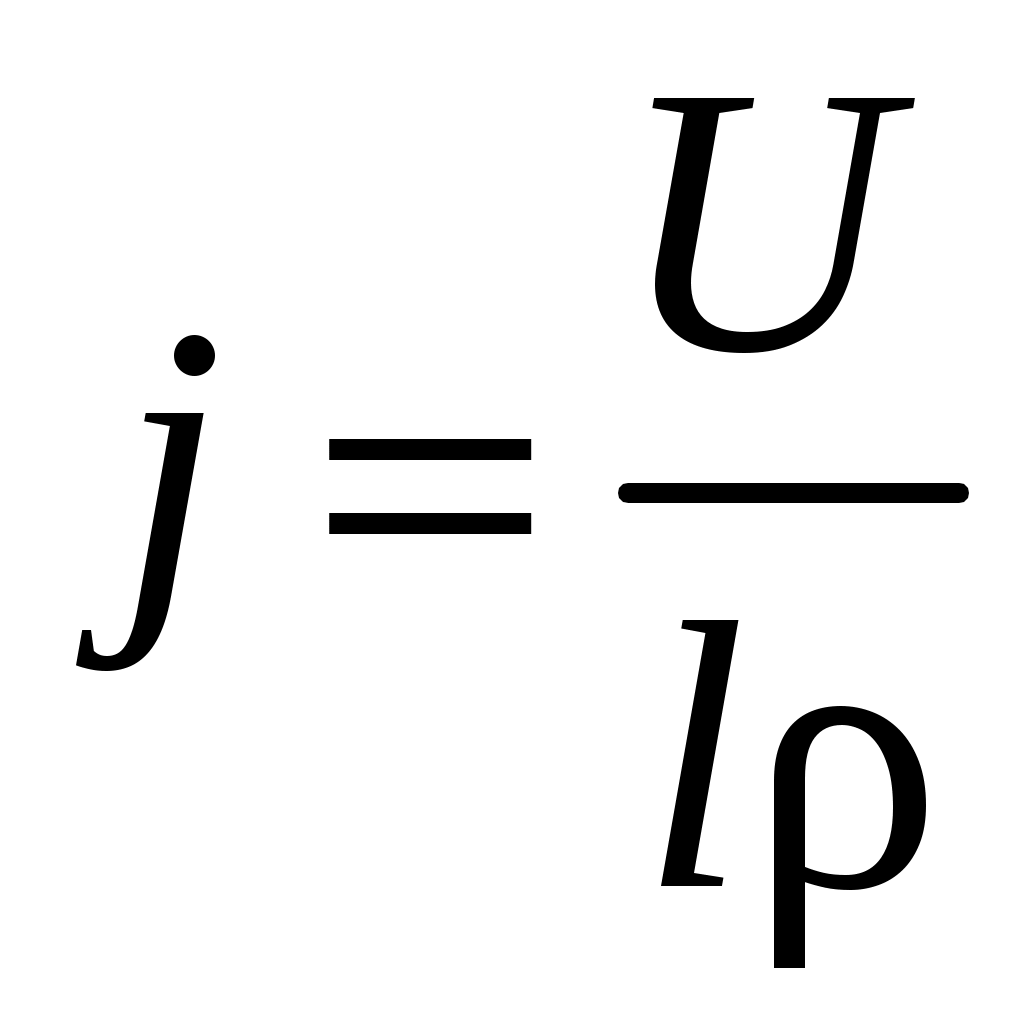
и сравните полученные результаты.
Контрольные вопросы
Список литературы
5. Лабораторная работа № 41
Цель работы
Экспериментально определить горизонтальную составляющую вектора напряженности магнитного поля Земли.
Приборы и принадлежности
Лабораторная установка «Тангенс-гальванометр» с катушками Гельмгольца, источником и регулятором постоянного тока.
Подготовка к работе
По лекциям и приведенному ниже списку литературы изучите следующие вопросы:
Вопросы для допуска к работе
Теоретическое введение
В пространстве, окружающем электрические токи и постоянные магниты, возникает силовое поле, называемое магнитным. Оно обнаруживается по силовому действию на внесенные в него проводники с током или на намагниченные тела. Силовой характеристикой этого магнитного поля является вектор магнитной индукции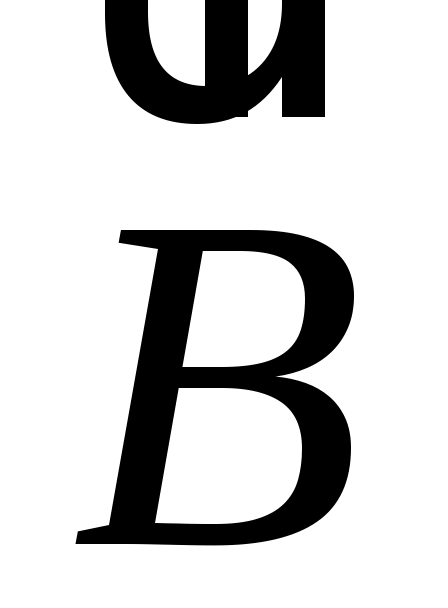 .
.
Магнитное поле изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора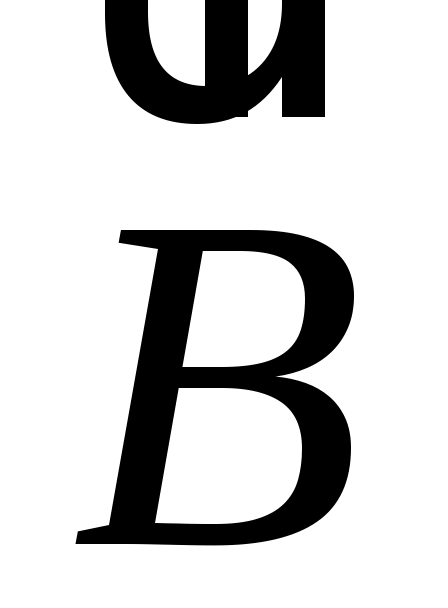 . Линии магнитной индукции всегда замкнуты и охватывают проводники с током, этим они отличаются от линий напряженности электростатического поля. Замкнутость линий индукции обусловлена отсутствием в природе «магнитных зарядов».
. Линии магнитной индукции всегда замкнуты и охватывают проводники с током, этим они отличаются от линий напряженности электростатического поля. Замкнутость линий индукции обусловлена отсутствием в природе «магнитных зарядов».
Магнитное поле в пространстве могут создавать как макротоки (токи, текущие в проводниках), так и микротоки (атомные и молекулярные токи в магнитных материалах). Поэтому вектор магнитной индукции характеризует результирующее магнитное поле.
характеризует результирующее магнитное поле.
Вектор напряженности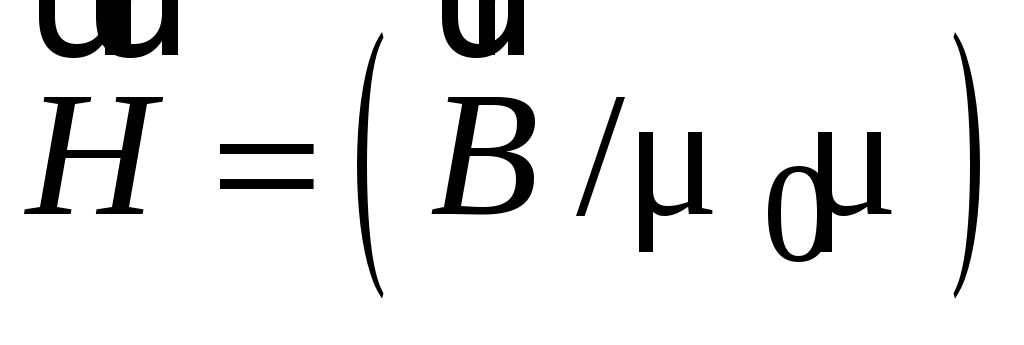 количественно характеризует поле макротоков (
количественно характеризует поле макротоков (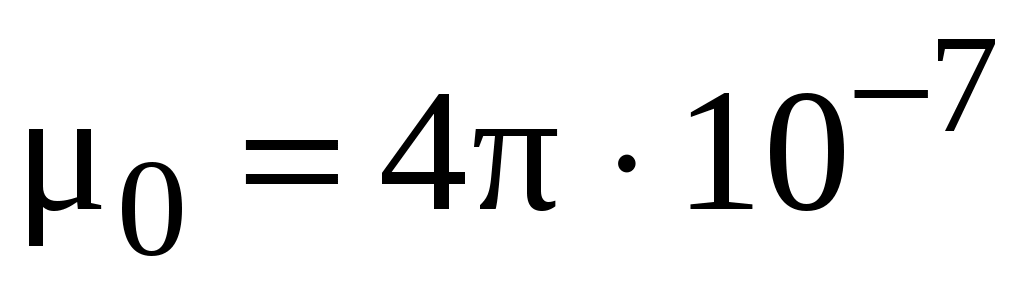 Гн/м – магнитная постоянная;
Гн/м – магнитная постоянная; 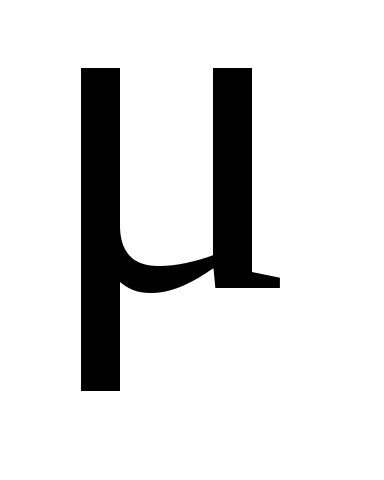 – магнитная проницаемость среды).
– магнитная проницаемость среды).
Закон Био – Савара – Лапласа позволяет определить магнитную индукцию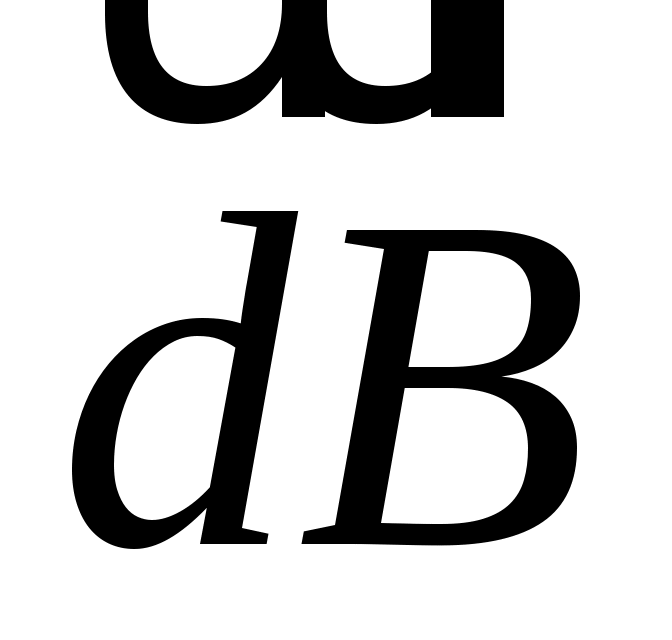 , создаваемую малым однородным элементом
, создаваемую малым однородным элементом  проводника с током
проводника с током 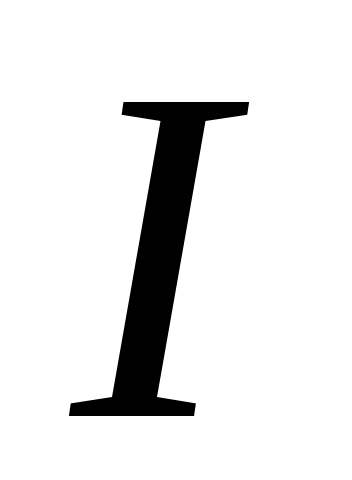 на расстоянии
на расстоянии 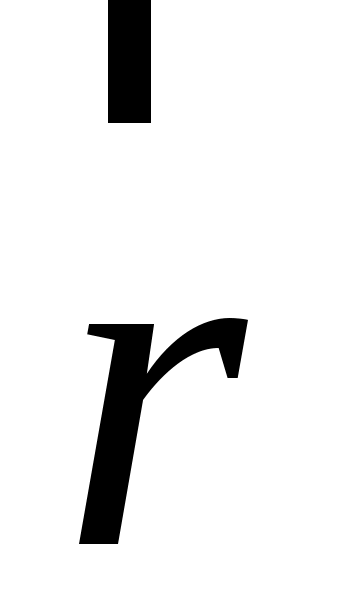 от него. Этот закон может быть записан в векторной и скалярной формах:
от него. Этот закон может быть записан в векторной и скалярной формах:
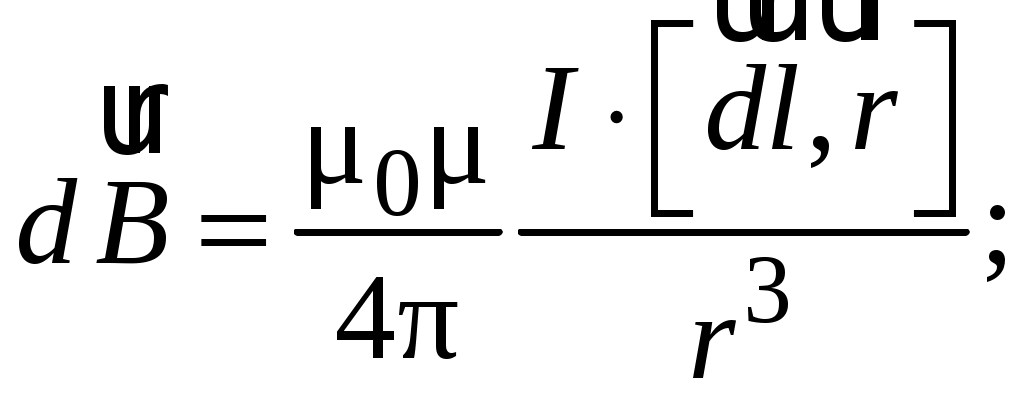 (5.1)
(5.1)
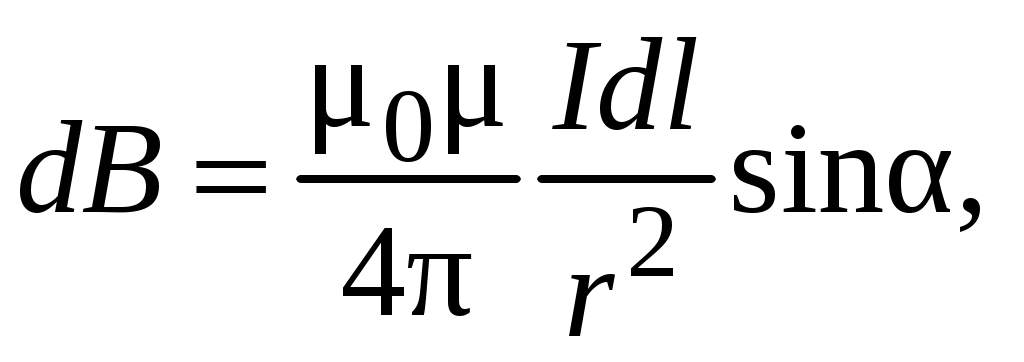 (5.2)
(5.2)
где – угол между векторами
– угол между векторами  и
и 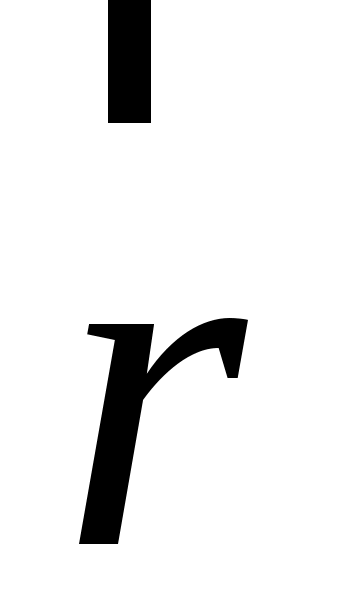 , вектор
, вектор  равен по модулю длине участка проводника и совпадает по направлению с током (рис. 5.1).
равен по модулю длине участка проводника и совпадает по направлению с током (рис. 5.1).
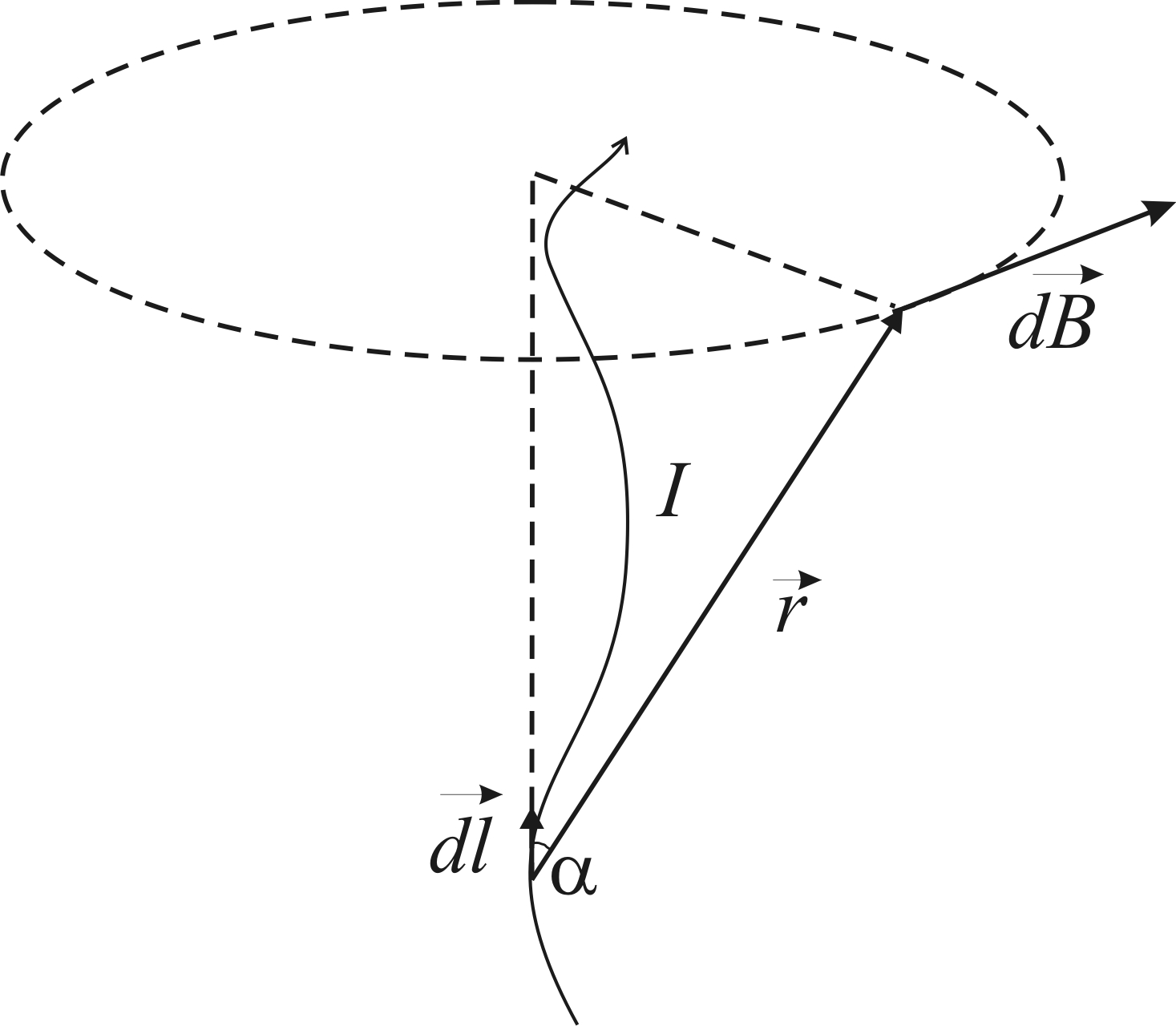
Рис. 5.1. Взаимное расположение в пространстве векторов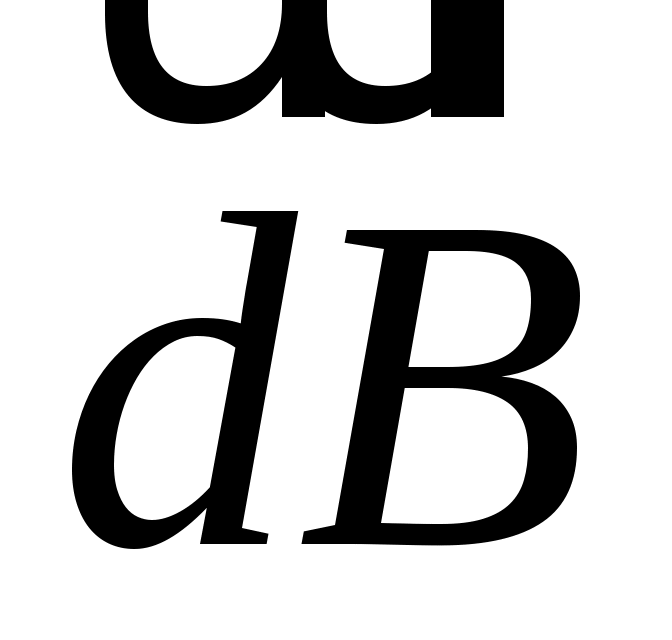 ,
,  и
и 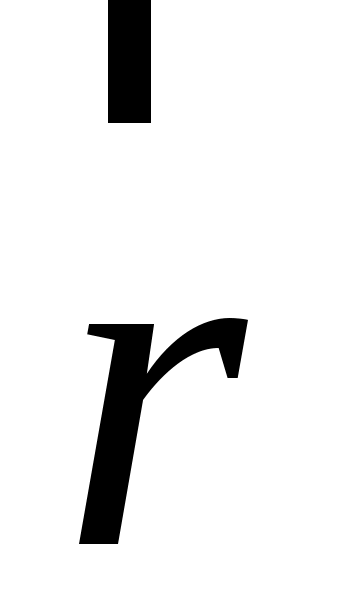
Для того чтобы определить в некоторой точке магнитную индукцию
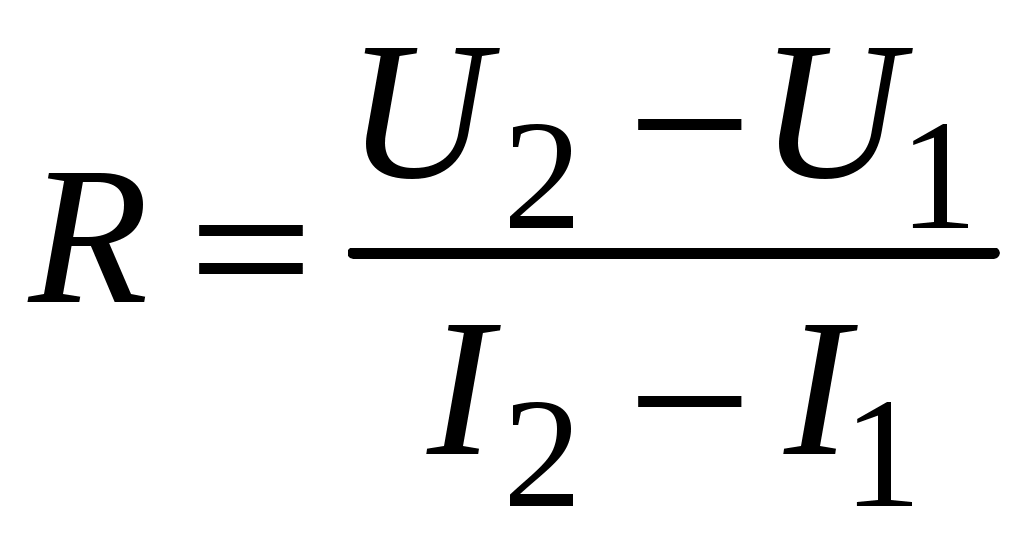 . (4.12)
. (4.12)При этом методе влияние систематических ошибок измерения напряжения и силы тока будет минимально.
Задание 3
Определение удельного сопротивления проводника
Как следует из формулы (4.8), сопротивление проводника линейно зависит от его длины
Удельное сопротивление определяется по следующей формуле:
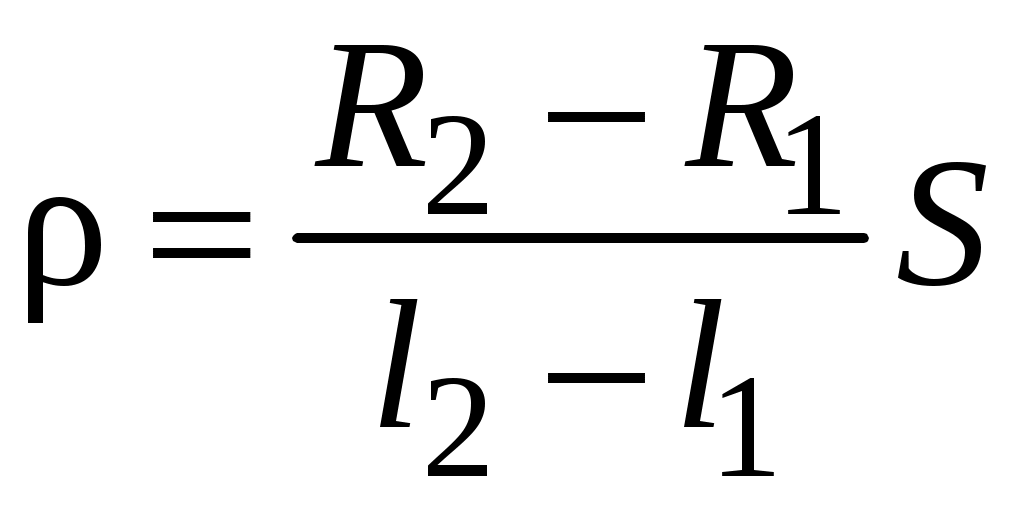 . (4.13)
. (4.13)В табл. 4.1 приведены значения удельных сопротивлений некоторых распространенных металлов и сплавов.
Таблица 4.1
| Металл | при | Сплав | при |
| 1. Медь | 0,017 | 6. Хромель | 0,66 |
| 2. Алюминий | 0,027 | 7. Нихром | 1,1 |
| 3. Железо | 0,097 | 8. Хромаль | 1,5 |
| 4. Свинец | 0,2 | 9. Алюмель | 3 |
| 5. Титан | 0,55 | 10. Копель | 4,6 |
Порядок выполнения лабораторной работы
-
Составьте таблицу для записи результатов измерения напряжения U и тока I (табл. 4.2) -
Определите площадь сечения проволоки по формуле:
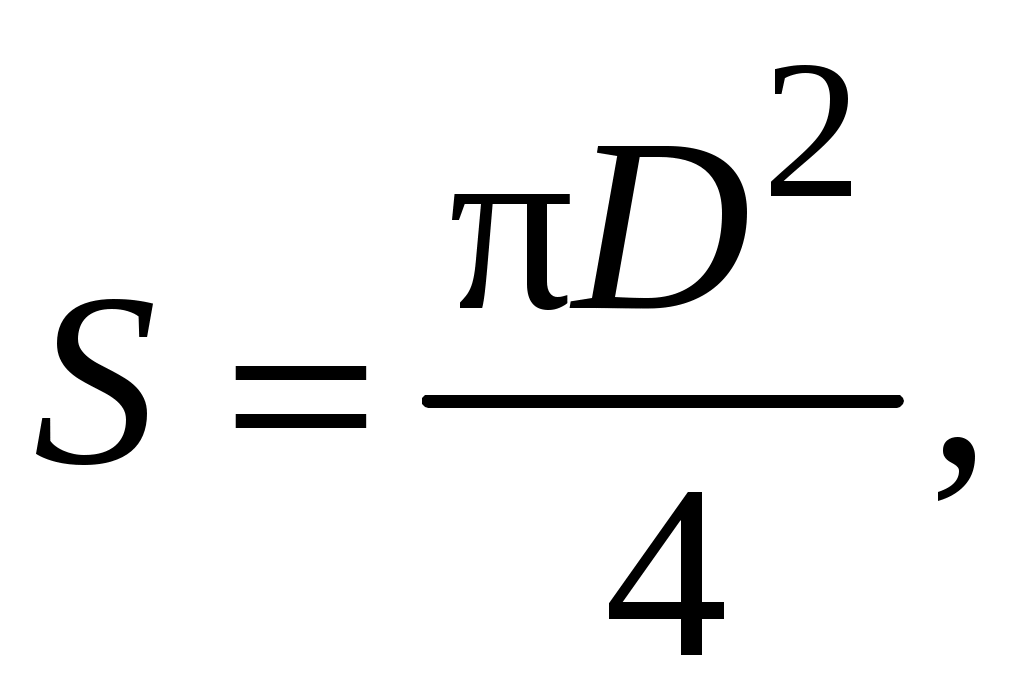
где D диаметр сечения проволоки, указанный на корпусе прибора.
-
С помощью ползунка на кронштейне установите длину проволоки l. Включите прибор в сеть. Изменяя силу тока, снимите зависимость U= U(I) (не менее четырех точек). Результаты занесите в табл. 4.2.
Таблица 4.2
| № | l (м) | I(А) | U(В) | R (Ом) | ρ (Ом·м) |
| 1 | | | | | |
| | | ||||
| | | ||||
| | | ||||
| 2 | | | | | |
| | | ||||
| | | ||||
| | |
-
Повторите измерения п. 3 для другого значения длины проволоки l. -
Постройте графики зависимостей напряжения от силы тока для двух длин l1 и l2 и убедитесь в прямой пропорциональности значений U и I. -
Определите удельное сопротивление проводника по формуле (4.13) и по данным табл. 4.1 определите материал, из которого изготовлена проволока.
проводника по формуле (4.13) и по данным табл. 4.1 определите материал, из которого изготовлена проволока. -
Взяв необходимые данные из табл. 4.2, проведите расчеты значений плотности тока, протекающего по проводнику, по формулам:
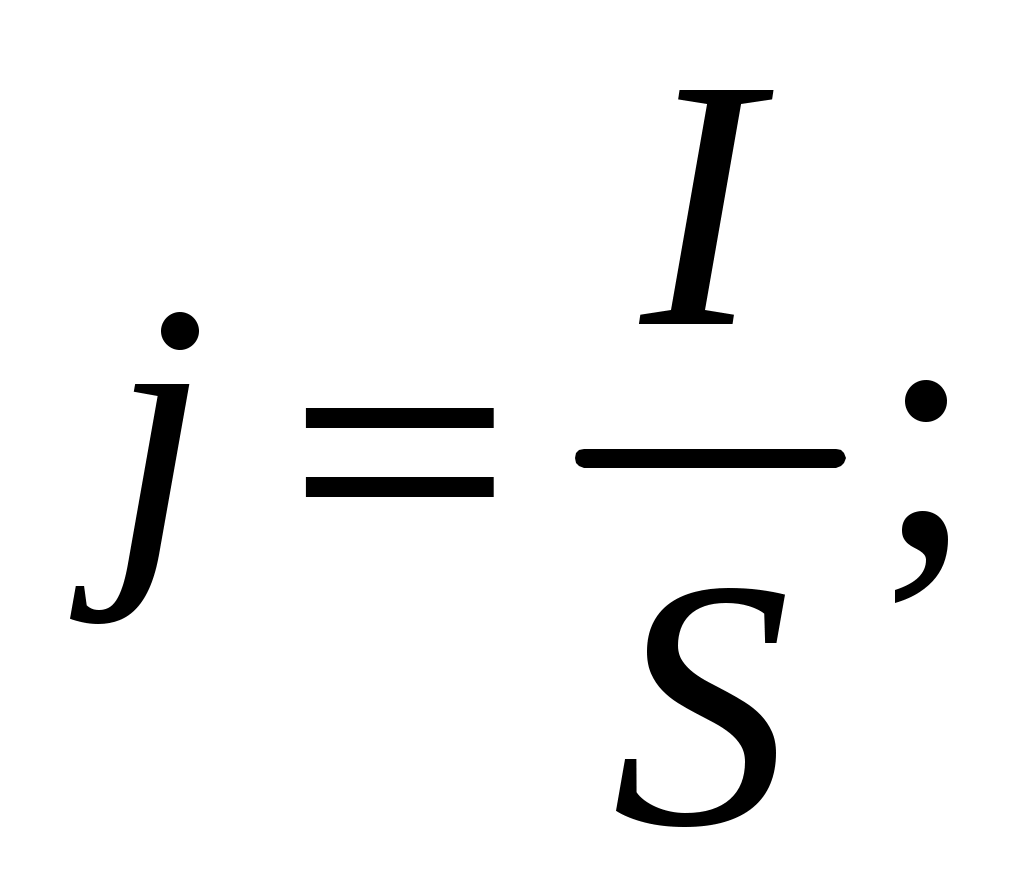
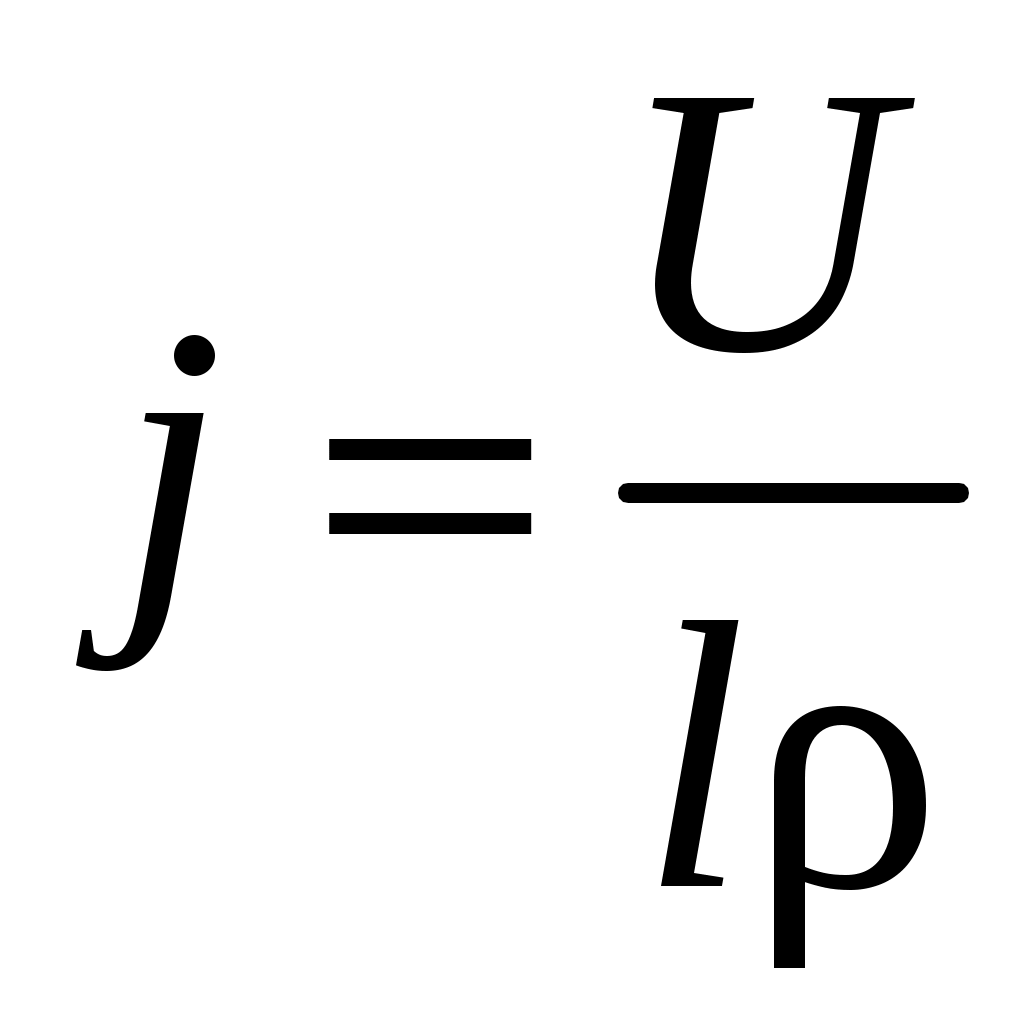
и сравните полученные результаты.
Контрольные вопросы
-
По результатам выполнения задания № 1 обоснуйте, какая из измерительных схем дает меньшую погрешность. -
Дайте определение силы тока. В каких единицах она измеряется? -
Запишите закон Ома для однородного участка цепи. -
Объясните роль источников ЭДС в электрических цепях. -
Что такое сопротивление проводника? В каких единицах оно измеряется? -
От каких физических величин зависит сопротивление проводника? -
Как вычисляется сопротивление проводников при параллельном и последовательном соединении? -
Запишите закон Ома в дифференциальной форме.
Список литературы
-
Трофимова Т. И. Курс физики : учеб. пособие. – М. : Академия, 2015. – 560 с. -
Тюшев А. Н., Вайсберг А. И. Курс лекций по физике : учеб. пособие. – 2-е изд., испр. и доп. Ч. 2. Электричество и магнетизм. – Новосибирск : СГГА, 2011. – 175 с. -
Савельев И. В. Курс общей физики. В 3 т. Т. 2. Электричество и магнетизм. Волны. Оптика [Электронный ресурс] : учеб. пособие. – СПб. : Лань, 2016. – 500 с. – Режим доступа : http://e.lanbook.com/ books/element. php? pl1_id=71761.
5. Лабораторная работа № 41
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
Цель работы
Экспериментально определить горизонтальную составляющую вектора напряженности магнитного поля Земли.
Приборы и принадлежности
Лабораторная установка «Тангенс-гальванометр» с катушками Гельмгольца, источником и регулятором постоянного тока.
Подготовка к работе
По лекциям и приведенному ниже списку литературы изучите следующие вопросы:
-
магнитное поле и его характеристики; -
закон Био – Савара – Лапласа, -
принцип суперпозиции магнитных полей; -
магнитное поле витка с током; -
магнитное поле Земли и его составляющие.
Вопросы для допуска к работе
-
Как связаны между собой индукция и напряженность магнитного поля в среде (например, в воздухе)? -
Чему равна напряженность магнитного поля между катушками Гельмгольца на оси системы в точке, равноудаленной от обеих катушек? -
Укажите составляющие магнитного поля Земли. -
Изложите методику определения горизонтальной составляющей магнитного поля Земли. -
Как изменяются составляющие магнитного поля Земли при переходе от экватора к полюсам?
Теоретическое введение
В пространстве, окружающем электрические токи и постоянные магниты, возникает силовое поле, называемое магнитным. Оно обнаруживается по силовому действию на внесенные в него проводники с током или на намагниченные тела. Силовой характеристикой этого магнитного поля является вектор магнитной индукции
Магнитное поле изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора
Магнитное поле в пространстве могут создавать как макротоки (токи, текущие в проводниках), так и микротоки (атомные и молекулярные токи в магнитных материалах). Поэтому вектор магнитной индукции
Вектор напряженности
Закон Био – Савара – Лапласа позволяет определить магнитную индукцию
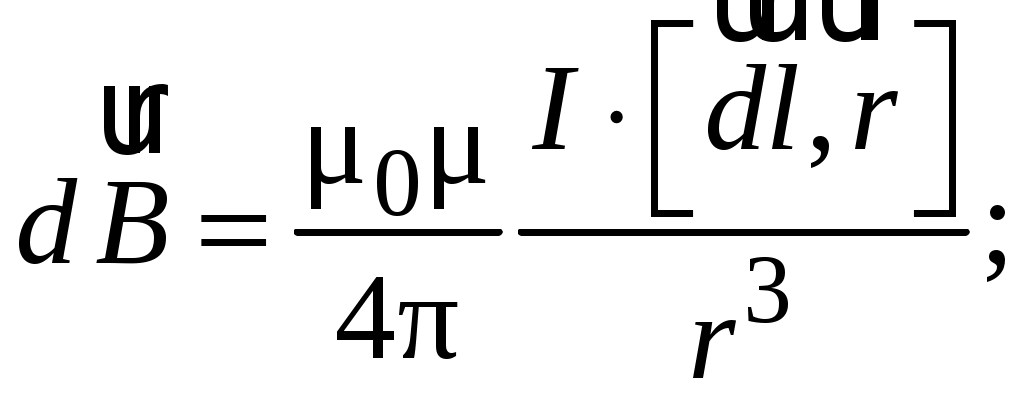 (5.1)
(5.1)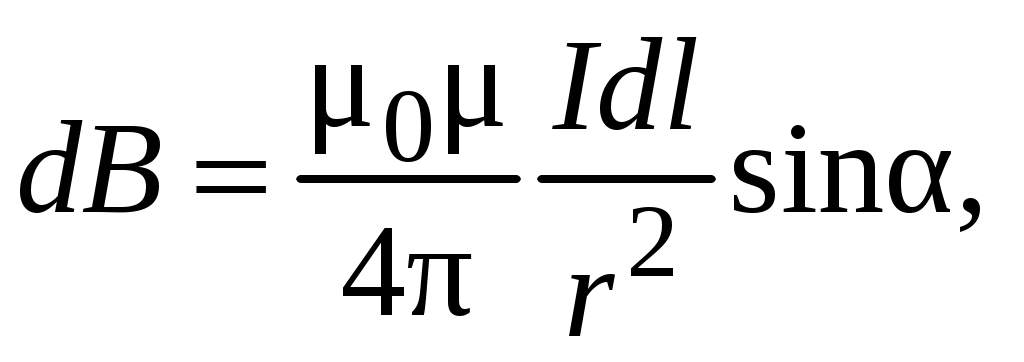 (5.2)
(5.2)где

Рис. 5.1. Взаимное расположение в пространстве векторов
Для того чтобы определить в некоторой точке магнитную индукцию