ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 151
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
с максимальным отклонением маятника. На рис. 1.2 изображена система «пуля – маятник» в трех важных для установления этой связи состояниях.
Состояние 1 – пуля вылетела из пистолета, но еще не долетела до цилиндра. Цилиндр неподвижен.
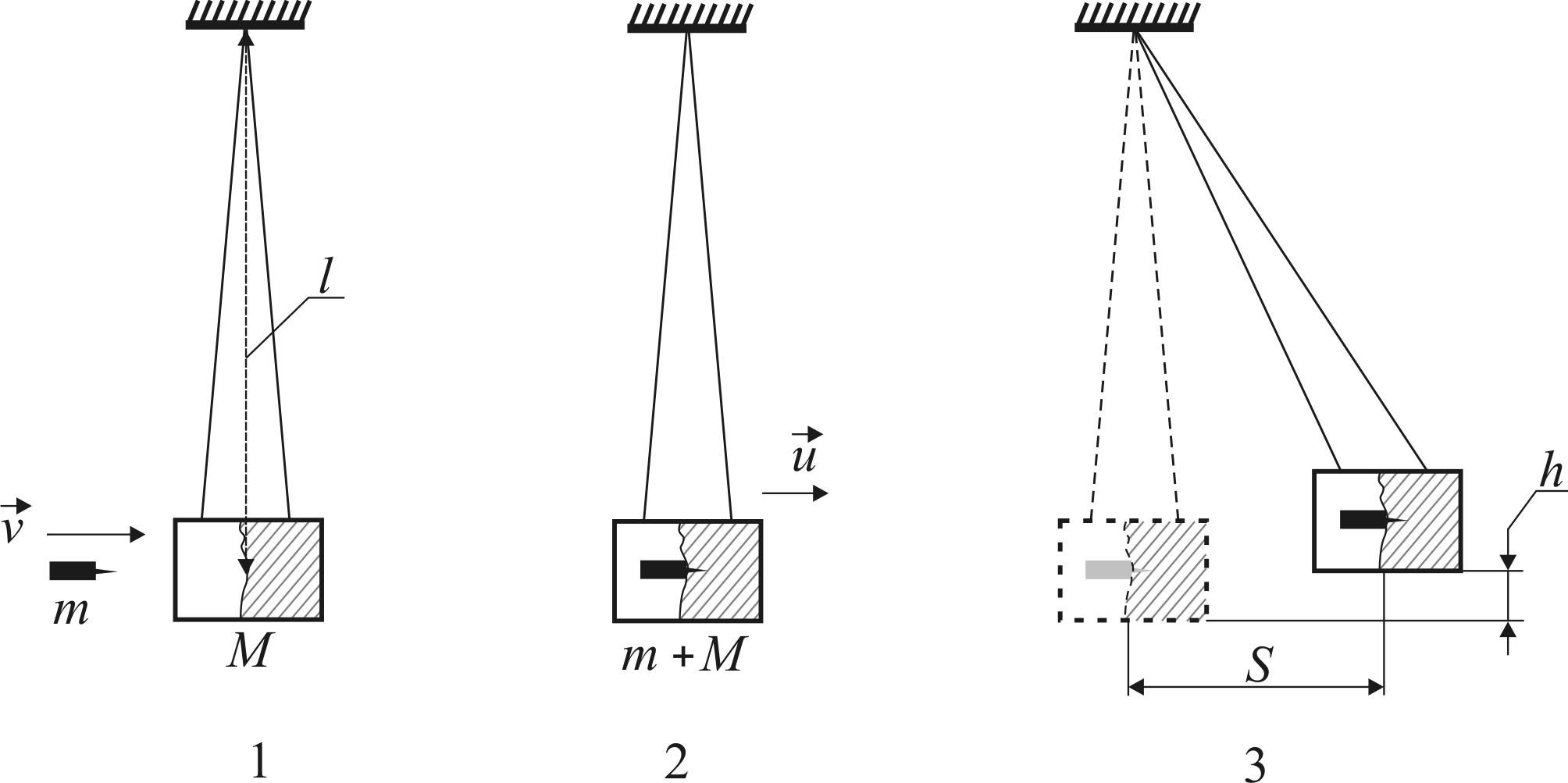
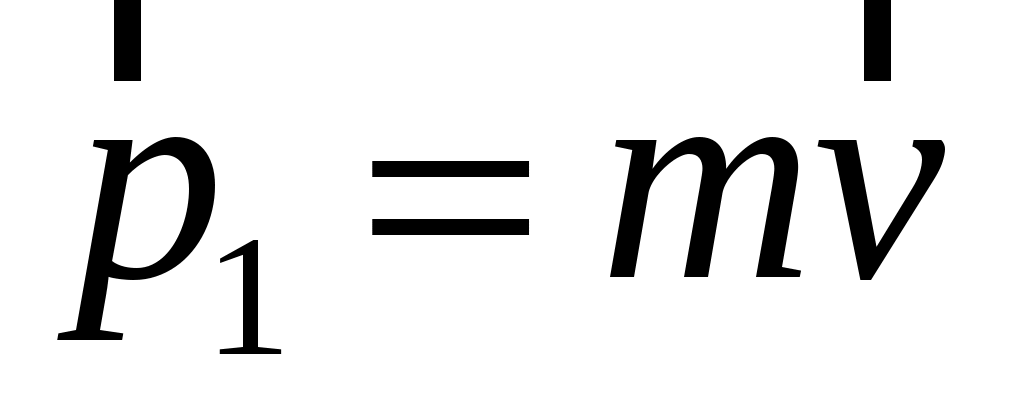
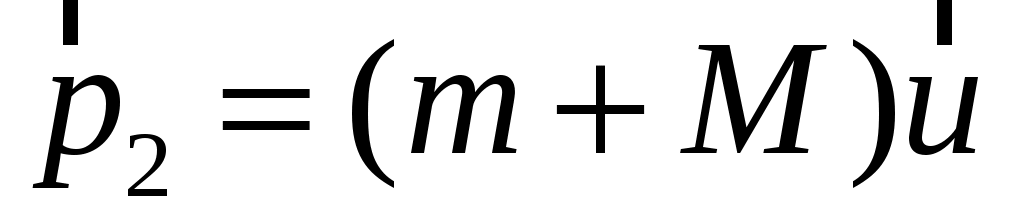

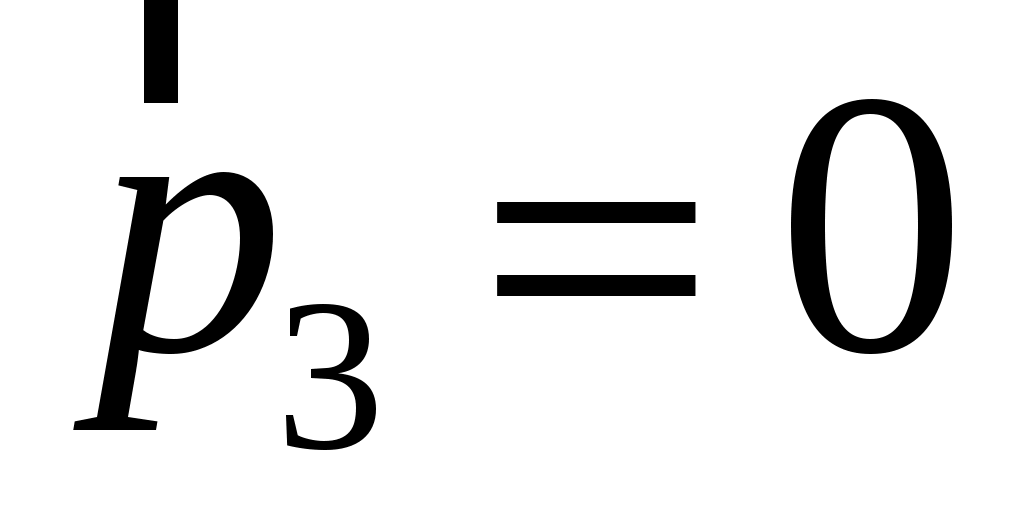
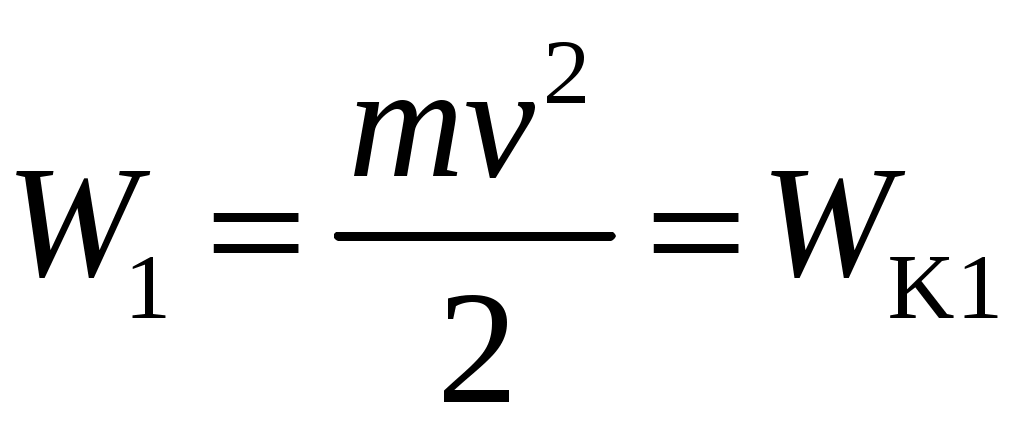
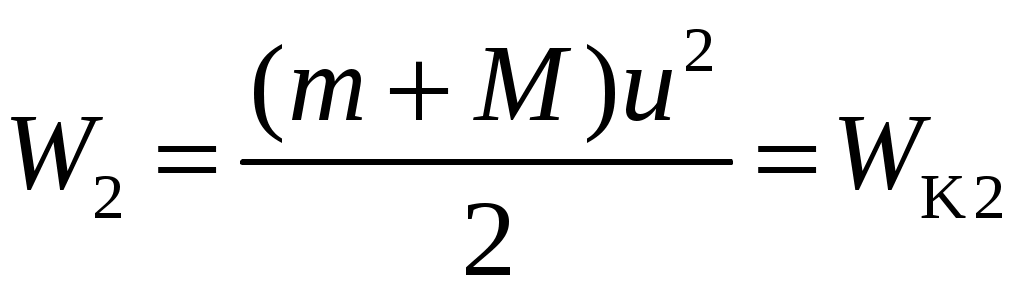
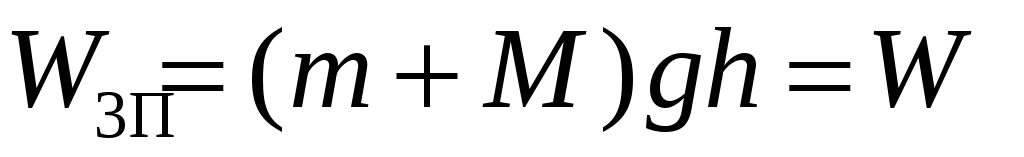
Рис. 1.2. Импульс и механическая энергия маятника в трех состояниях
Состояние 2 – пуля попала в цилиндр, цилиндр вместе с пулей начали движение со скоростью u, отклонение маятника приближенно равно нулю.
Состояние 3 – маятник отклонился на максимальный угол.
В процессе перехода системы из первого состояния во второе (процесс 1-2) сохраняется проекция полного импульса системы на горизонтальную ось, так как в момент удара горизонтальных внешних сил нет (сопротивлением воздуха пренебрегаем). Таким образом, горизонтальная проекция полного импульса системы до попадания пули в маятник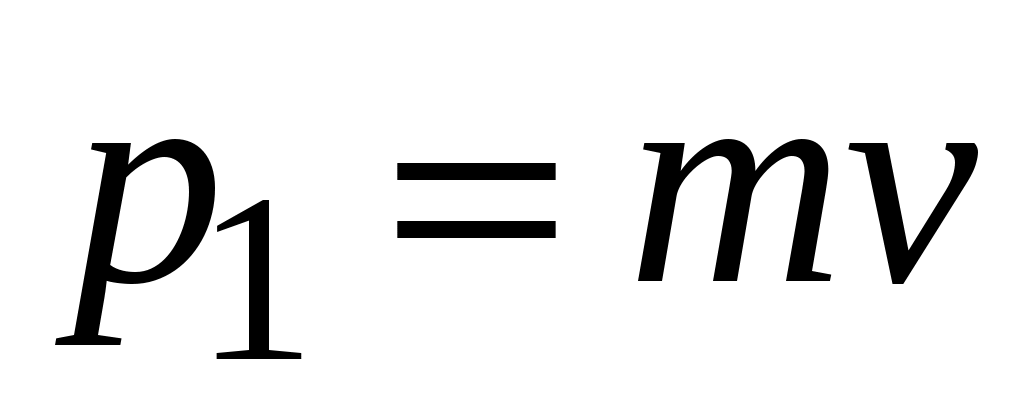 будет равна горизонтальной проекции полного импульса системы
будет равна горизонтальной проекции полного импульса системы 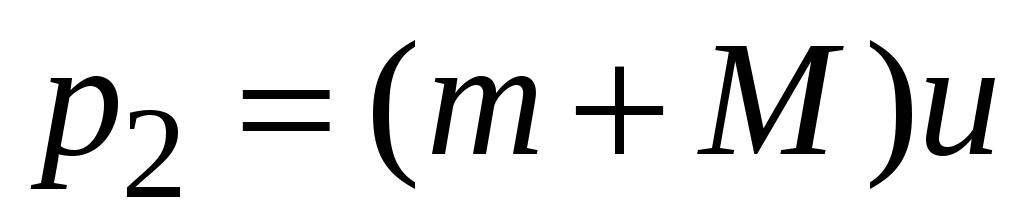 сразу после попадания пули в маятник:
сразу после попадания пули в маятник:
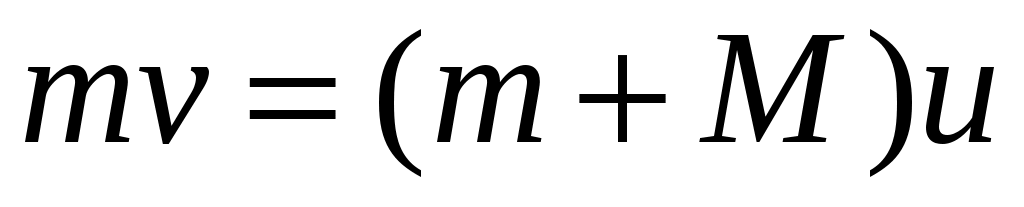 . (1.2)
. (1.2)
Таким образом, закон сохранения импульса связывает состояние 1 и состояние 2. Полная механическая энергия системы «пуля – маятник» в процессе 1-2 не сохраняется, так как при движении пули в пластилине действуют неконсервативные силы (силы трения и силы, возникающие при неупругой деформации пластилина).
Убыль механической энергии равна работе неконсервативных сил и, в конечном итоге, выделившемуся в системе теплу:
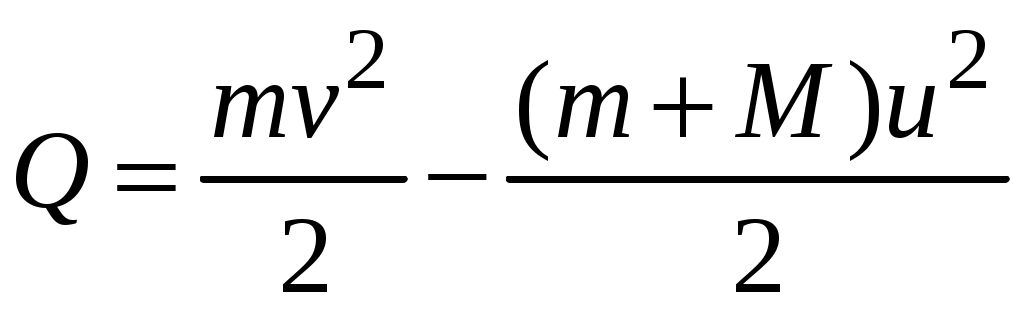
. (1.3)
В процессе 2-3 (перехода из второго состояние в третье) неконсервативные силы отсутствуют (сопротивлением воздуха и трением в подвесе можно пренебречь), поэтому к процессу 2-3 можно применить закон сохранения полной механической энергии:
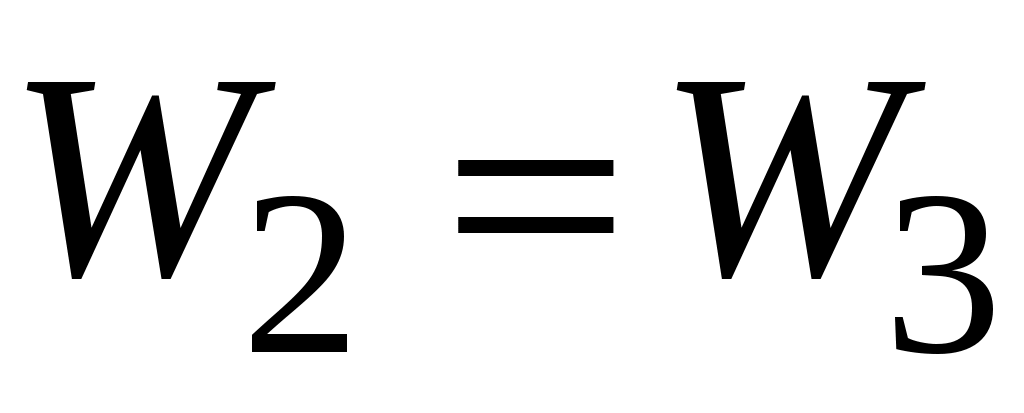 ,
,
где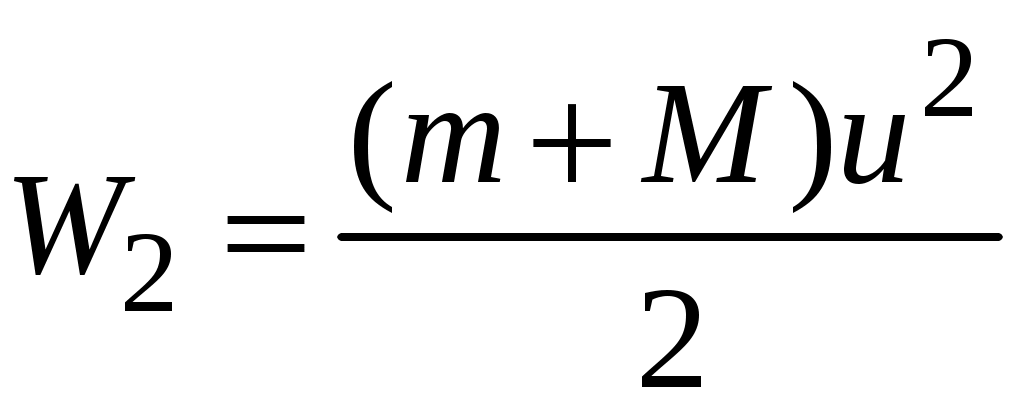 – полная механическая энергия системы «пуля – маятник» в состоянии 2;
– полная механическая энергия системы «пуля – маятник» в состоянии 2;
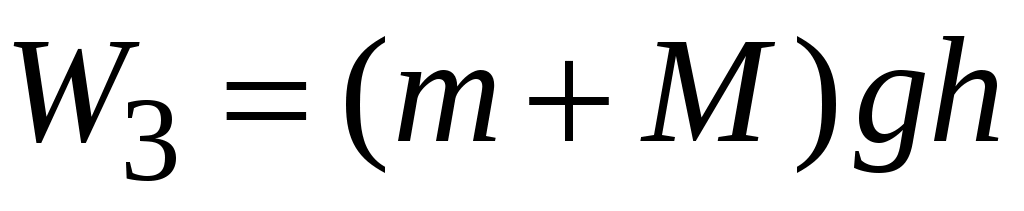 – полная механическая энергия системы «пуля – маятник» в состоянии 3.
– полная механическая энергия системы «пуля – маятник» в состоянии 3.
Приравнивая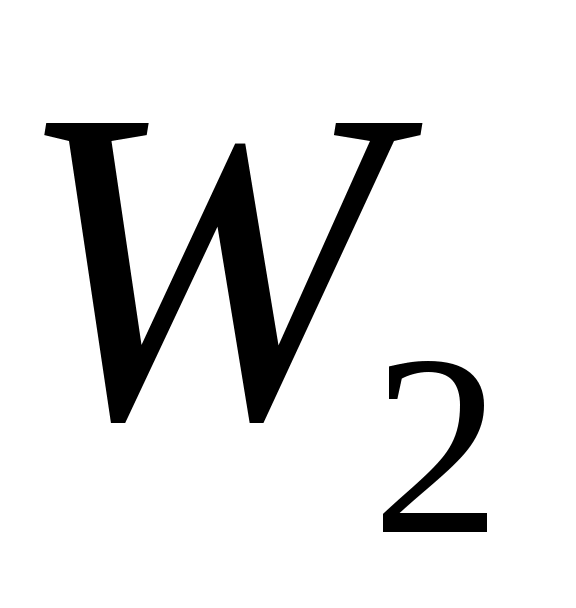 и
и  , получим:
, получим:
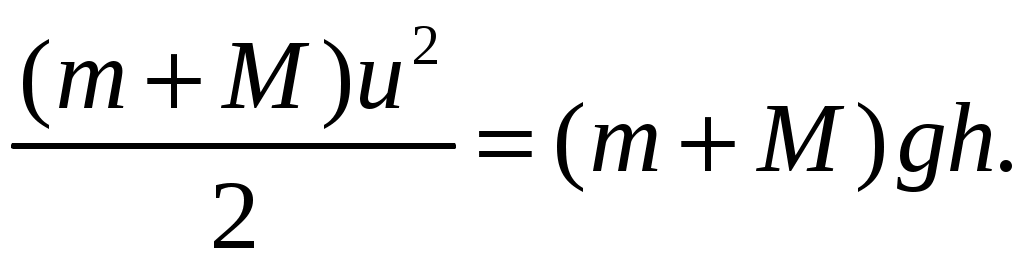
После сокращения на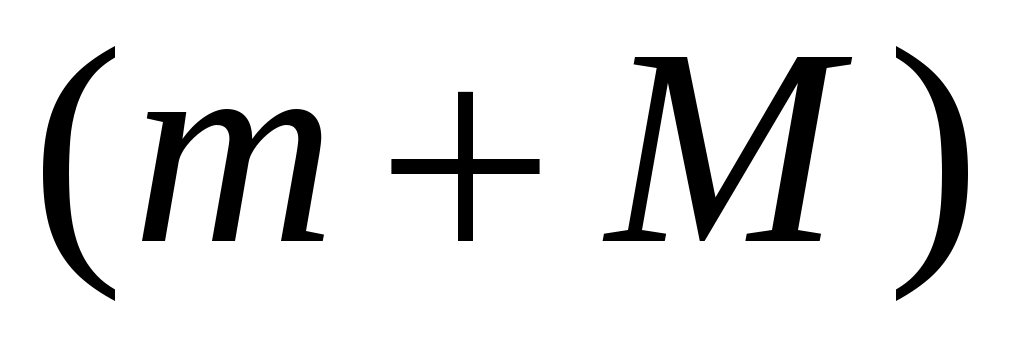 и очевидных преобразований имеем:
и очевидных преобразований имеем:
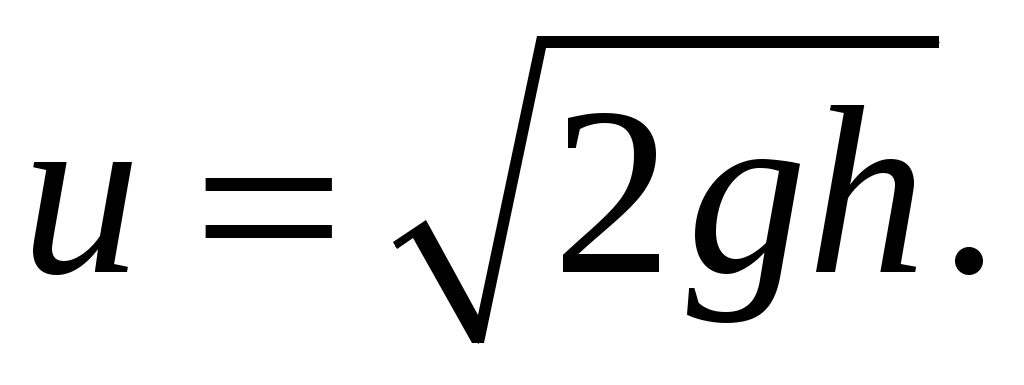 (1.4)
(1.4)
Таким образом, равенства (1.2) и (1.4) связывают между собой первое и третье состояние. Исключая из них скорость маятника u, получим:
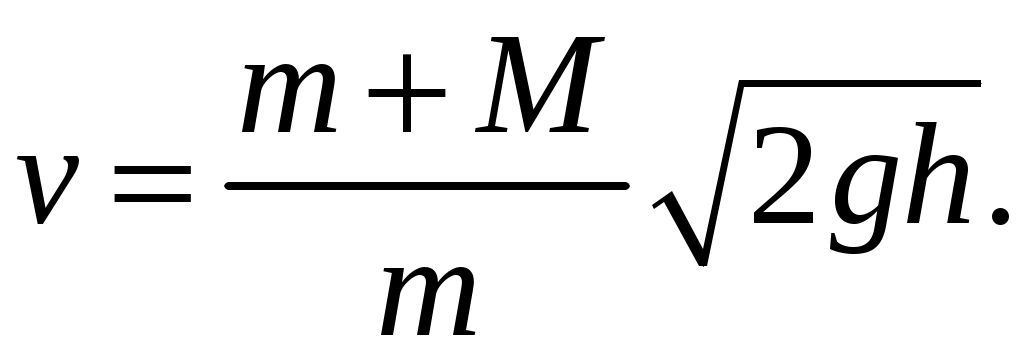 (1.5)
(1.5)
Высоту подъема h маятника измерить труднее, чем горизонтальное смещение S (см. рис. 1.2), поэтому выразим эту величину через S и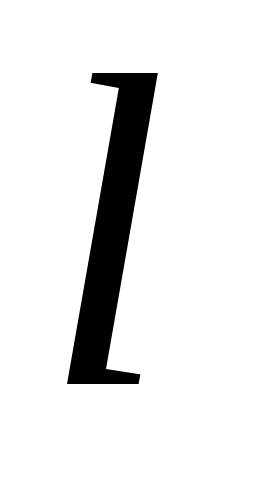 , которые можно легко измерить (
, которые можно легко измерить (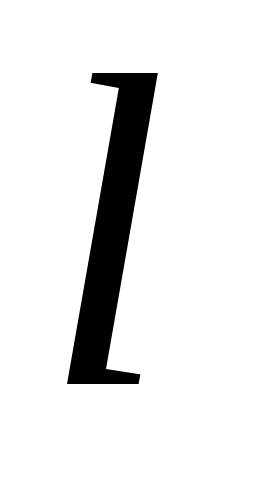 – длина подвеса маятника). Пусть φ – угол отклонения маятника от вертикали, тогда
– длина подвеса маятника). Пусть φ – угол отклонения маятника от вертикали, тогда
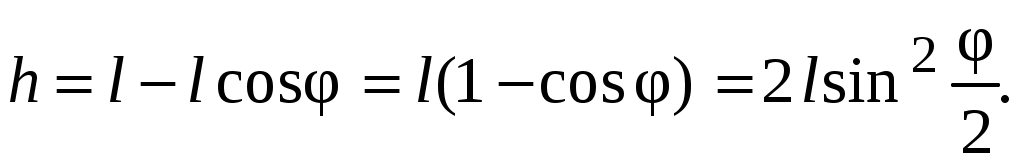
Если , то
, то 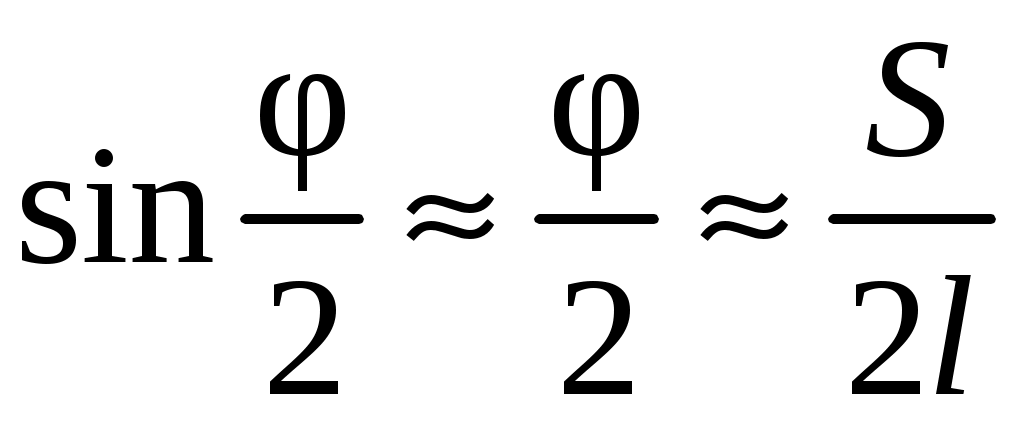 ,
,
тогда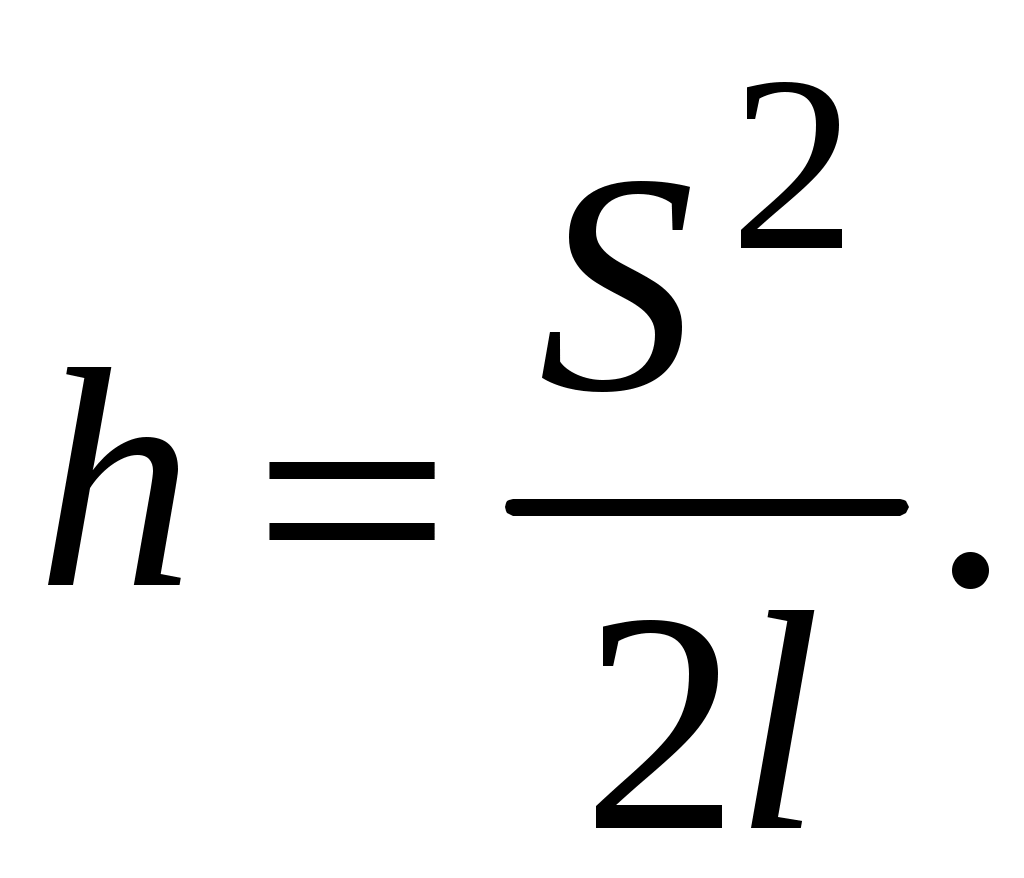
Следовательно, можно получить рабочую формулу для определения скорости пули:
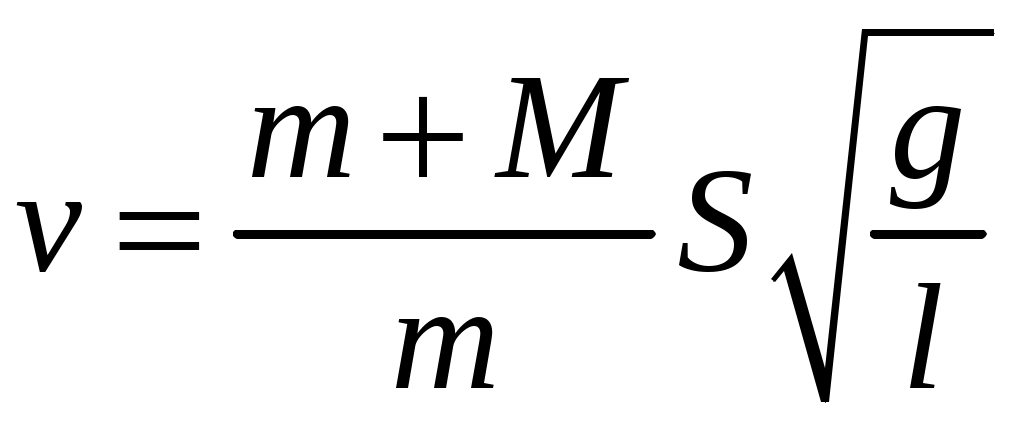 . (1.6)
. (1.6)
Здесь g = 9,81 м/с2 – ускорение свободного падения.
В процессе любого измерения за счет различных воздействий неизбежно появляются случайные ошибки.
Среднее значение скорости пули рассчитываем по формуле:
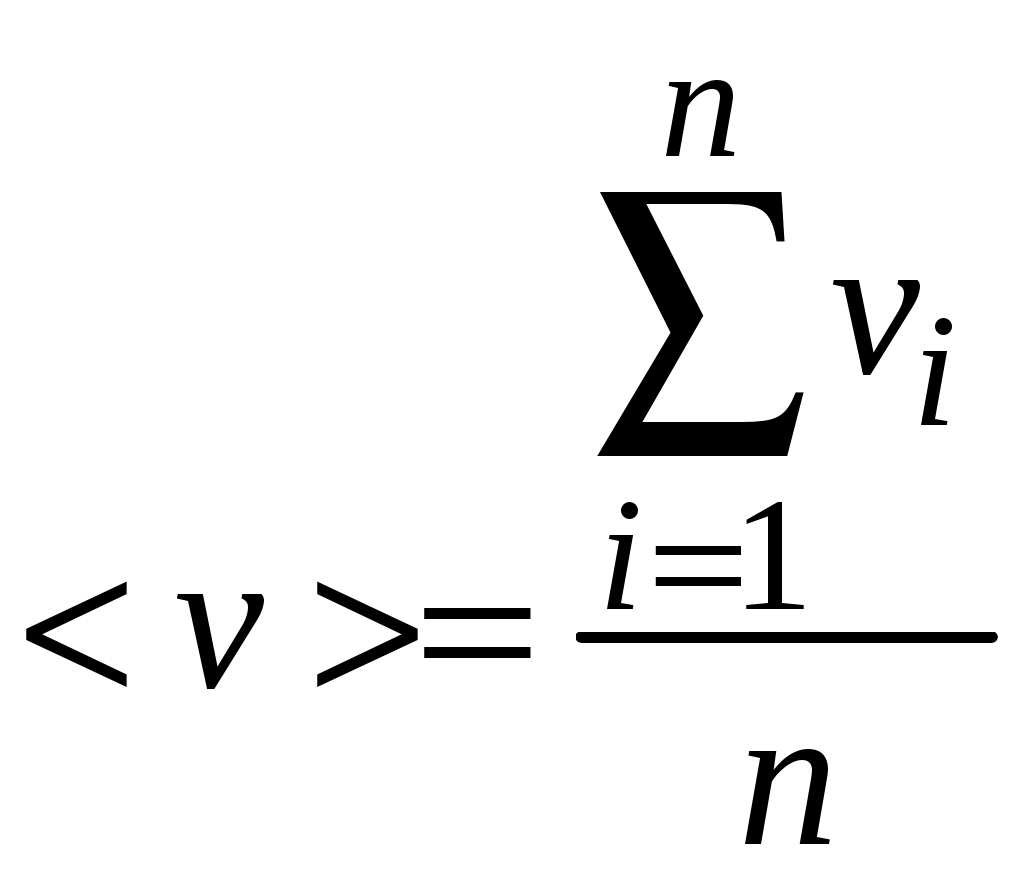 , (1.7)
, (1.7)
где n – число экспериментов, выполненных при одинаковых значениях начальных параметров;
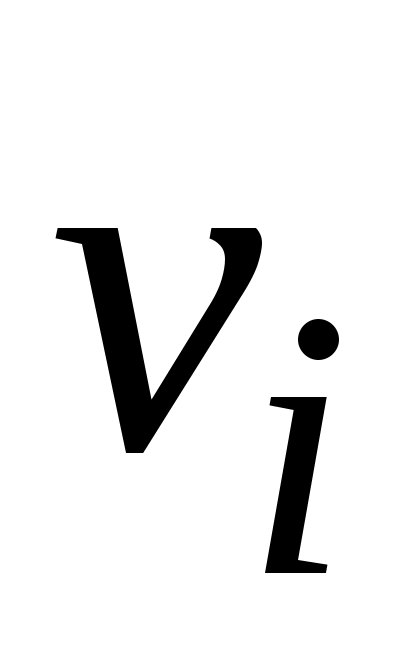 – значение скорости, рассчитанное для каждого такого эксперимента.
– значение скорости, рассчитанное для каждого такого эксперимента.
Среднеквадратичная погрешность для скорости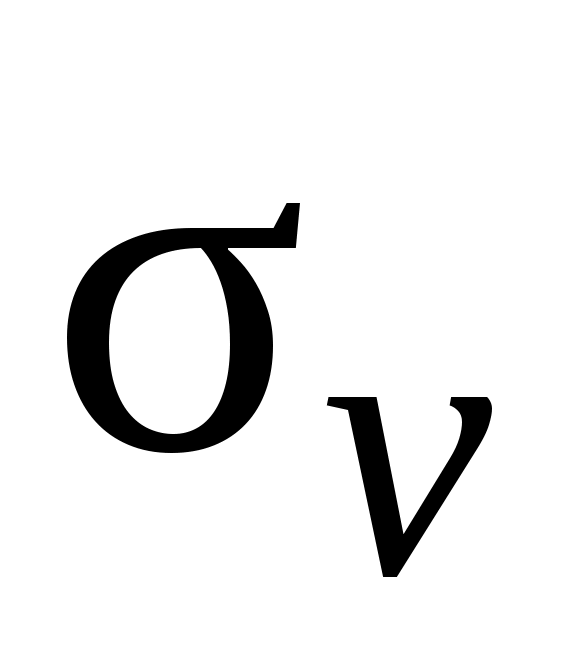 вычисляется по формуле:
вычисляется по формуле:
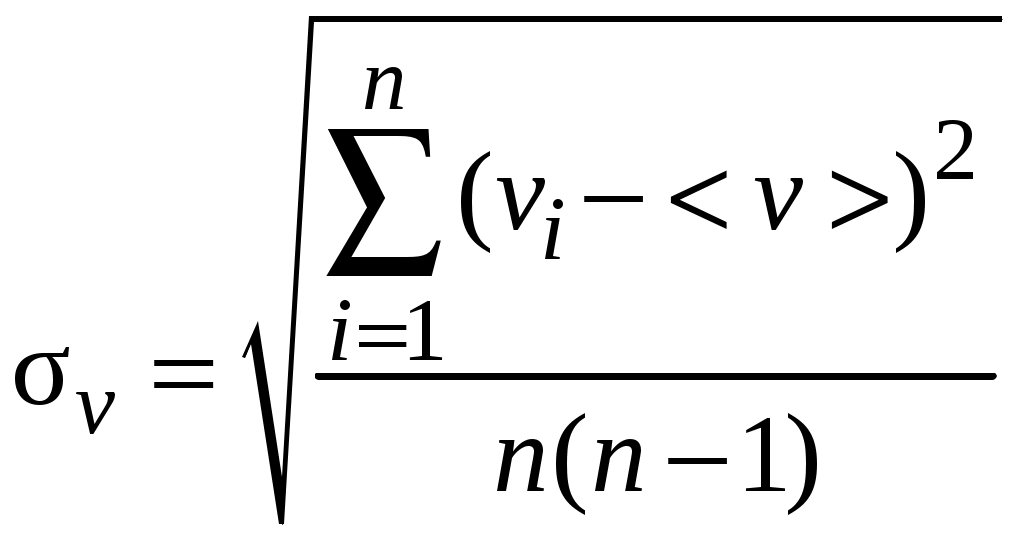 . (1.8)
. (1.8)
Порядок выполнения работы
Контрольные вопросы
Таблица 1.1
Список литературы
3. Савельев И. В. Курс общей физики. В 3 т. Т. 1. Механика. Молекулярная физика [Электронный ресурс] : учеб. пособие. – СПб. : Лань, 2016. – 436 с. – Режим доступа : http://e.lanbook.com/books/ element.php?pl1_id=71760.
2. Лабораторная работа № 2
Состояние 1 – пуля вылетела из пистолета, но еще не долетела до цилиндра. Цилиндр неподвижен.

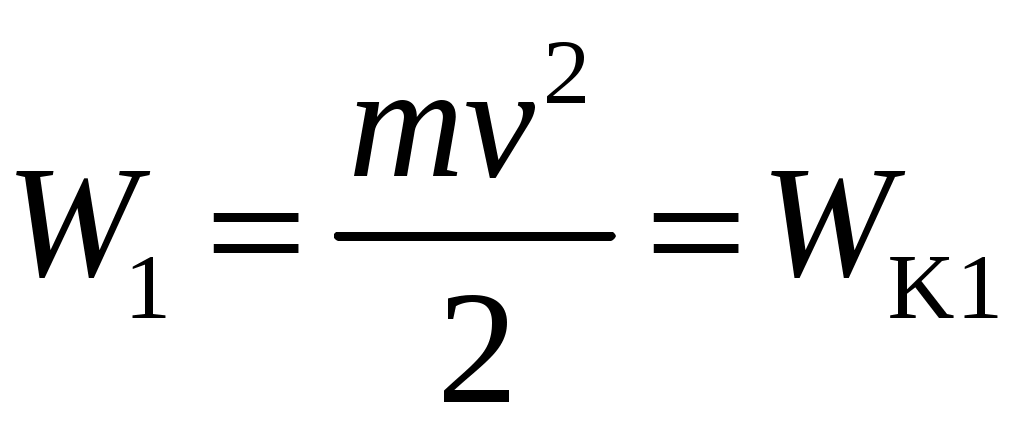
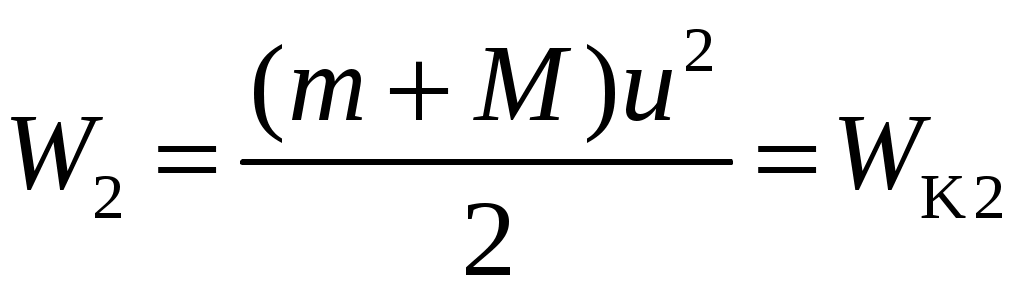
Рис. 1.2. Импульс и механическая энергия маятника в трех состояниях
Состояние 2 – пуля попала в цилиндр, цилиндр вместе с пулей начали движение со скоростью u, отклонение маятника приближенно равно нулю.
Состояние 3 – маятник отклонился на максимальный угол.
В процессе перехода системы из первого состояния во второе (процесс 1-2) сохраняется проекция полного импульса системы на горизонтальную ось, так как в момент удара горизонтальных внешних сил нет (сопротивлением воздуха пренебрегаем). Таким образом, горизонтальная проекция полного импульса системы до попадания пули в маятник
Таким образом, закон сохранения импульса связывает состояние 1 и состояние 2. Полная механическая энергия системы «пуля – маятник» в процессе 1-2 не сохраняется, так как при движении пули в пластилине действуют неконсервативные силы (силы трения и силы, возникающие при неупругой деформации пластилина).
Убыль механической энергии равна работе неконсервативных сил и, в конечном итоге, выделившемуся в системе теплу:
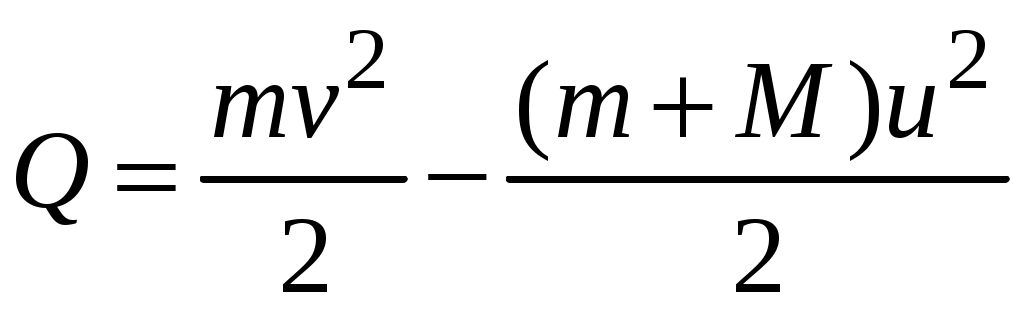
. (1.3)
В процессе 2-3 (перехода из второго состояние в третье) неконсервативные силы отсутствуют (сопротивлением воздуха и трением в подвесе можно пренебречь), поэтому к процессу 2-3 можно применить закон сохранения полной механической энергии:
где
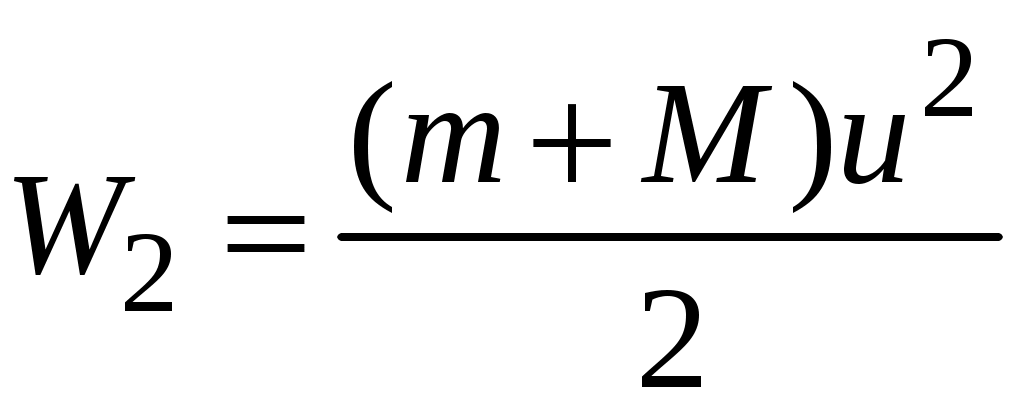 – полная механическая энергия системы «пуля – маятник» в состоянии 2;
– полная механическая энергия системы «пуля – маятник» в состоянии 2;Приравнивая
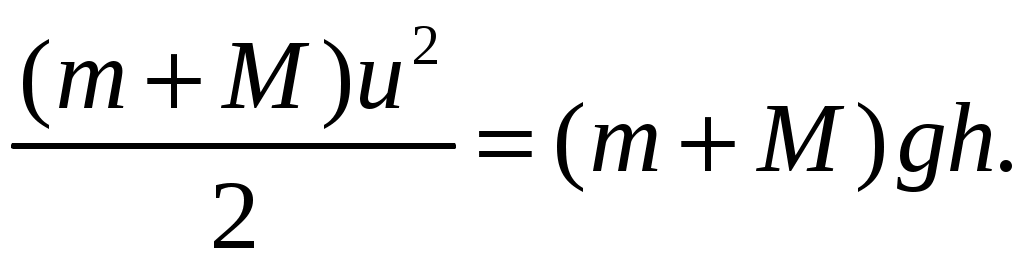
После сокращения на
Таким образом, равенства (1.2) и (1.4) связывают между собой первое и третье состояние. Исключая из них скорость маятника u, получим:
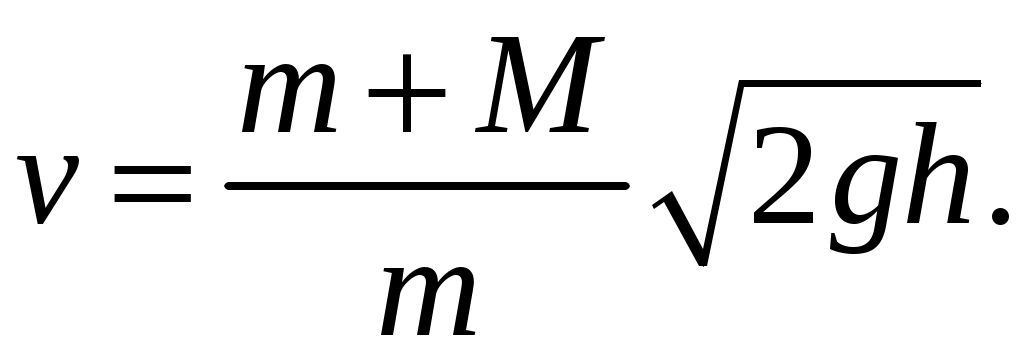 (1.5)
(1.5)Высоту подъема h маятника измерить труднее, чем горизонтальное смещение S (см. рис. 1.2), поэтому выразим эту величину через S и
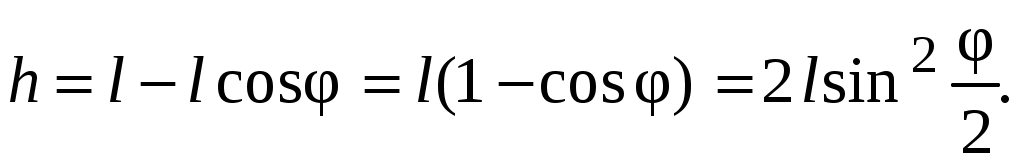
Если
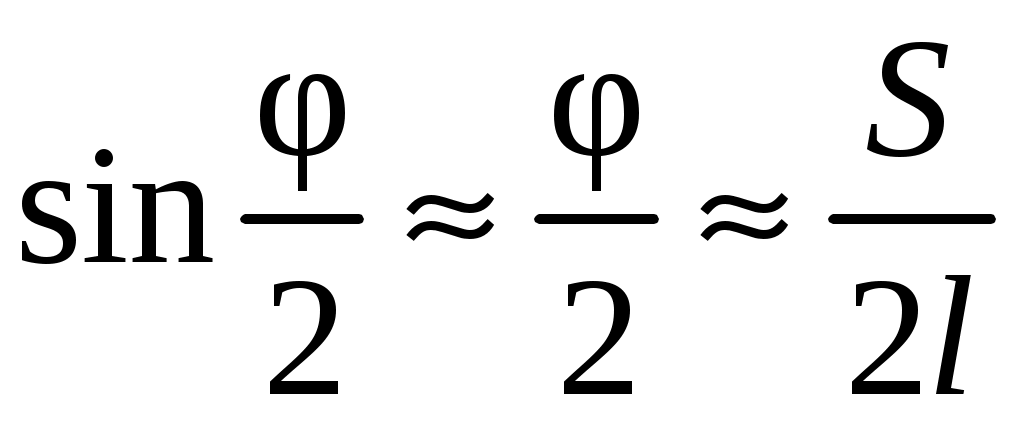 ,
, тогда
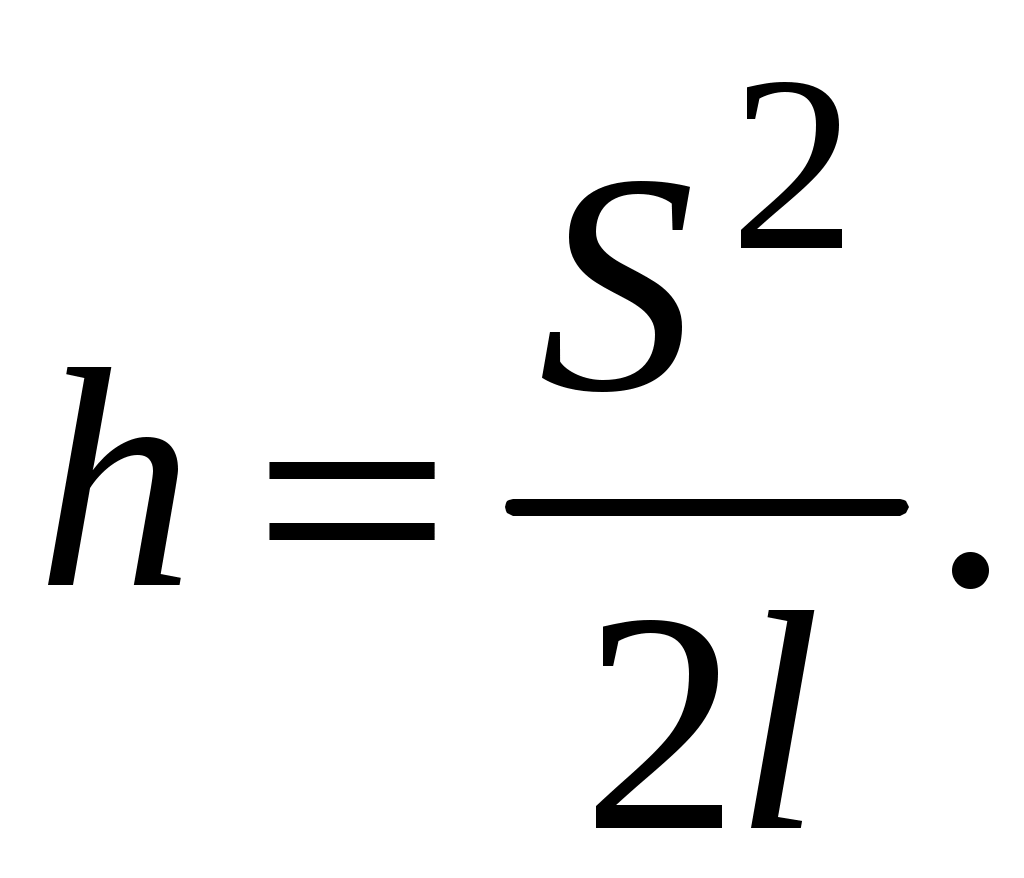
Следовательно, можно получить рабочую формулу для определения скорости пули:
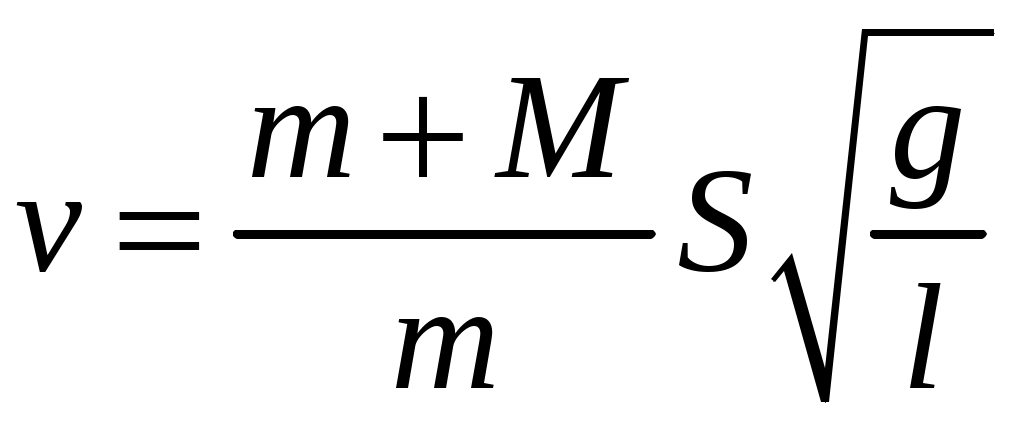 . (1.6)
. (1.6)Здесь g = 9,81 м/с2 – ускорение свободного падения.
В процессе любого измерения за счет различных воздействий неизбежно появляются случайные ошибки.
Среднее значение скорости пули рассчитываем по формуле:
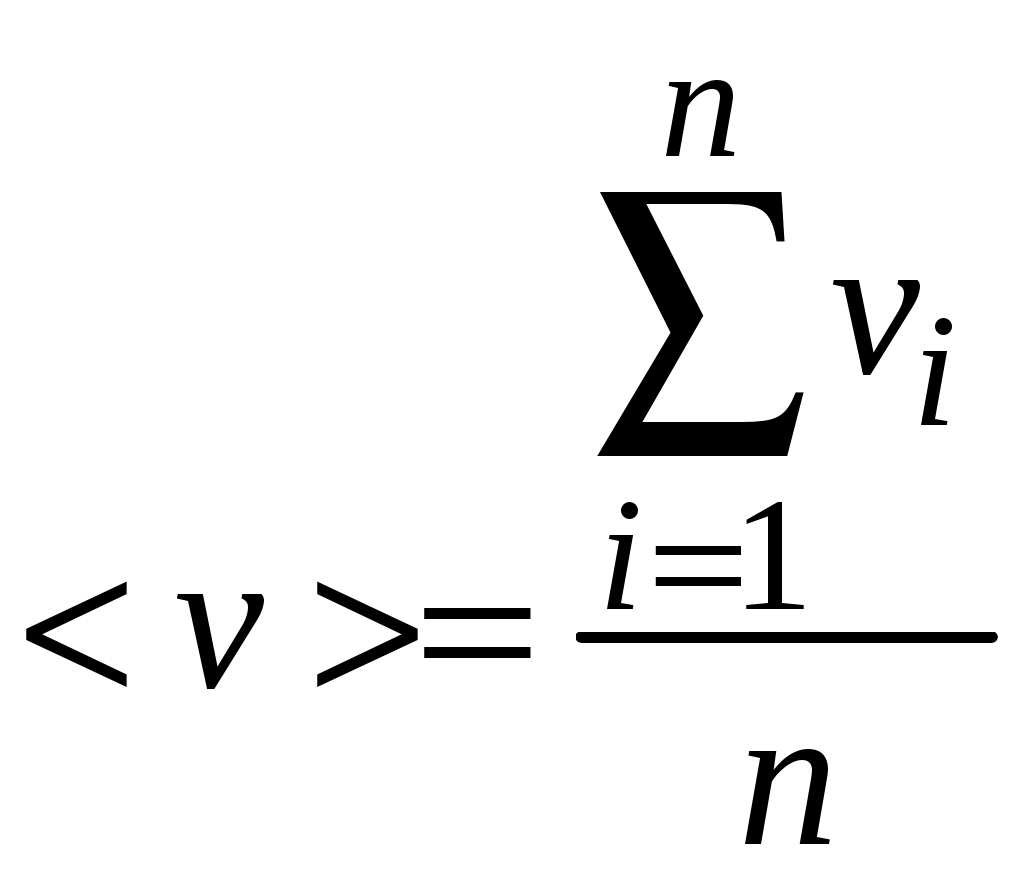 , (1.7)
, (1.7)где n – число экспериментов, выполненных при одинаковых значениях начальных параметров;
Среднеквадратичная погрешность для скорости
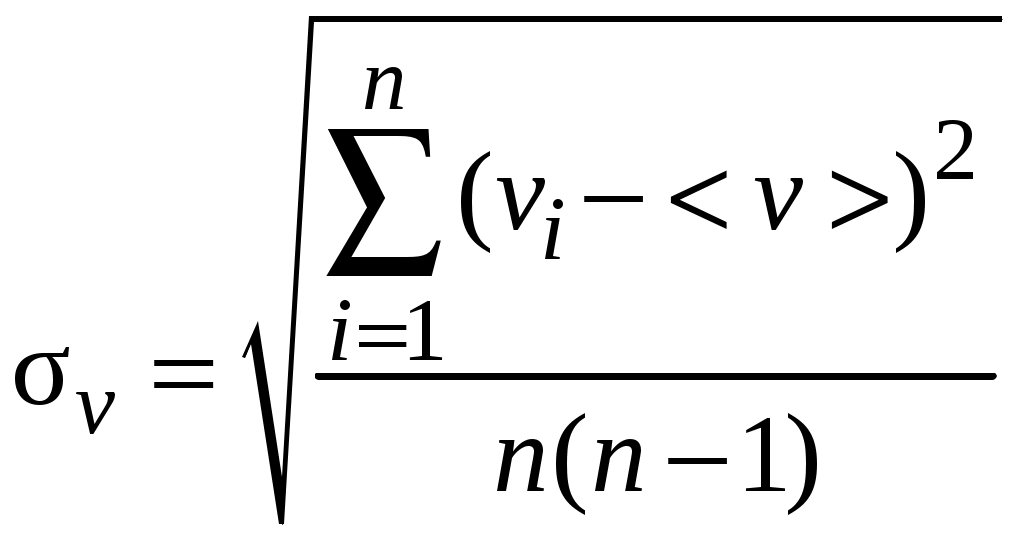 . (1.8)
. (1.8)Порядок выполнения работы
-
Измерьте длину подвеса маятника (расстояние по вертикали от центра цилиндра маятника до горизонтальной прямой, проходящей через точки, в которых крепится нить), значение массы маятника указано на цилиндре. -
Отметьте по шкале отсчетной линейки положение указателя x0 при неподвижном маятнике. -
Оттяните поршень пистолета до конца, тем самым его зафиксировав. Вставьте пулю в ствол пистолета до упора таким образом, чтобы острый ее конец был обращен к маятнику. -
Произведите выстрел из пистолета, для чего опустите курок вниз. Определите положение указателя x при максимальном отклонении маятника. Найдите смещение цилиндра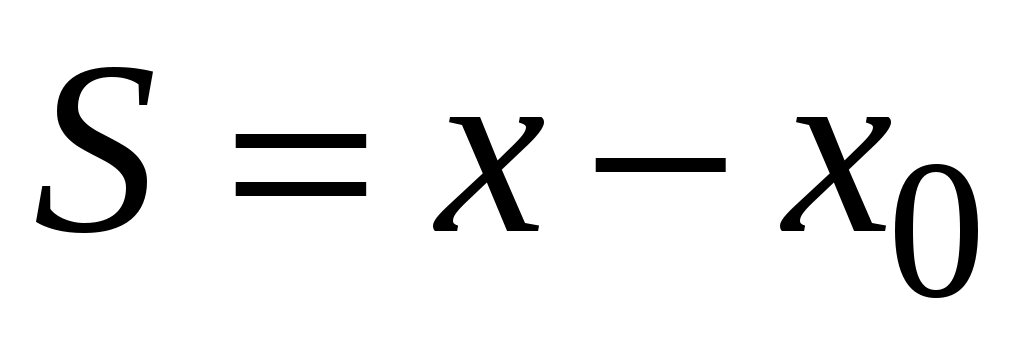 .
. -
Опыт произведите три раза. Перед повторными выстрелами систему необходимо привести в исходное положение (т. е. выстрел производить по неподвижно висящему маятнику). -
Повторите пункты 1–5 с пулями другой массы. -
Вычислите скорость пули по формуле (1.6). -
Результаты измерений и расчетов занесите в табл. 1.1. -
Вычислите погрешности измерений. -
Сформулируйте и запишите вывод по данной лабораторной работе.
Контрольные вопросы
-
Изобразите лабораторную установку в трех важных для вывода рабочей формулы состояниях. -
Под каждым рисунком напишите формулы для полного импульса и полной энергии системы «пуля – маятник» в соответствующем состоянии. -
Что называется полным импульсом системы? При каком условии полный импульс системы сохраняется? В каком из процессов нашей лабораторной работы полный импульс сохраняется? -
Что называется полной механической энергией системы? При каком условии полная механическая энергия системы сохраняется? В каком из процессов нашей лабораторной работы полная механическая энергия сохраняется? -
Используя ответы на предыдущие вопросы, выведите формулу, связывающую скорость пули с высотой поднятия маятника.
Таблица 1.1
| Масса маятника М = кг, длина подвеса l = м | |||||||||
| № пули | масса пули | № выстрела | x0, мм | x, мм | S, м | vi, м/с | <v>, м/с | Δv, м/с | σ, м/с |
| 1 | | 1 | | | | | | | |
| 2 | | | | | | ||||
| 3 | | | | | | ||||
| 2 | | 1 | | | | | | | |
| 2 | | | | | | ||||
| 3 | | | | | | ||||
| 3 | | 1 | | | | | | | |
| 2 | | | | | | ||||
| 3 | | | | | | ||||
Список литературы
-
Тюшев А. Н., Вылегжанина В. Д. Курс лекций по физике. Ч. 1. Механика : учеб. пособие. – Новосибирск : СГГА, 2011. – 144 с. -
Трофимова Т. И. Курс физики : учеб. пособие. – М. : Академия, 2015. – 560 с.
3. Савельев И. В. Курс общей физики. В 3 т. Т. 1. Механика. Молекулярная физика [Электронный ресурс] : учеб. пособие. – СПб. : Лань, 2016. – 436 с. – Режим доступа : http://e.lanbook.com/books/ element.php?pl1_id=71760.
2. Лабораторная работа № 2