ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 157
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определение момента инерции маятника обербека
Цель работы
Изучить зависимость момента инерции маятника Обербека от расположения масс на стержнях, используя закон сохранения энергии, и определить момент инерции маятника.
Приборы и принадлежности:
-
маятник Обербека; -
набор грузов; -
штангенциркуль; -
линейка; -
секундомер.
Подготовка к работе
По лекциям и приведенному ниже списку литературы изучите следующие вопросы:
-
кинематика вращательного движения (величины и их размерности); -
момент инерции твердого тела относительно оси вращения; -
кинетическая энергия вращающегося твердого тела; -
основное уравнение динамики вращательного движения; -
теорема Штейнера.
Вопросы для допуска к работе
-
Дайте определения угловой скорости и углового ускорения. -
Запишите основное уравнение динамики вращательного движения. -
Сформулируйте закон сохранения момента импульса. -
Сформулируйте определения следующих величин: момент импульса, момент инерции, момент силы. -
Сформулируйте теорему Штейнера.
Теоретическое введение
Понятия момента силы и момента импульса
Из опыта известно, что результат действия силы на тело, имеющее конечные размеры, зависит не только от величины и направления силы, но и от места (точки), к которому она приложена. Моментом силы
где
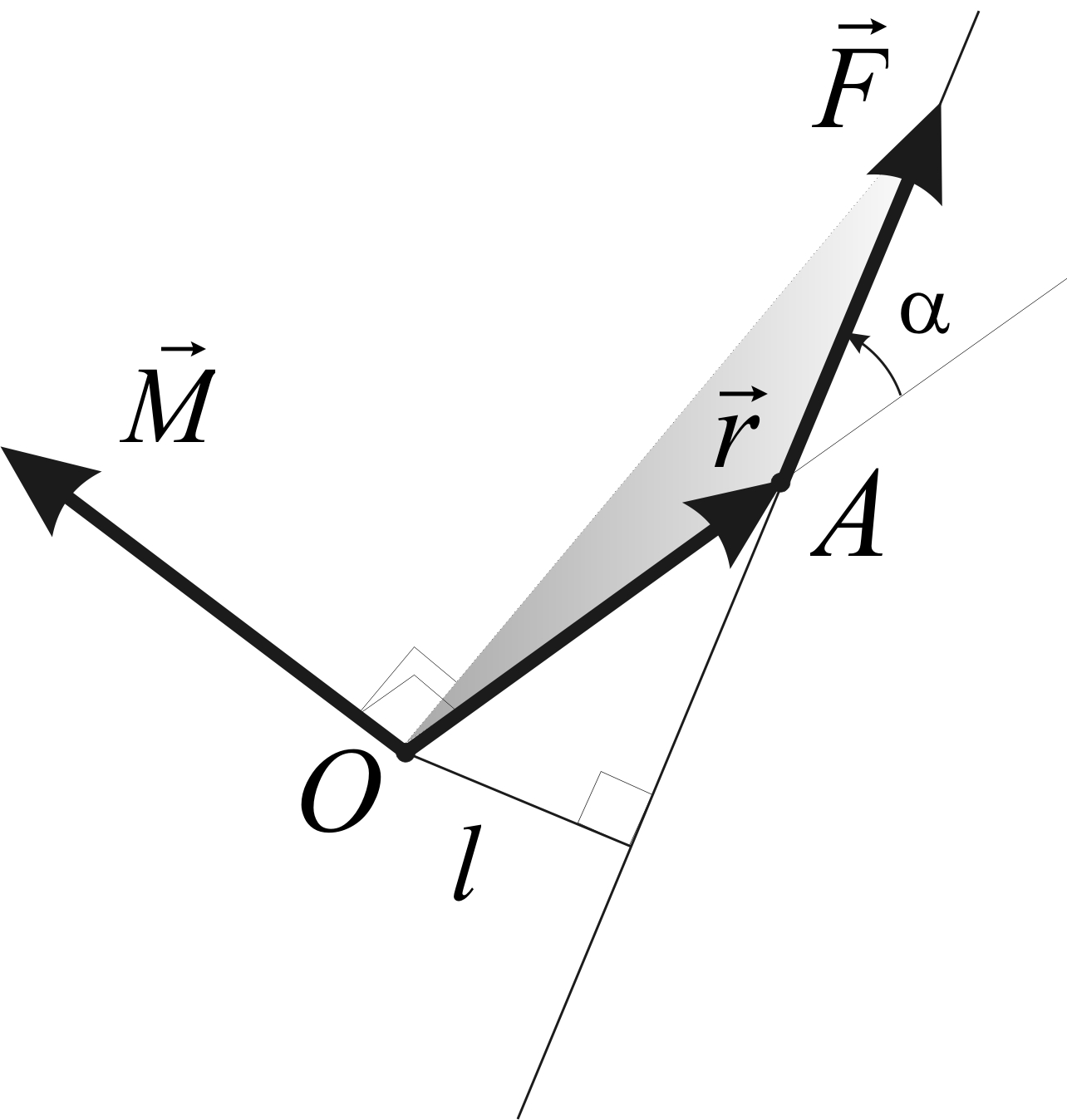
Рис. 2.1. Момент силы
относительно точки О
Как всякое векторное произведение, момент силы перпендикулярен обоим образующим его сомножителям, т. е. векторам
где α – угол между векторами
Из рис. 2.1 видно, что расстояние от точки О до прямой, вдоль которой действует сила
Это расстояние часто называют «плечом» силы
Заметим, что момент силы относительно точки равен нулю не только, если сила приложена прямо к этой точке (когда
Совершенно аналогично определяется момент импульса материальной точки относительно неподвижной точки О (рис. 2.2):
где
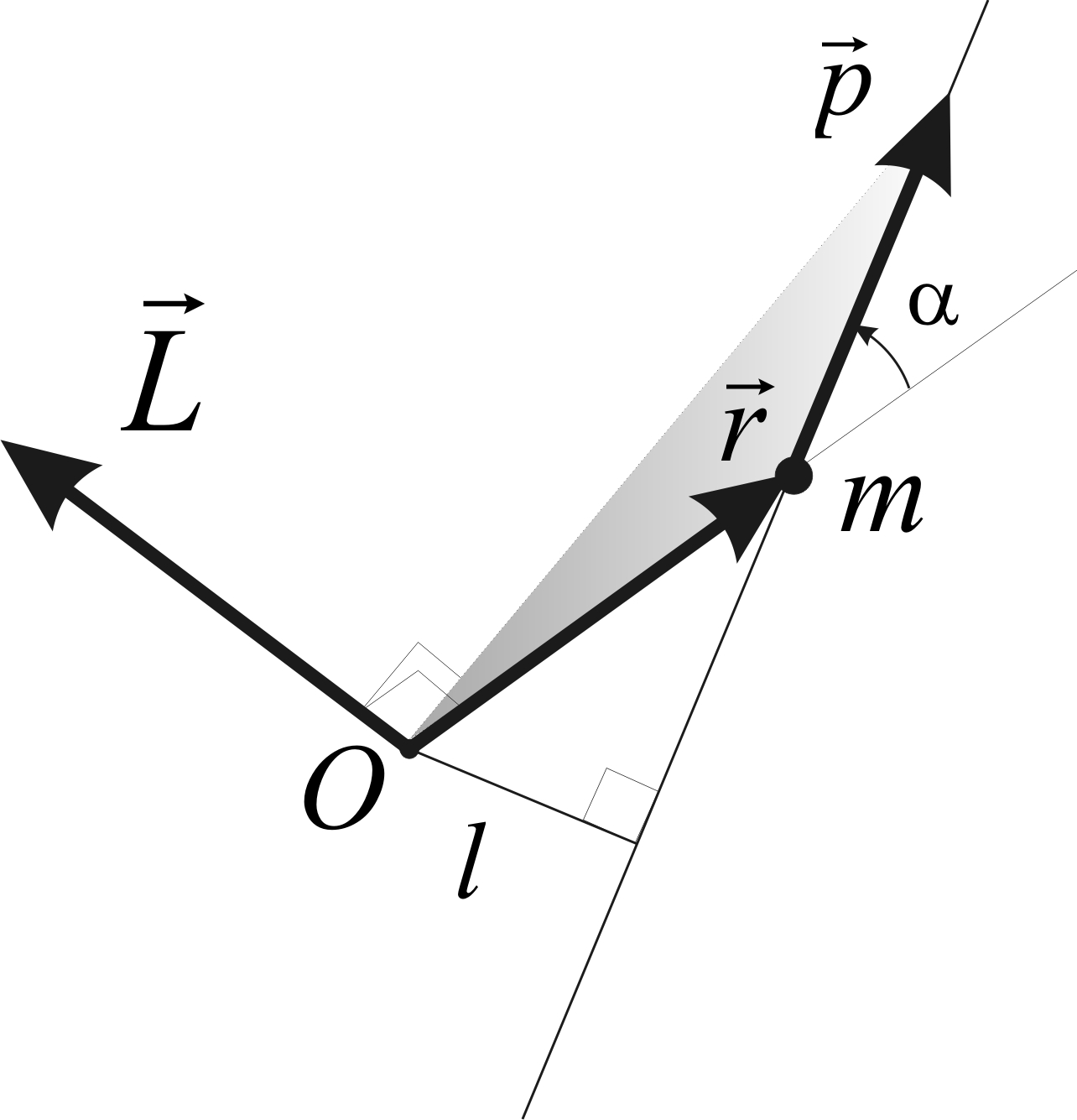
Рис. 2.2. Момент импульса материальной точки
m
относительно точки О
Если вспомнить определение импульса:
где m – масса точки;
получим:
Вектор момента импульса материальной точки перпендикулярен радиусу-вектору и вектору скорости точки, а значит и к плоскости, в которой они лежат, направлен по правилу правого винта («буравчика»). Его величина (модуль) определяется по формуле:
где α – угол между векторами
Основное уравнение динамики вращательного движения
Между моментом силы, действующим на тело, и моментом импульса тела существует фундаментальная связь. Дифференцируя момент импульса материальной точки по времени в соответствии с формулой производной произведения, получаем:
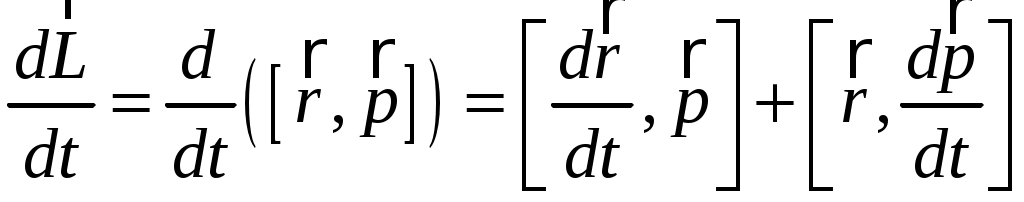 . (2.8)
. (2.8)Но, по определению скорости тела
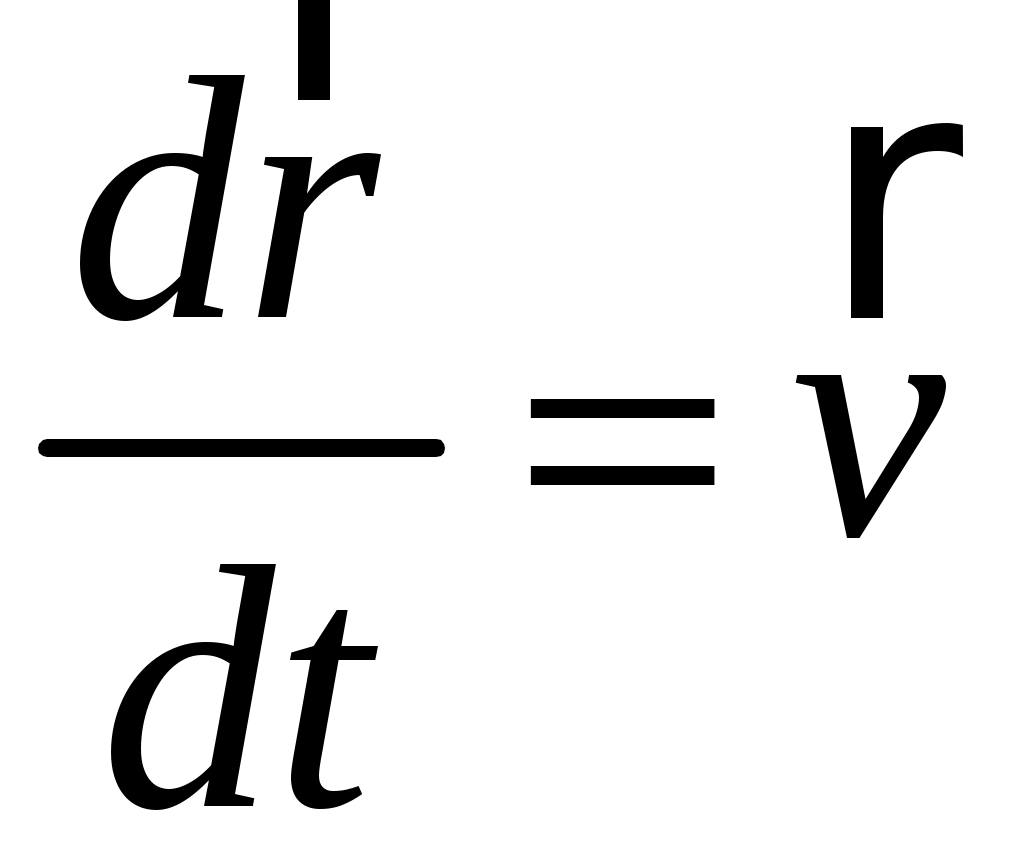 , (2.9)
, (2.9)а по II закону Ньютона
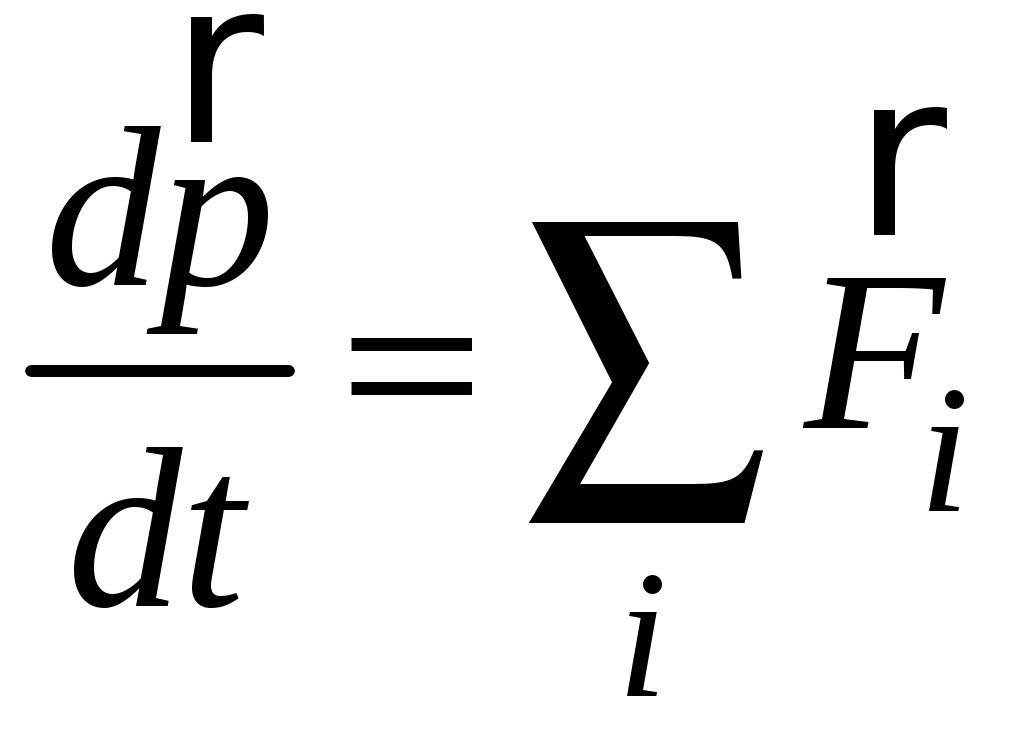 , (2.10)
, (2.10)где
Таким образом, имеем
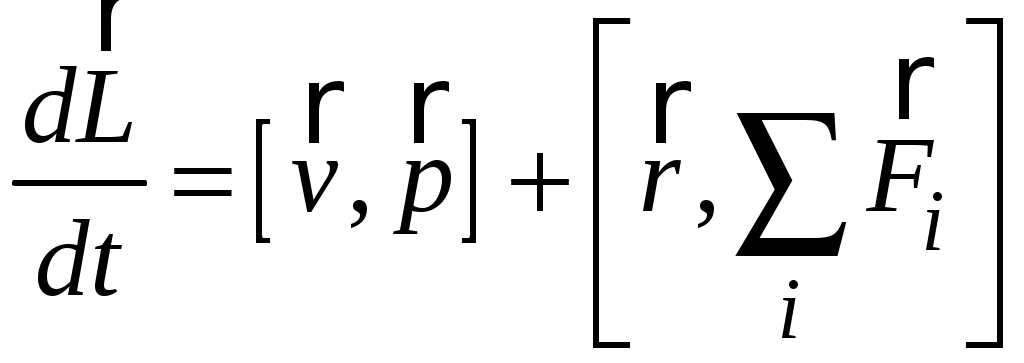 . (2.11)
. (2.11)Но векторы скорости и импульса точки всегда параллельны друг другу, поэтому всегда
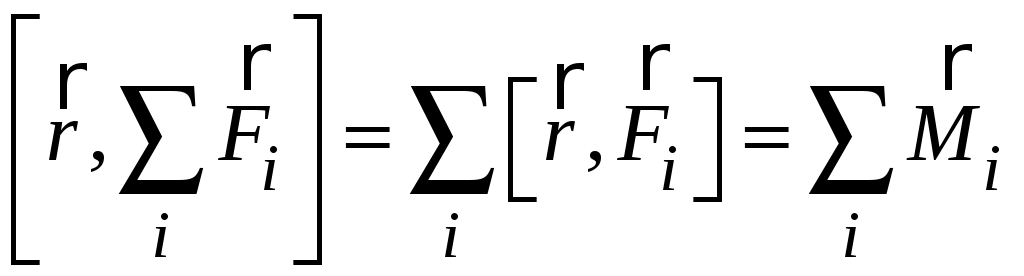 .
.Остается признать, что
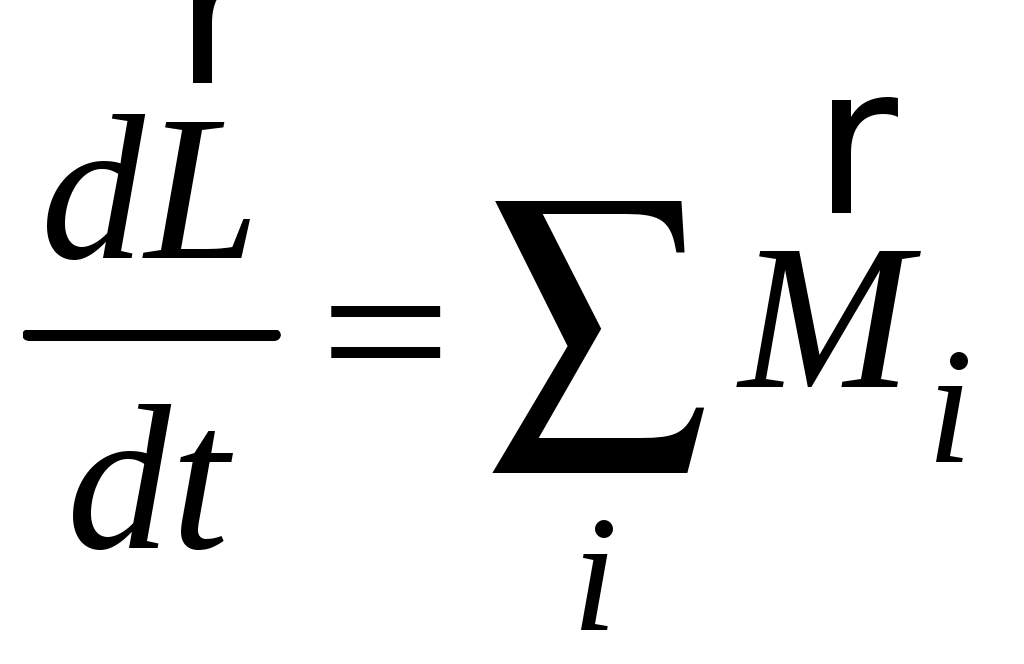
, (2.12)
то есть скорость изменения момента импульса точки равна результирующему моменту сил. Это и есть основное уравнение динамики вращательного движения. Сравните с II законом Ньютона (2.10)!
Закон сохранения момента импульса
Используя уравнение (2.12) и III закон Ньютона, можно получить закон сохранения момента импульса.
Рассмотрим систему из n материальных точек. Для каждой из точек можно записать свое уравнение (2.12). Мы получим систему из n таких уравнений. Если сложить левые и правые части этих уравнений, то получим уравнение, в левой части которого стоит сумма производных моментов импульса всех тел по времени, а в правой части – сумма всех моментов сил, действующих на все тела системы:
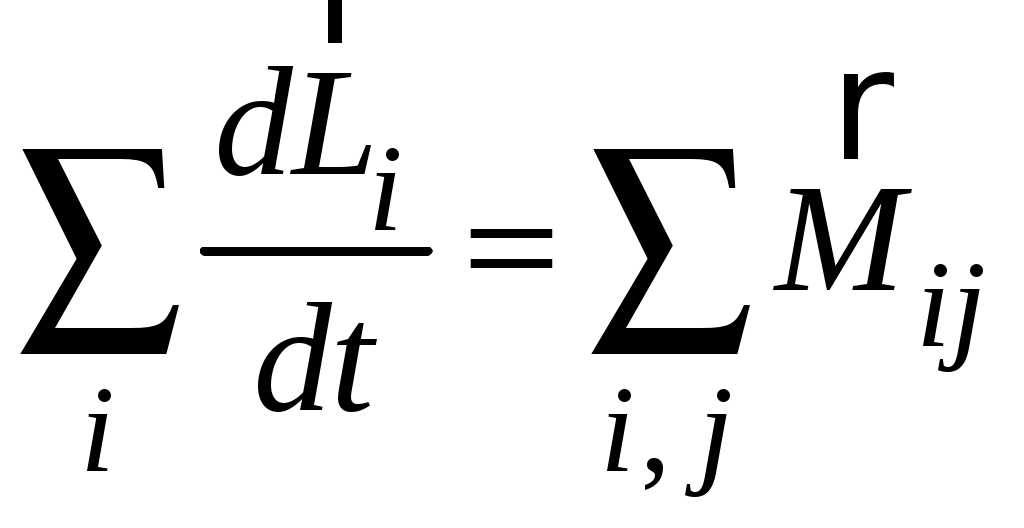 .
.Напоминаем, что среди сил различают внутренние и внешние. Из III закона Ньютона следует, что в любой системе равна нулю не только векторная сумма всех внутренних сил, но и векторная сумма их моментов. Это становится понятно, если вспомнить, что внутренние силы всегда возникают парами. Силы в такой паре не только одинаковы по величине и противоположны по направлению, но и действуют вдоль одной прямой, а значит, имеют одинаковое плечо. Это приводит к тому, что их моменты также будут одинаковы по величине, но противоположны по направлению и в сумме дадут нуль. Поэтому, как и в случае с законом сохранения импульса, нас интересуют только внешние силы:
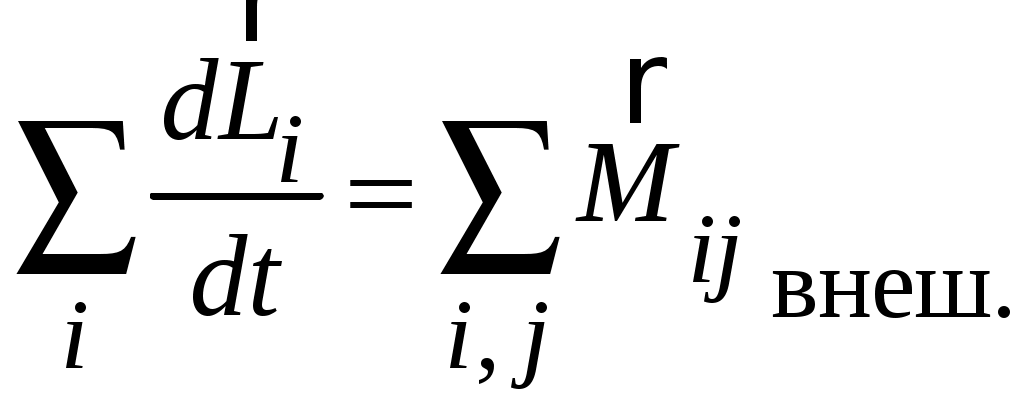
Если векторная сумма моментов внешних сил, стоящая в правой части этого равенства, равна нулю (так будет, если система замкнута, то есть внешние силы отсутствуют, либо действие моментов внешних сил взаимно компенсируется), то:
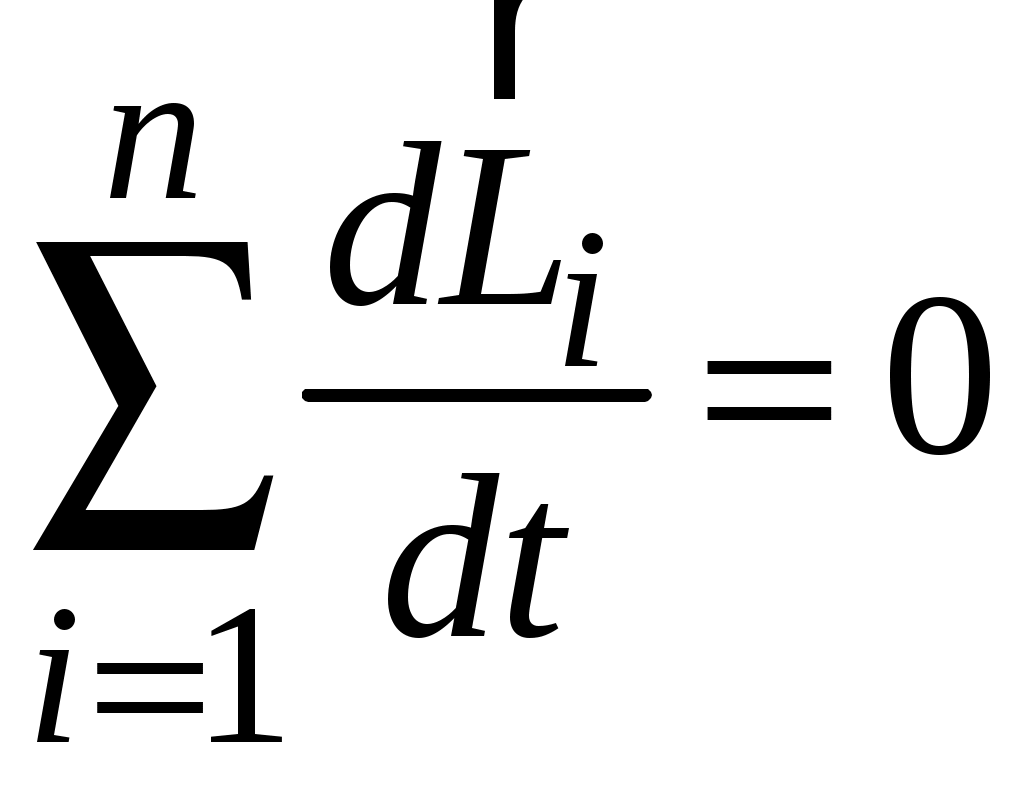 ,
,а поскольку сумма производных равна производной от суммы, то
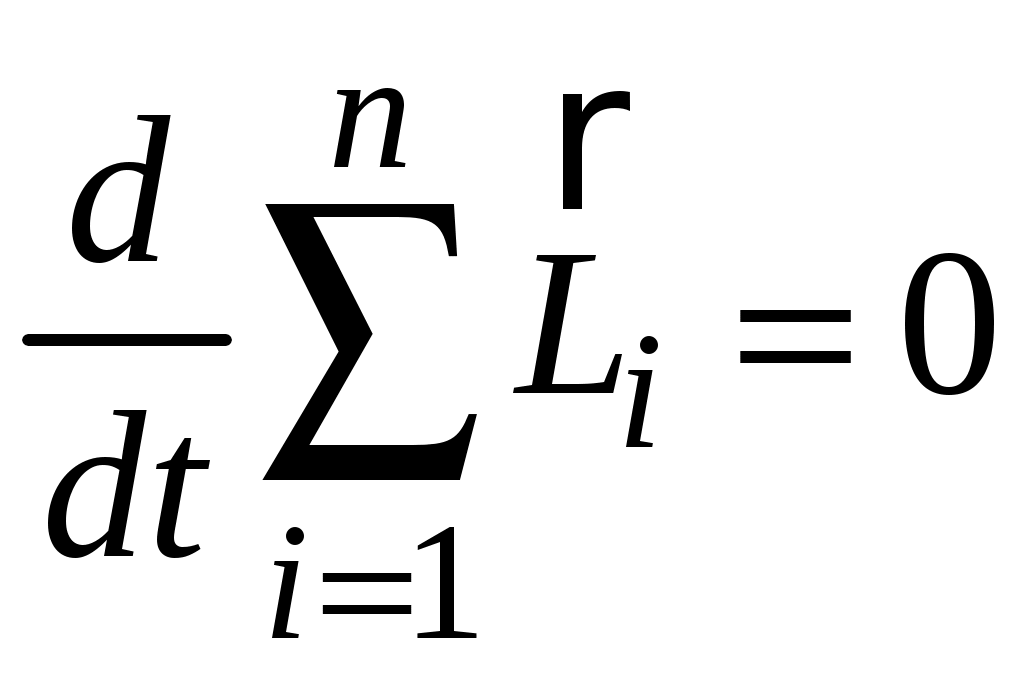 .
.Введем понятие момента импульса системы как векторную сумму моментов импульсов всех тел, входящих в эту систему:
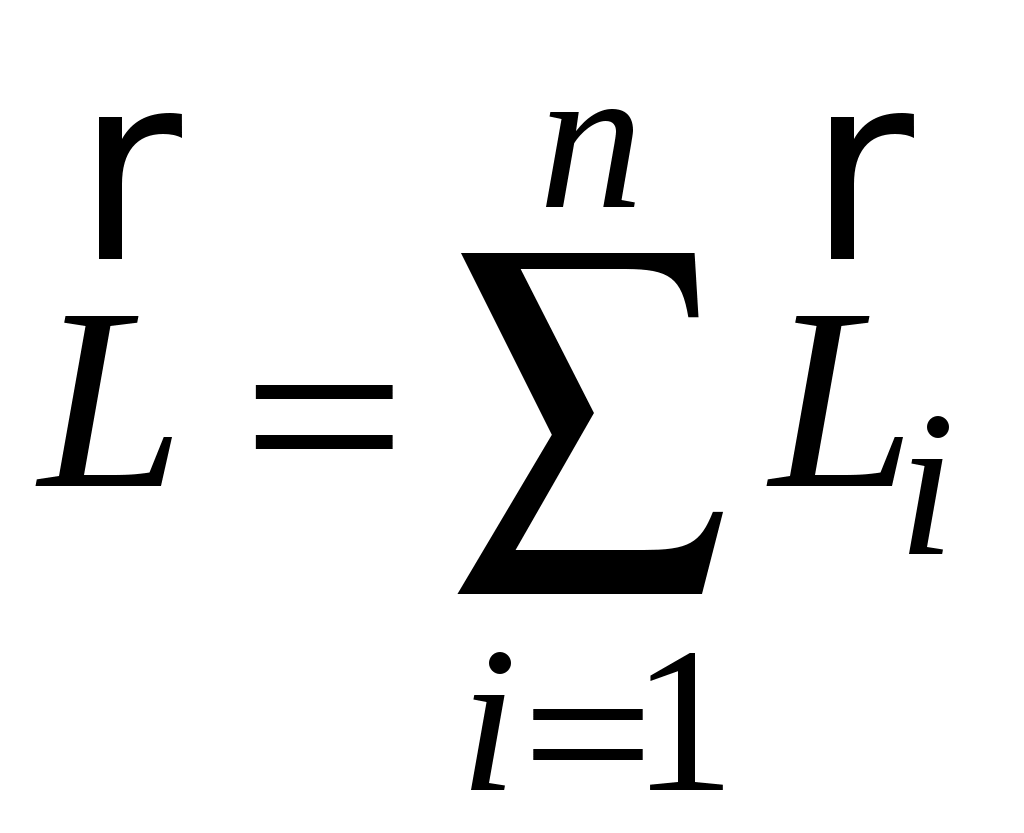 .
.Тогда производная по времени от момента импульса системы равна нулю, т. е.
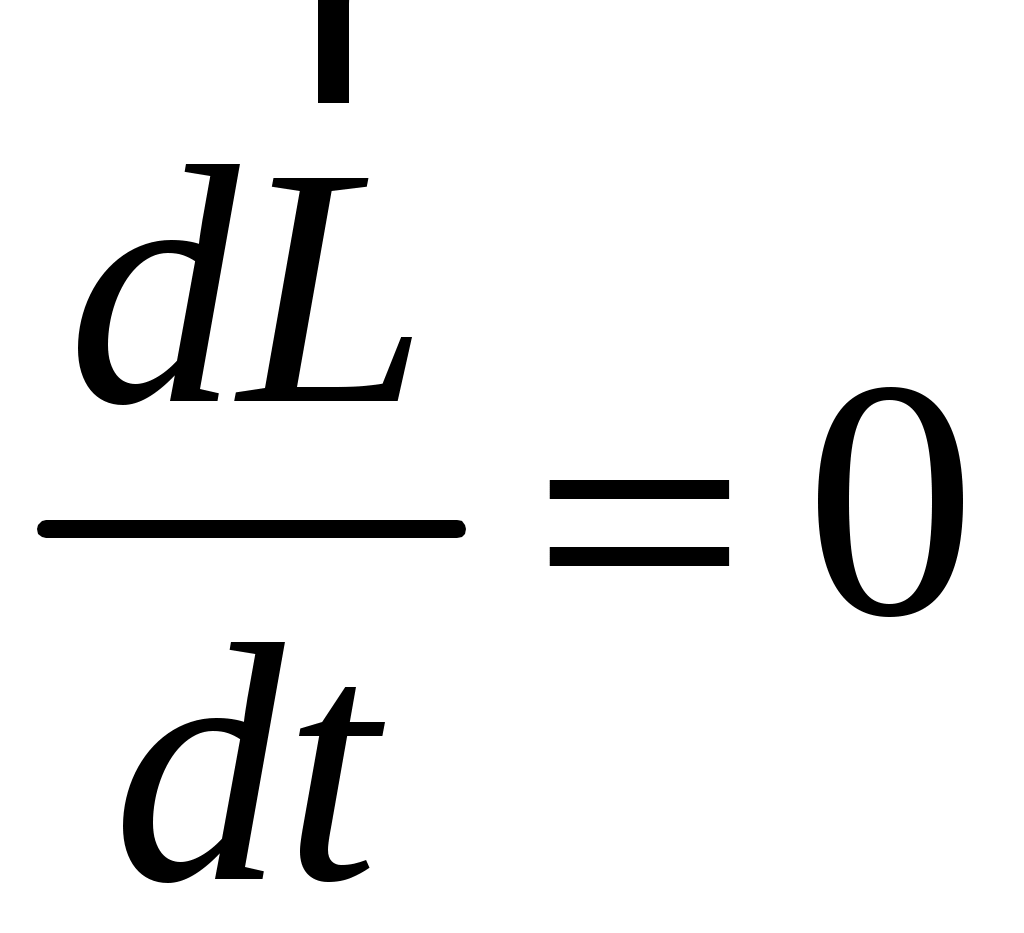 .
.Отсюда следует, что
Таким образом, закон сохранения момента импульса формулируется так: момент импульса системы остается постоянным тогда и только тогда, когда векторная сумма моментов внешних сил, действующих на систему, равна нулю.
Момент силы относительно оси и момент импульса
относительно оси
Уравнение (2.12) – векторное. Также как и (2.10), оно верно в проекциях на любую координатную ось, а значит, в нашем трехмерном пространстве оно равносильно системе из трех независимых скалярных уравнений:
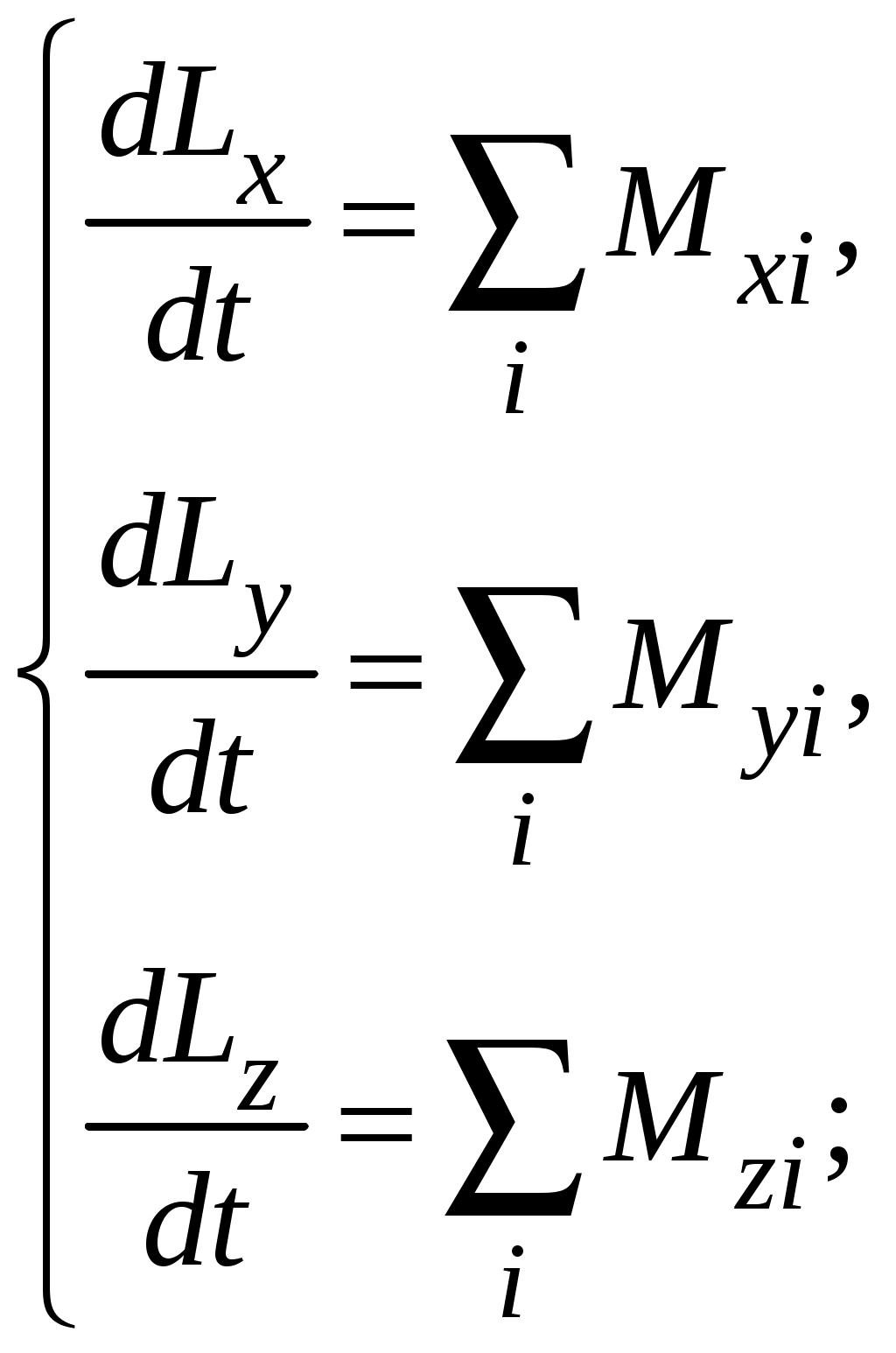 ,
,где Lx, Ly, Lz, – проекции вектора момента импульса тела на оси координат x, y и z соответственно;
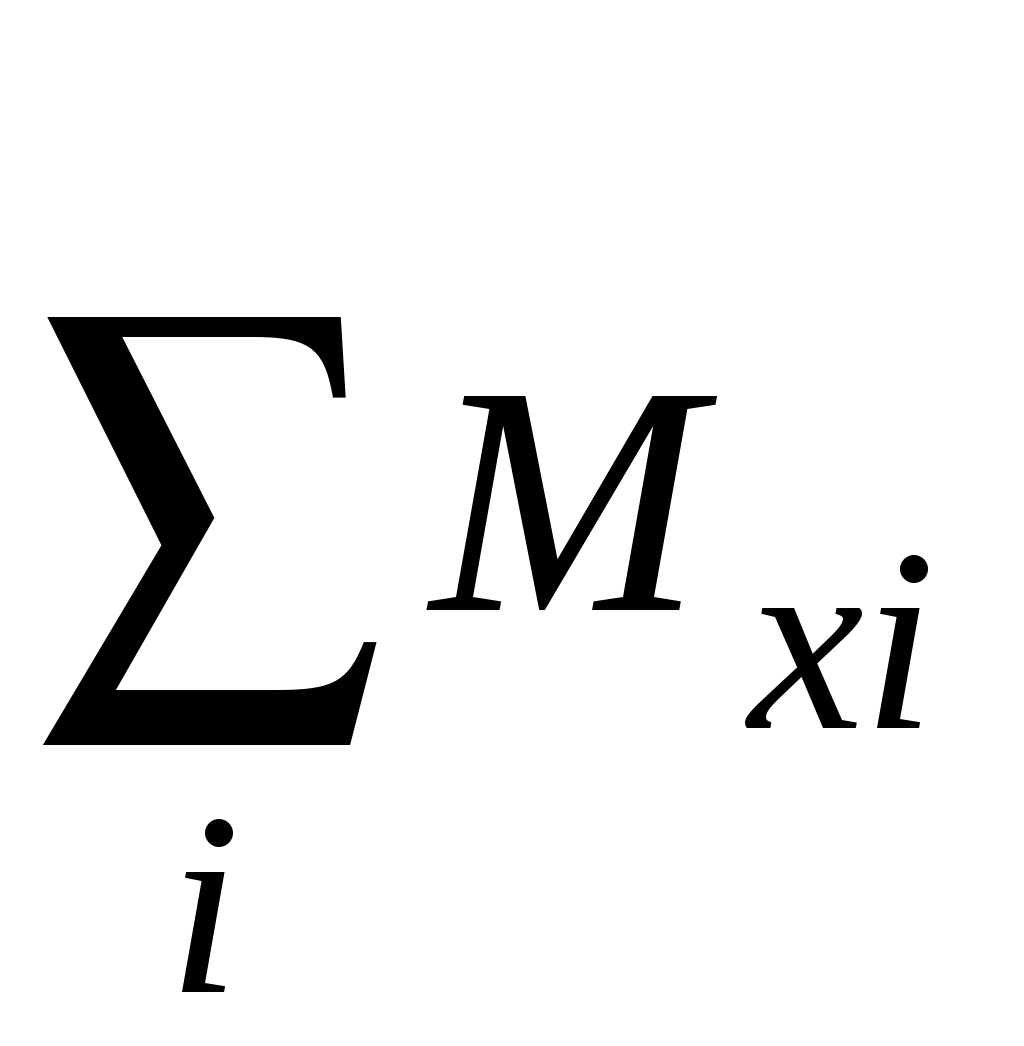 – алгебраическая сумма проекций моментов сил на ось x и т. п.
– алгебраическая сумма проекций моментов сил на ось x и т. п.Проекцию вектора момента силы на некоторую ось называют моментом силы относительно этой оси (например: Mz – «момент силы относительно оси z»).
Аналогично, проекцию вектора момента импульса тела на некоторую ось называют моментом импульса тела относительно этой оси (например: Lz – «момент импульса тела относительно оси z»).
Обратите внимание: момент относительно оси – это уже не вектор, а число, которое может быть как положительным, так и отрицательным.
Таким образом, скорость изменения момента импульса тела относительно некоторой оси равна алгебраической сумме моментов сил относительно данной оси.
Вращение твердого симметричного тела вокруг неподвижной оси
Тело, которое при движении не деформируется, т. е. сохраняет свою форму и размеры, называется абсолютно твердым телом. У такого тела расстояние между любыми двумя точками со временем не меняется.
Кинетическая энергия твердого тела, вращающегося вокруг оси z, вычисляется по формуле
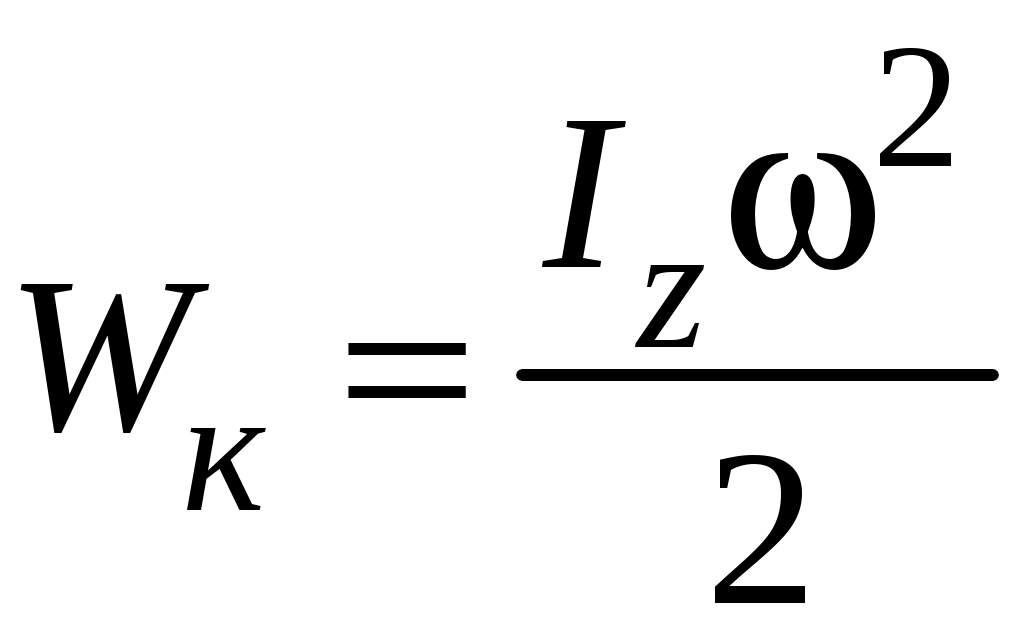 , (2.13)
, (2.13)где IZ – момент инерции