Файл: Механика. Электричество. Магнетизм.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 153

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ ПРИ ПОМОЩИ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Определение момента инерции маятника обербека

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ Цели работы: экспериментально исследовать квазистационарное электрическое поле, построить картину эквипотенциальных поверхностей и линий напряженности этого поля; определить значение модуля напряженности электрического поля в указанных точках. Приборы и принадлежности: электролитическая ванна; источник переменного напряжения; потенциометр с зондом. Подготовка к работеПо лекциям и приведенному ниже списку литературы изучите следующие вопросы: закон Кулона; понятие электрического поля; напряженность электрического поля, линии напряженности; потенциал электрического поля, эквипотенциальные линии; связь между напряженностью поля и потенциалом. Вопросы для допуска к работе Что называется напряженностью электрического поля? Что такое силовая линия электрического поля? Что называется потенциалом электростатического поля? Как расположены друг относительно друга в пространстве линии напряженности и эквипотенциальные поверхности? Как связаны между собой напряженность и потенциал в данной точке? Каковы условия равновесия зарядов на проводнике в электростатическом поле? Теоретическое введениеЭлектрическое поле возникает в пространстве при наличии заряженных тел. Неподвижные заряды создают поле, которое называется электростатическим. В природе существуют электрические заряды двух знаков: положительные «+» и отрицательные «–», это наименование условно. Наименьшим зарядом обладают элементарные частицы, например: электрон – частица, входящая в состав атома, – имеет отрицательный заряд –е (здесь е = 1,6 ∙ 10-19 Кл – «элементарный заряд»), а протоны входящие в состав ядра атома, заряжены положительно (+е). Заряды одинакового знака отталкиваются друг от друга, заряды противоположных знаков – притягиваются.По закону Кулона, силы взаимодействия двух точечных неподвижных зарядов q1 и q2 направлены вдоль прямой, их соединяющей, прямо пропорциональны величинам зарядов и обратно пропорциональны квадрату расстояния r12 между зарядами: (3.1)где – единичный вектор, направленный от одного заряда к другому, ε0 = 8,85 ∙ 10-12 Ф/м – электрическая постоянная,ε – диэлектрическая проницаемость среды.Эти силы являются центральными и, следовательно, консервативными.Отношение силы, действующей на пробный заряд, к величине этого заряда не зависит от величины заряда и называется напряженностью электрического поля . (3.2)Напряженность – векторная величина, ее направление совпадает с направлением силы , действующей на пробный положительный заряд , находящийся в данной точке пространства.Электростатическое поле можно представить графически с помощью системы линий напряженности (силовых линий), начинающихся на положительных зарядах и заканчивающихся на отрицательных или уходящих на бесконечность. Вектор напряженности в каждой точке силовой линии направлен по касательной к ней и совпадает с ней по направлению. Густота силовых линий пропорциональна модулю вектора напряженности .Сила, действующая на произвольный точечный заряд, помещенный в данную точку поля, определяется произведением величины этого заряда на напряженность электрического поля в данной точке . (3.3)Работа консервативных электростатических сил по перемещению заряда в электростатическом поле не зависит от траектории движения, а определяется лишь начальным и конечным положением заряда, эта работа может быть выражена через изменение потенциальной энергии заряда со знаком «–»: (3.4)Потенциальная энергия точечного заряда в электростатическом поле может быть выражена через энергетическую характеристику этого поля, называемую потенциалом φ, как произведение , следовательно, разность потенциалов между точками 1 и 2 можно определить через отношение работы сил поля к величине заряда (3.5)При бесконечно малом перемещении заряда под действием силы в произвольном направлении совершается элементарная работа . Тогда из (3.5), с учетом (3.3), получим, что для электростатического поля малая разность потенциалов связана с напряженностью выражением (3.6)где – проекция вектора на перемещение .Следовательно, . (3.7)В декартовой системе вектор напряженности электростатического поля может быть выражен через свои проекции Ex, Ey, Ez на оси соответственно: (3.8)где – орты координатных осей.Из математического определения частной производной функции многих переменных, применительно к функции и уравнения (3.7) следует (3.9)Это означает, что напряженность электростатического поля в любой точке может быть выражена через градиент потенциала в этой точке: (3.10)Напомним, что градиентом функции в векторной алгебре называется вектор, проекции которого на координатные оси равны частным производным от данной функции по соответствующим координатам. Градиент функции направлен в сторону ее наиболее быстрого возрастания, поэтому формула (3.10) показывает, что вектор напряженности направлен в сторону максимального убывания потенциала.Поверхности равного потенциала называются эквипотенциальными. Из соотношения (3.6) следует, что при перемещении заряда вдоль эквипотенциальной поверхности (d = 0) работа электростатического поля равна нулю, и это возможно только в том случае, когда вектор напряженности перпендикулярен этой поверхности (cos  = 0). Следовательно, силовые линии электростатического поля пересекают эквипотенциальные поверхности под прямым углом (рис. 3.1). Рис. 3.1. Взаимное расположение в пространстве силовых линий и эквипотенциальных поверхностей:1, 2 – проводники; 3 – эквипотенциальная поверхность;4 – линия напряженностиВнутри проводника всегда имеются свободные заряженные частицы, поэтому при внесении проводника во внешнее электростатическое поле свободные положительные заряды начинают двигаться в направлении вектора , а отрицательные – в противоположную сторону, на поверхности проводника образуются так называемые индуцированные заряды. Поле этих зарядов направлено противоположно внешнему полю. Перераспределение зарядов на проводнике будет происходить до тех пор, пока не будут выполнены следующие условия: (3.11)то есть: а) напряженность электрического поля внутри проводника равна 0; б) на поверхности проводника существует только нормальная составляющая электрического поля . Следовательно, поверхность проводника является эквипотенциальной и линии напряженности внешнего электрического поля перпендикулярны этой поверхности (см. рис. 3.1).Электрическое поле, напряженность которого одинакова во всех точках: называют однородным. Очевидно, что линии напряженности такого поля представляют собой параллельные прямые. Соответственно, эквипотенциальными поверхностями будут перпендикулярные к ним параллельные плоскости. Однородное поле возникает, например, между двумя параллельными плоскими заряженными проводниками, размеры которых велики по сравнению с расстоянием между ними (рис. 3.2). Напомним, что такая система проводников называется плоским конденсатором. Рис. 3.2. Однородное электрическое поле:1, 2 – параллельные проводники; 3 – эквипотенциальнаяповерхность; 4 – линия напряженностиВ однородном поле очень легко проинтегрировать уравнение (3.6), чтобы получить разность потенциалов между любыми двумя точками 1 и 2. Если учесть, что постоянный вектор напряженности можно вынести за знак интеграла, как любой постоянный множитель, то, интегрируя по произвольному пути L (см. рис. 3.2), получим: (3.12)где – вектор, проведенный от точки 1 к точке 2; – угол между векторами и .Если точки 1 и 2 лежат на одной линии напряженности, то есть векторы и параллельны, то угол  = 0 или 180°, и формула (3.12) превращается в . (3.13)Эта формула позволяет приближенно вычислить напряженность электрического поля в точке, в окрестности которой оно мало отличается от однородного. Достаточно провести через данную точку линию напряженности и измерить вдоль нее расстояние между ближайшими эквипотенциальными поверхностями с потенциалами 1 и 2, после чего найти величину напряженности по формуле (3.14)Экспериментальная установкаИзучение электростатического поля состоит в определении величины и направления вектора напряженности . Но на практике гораздо проще исследовать пространственное распределение потенциалов , построить картину эквипотенциальных поверхностей, и, используя взаимную перпендикулярность линий напряженности и эквипотенциальных поверхностей, воссоздать картину силовых линий электростатического поля.В данной лабораторной работе (рис. 3.3) исследуется квазистационарное электрическое поле, которое возникает в слабопроводящей среде (водопроводная вода), в которую помещены электроды – металлические проводники, подсоединенные к источнику переменного напряжения. Так как проводимость такой среды намного меньше проводимости проводника, то поверхность проводника с большой степенью точности можно считать эквипотенциальной, при этом топография поля в пространстве между электродами будет аналогична топографии электростатического поля заряженных проводников в непроводящей среде. Известно, что водопроводная вода содержит в небольших количествах молекулы солей металлов, которые в электрическом поле распадаются на ионы металлов и ионы оснований, и, в дальнейшем, могут выделяться в виде осадка вблизи электродов. Для исключения такого электролиза используется переменное напряжение U

Проверка справедливости закона ома. определение удельного сопротивления провоЛОКИ

ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ МАГНИТНОГО ПОЛЯ ЗЕМЛИ



1. Лабораторная работа № 1

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ ПРИ ПОМОЩИ БАЛЛИСТИЧЕСКОГО МАЯТНИКА


Цель работы

Определить скорость пули, используя законы сохранения импульса и механической энергии.

Приборы и принадлежности:

  1. баллистический маятник;

  2. пружинный пистолет;

  3. отсчетная шкала;

  4. набор пуль;

  5. линейка.

Подготовка к работе

По лекциям и приведенному ниже списку литературы изучите следующие вопросы:

  1. законы Ньютона;

  2. понятие импульса системы, закон сохранения импульса;

  3. консервативные и неконсервативные силы;

  4. понятие энергии, закон сохранения механической энергии.

Вопросы для допуска к работе

  1. Дайте определение импульса тела, импульса системы тел.

  2. Запишите основной закон динамики поступательного движения.

  3. Какие силы называются внешними, а какие – внутренними?

  4. Какая система называется замкнутой?

  5. Какие силы называются консервативными, какие – неконсервативными?

  6. Сформулируйте закон сохранения импульса для одного тела и для системы тел.

  7. Дайте понятия потенциальной энергии, кинетической энергии и полной механической энергии.

  8. При каких условиях сохраняется полная механическая энергия системы?

Теоретическое введение

Законы Ньютона

В основе классической динамики лежат три закона Ньютона.

Законы Ньютона справедливы только для инерциальных систем отсчета.

Инерциальная система отсчета – это система отсчета, в которой тела, не подверженные воздействию других тел, движутся прямолинейно и равномерно или покоятся.

I закон Ньютона

Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

II закон Ньютона

Второй закон Ньютона называют основным законом динамики поступательного движения. Он формулируется так: скорость изменения импульса тела равна действующей на тело результирующей силе:


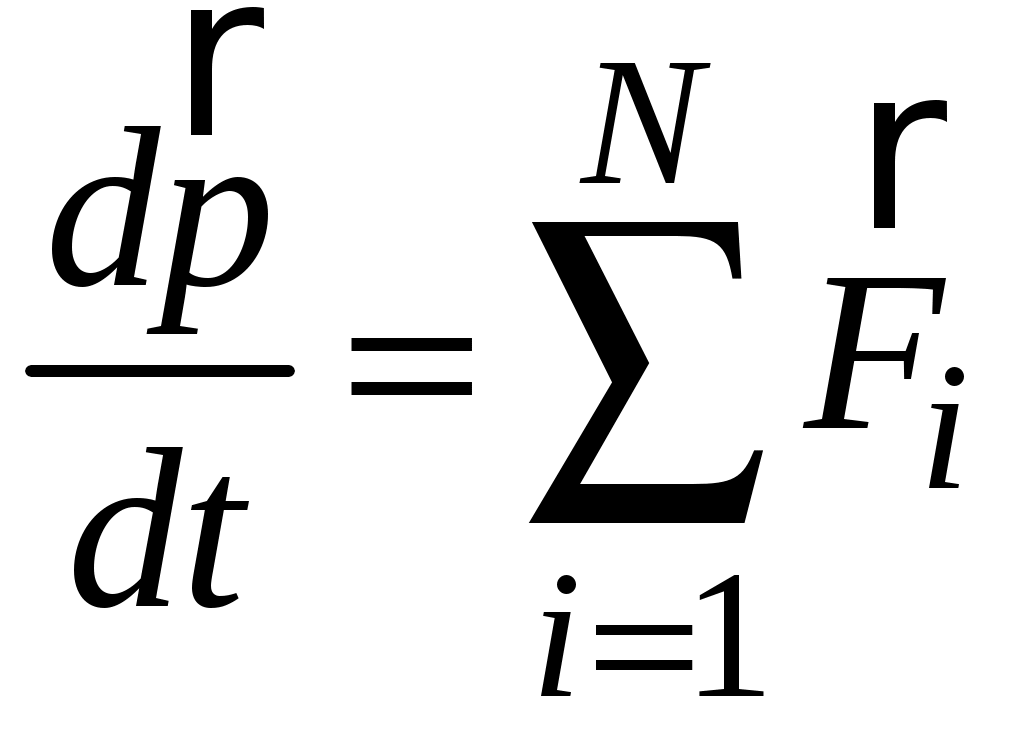. (1.1)

Сила 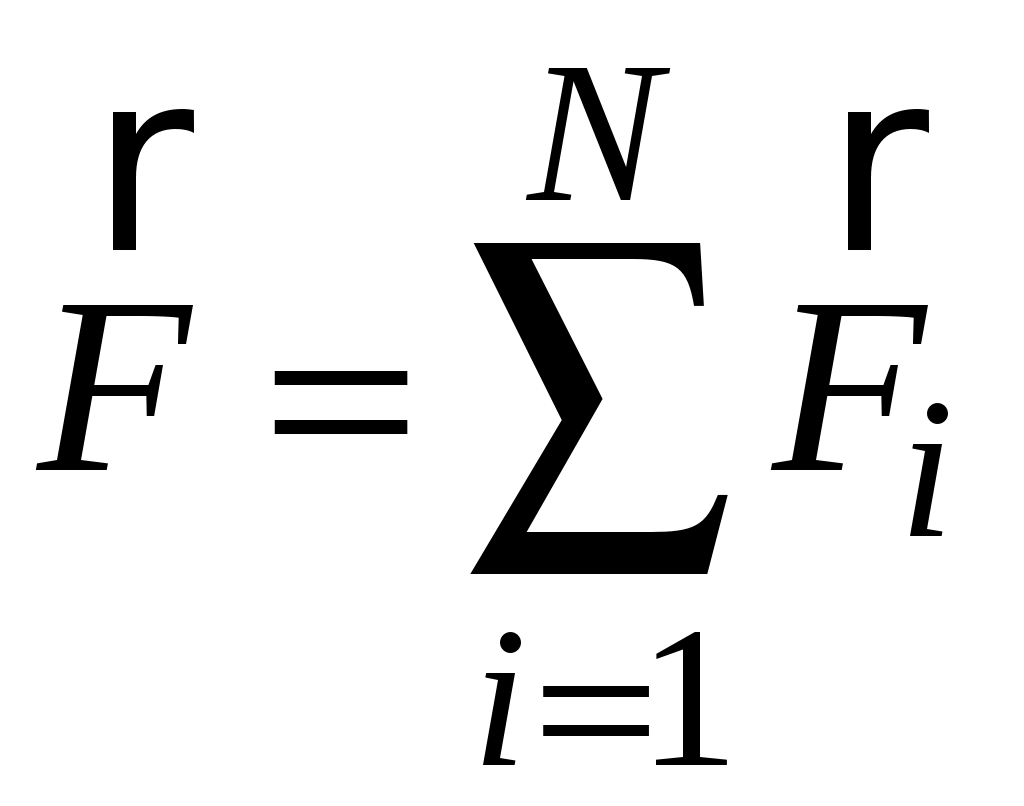– векторная сумма всех сил, действующих на данное тело со стороны других тел.

– импульс тела.

В частном случае, при , второй закон Ньютона может быть записан в следующем виде:

,

где – ускорение тела.

III закон Ньютона

Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению.

Подчеркнем, что эти силы приложены к разным телам (рис. 1.1).


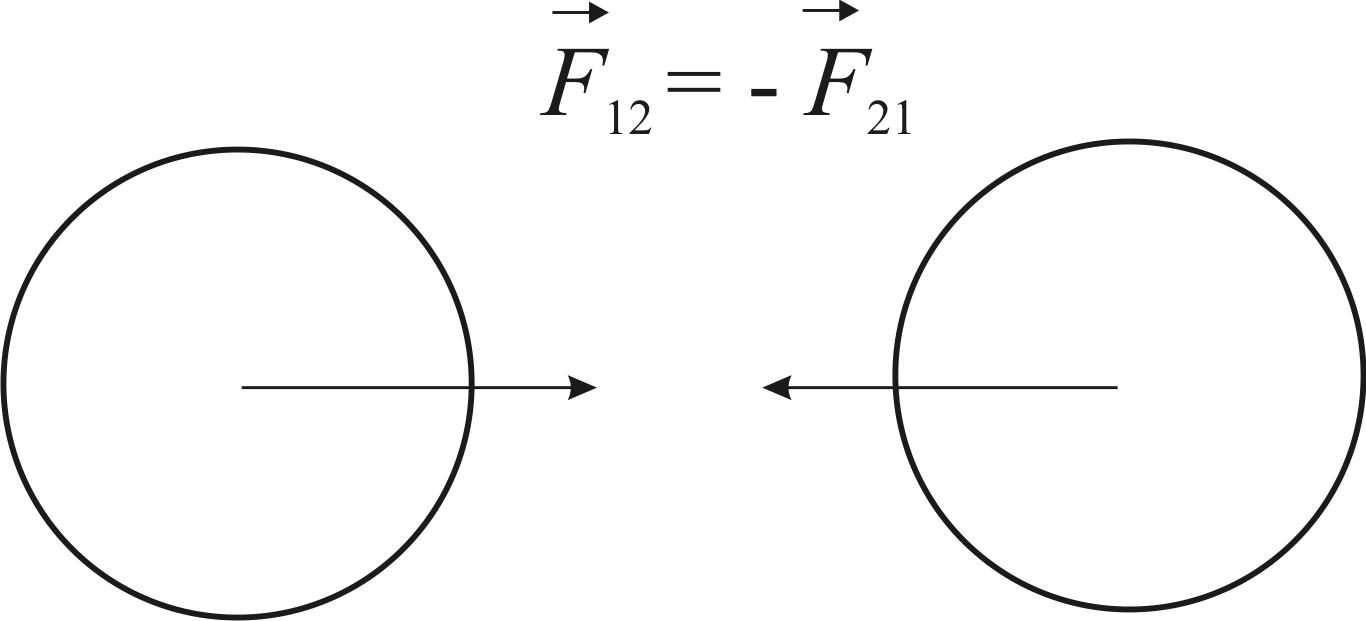
Рис. 1.1. Взаимодействие двух тел
Закон сохранения импульса

Используя второй и третий законы Ньютона, можно получить закон сохранения импульса.

Рассмотрим систему из n тел. К каждому из тел можно применить второй закон Ньютона (1.1). В правой части этого уравнения стоит результирующая сила, действующая на тело. Среди сил различают внутренние и внешние силы.

Внутренними силами называются силы, действующие на тела системы со стороны других тел этой системы.

Внешними называются силы, действующие на тела системы со стороны других тел, не входящих в систему.

Если уравнение (1.1) записать для каждого тела, входящего в рассматриваемую систему из n тел, то получим систему из n уравнений. Если сложить левые и правые части этих уравнений, получим уравнение, которое представляет собой в левой части сумму производных импульсов тел по времени, а в правой части – сумму всех сил, действующих на тела системы. По третьему закону Ньютона, сумма внутренних сил равна нулю. Если система замкнута (внешние силы отсутствуют), или внешние силы компенсируют друг друга
, то векторная сумма внешних сил равна нулю, и, следовательно:

,

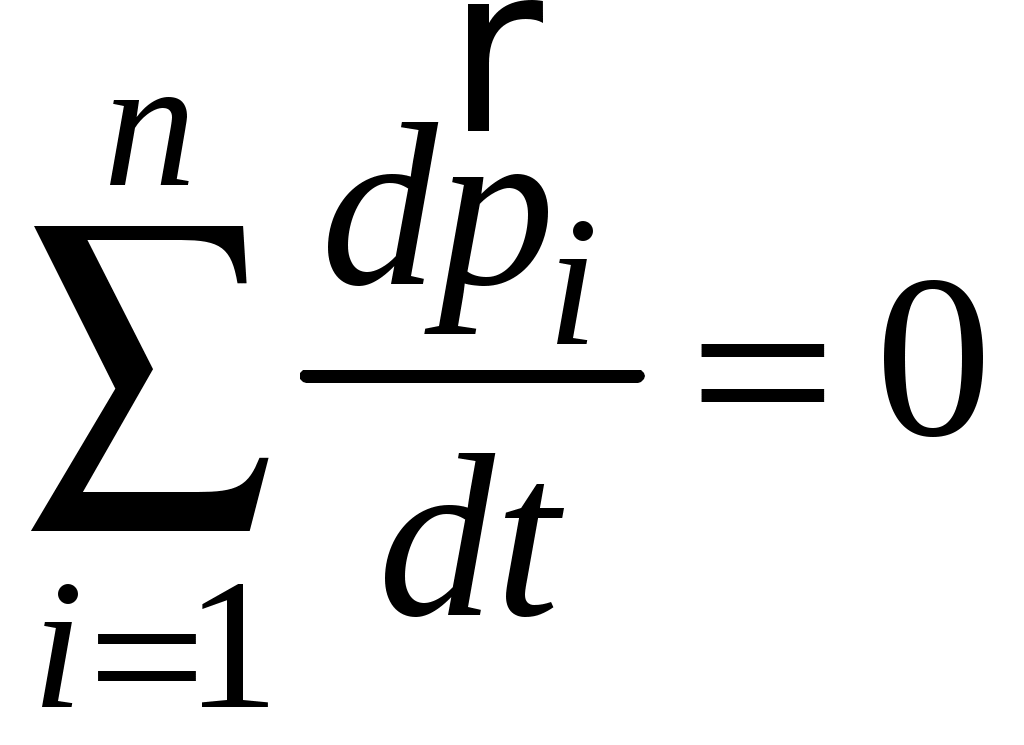а поскольку сумма производных равна производной от суммы, то

.

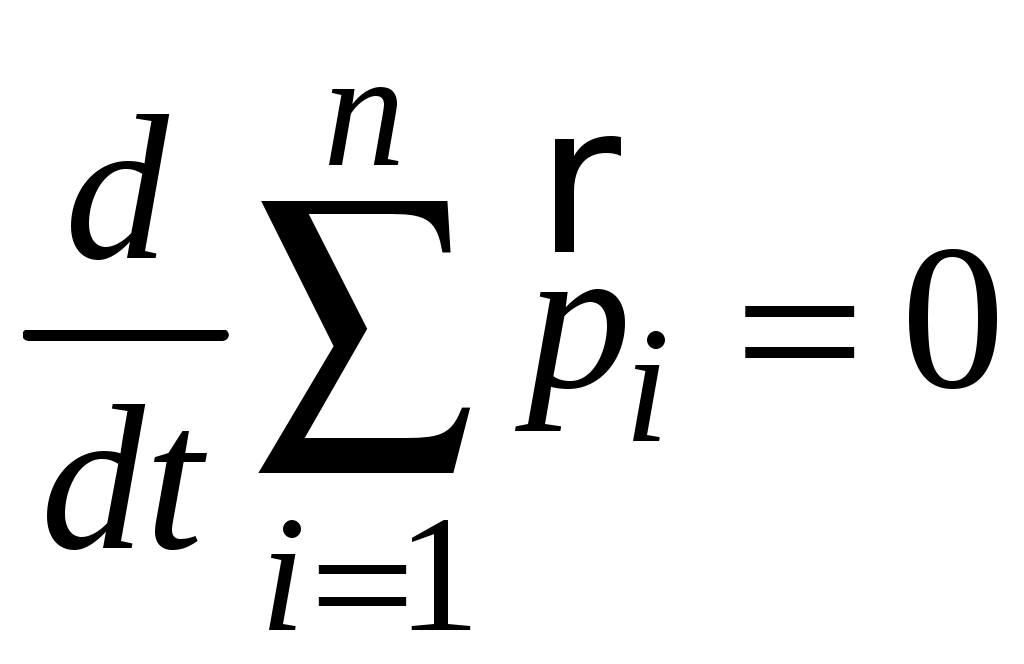Введем понятие импульса системы как векторную сумму импульсов всех тел, входящих в эту систему:

.

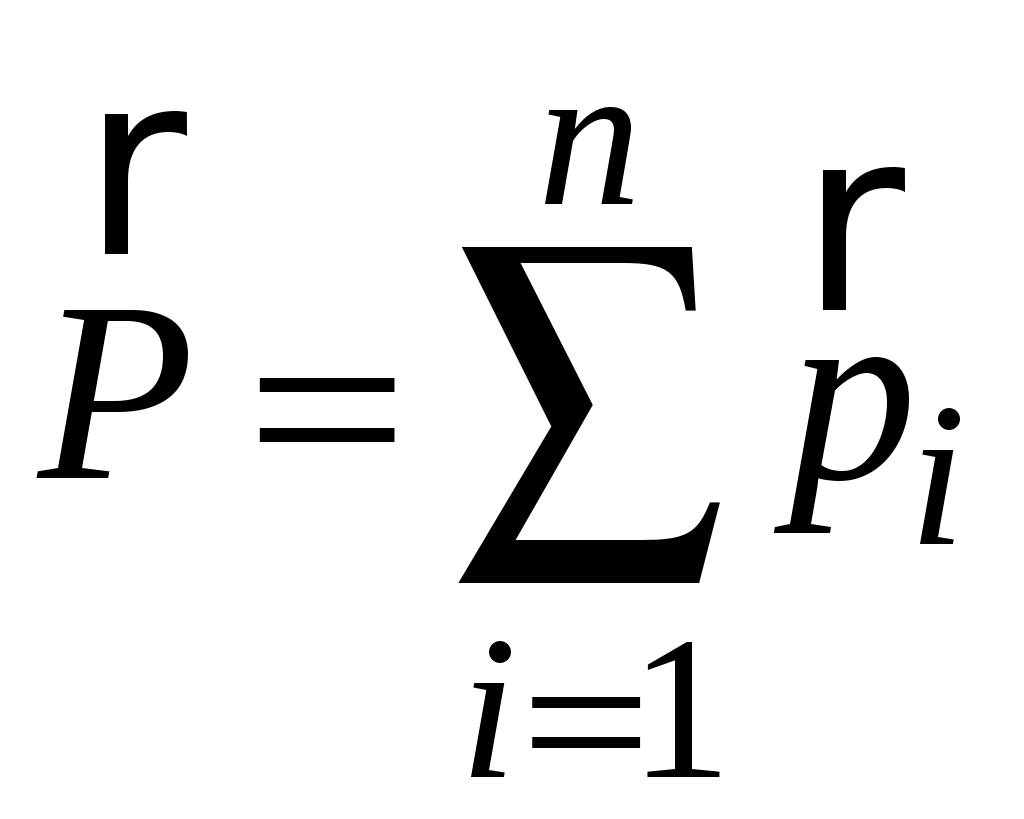Тогда производная по времени от импульса системы равна нулю, т. е.

.

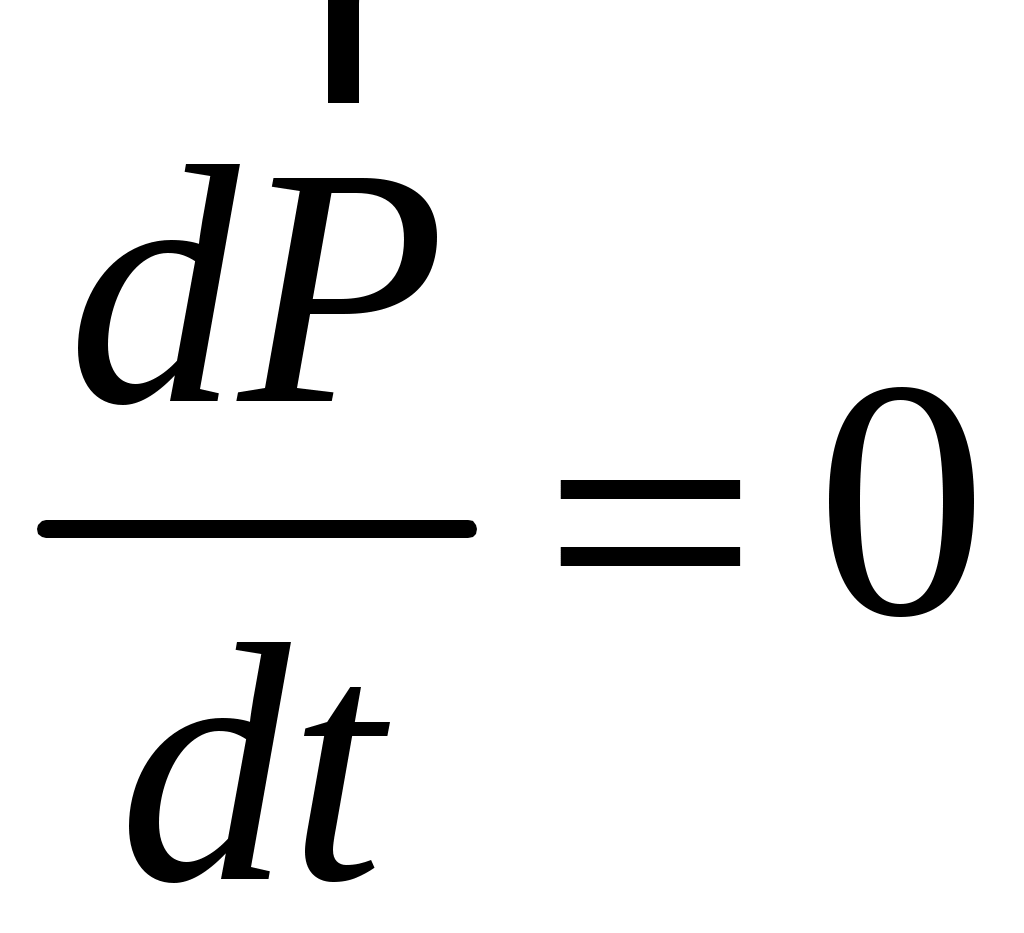Отсюда следует, что

Таким образом, закон сохранения импульса формулируется так: импульс системы сохраняется тогда и только тогда, когда векторная сумма внешних сил, действующих на тела системы, равна нулю.

Консервативные и неконсервативные силы

В механике рассматриваются консервативные и неконсервативные силы. Консервативными называются силы, работа которых не зависит от траектории, а определяется только начальным и конечным положением материальной точки. Силы, не обладающие таким свойством, называются неконсервативными.

Например, сила тяжести и упругая сила – это консервативные силы, а сила трения – неконсервативная сила.

Энергия. Закон сохранения механической энергии

В классической механике рассматривают энергию двух видов: кинетическую и потенциальную.

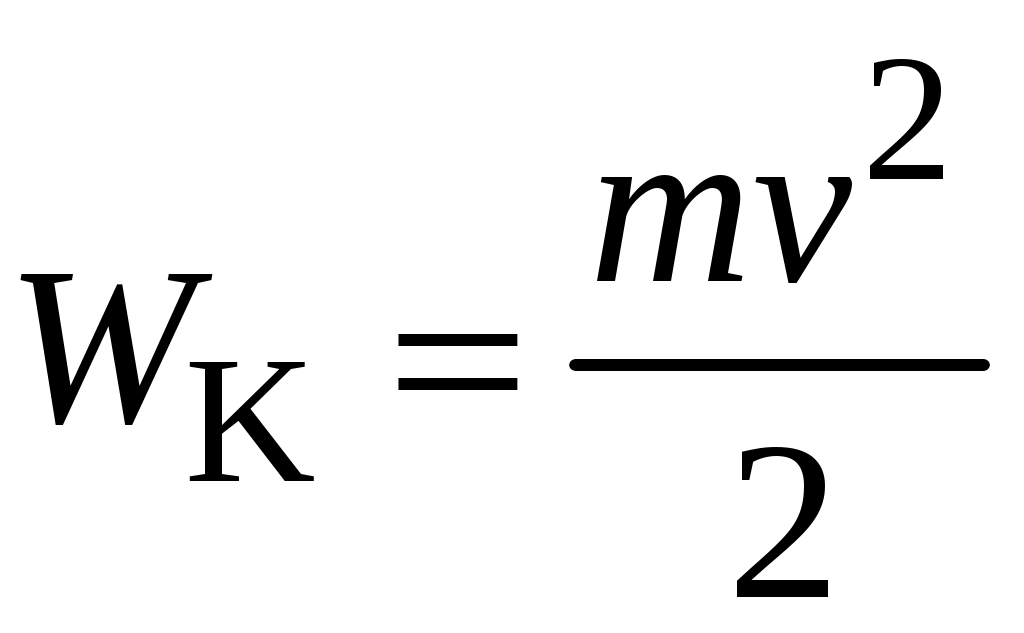Кинетической энергией называется энергия, которой тело обладает вследствие своего движения. Она зависит от скорости и в классической механике (при скоростях, малых по сравнению со скоростью света в вакууме) для поступательно движущегося тела вычисляется по следующей формуле:

.

Потенциальная энергия – это энергия, обусловленная взаимным расположением тел или их частей. Она зависит от координат тела и определяется следующим образом.


Потенциальная энергия – это функция координат, разность значений которой в двух точках равна работе консервативной силы, совершаемой при перемещении тела из одной точки в другую:



Подчеркнем, что понятие потенциальной энергии имеет смысл только для консервативного поля сил!

Между потенциальной энергией тела в поле консервативной силы и самой силой существует связь (вытекающая из приведенного выше определения): минус градиент потенциальной энергии в каждой точке пространства равен вектору силы, действующей на тело:



Важно помнить, что абсолютное значение потенциальной энергии имеет смысл, только если задано начало ее отсчета. В качестве примера приведем выражение для потенциальной энергии тела, поднятого в однородном поле силы тяжести на высоту h:

.

Полная механическая энергия равна сумме кинетической и потенциальной энергий:

.

Полная механическая энергия системы тел сохраняется, если силы, действующие на тела системы, консервативны. Это утверждение и представляет собой закон сохранения полной механической энергии.

Если же в системе есть неконсервативные силы (типа сил трения), работа которых, как правило, отрицательна, то механическая энергия системы будет убывать, переходя в тепло:

;

В данной работе для определения скорости пули используется баллистический маятник. Баллистический маятник – это массивное тело, подвешенное на длинных нитях. В лабораторной работе этим телом является полый металлический цилиндр, частично заполненный пластилином. Обозначим массу этого цилиндра буквой М. В цилиндр стреляют из пружинного пистолета пулей массой m. Пуля, летящая со скоростью v, попадает в цилиндр баллистического маятника и застревает в пластилине. Цилиндр маятника, висевший неподвижно, получает вследствие удара пули некоторый импульс и отклоняется от положения равновесия. Законы сохранения импульса и энергии позволяют связать скорость пули v

Смотрите также файлы