ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 155
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, создаваемую всем проводником, необходимо определить магнитную индукцию, создаваемую отдельными участками проводника  , и проинтегрировать по всему проводнику:
, и проинтегрировать по всему проводнику:
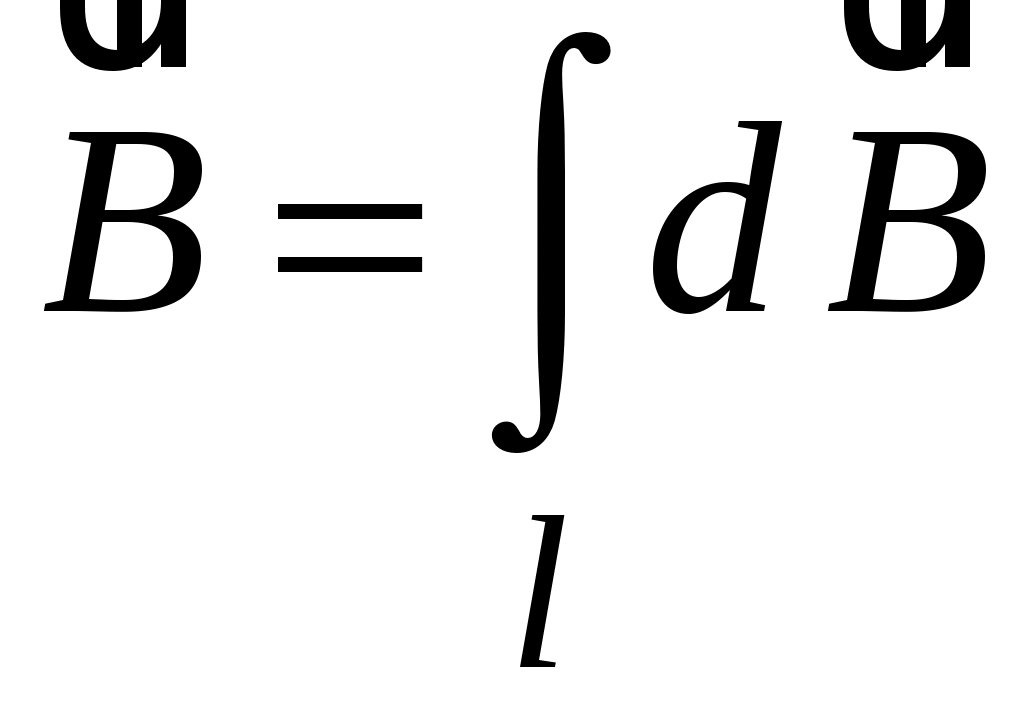 . (5.3)
. (5.3)
Каждый элемент тока, согласно закону Био – Савара – Лапласа, создает магнитное поле с индукцией , определяемой формулой (5.1).
, определяемой формулой (5.1).
Чтобы найти поле в центре тонкого кольца с током, мысленно разобьем его на множество малых участков с током
с током  (рис. 5.2).
(рис. 5.2).
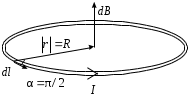
Рис. 5.2. Магнитная индукция в центре кольца с током
Прежде всего, проверим, как направлены векторы , создаваемые каждым участком. Пользуясь правилом правого винта для определения направления
, создаваемые каждым участком. Пользуясь правилом правого винта для определения направления  , легко убедиться, что в центре кольца все векторы
, легко убедиться, что в центре кольца все векторы  направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму
направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму 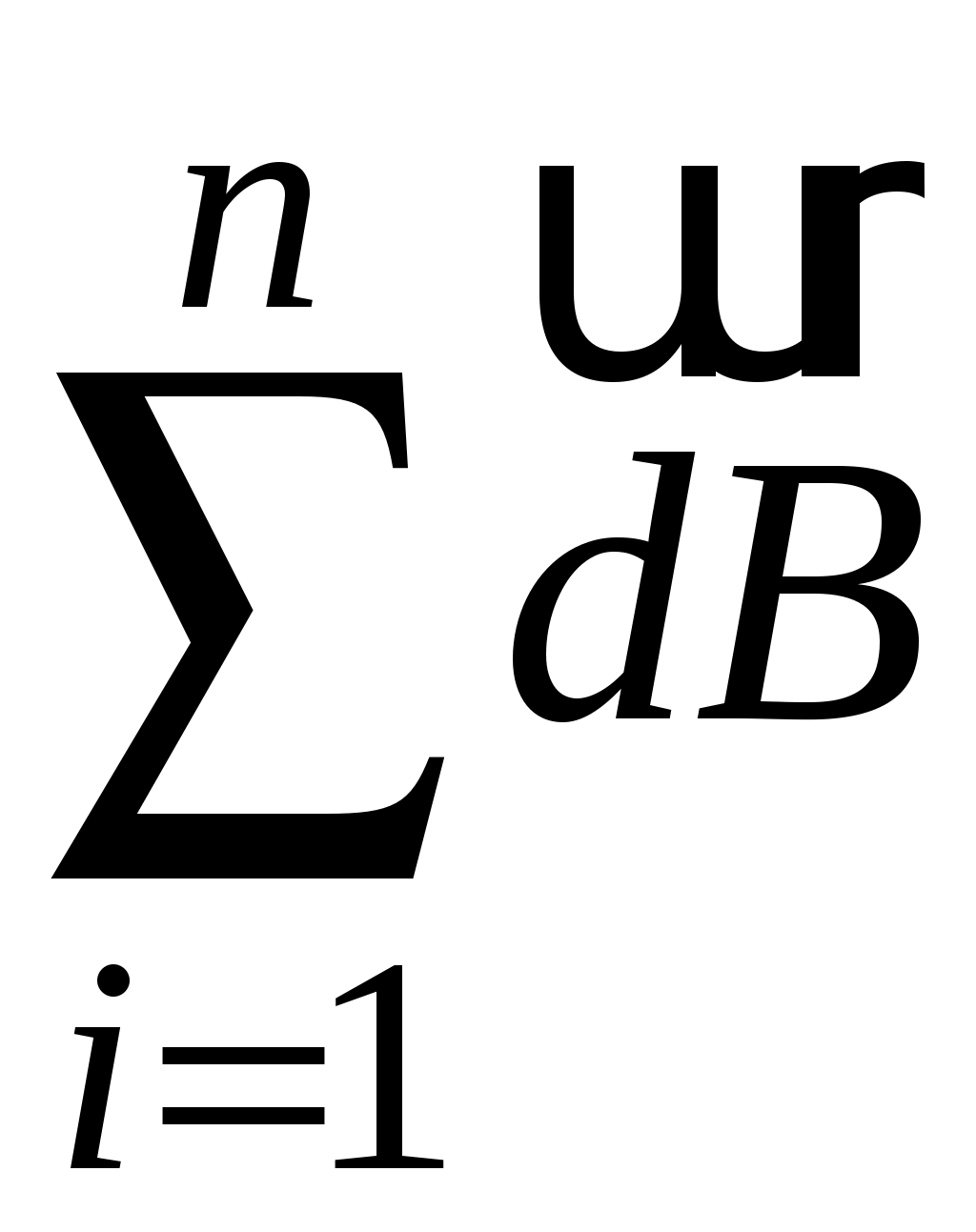 можно заменить арифметической
можно заменить арифметической 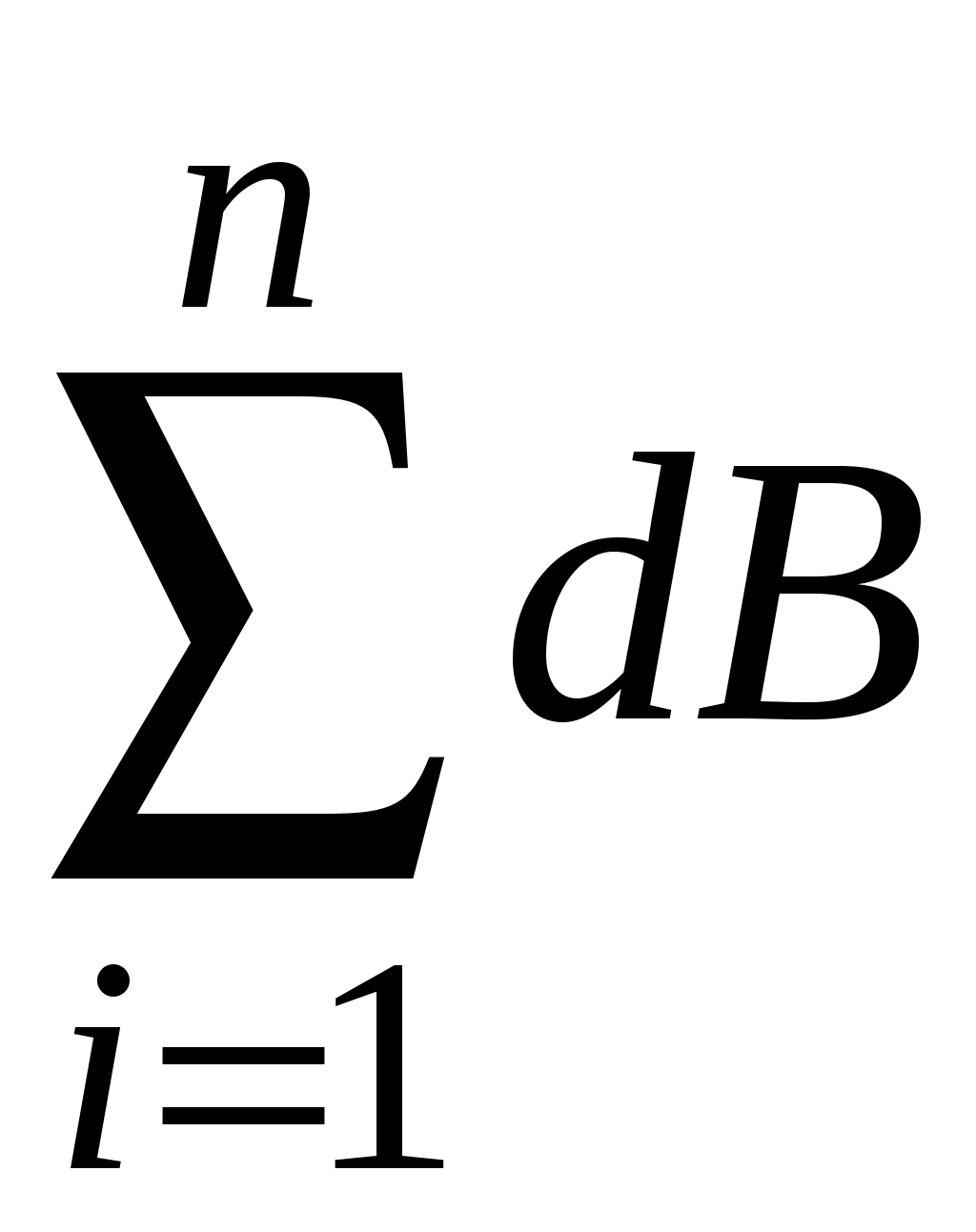 , и для магнитной индукции в центре кольца получим выражение
, и для магнитной индукции в центре кольца получим выражение
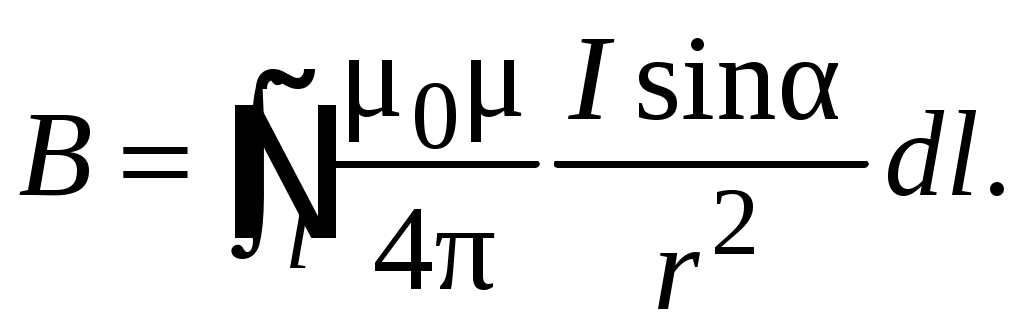 (5.4)
(5.4)
Из геометрии задачи видно, что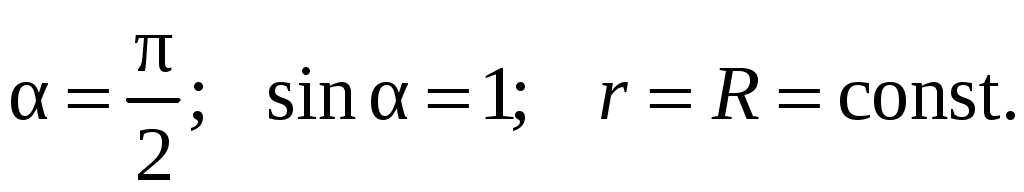 Вынося из-под знака интеграла постоянные величины, получаем:
Вынося из-под знака интеграла постоянные величины, получаем:
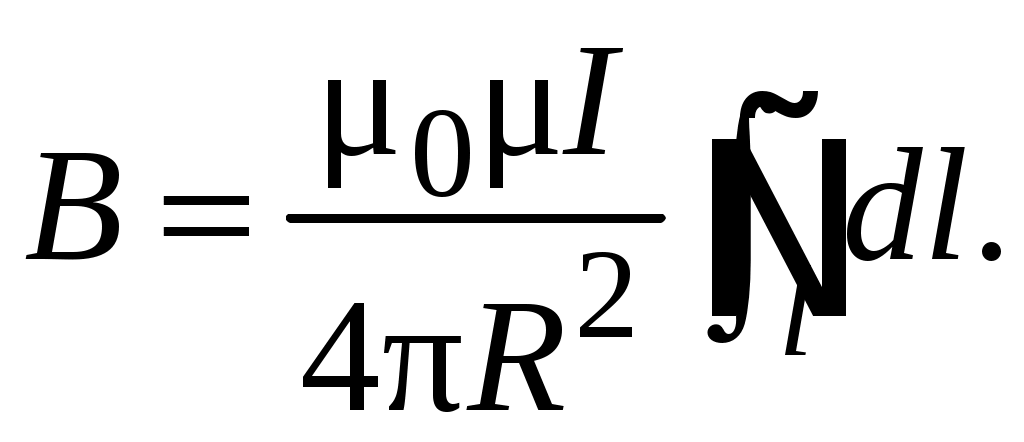 (5.5)
(5.5)
Так как интеграл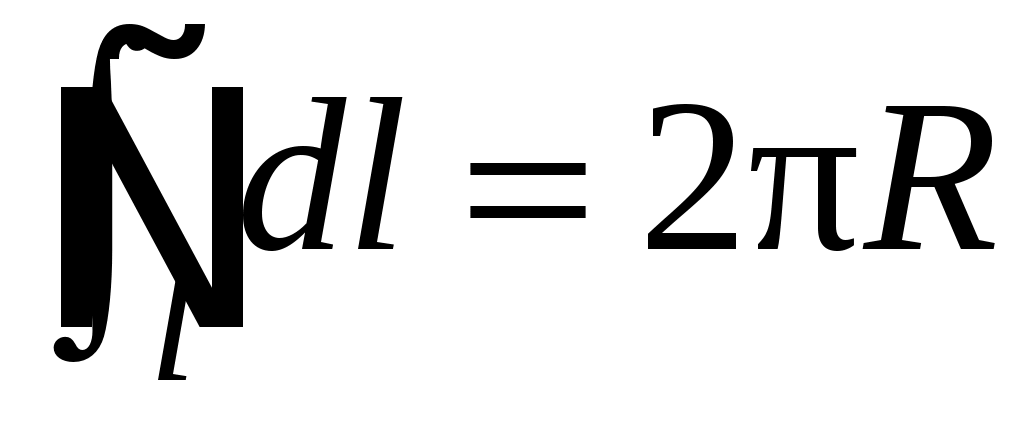 , то индукция в центре кольца находится как
, то индукция в центре кольца находится как
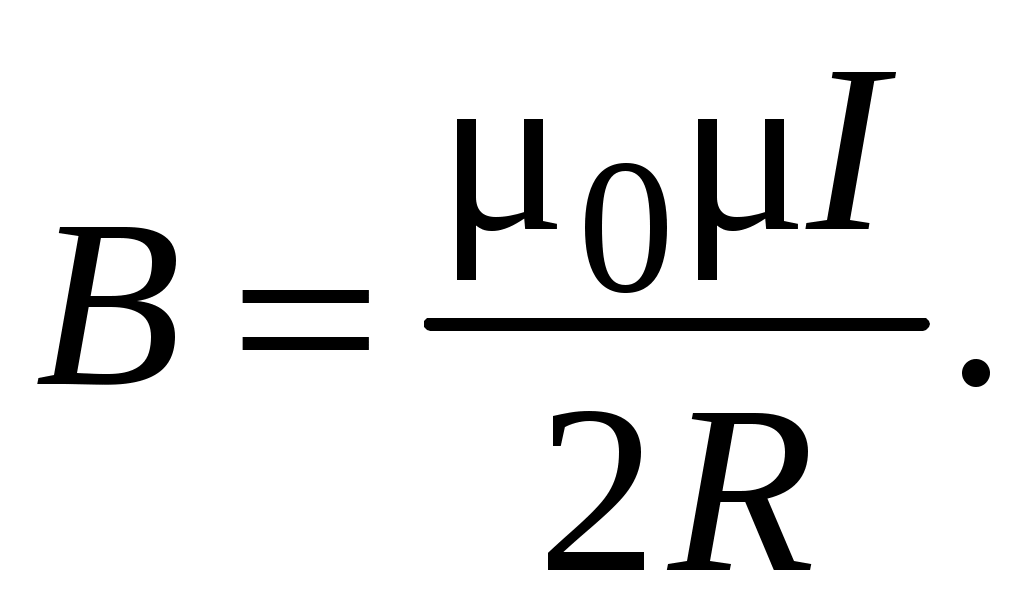 (5.6)
(5.6)
Направление вектора магнитной индукции
на оси кольца с током показано на рис. 5.3.
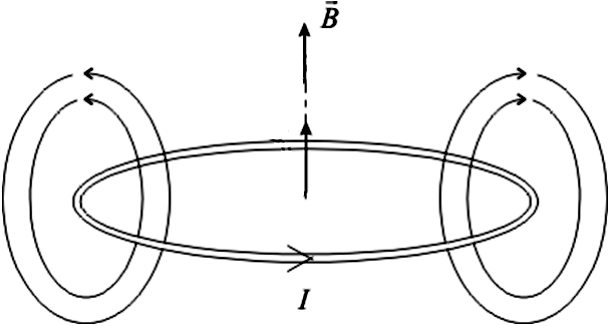
Рис. 5.3. Линии магнитной индукции кольца с током
Вектор магнитной индукции направлен перпендикулярно плоскости кольца, направление вектора
направлен перпендикулярно плоскости кольца, направление вектора  определяется по правилу правого винта для кольцевого тока.
определяется по правилу правого винта для кольцевого тока.
Методика определения магнитного поля Земли
Существование магнитного поля у Земли объясняется токами, протекающими по поверхности жидкого металлического ядра Земли, а также намагниченностью горных пород. Положение магнитных полюсов Земли не совпадает с положением географических полюсов: вблизи северного географического полюса находится южный магнитный полюс S, а северный магнитный полюс N находится в Антарктиде вблизи южного географического полюса. Линии напряженности магнитного поля Земли показаны на рис. 5.4.
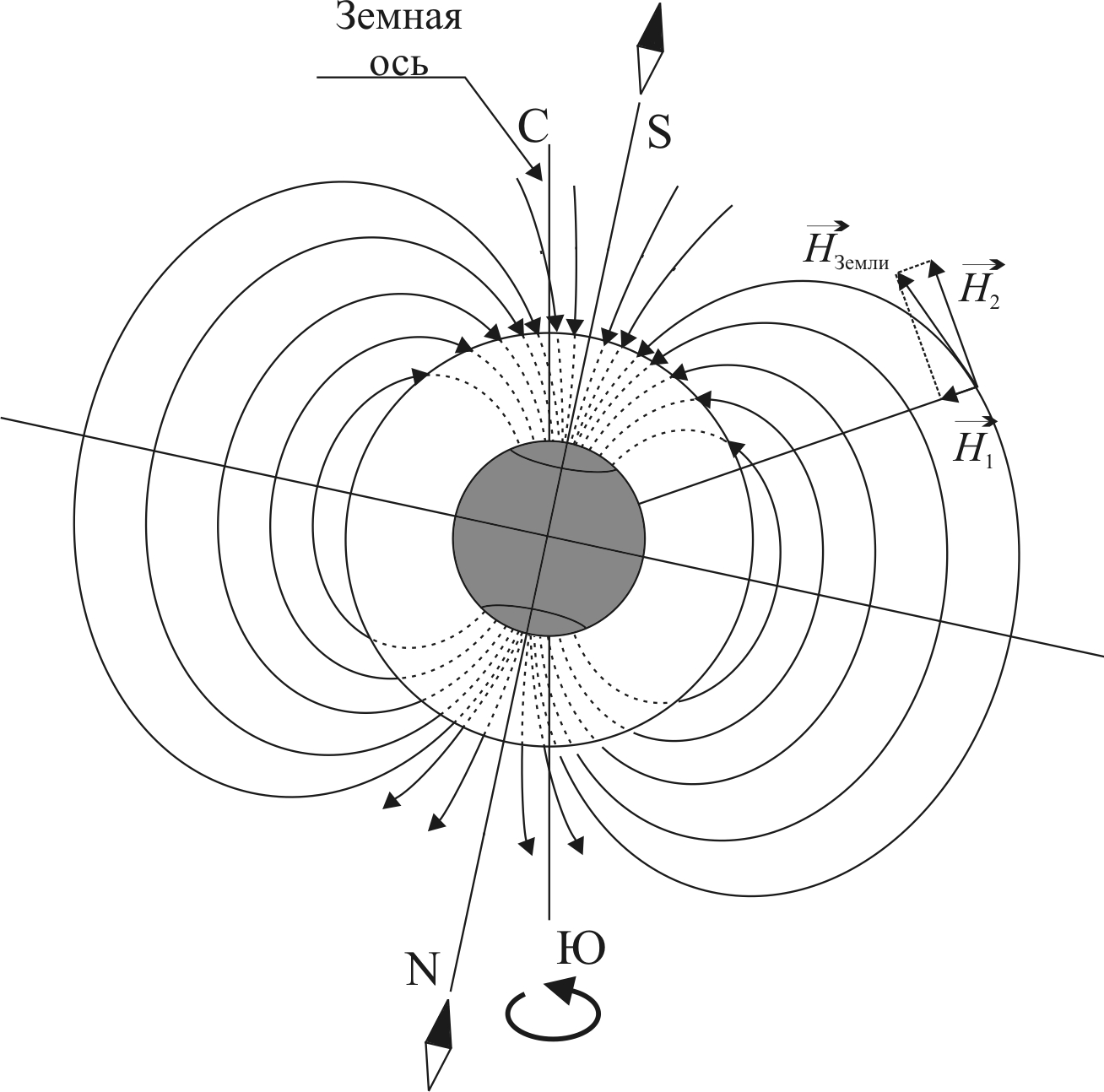
Рис. 5.4. Линии напряженности магнитного поля Земли:
 – вертикальная составляющая вектора напряженности;
– вертикальная составляющая вектора напряженности; 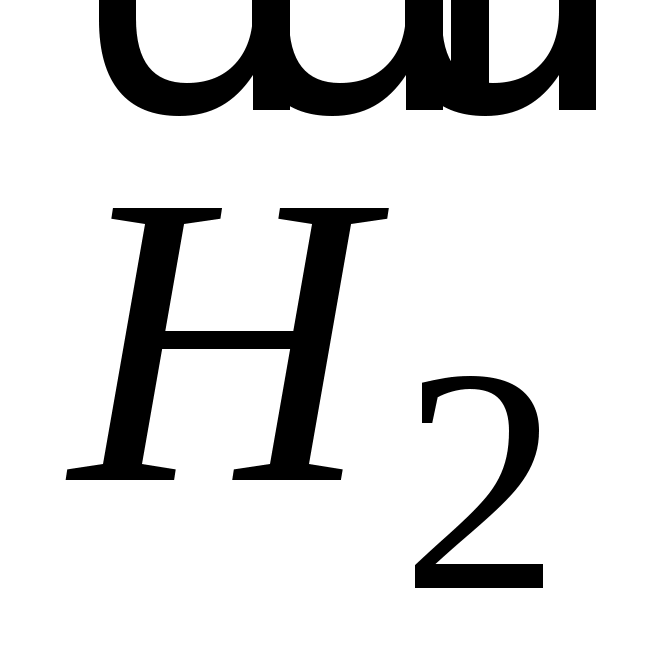 – горизонтальная составляющая вектора напряженности
– горизонтальная составляющая вектора напряженности
Плоскость, перпендикулярная к поверхности Земли, в которой устанавливается магнитная стрелка компаса, называют плоскостью геомагнитного меридиана данного места, а линию, по которой поверхность Земли пересекается с плоскостью меридиана, называют геомагнитным меридианом. Угол между геомагнитным и географическим меридианами называют магнитным склонением, эта величина зависит от географической широты местности и указана на картах.
На практике с помощью магнитной стрелки наиболее удобно определять горизонтальную составляющую вектора напряженности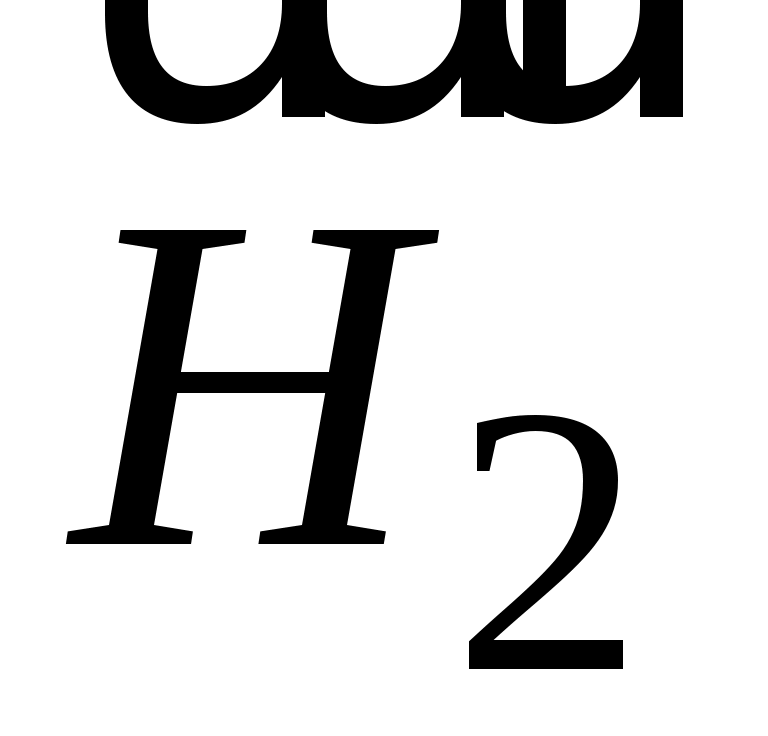 , направленную по касательной к геомагнитному меридиану.
, направленную по касательной к геомагнитному меридиану.
Лабораторная установка для определения горизонтальной составляющей магнитного поля Земли (рис. 5.5) состоит из двух катушек с одинаковым числом витков N, расположенных соосно на расстоянии друг от друга, равном радиусу катушки (катушки Гельмгольца), и компаса, установленного в центре системы на осевой линии. До включения тока в катушках необходимо сориентировать систему так, чтобы катушки располагались параллельно плоскости магнитного меридиана (рис. 5.5, а). При включении тока магнитное поле катушек
магнитного поля Земли (рис. 5.5) состоит из двух катушек с одинаковым числом витков N, расположенных соосно на расстоянии друг от друга, равном радиусу катушки (катушки Гельмгольца), и компаса, установленного в центре системы на осевой линии. До включения тока в катушках необходимо сориентировать систему так, чтобы катушки располагались параллельно плоскости магнитного меридиана (рис. 5.5, а). При включении тока магнитное поле катушек 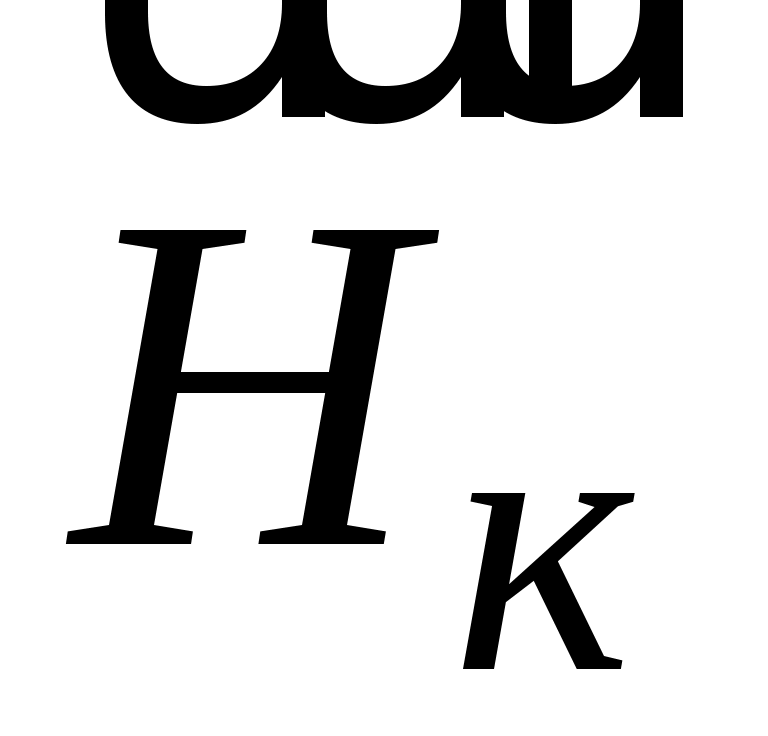 , направленное горизонтально, отклоняет магнитную стрелку компаса от плоскости магнитного меридиана на угол
, направленное горизонтально, отклоняет магнитную стрелку компаса от плоскости магнитного меридиана на угол 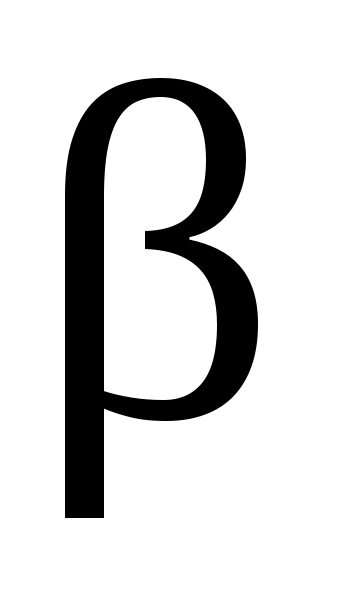 (рис. 5.5, б). Суммарное магнитное поле
(рис. 5.5, б). Суммарное магнитное поле 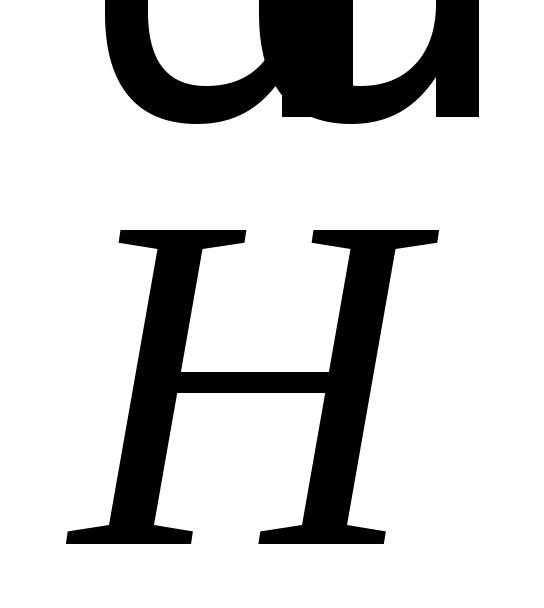 , вдоль которого устанавливается магнитная стрелка, может быть найдено как
, вдоль которого устанавливается магнитная стрелка, может быть найдено как
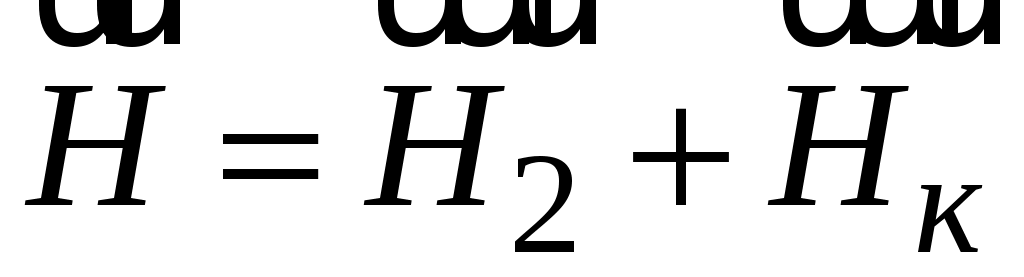 .
.
Из геометрических соображений можно выразить величину горизонтальной составляющей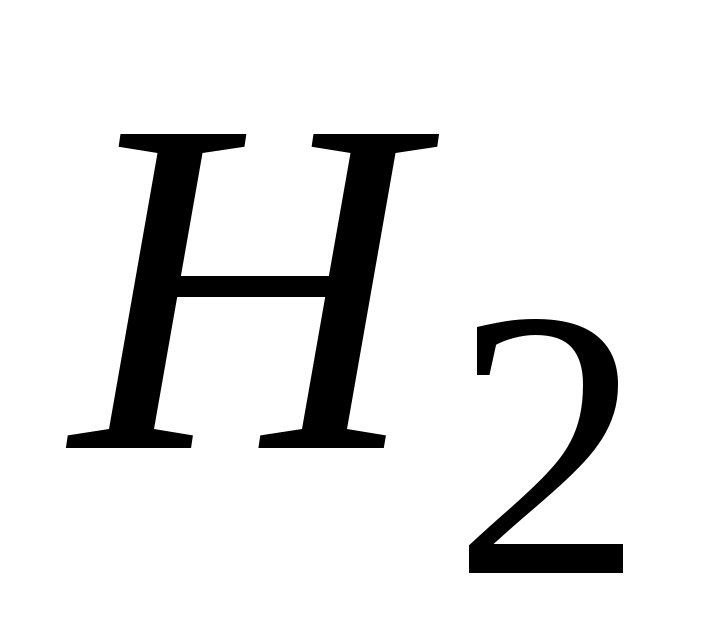 через известные величины
через известные величины 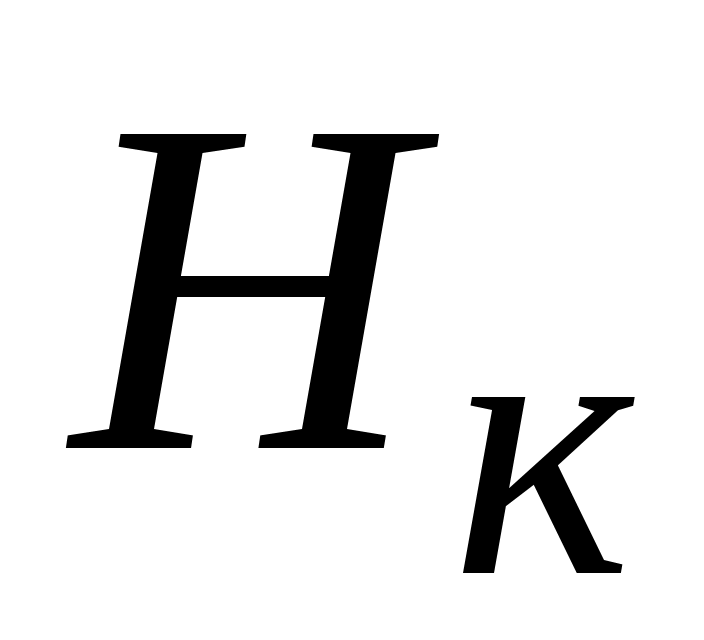 и
и 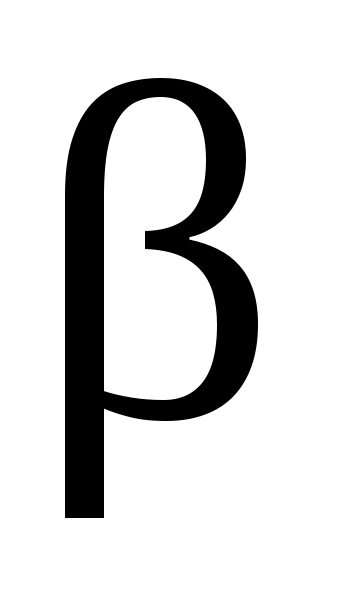 (рис. 5.5, б):
(рис. 5.5, б):
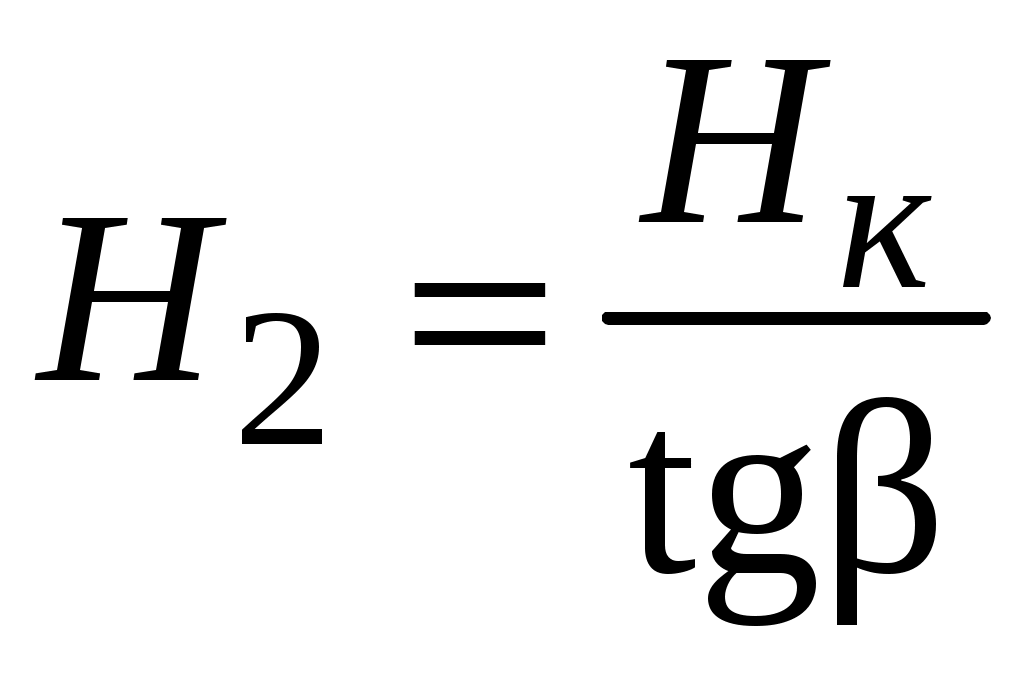 . (5.7)
. (5.7)
Магнитное поле катушек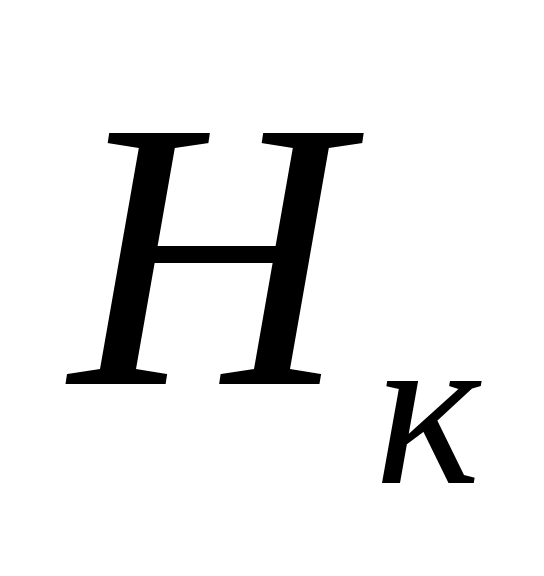 на оси, проходящей через центры катушек в точке, равноудаленной от плоскостей обеих катушек, вычисляется по формуле
на оси, проходящей через центры катушек в точке, равноудаленной от плоскостей обеих катушек, вычисляется по формуле
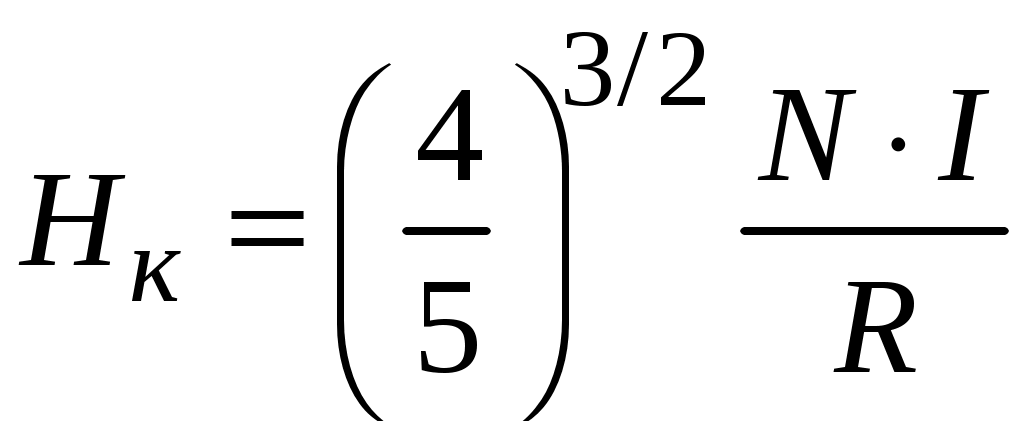 , (5.8)
, (5.8)
где N – число витков в катушке; I – протекающий по катушке ток; R – радиус катушки.
а) б)
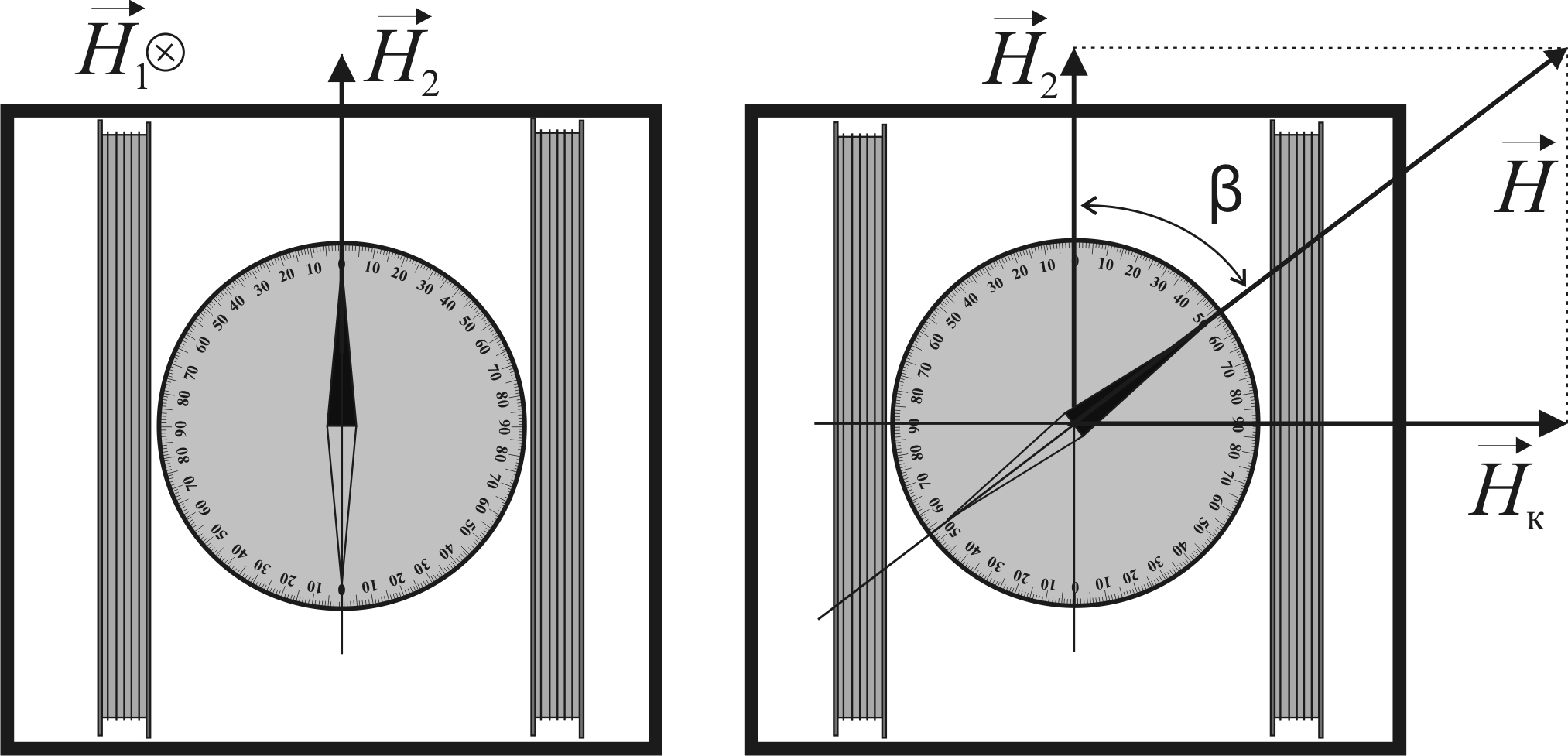
Рис. 5.5. Лабораторная установка для определения горизонтальной
составляющей магнитного поля Земли (вид сверху)
Чтобы повысить точность измерений, угол отклонения магнитной стрелки компаса измеряют дважды, изменяя направление тока в катушках на противоположное, при этом магнитная стрелка сначала отклоняется в одну сторону на угол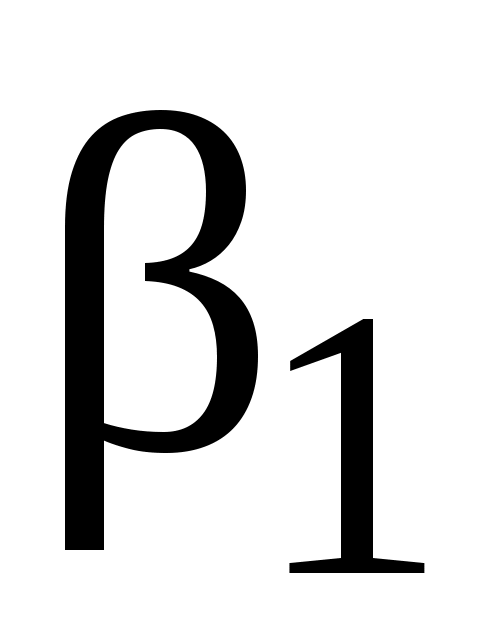 , а затем – в противоположную сторону на угол
, а затем – в противоположную сторону на угол 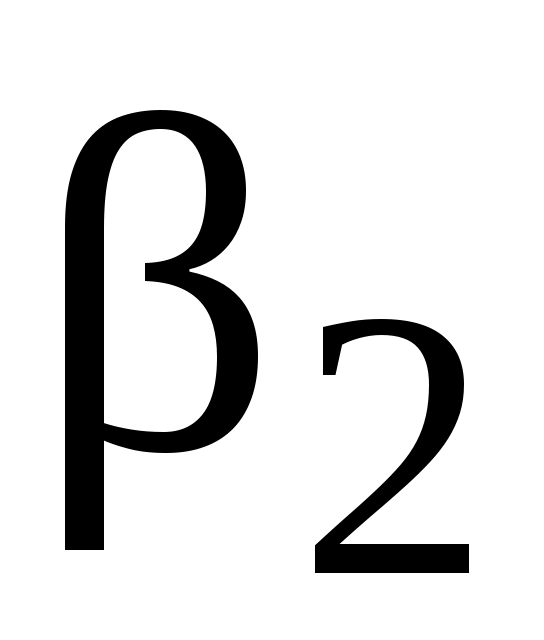 . Окончательно горизонтальная составляющая магнитного поля Земли может быть определена из выражения:
. Окончательно горизонтальная составляющая магнитного поля Земли может быть определена из выражения:
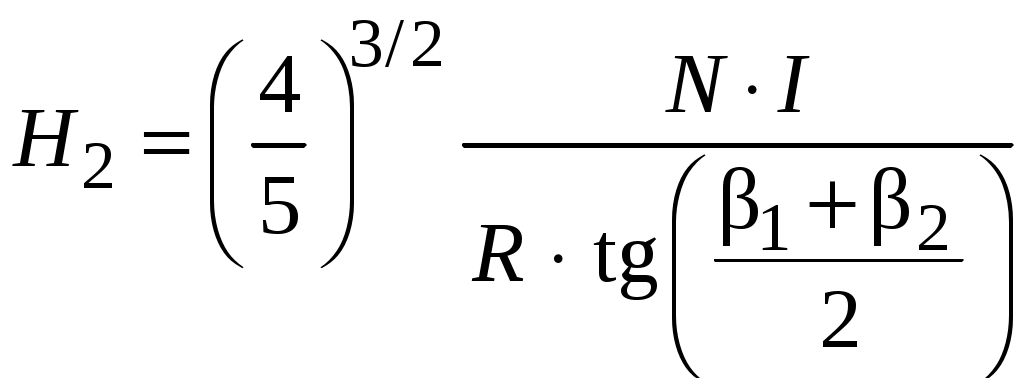 . (5.9)
. (5.9)
Порядок выполнения работы
Таблица 5.1
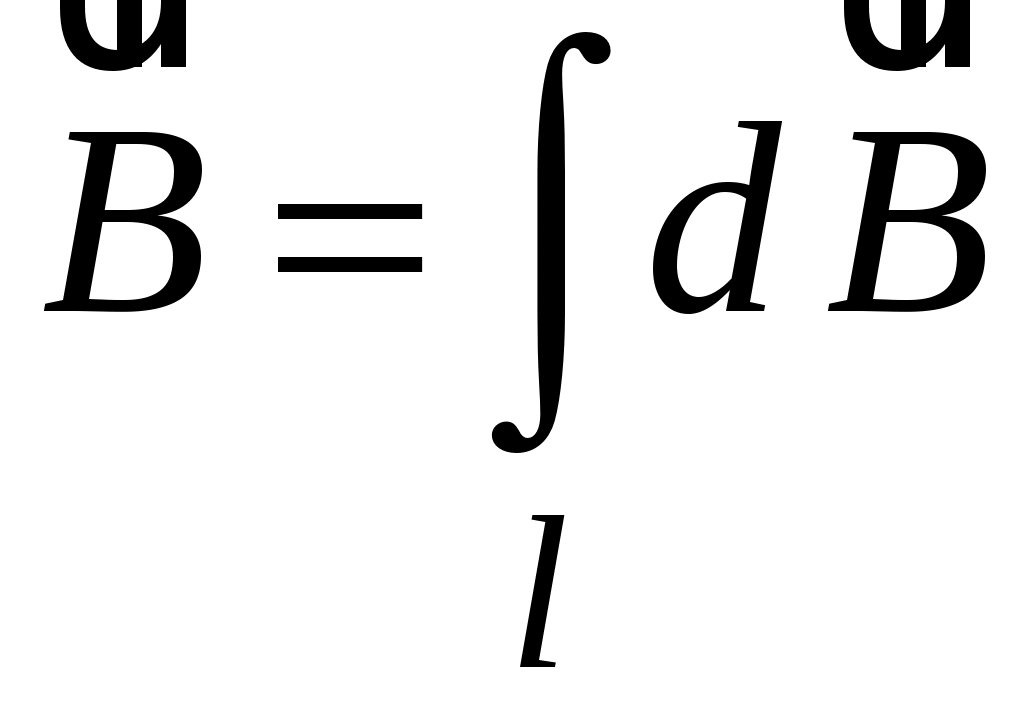 . (5.3)
. (5.3)Каждый элемент тока, согласно закону Био – Савара – Лапласа, создает магнитное поле с индукцией
Чтобы найти поле в центре тонкого кольца с током, мысленно разобьем его на множество малых участков

Рис. 5.2. Магнитная индукция в центре кольца с током
Прежде всего, проверим, как направлены векторы
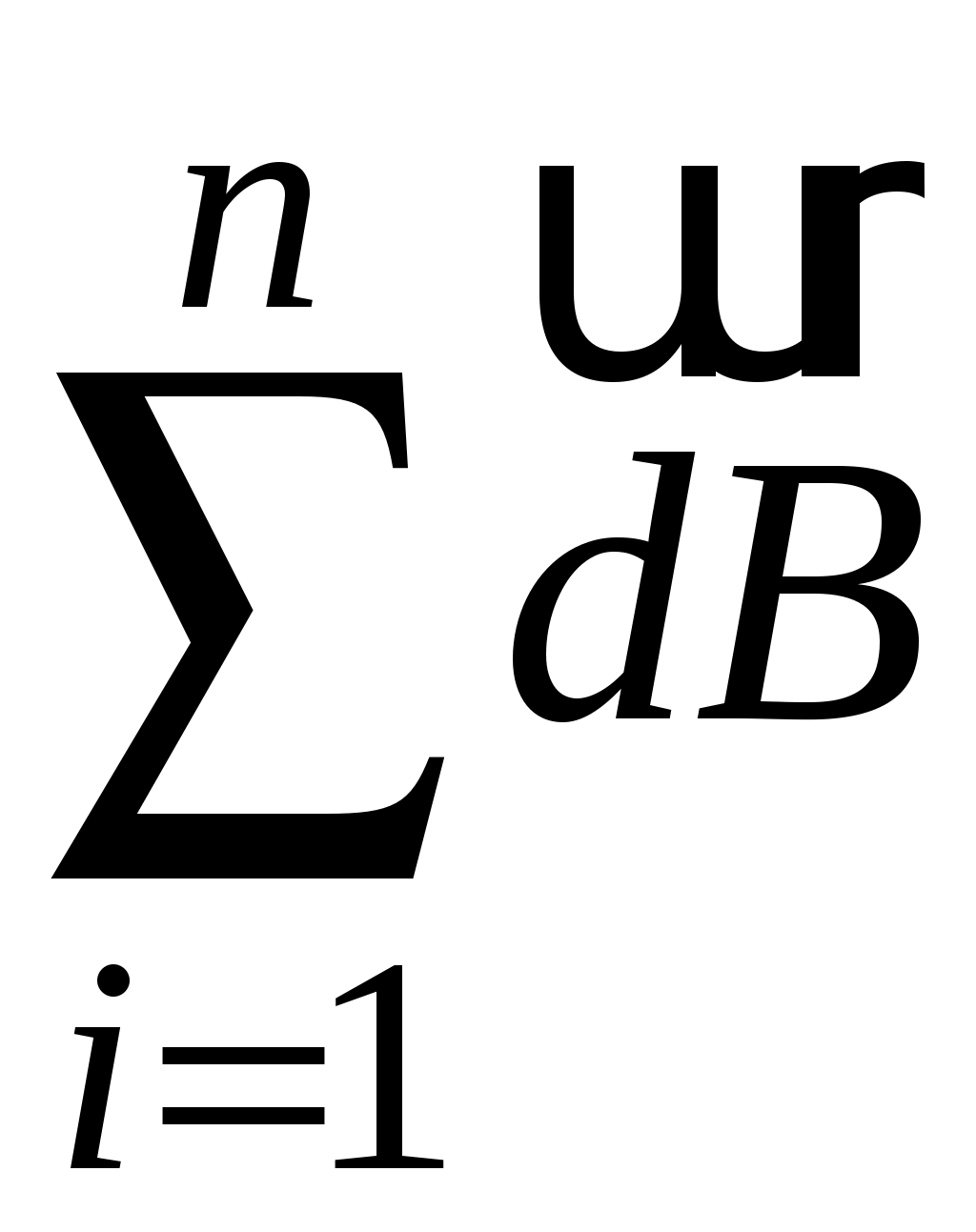 можно заменить арифметической
можно заменить арифметической 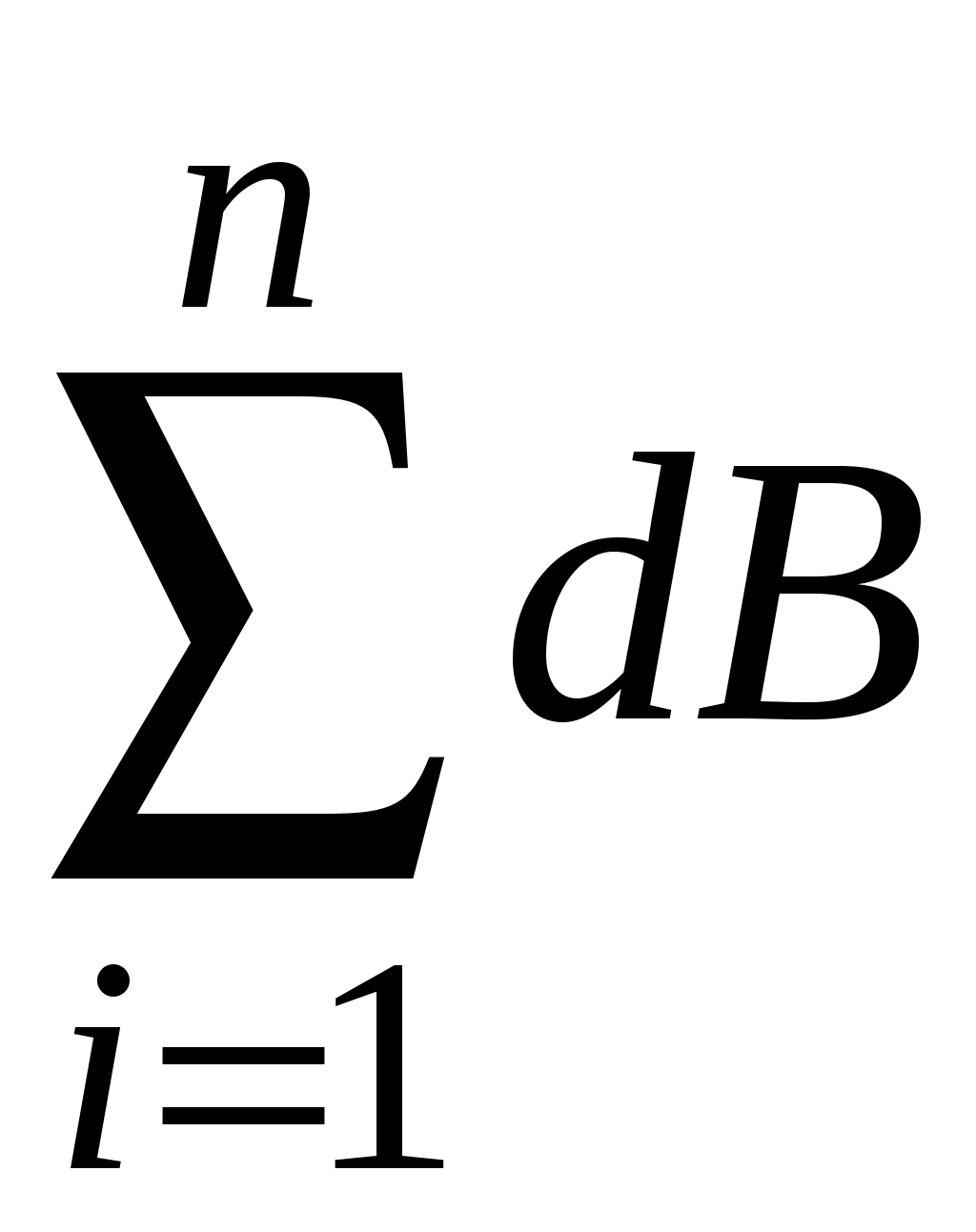 , и для магнитной индукции в центре кольца получим выражение
, и для магнитной индукции в центре кольца получим выражение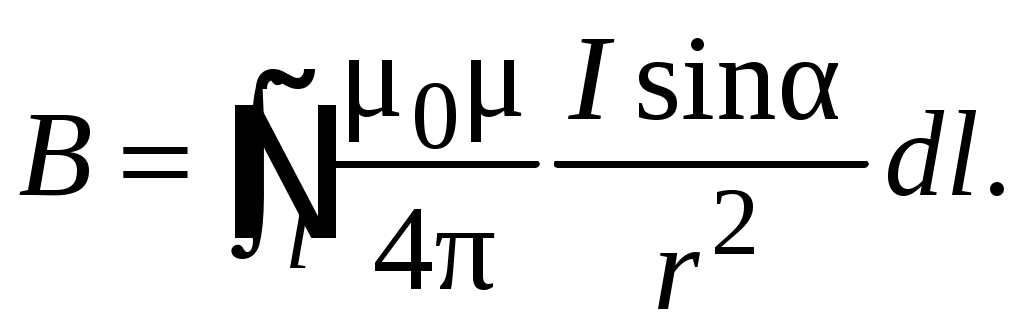 (5.4)
(5.4)Из геометрии задачи видно, что
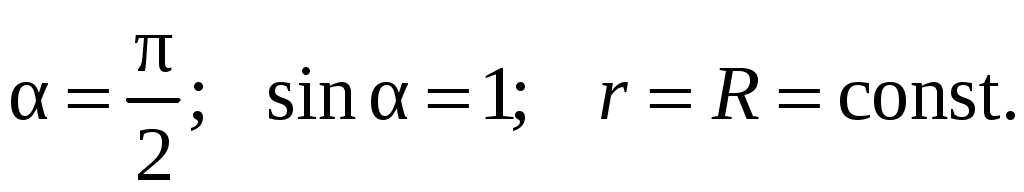 Вынося из-под знака интеграла постоянные величины, получаем:
Вынося из-под знака интеграла постоянные величины, получаем: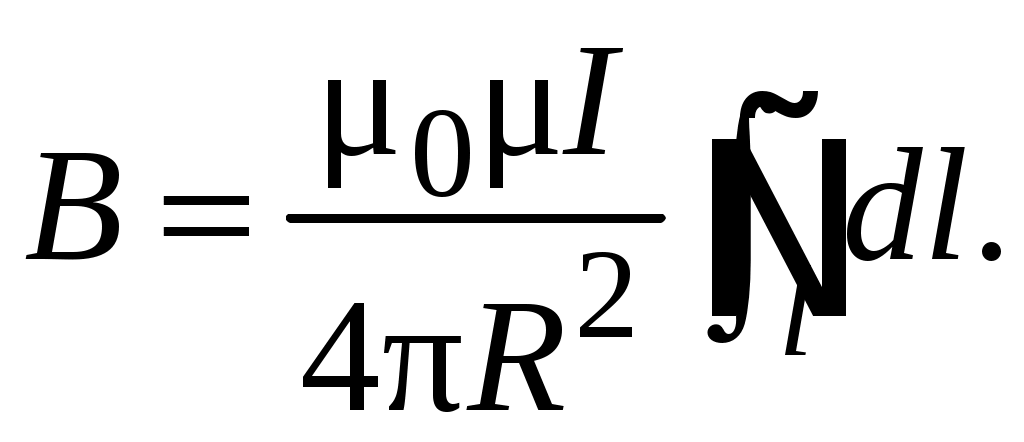 (5.5)
(5.5)Так как интеграл
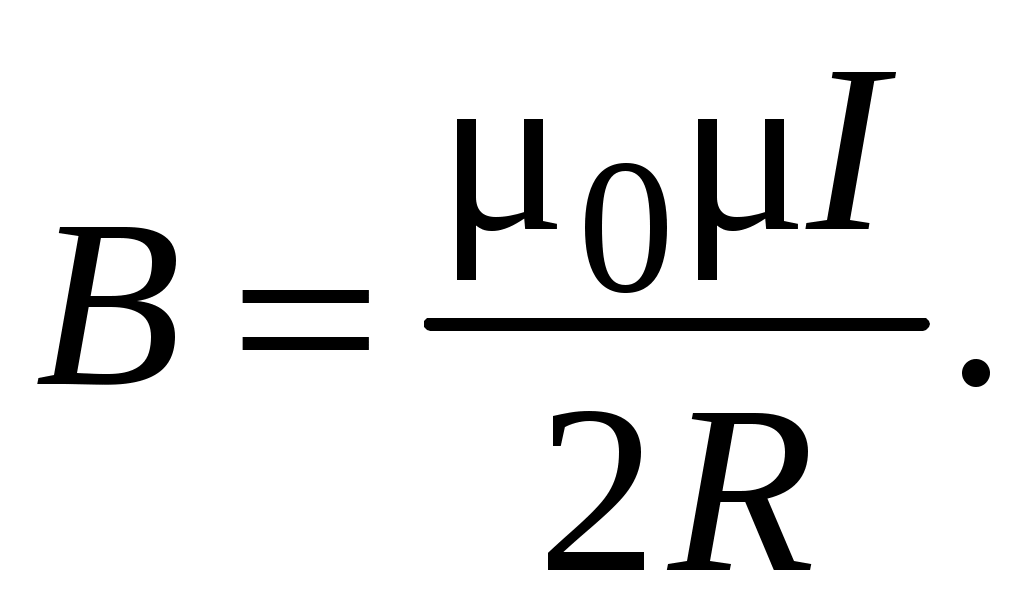 (5.6)
(5.6)Направление вектора магнитной индукции
на оси кольца с током показано на рис. 5.3.

Рис. 5.3. Линии магнитной индукции кольца с током
Вектор магнитной индукции
Методика определения магнитного поля Земли
Существование магнитного поля у Земли объясняется токами, протекающими по поверхности жидкого металлического ядра Земли, а также намагниченностью горных пород. Положение магнитных полюсов Земли не совпадает с положением географических полюсов: вблизи северного географического полюса находится южный магнитный полюс S, а северный магнитный полюс N находится в Антарктиде вблизи южного географического полюса. Линии напряженности магнитного поля Земли показаны на рис. 5.4.

Рис. 5.4. Линии напряженности магнитного поля Земли:
Плоскость, перпендикулярная к поверхности Земли, в которой устанавливается магнитная стрелка компаса, называют плоскостью геомагнитного меридиана данного места, а линию, по которой поверхность Земли пересекается с плоскостью меридиана, называют геомагнитным меридианом. Угол между геомагнитным и географическим меридианами называют магнитным склонением, эта величина зависит от географической широты местности и указана на картах.
На практике с помощью магнитной стрелки наиболее удобно определять горизонтальную составляющую вектора напряженности
Лабораторная установка для определения горизонтальной составляющей
Из геометрических соображений можно выразить величину горизонтальной составляющей
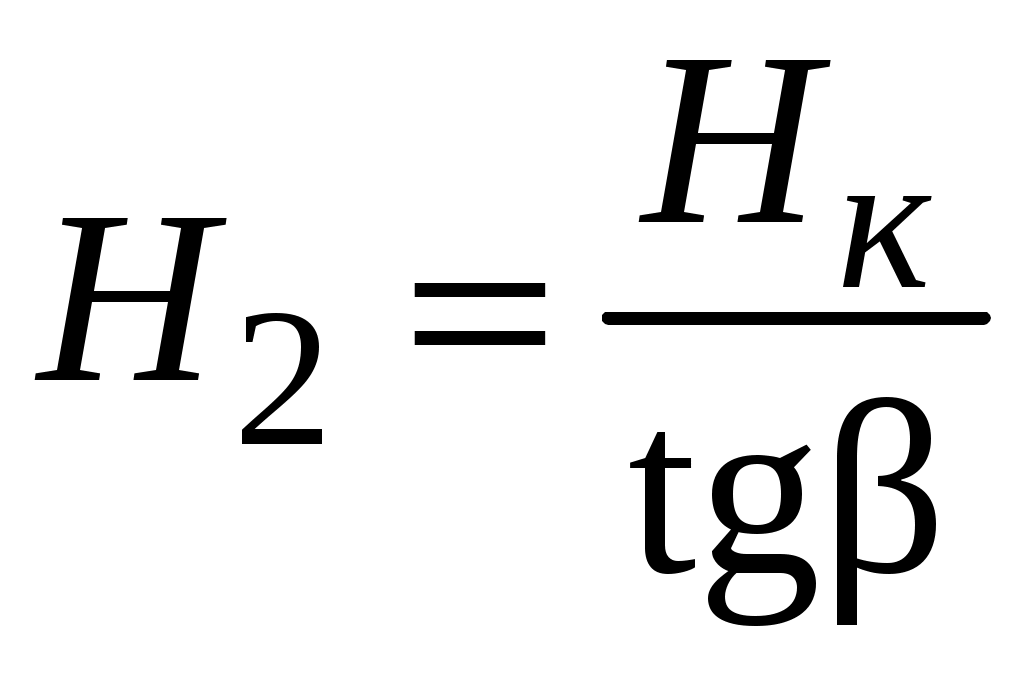 . (5.7)
. (5.7)Магнитное поле катушек
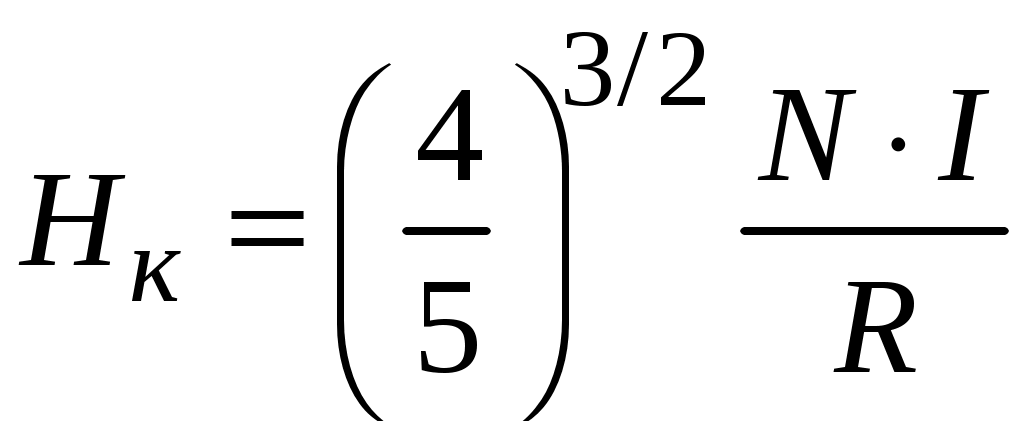 , (5.8)
, (5.8)где N – число витков в катушке; I – протекающий по катушке ток; R – радиус катушки.
а) б)

Рис. 5.5. Лабораторная установка для определения горизонтальной
составляющей магнитного поля Земли (вид сверху)
Чтобы повысить точность измерений, угол отклонения магнитной стрелки компаса измеряют дважды, изменяя направление тока в катушках на противоположное, при этом магнитная стрелка сначала отклоняется в одну сторону на угол
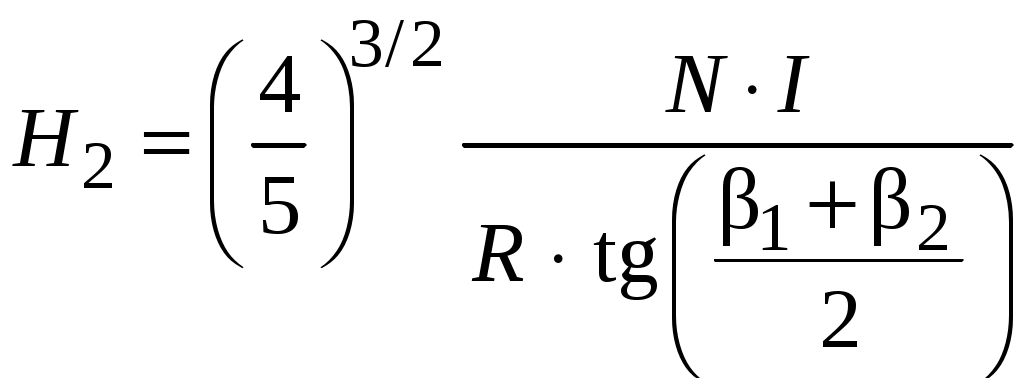 . (5.9)
. (5.9)Порядок выполнения работы
-
При отсутствии тока в катушках сориентируйте установку так, чтобы магнитная стрелка компаса была параллельна плоскостям катушек (установка должна находиться вдали от массивных металлических предметов и проводов с электрическим током). -
Включите прибор и установите переключателем на передней панели минимальное значение тока в катушках, при этом стрелка компаса отклонится на некоторый угол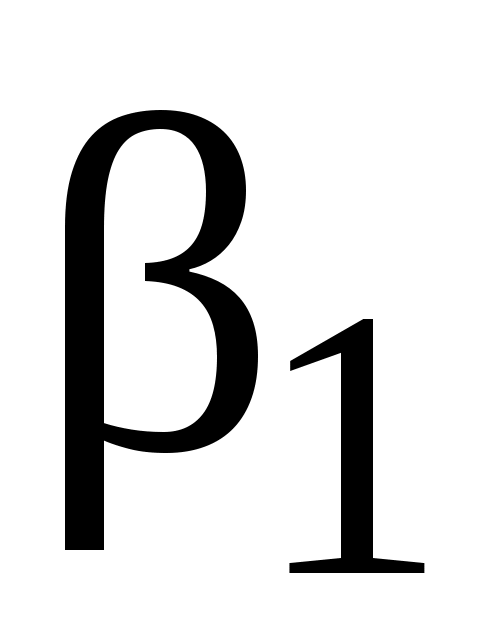 , измерьте значение этого угла в градусах, результаты измерений занесите в табл. 5.1.
, измерьте значение этого угла в градусах, результаты измерений занесите в табл. 5.1. -
Переключателем измените направление тока в катушках и измерьте значение угла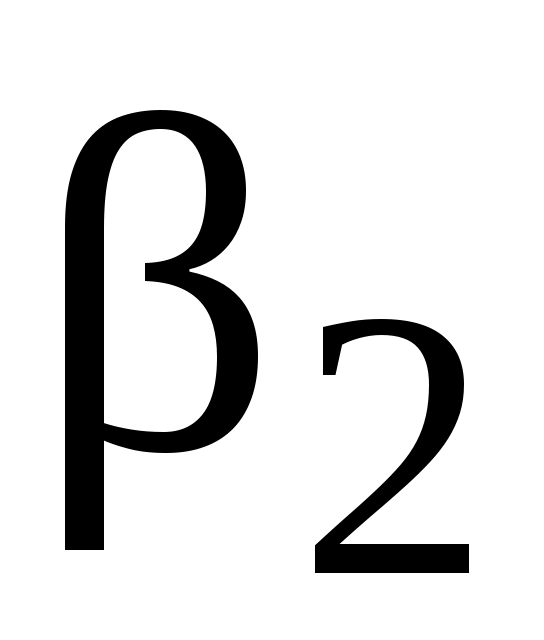 , результаты измерений занесите в табл. 5.1.
, результаты измерений занесите в табл. 5.1. -
Проведите измерения углов отклонения магнитной стрелки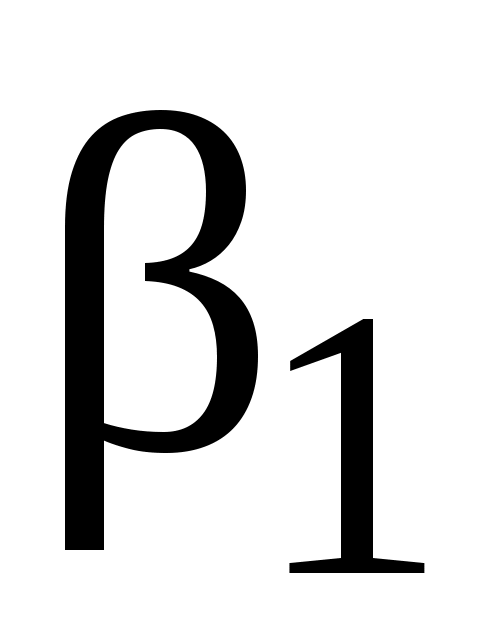 и
и 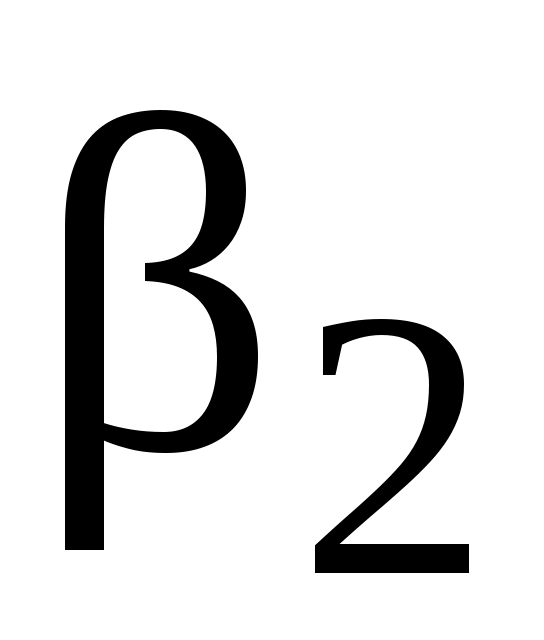 при других значениях тока в катушках и результаты измерений занесите в табл. 5.1.
при других значениях тока в катушках и результаты измерений занесите в табл. 5.1. -
Вычислите значение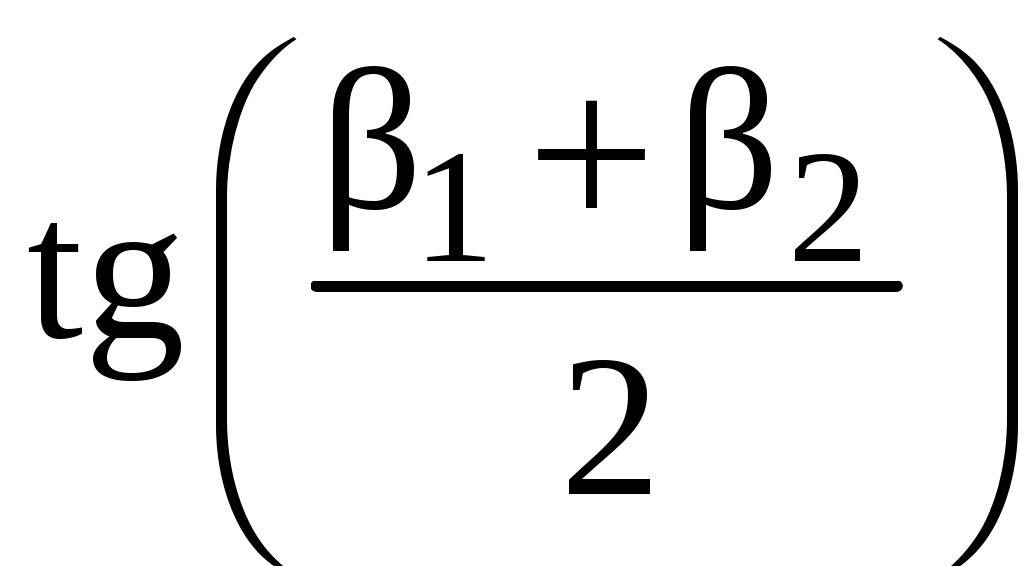 и значение горизонтальной составляющей напряженности магнитного поля
и значение горизонтальной составляющей напряженности магнитного поля  по формуле (5.9).
по формуле (5.9). -
Определите среднее значение горизонтальной составляющей напряженности магнитного поля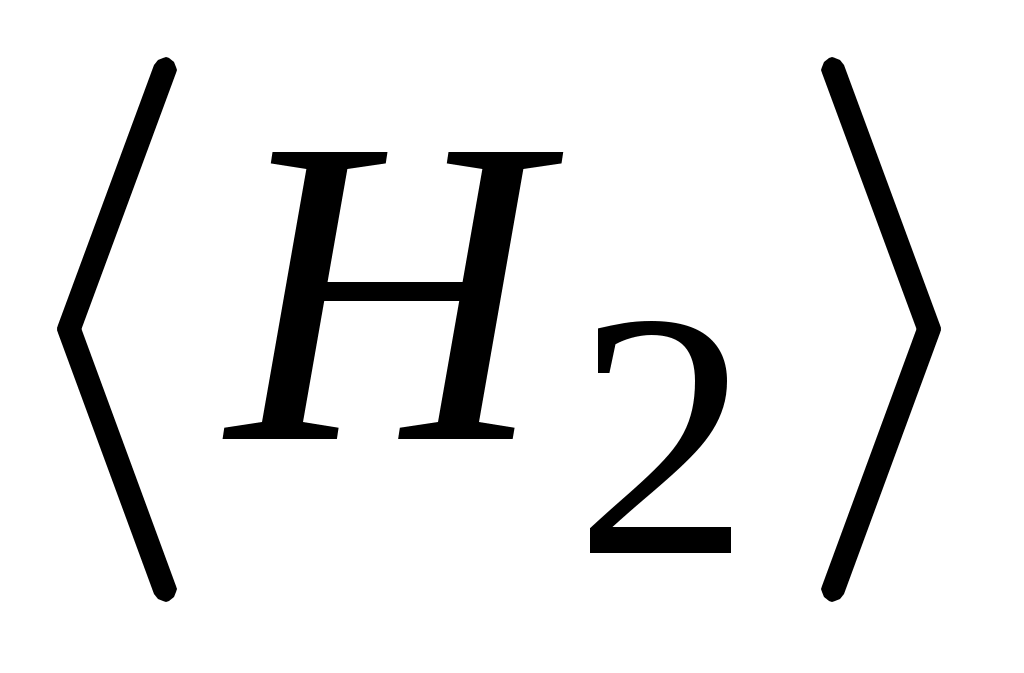 и среднеквадратичную погрешность
и среднеквадратичную погрешность 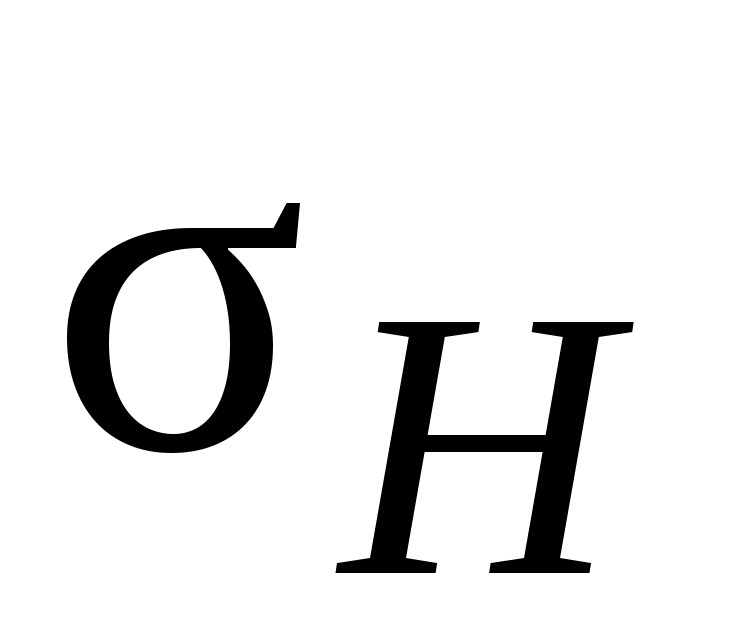 по формулам из введения.
по формулам из введения.
Таблица 5.1
| I, мА | 80 | 110 | 140 | 170 | 200 |
| | | | | | |
| | | | | | |
 | | | | | |
| | | | | | |
| | | ||||
| | | | | | |
| | | ||||