ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 161
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Проверка справедливости закона ома. определение удельного сопротивления провоЛОКИ
Цели работы:
-
проверить справедливость закона Ома; -
определить удельное сопротивление проволоки.
Приборы и принадлежности:
-
лабораторная установка, включающая в себя штатив с измерительной линейкой, амперметр и вольтметр; -
проволока из неизвестного материала.
Подготовка к работе
По лекциям и приведенному ниже списку литературы изучите следующие вопросы:
-
Электрический ток, сила и плотность тока. -
Электродвижущая сила (ЭДС), условные обозначения элементов электрической цепи. -
Разность потенциалов, напряжение. -
Закон Ома для однородного участка цепи, закон Ома в дифференциальной форме, сопротивление, удельное сопротивление, проводимость.
Вопросы для допуска к работе
-
Что называется электрическим током, силой и плотностью тока? -
Дайте определение ЭДС. В каких единицах она измеряется? Почему для поддержания стационарного электрического тока необходимо наличие источника ЭДС? -
Что называется разностью потенциалов, напряжением? В каких единицах они измеряются? -
Запишите закон Ома для однородного участка цепи, закон Ома в дифференциальной форме.
Теоретическое введение
Упорядоченное движение электрических зарядов называют электрическим током. В проводниках носители заряда перемещаются под действием приложенного электрического поля: положительные – по полю, отрицательные – против поля, то есть в проводниках возникает так называемый ток проводимости. Если упорядоченное движение электрических зарядов в пространстве происходит вместе с перемещением заряженных тел или частей тела, то возникают так называемые конвекционные токи.
Для возникновения и существования электрического тока необходимо наличие свободных носителей заряда (электронов, ионов и т. д.) и наличие электрического поля, которое бы приводило к направленному движению этих носителей. За направление тока условно принимают направление скорости движения положительных зарядов
Количественной мерой электрического тока является сила тока I – скалярная физическая величина, численно равная заряду, протекающему через поперечное сечение проводника в единицу времени. В общем случае сила тока есть производная от величины заряда по времени:
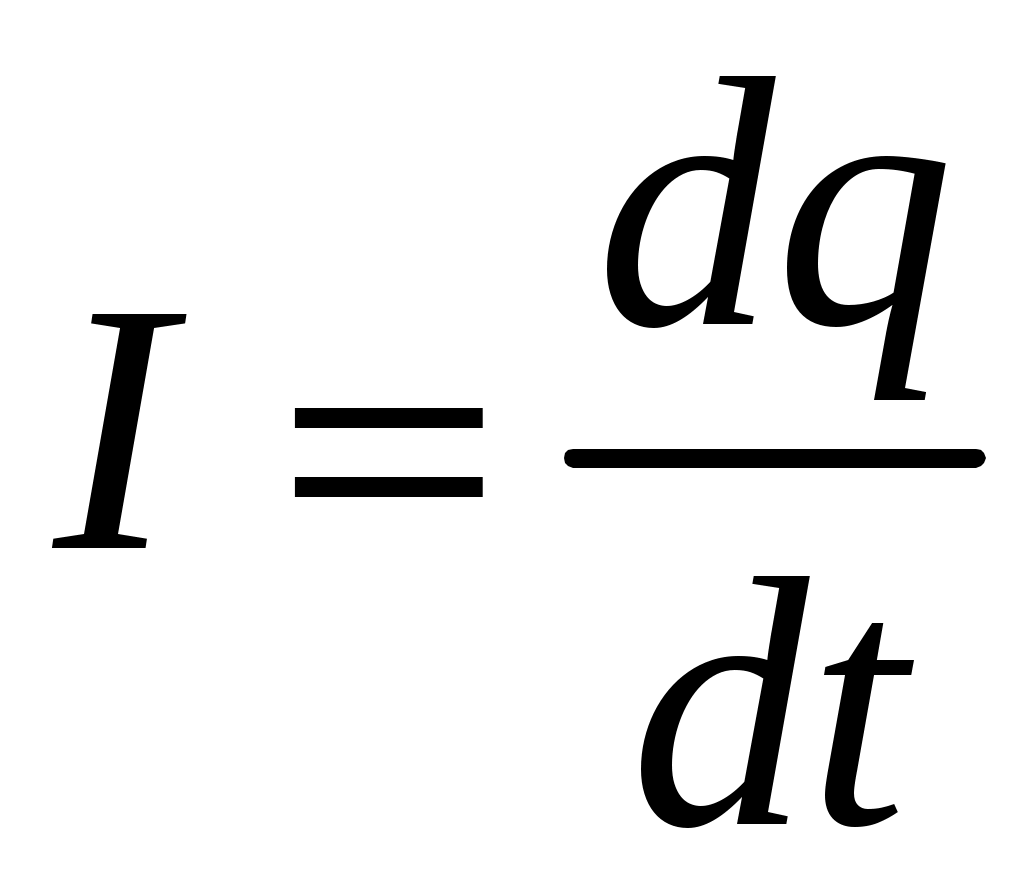 . (4.1)
. (4.1)Если сила тока и его направление не изменяются с течением времени, то такой ток называют постоянным. Для постоянного тока
где q – электрический заряд, протекающий через поперечное сечение проводника за время t.
Физическая величина, определяемая силой тока, протекающего через единицу площади поперечного сечения, перпендикулярного направлению тока, называется плотностью тока
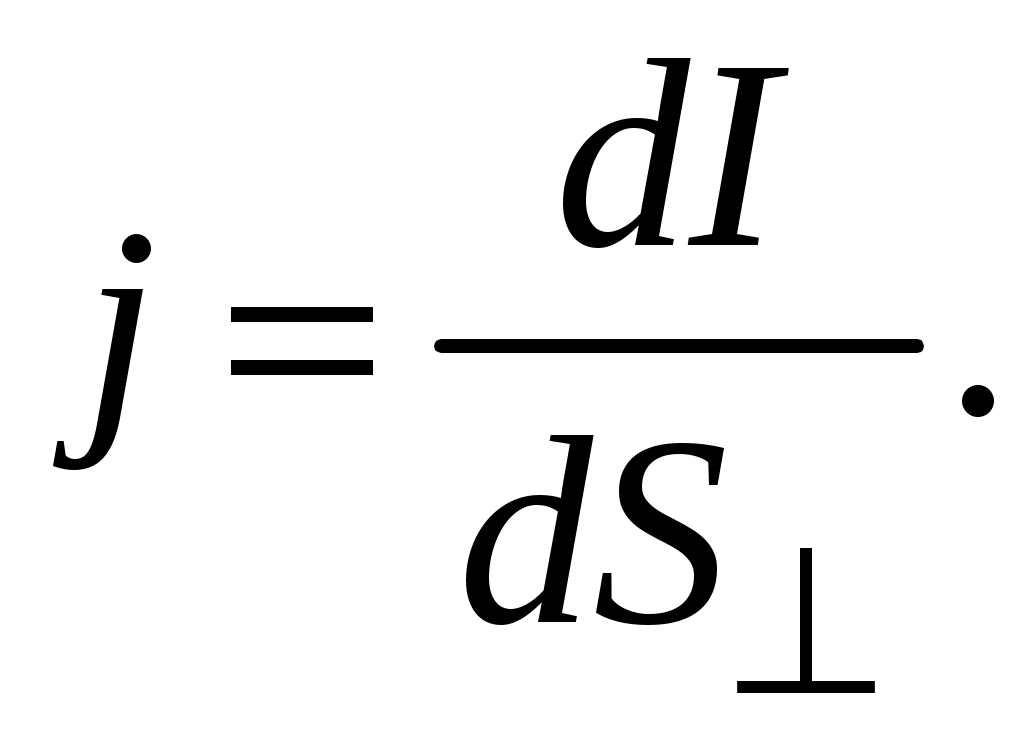 (4.3)
(4.3)Направление вектора плотности тока
где
Сила тока через произвольную поверхность
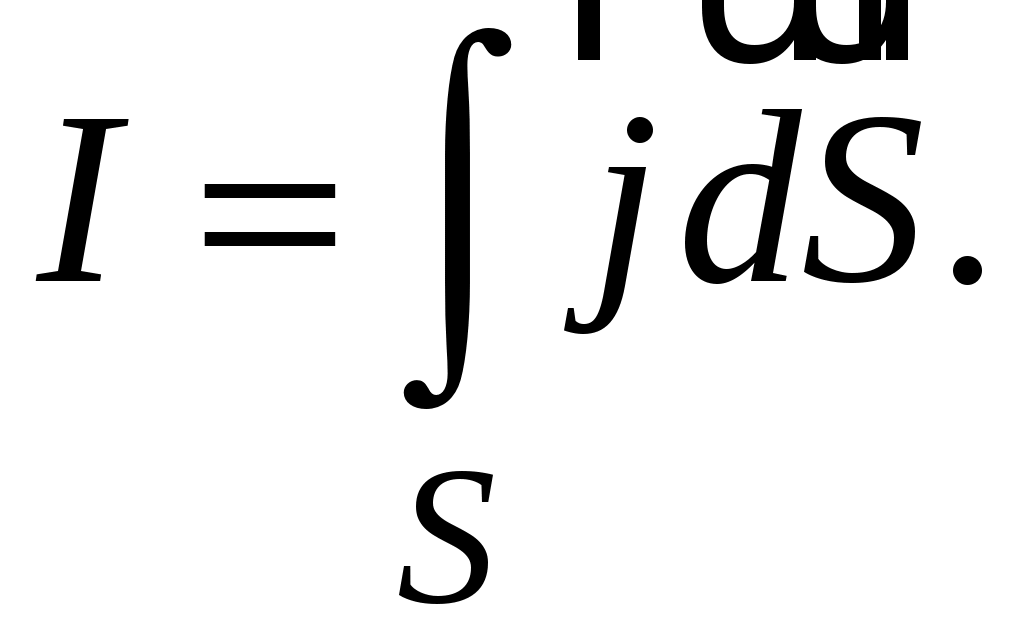 (4.5)
(4.5)Для поддержания тока в проводнике необходимо поддерживать разность потенциалов на концах проводника, для этого используют силы неэлектрической природы, их называют сторонними силами. Природа сторонних сил может быть различна: в гальванических элементах эти силы возникают за счет химической реакции между электродами и электролитами, в генераторах переменного тока – за счет механической энергии вращения ротора генератора. Под действием создаваемого поля сторонних сил электрические заряды внутри источника тока движутся в сторону, противоположную направлению электростатического поля, создавая необходимую разность потенциалов на концах проводника, присоединенного к этому источнику.
Величина, численно равная отношению работы сторонних сил к величине перемещаемого в единицу времени заряда, называется электродвижущей силой
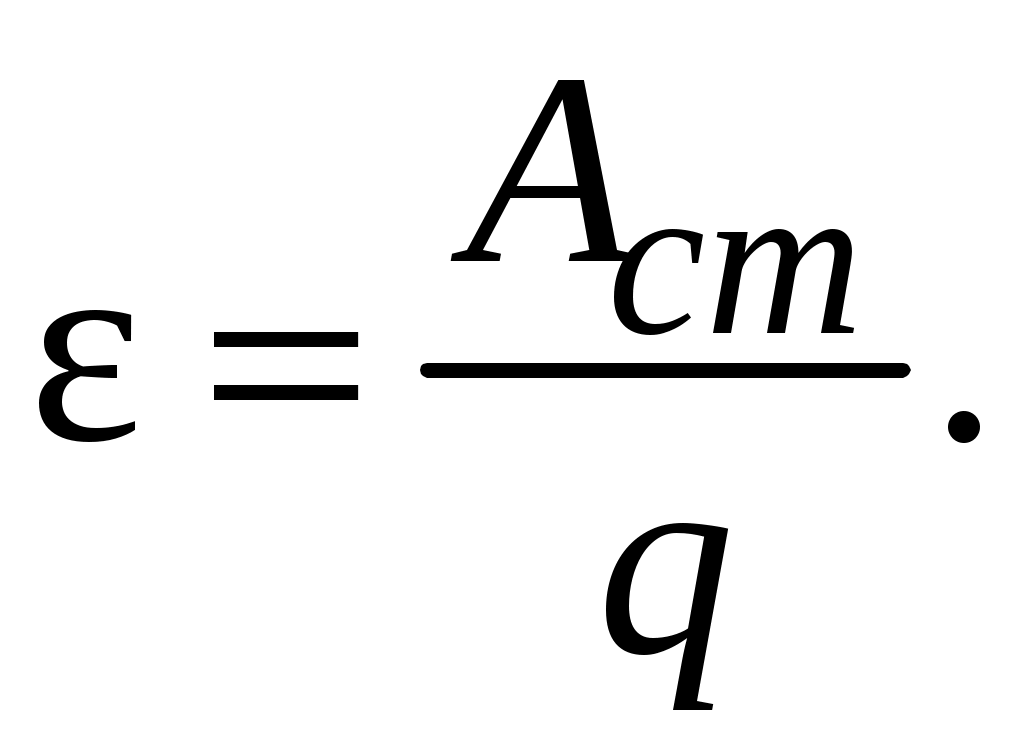 (4.6)
(4.6)Напряжением
Понятие «напряжение» является обобщенным понятием разности потенциалов: напряжение на концах проводника равно разности потенциалов в том случае, если нет сторонних сил
Немецкий физик Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника:
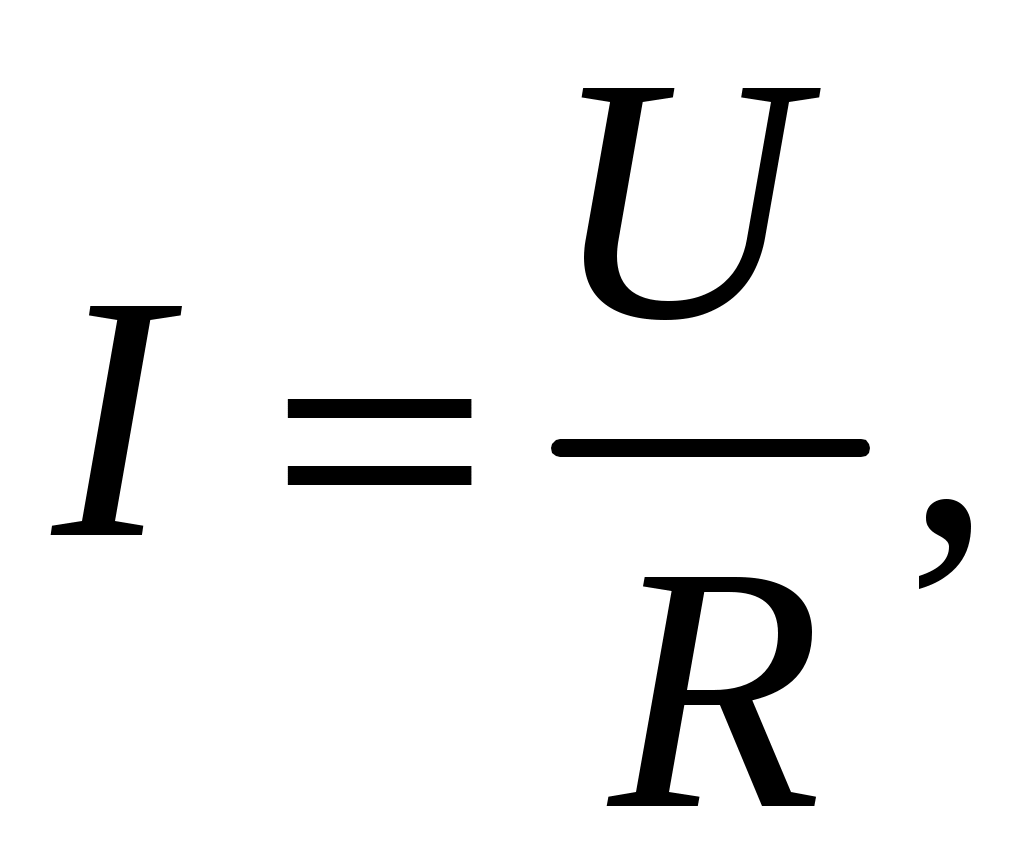 (4.7)
(4.7)где R – электрическое сопротивление проводника.
Уравнение (4.7) выражает закон Ома для однородного участка цепи.
Формально, сопротивление проводника R – это коэффициент пропорциональности между силой тока I в проводнике и напряжением Uна его концах. C физической точки зрения, сопротивление проводников обусловлено взаимодействием упорядоченно движущихся носителей заряда с кристаллической решеткой (в твердых проводниках) либо с хаотически движущимися молекулами среды (в жидкостях и газах).
Сопротивление проводников зависит от их размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника длины l и площади поперечного сечения S сопротивление равно:
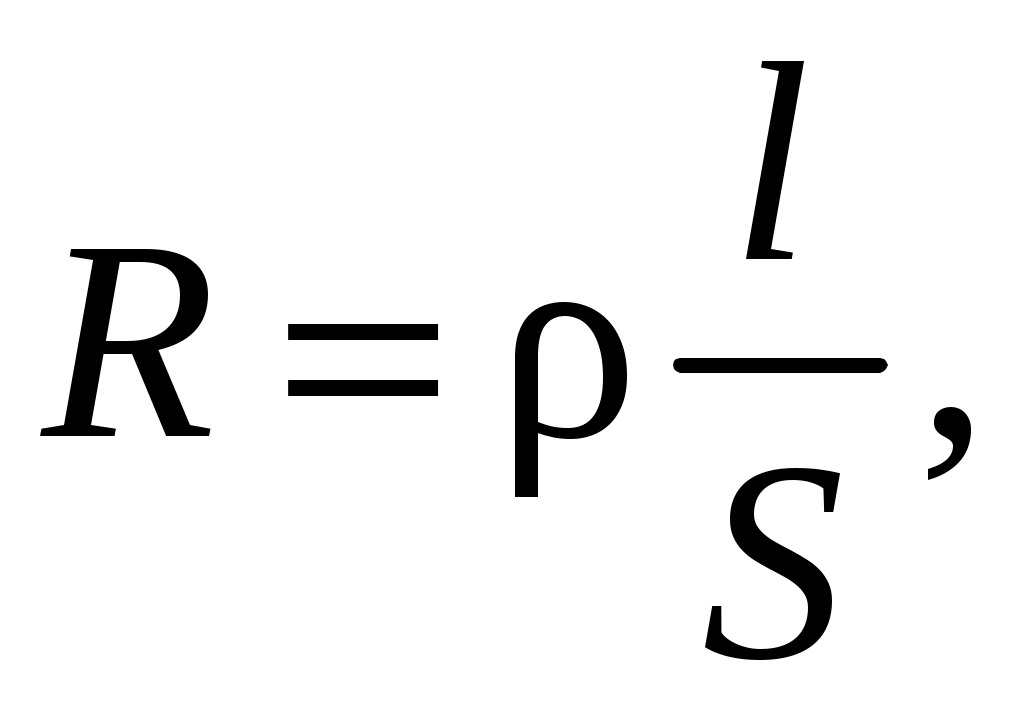 (4.8)
(4.8)где
Удельное сопротивление линейно зависит от температуры окружающей среды t:
где
– удельное сопротивление при температуре
Закон Ома в дифференциальной форме может быть получен на основании вышеизложенного материала, а также теории электростатического поля, изложенной в лабораторной работе № 21, в следующем виде:
где
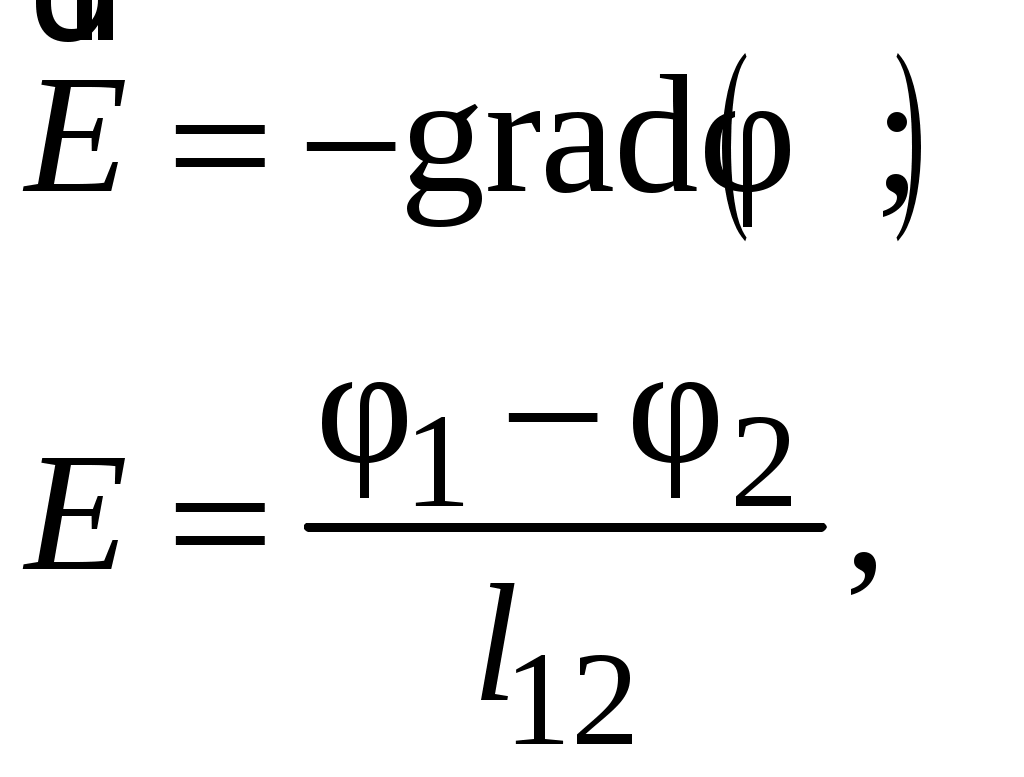 (4.10)
(4.10)где
Задание 1
Проверка влияния измерительных приборов на результаты измерений
Измерительные приборы вольтметр и амперметр должны включаться так, чтобы включение их в электрическую цепь как можно меньше влияло на результаты измерений. По этой причине внутреннее сопротивление вольтметра выбирается большим, а амперметра – минимальным. На рис. 4.1 показаны два разных способа включения амперметра и вольтметра в электрическую цепь.
Если переключатель находится в положении 1 (рис. 4.1, а), то миллиамперметр mА измеряет сумму токов, протекающих как по резистору R, так и по цепи вольтметра. Эти токи в случае, когда Rсоизмеримо по величине с внутренним сопротивлением вольтметра
а) б)
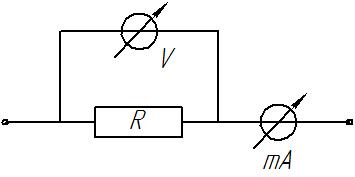
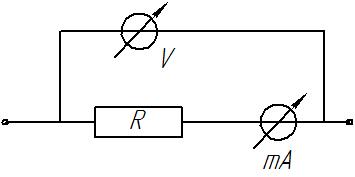
Рис. 4.1. Две схемы включения электроизмерительных приборов
Если же сопротивление Rмало и соизмеримо с внутренним сопротивлением миллиамперметра rmА, то и напряжения на резисторе Rи на миллиамперметре будут соизмеримы между собой. Следовательно, при включении по схеме (рис. 4.1, б) будут большие ошибки при измерении напряжения на сопротивлении, и вольтметр нужно включать по схеме (рис. 4.1, а) в положение 1 переключателя.
Чтобы сделать выбор в пользу первой или второй схемы, необходимо провести измерения зависимости напряжения от тока при первом и втором положениях переключателя. Схема, при которой показания вольтметра дают наименьшую разницу значений U, должна быть выбрана основной.
Задание 2
Проверка справедливости закона Ома для однородного участка цепи
Г. Ом установил свой закон на основе экспериментальных данных. Цель задания 2 повторить результаты Ома и экспериментально подтвердить справедливость формулы (4.7).
Если менять силу тока через проводники откладывать по координатным осям соответствующие значения силы тока I(х) и напряжения U(у), то экспериментальные точки должны располагаться вдоль прямой. Из-за случайных погрешностей экспериментальные точки могут отклоняться от прямой, поэтому прямая линия проводится так, чтобы отклонения всех точек от нее в среднем были минимальны (рис. 4.2).
Значение сопротивления проводника Rопределяется следующим образом. На проведенной прямой произвольным образом выбираем две точки 1, 2. Их абсциссы равны
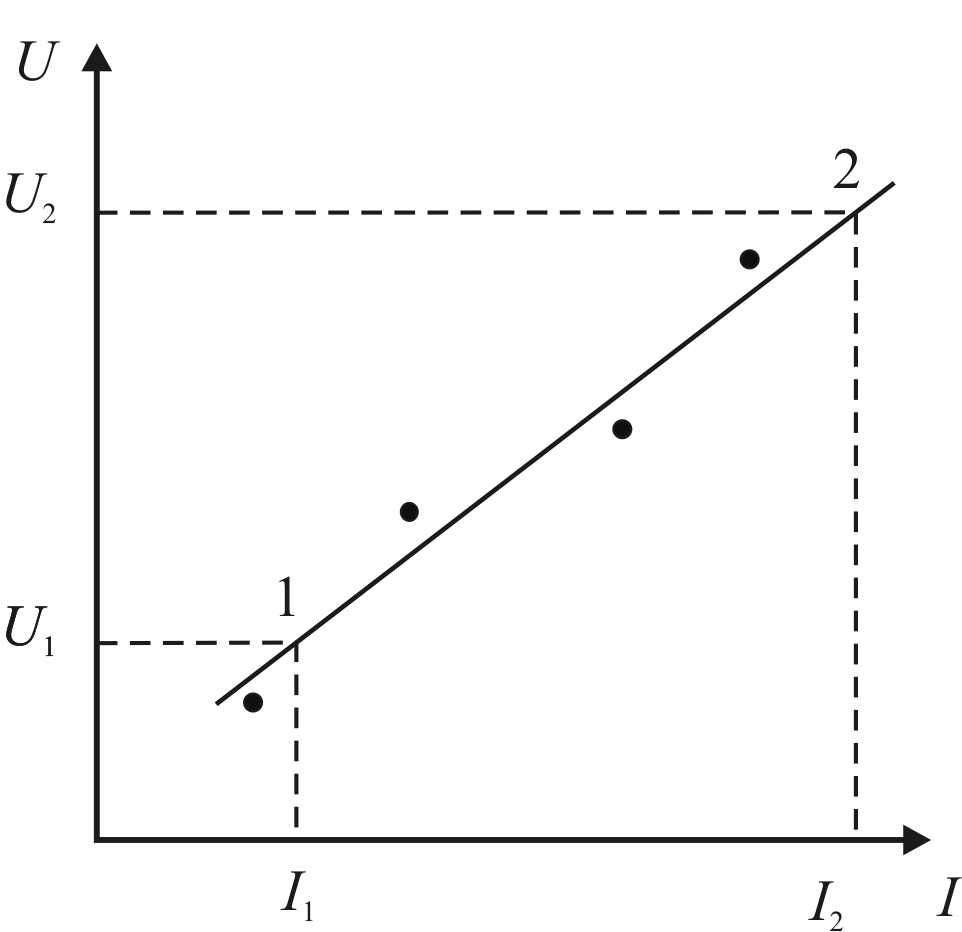
Рис 4.2. График зависимости напряжения на проводнике от силы тока
На основании формулы (4.7) имеем:
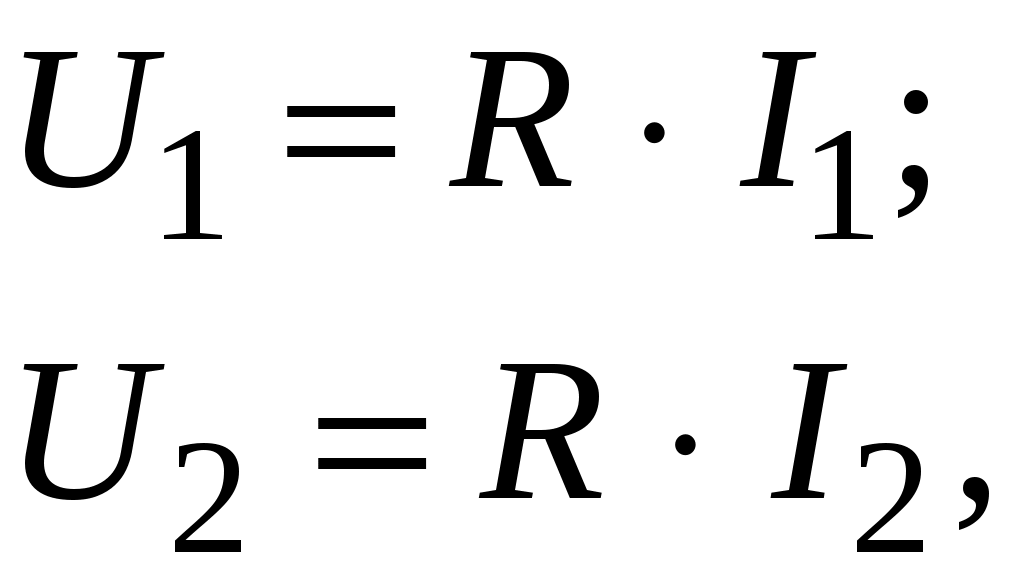 (4.11)
(4.11)Значение сопротивления