Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 147
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
как функцию от числа отрезков n. Так как
x a ih a bai.
i n
Точность вычисления определенного интеграла в зависимости от числа отрезков n найдем по формуле (3.13).

При
n 6
приближенное значение интеграла по формуле средних
прямоугольников равно 0.4968543017618265 с точностью 9.985166509519083*10^-4 .
Формула правых прямоугольников.
Запишем правую часть формулы правых прямоугольников (3.5)
как функцию от числа отрезков n.Так как
x a ih a bai.
i n
Определим точность вычисления интеграла по формуле (3.13):

При
n 69
приближенное значение интеграла по формуле правых
прямоугольников равно 0.4955340503706018 с точностью 9.982708115104377*10^-4.
Формула трапеций.
Запишем правую часть формулы трапеций (3.6) как функцию
от числа отрезков n.Так как
x a ih a bai.
i n
Точность вычисления определим по формуле (3.13) в зависимости от числа отрезков n.

При
n 5
приближенное значение интеграла по формуле
трапеций равно 0.4955661821417044
с точностью 9.580511825193483*10^-4.
Формула Симпсона.
Запишем правую часть формулы парабол (3.9) как функцию
от числа отрезков n.Так как
x a ih a bai.
i n
Найдем точность вычисления по формуле (3.13).

При
n 2
приближенное значение интеграла по формуле
парабол равно 0.4965270391248789 с точностью 4.725044233366837*10^-6.
ЗАДАНИЕ 2
b
Задача 1. Найти интеграл f(x)dxаналитически с помощью формулы Нью-
a
тона-Лейбница
Для данной функции f(x) = e^(2x)sin(3x) интеграл можно найти аналитически с помощью формулы Ньютона-Лейбница:
∫[a,b] f(x) dx = F(b) - F(a),
где F(x) - первообразная функции f(x).
Чтобы найти первообразную F(x), воспользуемся методом интегрирования по частям, подставив u = sin(3x), dv = e^(2x)dx, и получим:
∫ e^(2x)sin(3x) dx = (-1/3)e^(2x)cos(3x) + (2/9)e^(2x)sin(3x) + C,
где C - произвольная константа интегрирования.
Теперь можем вычислить значение определенного интеграла на отрезке [0.4, 1.2]:
∫[0.4;1.2] e^(2x)sin(3x) dx = F(1.2) - F(0.4)
= [(-1/3)e^(21.2)cos(31.2) + (2/9)e^(21.2)sin(31.2)] - [(-1/3)e^(20.4)cos(30.4) + (2/9)e^(20.4)sin(30.4)]
≈ -0.181.
Таким образом, аналитическое решение данного интеграла на отрезке [0.4, 1.2] равно примерно -0.181.
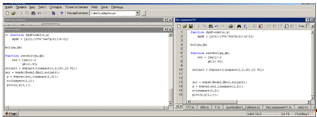
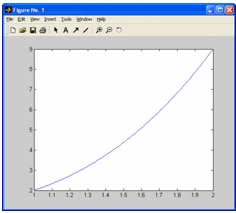
Задача 2. Найти неопределенный интеграл с помощью программы wxMaxima.
Для нахождения неопределенного интеграла e2x sin 3x на отрезке [0.4; 1.2] можно воспользоваться программой wxMaxima.
Введите следующий код:
integrate(exp(2*x)*sin(3*x), x);
(3*%e^(2*x)*sin(3*x))/13 - (2*%e^(2*x)*cos(3*x))/13
float(subst(x=1.2, %)-(subst(x=0.4,%)));
Результат выполнения будет
0.04931991336632227
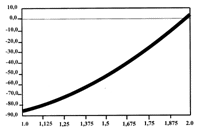
Таким образом, определенный интеграл функции e^(2x)*sin(3x) на отрезке [0.4, 1.2] равен примерно 0.0493.
| | f(x) | [a,b] | | f(x) | [a,b] |
| 1 | 1 tg2x 1 | [0.4; 0.8] | 21 | xarctg(2x) | [0,1; 0.3] |
| 2 | cos 3x (1 cos 3x)2 | [0.8; 1.6] | 22 | exsin 2x | [2; 2.4] |
| 3 | 1 x x3 4 | [0.18; 0.98] | 23 | ctg3x(cos 3x)2 | [1.2; 1.4] |
| 4 | sin x 1 sin x | [0.8; 1.6] | 24 | 3 x3 ln2 x | [1.2; 1.6] |
| 5 | arctg(1 x) | [0.1; 0.2] | 25 | arctg 2x1 | [0.6; 1.4] |
| 6 | x2 lg(x 2) | [0; 0.4] | 26 | (1 x)sin x | [1,4; 1.8] |
| 7 | x2arctg(x/ 3) | [0.8; 1.6] | 27 | cos x  1 cos x | [3.6;4] |
| 8 | e2x sin 3x | [0.4; 1.2] | 28 | 1 2x 2 ln 2x | [0.4; 1.4] |
| 9 | tg2x (sin 2x)2 | [0.8; 1.2] | 29 | (2x 3)cos x | [0.4; 0.6] |
| 10 | 4 x9 ln2 (4x) | [1.2; 1.4] | 30 | 1 x  2 x | [1.2; 1.6] |
| 11 | (2 x)sin x | [1; 1.5] | 31 | 2 x3 ln2 (2x) | [1.2; 1.4] |
| 12 | 5x xlg x | [0.2; 1] | 32 | x2 lg(2 x) | [1.4; 1.6] |
| 13 | (2x 3)sin x | [0.4; 1.2] | 33 | 3 x3 ln 3x | [0.4; 1] |
| 14 | 1 e x | [0.2; 0.6] | 34 | sin 2x  (2 3cos2 x)2 | [-1;0] |
| 15 | (2x 5) cos x | [0.4; 1.2] | 35 | 1 x4 x2 1 | [0.4; 0.6] |
| 16 | 1  1 x x2 | [0; 4] | 36 | x(2 lg x) | [1.2; 1.4] |
| 17 | arctg(1 x) | [0.7; 0.9] | 37 | arctg 3x1 | [0.4; 0.6] |
| 18 | 1 x  2 x | [0.4; 0.8] | 38 | 1 ex | [0.2; 0.6] |
| 19 | 1 ex | [1.4; 1.6] | 39 | 1  5 2x x2 | [-2.2; -1.2] |
| 20 | 1  sin4 x | [0.5;0.7] | 40 | (3x 5)cos x | [1, 1.4] |










| Задача 3. Вычислить определённый интеграл | с помощью | программы |
| wxMaxima. Для вычисления определенного интеграла ∫[a,b] e^(2x)sin(3x)dx с помощью программы wxMaxima, следует выполнить следующие шаги: Введите команду integrate(exp(2*x)*sin(3*x), x, 0.4, 1.2) в окно ввода команд. Нажмите Enter, Результатом выполнения команды будет значение определенного интеграла на заданном интервале: 0.14717267739138716 Таким образом, определенный интеграл ∫[0.4; 1.2] e^(2x)sin(3x)dx ≈ 0.1472. 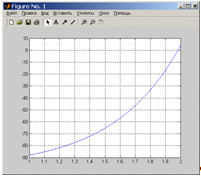 | | |
| Задача 4. Вычислить определённый интеграл | посредством | встроенной |
| функции приближенного вычисления quadpack. | | |
| from scipy.integrate import quad def integrand(x): return np.exp(2*x)*np.sin(3*x) result, error = quad(integrand, 0.4, 1.2) print("Значение определенного интеграла:", result) Значение определенного интеграла: 0.1471726773323859  Задача 5. Вычислить определённый интеграл | посредством | встроенной |
| функции приближенного вычисления romberg. | | |
import numpy as np
from scipy.integrate import romberg
def integrand(x):
return np.exp(2*x)*np.sin(3*x)
result = romberg(integrand, 0.4, 1.2)
print("Значение определенного интеграла:", result)
Значение определенного интеграла: 0.14717267733238297
Задача 6. Вычислить интеграл f(x)dxметодом левых прямоугольников.
a
b
import numpy as np
def integrand(x):
return np.exp(2*x)*np.sin(3*x)
a = 0.4 # нижний предел интегрирования
b = 1.2 # верхний предел интегрирования
n = 100 # количество разбиений
dx = (b - a) / n # шаг сетки
result = 0 # инициализациярезультата
for i in range(n):
result += integrand(a + i*dx) * dx
print("Значение интеграла:", result)
Значение интеграла: 0.14358859065483433
Задача 7. Вычислить интеграл f(x)dxметодом средних прямоугольников.
а
import numpy as np
def integrand(x):
return np.exp(2*x)*np.sin(3*x)
a = 0.4 # нижний предел интегрирования
b = 1.2 # верхний предел интегрирования
n = 100 # количество разбиений
dx = (b - a) / n # шаг сетки
result = 0 # инициализациярезультата
for i in range(n):
x1 = a + i*dx
x2 = a + (i+1)*dx
result += integrand((x1+x2)/2) * dx
print("Значение интеграла:", result)
Значение интеграла: 0.14717487289546777
b
Задача 8. Вычислить интеграл f(x)dxметодом правых прямоугольников.
а
import numpy as np
def integrand(x):
return np.exp(2*x)*np.sin(3*x)
a = 0.4 # нижний предел интегрирования
b = 1.2 # верхний предел интегрирования
n = 100 # количество разбиений
dx = (b - a) / n # шаг сетки
result = 0 # инициализациярезультата
for i in range(1, n+1):
result += integrand(a + i*dx) * dx