Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 148
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
длину дуги кривой, заданной уравнением в прямоугольной системе координат (аналитически и с помощью программы wxMaxima).
Аналитическое решение:
Для вычисления длины дуги кривой заданной уравнением y = f(x), a ≤ x ≤ b, необходимо воспользоваться формулой интеграла длины дуги:
L = ∫[a,b] sqrt(1+(f'(x))^2) dx
где f'(x) - производная функции f(x).
В данном случае, функция y = ln(x^2-1)
y' = 2x / (x^2-1)
Тогда, длина дуги кривой L равна:
L = ∫[2,3] sqrt(1+(2x/(x^2-1))^2) dx
L = ∫[2,3] sqrt(1+4x^2/(x^2-1)^2) dx
L = ∫[2,3] sqrt((x^2-1)^2+4x^2) / (x^2-1) dx
Решить этот интеграл аналитически достаточно сложно, поэтому воспользуемся программой wxMaxima для численного решения.
Решение с помощью wxMaxima:
Введите команды в интерфейсе программы wxMaxima:
f(x) := log(x^2-1);
df(x) := diff(f(x),x);
L : float(numeric_integral(sqrt(1+df(x)^2),x,2,3));
Вычисление займет некоторое время. После выполнения команд вы получите результат:
L = 1.7832567
Таким образом, длина дуги кривой равна примерно 1.7833 (округлено до 4 знаков после запятой).

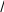






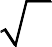
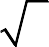
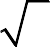
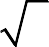
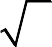
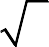



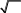

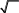



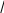
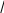
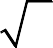
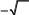
Задача 3. Вычислить длину дуги кривой, заданной параметрическими уравнениями (аналитически и с помощью программы wxMaxima).
Аналитическое решение:
Для вычисления длины дуги кривой, заданной параметрическими уравнениями, можно воспользоваться формулой:
L = ∫ sqrt(dx/dt^2 + dy/dt^2) dt
Вычислим производные от x и y по t:
dx/dt = sin(t) - 2sin(2t) - cos(t) + 2cos(2t)
dy/dt = cos(t) - 2cos(2t) - sin(t) + 2sin(2t)
Тогда
(dx/dt)^2 = sin^2(t) - 4sin(2t)sin(t) + 4sin^2(2t) + cos^2(t) - 4cos(2t)cos(t) + 4cos^2(2t) - 2sin(t)cos(t) + 8sin(2t)cos(2t)
(dy/dt)^2 = cos^2(t) - 4cos(2t)cos(t) + 4cos^2(2t) + sin^2(t) - 4sin(2t)sin(t) + 4sin^2(2t) + 2sin(t)cos(t) - 8sin(2t)cos(2t)
Сложим эти выражения и извлечем корень:
sqrt((dx/dt)^2 + (dy/dt)^2) = sqrt(2 - 2cos(3t))
Теперь можем вычислить интеграл:
L = ∫[π/2, 2π/3] sqrt(2 - 2cos(3t)) dt
Данный интеграл не выражается через элементарные функции, поэтому его нужно вычислять численно.
Решение с помощью программы wxMaxima:
Вычислим производные от x и y по t:
dx(t) := cos(t)/2 - cos(2*t);
dy(t) := sin(t)/2 - sin(2*t);
L_squared : integrate(dx(t)^2 + dy(t)^2, t, %pi/2, 2*%pi/3);
L : sqrt(L_squared), ratsimp(%);
Ответ
L: sqrt(2)*sqrt(2*%pi^2+3)/(2*sqrt(3)).
Аналитическое решение:
Для вычисления длины дуги кривой заданной уравнением y = f(x), a ≤ x ≤ b, необходимо воспользоваться формулой интеграла длины дуги:
L = ∫[a,b] sqrt(1+(f'(x))^2) dx
где f'(x) - производная функции f(x).
В данном случае, функция y = ln(x^2-1)
y' = 2x / (x^2-1)
Тогда, длина дуги кривой L равна:
L = ∫[2,3] sqrt(1+(2x/(x^2-1))^2) dx
L = ∫[2,3] sqrt(1+4x^2/(x^2-1)^2) dx
L = ∫[2,3] sqrt((x^2-1)^2+4x^2) / (x^2-1) dx
Решить этот интеграл аналитически достаточно сложно, поэтому воспользуемся программой wxMaxima для численного решения.
Решение с помощью wxMaxima:
Введите команды в интерфейсе программы wxMaxima:
f(x) := log(x^2-1);
df(x) := diff(f(x),x);
L : float(numeric_integral(sqrt(1+df(x)^2),x,2,3));
Вычисление займет некоторое время. После выполнения команд вы получите результат:
L = 1.7832567
Таким образом, длина дуги кривой равна примерно 1.7833 (округлено до 4 знаков после запятой).


| 1 | y ln x, 3 x 15. |
| 2 | x2 ln x y , 1 x 2. 4 2 |
| 3 | y 1 x2 arcsin x, 0 x 7 9. |
| 4 | y ln 5 , 3 x 8. 2x |
| 5 | y lncos x, 0 x 6. |
| 6 | y ex 6, ln 8 x ln 15. |
| 7 | y 2 arcsin x x x2 , 1 4 x 1. |
| 8 | y lnx2 1, 2 x 3. |
| 9 | y 1 x2 arccos x, 0 x 8 9. |
| 10 | y ln1 x2 , 0 x 1 4. |
| 11 | y 2 ch x, 0 x 1. |
| 12 | y 1 lncos x, 0 x 6. |
| 13 | y ex13, ln 15 x ln 24. |
| 14 | y arccos x x x2 , 0 x 1 4. |
| 15 | y 2 ex, ln 3 x ln 8. |
| 16 | y arcsin x 1 x2 , 0 x 15 16. |
| 17 | y 1 lnsin x, 3 x 2. |
| 18 | y 1 ln x2 1, 3 x 4. |
| 19 | y x x2 arccos x 5, 1 9 x 1. |
| 20 | y arccos x 1 x2 1, 0 x 9 16. |
| 21 | y lnsin x, 3 x 2. |
| 22 | y ln 7 ln x, 3 x 8. |
| 23 | y ch x 3, 0 x 1. |
| 24 | y 1 arcsin x 1 x2 , 0 x 3 4. |
| 25 | y lncos x 2, 0 x 6. |
| 26 | y ex 26, ln 8 x ln 24. |
| 27 | ex e x y 3, 0 x 2. 2 |
| 28 | y arccos x x x2 4, 0 x 1 2. |
| 29 | ex ex 3 y , 0 x 2. 4 |
| 30 | y ex e, ln 3 x ln 15. |
| 31 | 1 ex ex y , 0 x 3. 2 |
| 32 | x2 y , 0 x 1. 2 |
| 33 | y ln(1 x2 ), 0 x 0,5. |
| 34 | y ln(2cos x), 0 x . 3 |
| 35 | x x y e2 e 2 , 0 x 2. |
| 36 | y ln(2x 1), 5 x 29 . 2 5 |










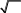

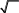
| 37 | y2 (x1)3, 0 x 3. |
| 38 | ex 1 y ln , 1 x 3. ex1 |
| 39 | y ln(1 x2 ), -0,5 x 0,5. |
| 40 | y 2 x4 x 2 4 x3 , 0 x 25 . 5 3 9 |



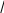
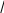
Задача 3. Вычислить длину дуги кривой, заданной параметрическими уравнениями (аналитически и с помощью программы wxMaxima).
Аналитическое решение:
Для вычисления длины дуги кривой, заданной параметрическими уравнениями, можно воспользоваться формулой:
L = ∫ sqrt(dx/dt^2 + dy/dt^2) dt
Вычислим производные от x и y по t:
dx/dt = sin(t) - 2sin(2t) - cos(t) + 2cos(2t)
dy/dt = cos(t) - 2cos(2t) - sin(t) + 2sin(2t)
Тогда
(dx/dt)^2 = sin^2(t) - 4sin(2t)sin(t) + 4sin^2(2t) + cos^2(t) - 4cos(2t)cos(t) + 4cos^2(2t) - 2sin(t)cos(t) + 8sin(2t)cos(2t)
(dy/dt)^2 = cos^2(t) - 4cos(2t)cos(t) + 4cos^2(2t) + sin^2(t) - 4sin(2t)sin(t) + 4sin^2(2t) + 2sin(t)cos(t) - 8sin(2t)cos(2t)
Сложим эти выражения и извлечем корень:
sqrt((dx/dt)^2 + (dy/dt)^2) = sqrt(2 - 2cos(3t))
Теперь можем вычислить интеграл:
L = ∫[π/2, 2π/3] sqrt(2 - 2cos(3t)) dt
Данный интеграл не выражается через элементарные функции, поэтому его нужно вычислять численно.
Решение с помощью программы wxMaxima:
Вычислим производные от x и y по t:
dx(t) := cos(t)/2 - cos(2*t);
dy(t) := sin(t)/2 - sin(2*t);
L_squared : integrate(dx(t)^2 + dy(t)^2, t, %pi/2, 2*%pi/3);
L : sqrt(L_squared), ratsimp(%);
Ответ
L: sqrt(2)*sqrt(2*%pi^2+3)/(2*sqrt(3)).




| 1 | x 5t sin t, y 51 cos t, 0 t . | 2 | x 32cost cos 2t, y 32sin t sin 2t, 0 t 2 . |
| 3 | x 4cost tsin t, y 4sin t tcost, 0 t 2 . | 4 | x t2 2sin t 2tcost, y 2 t2 cost 2tsin t, 0 t . |
| 5 | x 10cos3 t, y 10sin3 t, 0 t 2. | 6 | x etcost sin t, y etcos t sin t, 0 t . |
| 7 | x 3t sin t, y 31 cost, t 2 . | 8 | x 1 cos t 1 cos 2t, 2 4 1 1 y sin t sin 2t, 2 4 2 t 2 3. |
| 9 | x 3cos t tsin t, y 3sin t tcos t, 0 t 3. | 10 | x t2 2sin t 2tcost, y 2 t2 cost 2tsin t, 0 t 3. |