Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 152
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 1 2 2
1 4 1
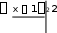
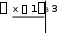 3 3
3 3
16 8

4
1
8 .

 3 3
3 31
Для решения подобных задач в Maxima следует выполнить следующиедействия:
-
Построить криволинейную трапецию. -
Найти точки пересечения кривых. -
Составить и вычислить определенный интеграл с помощью программы Maxima и вручную. -
Записать ответ.
Пример 10. Найти объем тела, образованного вращением фигуры,
ограниченной линиями
Oy.
y 1
x2 1
, ???? = 0, ???? = 0, ???? = 1 вокруг оси а) Ox, б)
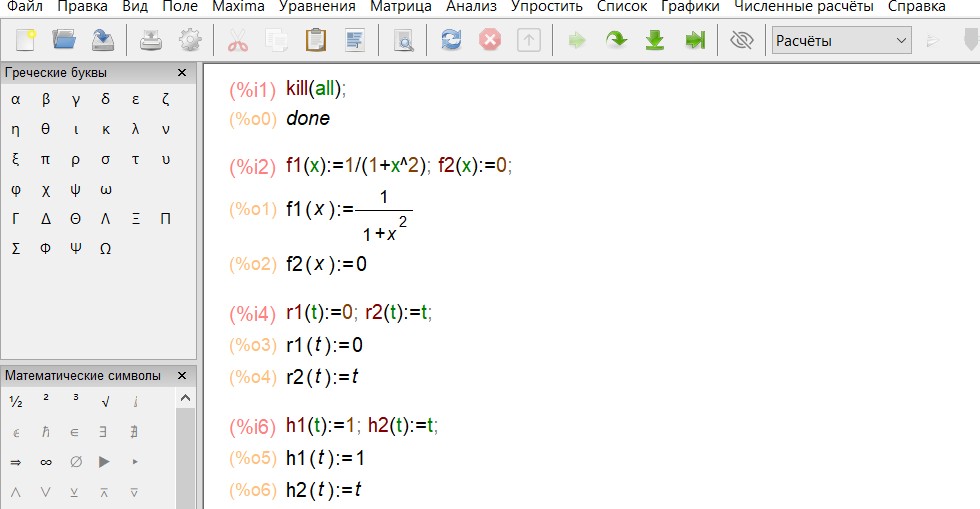
Построим график функций
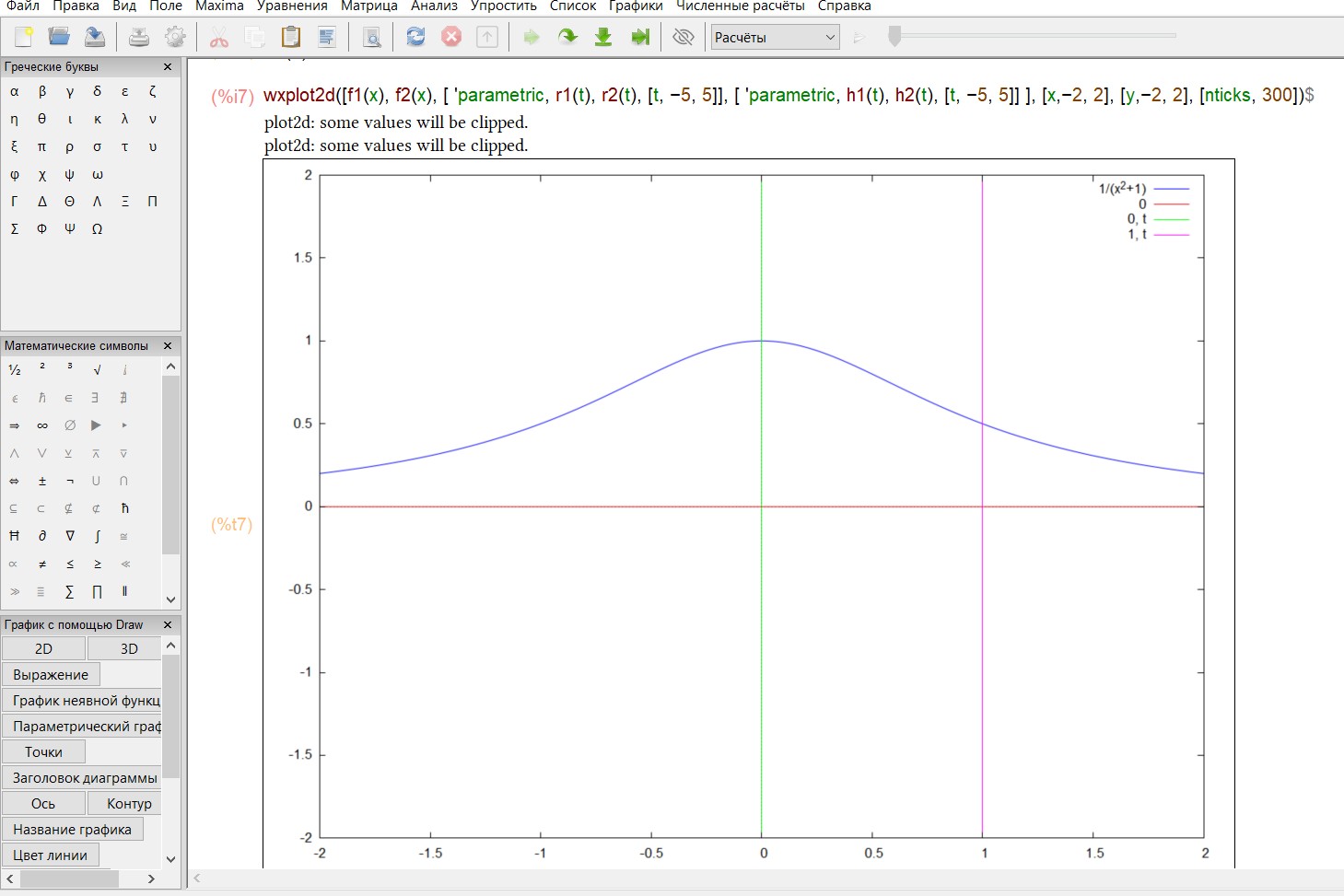
а) Если трапеция вращается вокруг оси Ox,тогда вычисляем интеграл:
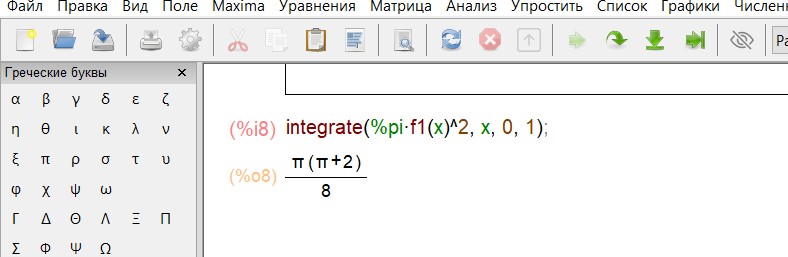
б) Если трапеция вращается вокруг оси Oy,тогда область нужно разделить на две подобласти:
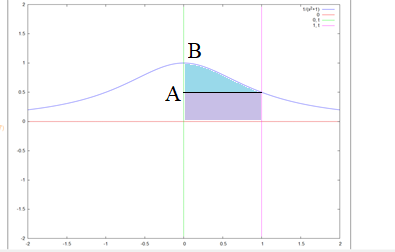
 Найдем ординаты точек Aи Bи вычислим объем тела вращения:
Найдем ординаты точек Aи Bи вычислим объем тела вращения: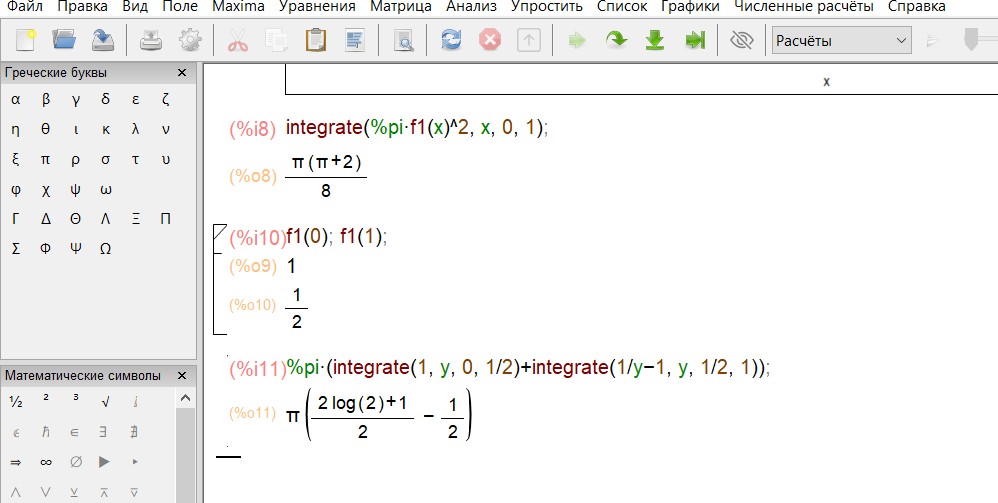
Задача 4. Вычислить объем тела
, образованного вращением фигуры, ограни- ченной графиками функций (аналитически и с помощью программы wxMax- ima).
Для того чтобы вычислить объем тела, образованного вращением фигуры вокруг оси x, мы можем использовать интеграл объема:
V = ∫[a,b] πy^2 dx
где [a,b] - интервал значений x, на котором определена фигура.
Используя графики функций y = 2x - x^2 и y = -x + 2, мы видим, что они пересекаются в точках (0, 2) и (1, 1). Также заметим, что функция y = 2x - x^2 является нижней границей фигуры, а функция y = -x + 2 - верхней границей.
Таким образом, интервал [a,b] для нашего интеграла равен [0,1].
Аналитический расчет:
Тогда объем тела можно вычислить следующим образом:
V = ∫[0,1] π(2x - x^2)^2 dx
= π∫[0,1] (4x^2 - 4x^3 + x^4) dx
= π[4/3x^3 - x^4 + 1/5x^5] от 0 до 1
= π(4/3 - 1 + 1/5)
= π(8/15)
Поэтому, объем тела, образованного вращением фигуры вокруг оси x, равен π(8/15).
Расчет с помощью программы wxMaxima:
Мы можем использовать интегральную функцию Maxima для вычисления этого интеграла:
V: integrate(pi*(2*x-x^2)^2,x,0,1);
Используя эту команду, мы получим ответ:
V: 8*%pi/15
Таким образом, объем тела, образованного вращением фигуры вокруг оси x, равен π(8/15), как и в аналитическом расчете.
| 1 | y x2 5x 6, y 0. |
| 2 | 2x x2 y 0, 2x2 4x y 0. |
| 3 | y 3sin x, y sin x, 0 x . |
| 4 | y 5cos x, y cos x, x 0, x 0. |
| 5 | y sin2 x, x 2, y 0. |
| 6 | x 3 y 2, x 1, y 1. |
| 7 | y xex, y 0, x 1. |
| 8 | y 2x x2, y x 2, x 0. |
| 9 | y 2x x2, y x 2. |
| 10 | y e1x, y 0, x 0, x 1. |
| 11 | y x2 , y2 x 0. |
| 12 | x2 y 22 1. |
| 13 | y 1 x2, x 0, x y 2, x 1. |
| 14 | y x2, y 1, x 2. |
| 15 | y x3, y x. |
| 16 | y sin x2, y x2. |
| 17 | x2 y , y 12 2x, x 0. 4 |
| 18 | y xex, y 0, x 1. |
| 19 | x2 x3 y , y . 2 8 |
| 20 | y xex, y 0, x 1. |
| 21 | y x1, y 0, y 1, x 0,5. |
| 22 | y ln x, x 2, y 0. |
| 23 | y x12 , y 1. |
| 24 | y2 x 2, y 0, y x3, y 1. |
| 25 | y x3, y x2. |
| 26 | y arccos x5, y arccos x3, y 0. |
| 27 | y arcsin x, y arccos x, y 0. |
| 28 | y x2 2x1, x 2, y 0. |
| 29 | y x3, y x. |
| 30 | y arccos x, y arcsin x, x 0. |







| 31 | y x12 , x 0, x 2, y 0. |
| 32 | y arccos x3, y arccos x, y 0. |
| 33 | y x2, x 2, y 0. |
| 34 | y x2 1, y x, x 0, y 0. |
| 35 | y arcsin x5, y arcsin x, y 2. |
| 36 | y x12 , y 1. |
| 37 | x2 x3 y , y . 2 8 |
| 38 | y x12 , x 1, x 2, y 0. |
| 39 | y 3 x, x=8, y 0. |
| 40 | x2 y , y 12 2x, y 0. 4 |