Файл: Министерство транспорта российской федерации федеральное государственное образовательное учреждение высшего профессионального образования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 161
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Фюзеляж же, напротив, сильно отличается по форме от рассмотренных выше частей самолета. Фюзеляж - это основная часть конструкции самолета, соединяющая в единое целое все его части и предназначенная для размещения экипажа, пассажиров, багажа, грузов и оборудования самолета. Формы фюзеляжей самолетов весьма разнообразны и выбираются исходя из стремления получить большой полезный объем при малом аэродинамическом сопротивлении и невысокой массе конструкции, а также для удовлетворения специальных технических требований (обеспечение перевозки крупногабаритных грузов, обеспечение комфорта пассажиров и т.п.). Следствием этих требований является вытянутая удобообтекаемая форма фюзеляжа при виде сбоку (см. рис. 16). Формы поперечных сечений фюзеляжа при этом могут сильно различаться (см. рис. 17). Однако на практике фюзеляж чаще всего имеет форму тела вращения. Перейдем к рассмотрению геометрических характеристик фюзеляжа.
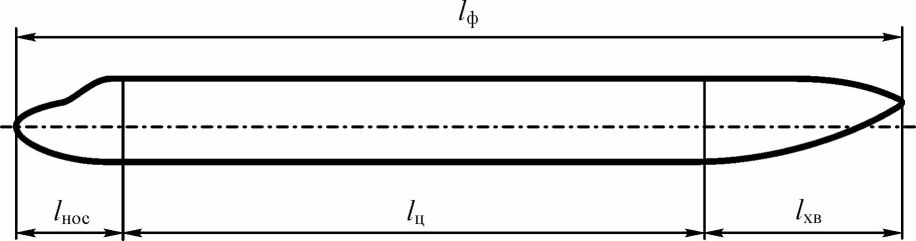

Рис. 17. Формы поперечных сечений фюзеляжа
Длина фюзеляжа /ф - наибольший размер фюзеляжа вдоль его продольной оси.
Площадь миделевого сечения фюзеляжа 5м.ф - наибольшая площадь поперечного сечения фюзеляжа плоскостью, перпендикулярной продольной оси фюзеляжа.
Максимальный эквивалентный диаметр фюзеляжа й?э.ф - диаметр условного круга, площадь которого равна площади миделевого сечения фюзеляжа:
1л с
7 Щ°м.ф
^э.ф — -»/ - (27)
V л
Удлинение фюзеляжа Хф - отношение длины фюзеляжа к его максимальному эквивалентному диаметру:
Хф=-У. (28)
и э.ф
Чаще всего у фюзеляжей можно выделить носовую, цилиндрическую (центральную) и хвостовую части и ввести для них соответствующие геометрические параметры. Удлинения этих частей фюзеляжа можно вычислить по следующим формулам:
л _ ^НОС л _ л _ Хв /эсл
^НОС — ? ^ХВ “ - \Г^)
^э.ф ^э.ф ^э.ф
Нетрудно заметить, что поскольку /ф = /нос + X + Хи, то:
Хф Хнос + Хц + Хув . (30)
-
Системы координат
При аэродинамических расчетах и изучении динамики движения самолетов используются различные системы координат. Чаще всего используются связанная, скоростная, нормальная и траекторная системы координат.
Связанная система координат 0XYZ жестко связана с самолетом (отсюда ее название). Начало этой системы совпадает с центром масс самолета (см. рис. 18). Ось ОХ лежит в базовой плоскости самолета, она направлена в сторону носовой части и, как правило, параллельна САХ. Эта ось называется продольной осью. Ось ОУ тоже лежит в базовой плоскости самолета, при этом она перпендикулярна оси ОХ и направлена к верхней части самолета. Она называется нормальной осью. Ось 0Z пер-
пендикулярна базовой плоскости самолета и направлена в сторону правого полукрыла. Эта ось называется поперечной осью.
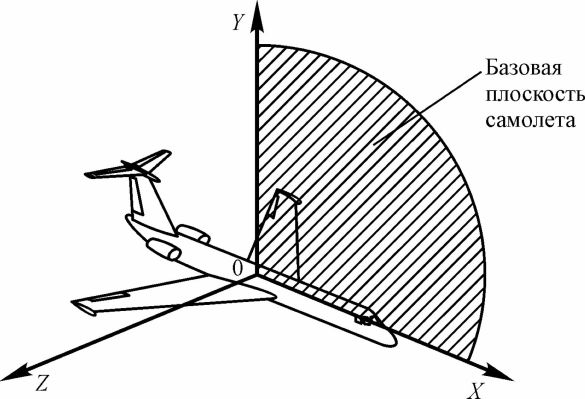
Рис. 18. Связанная система координат
Скоростная система координат 0XaYaZa связана с вектором скорости движения центра масс самолета относительно воздушной среды V (см. рис. 19), ее начало также помещают в центре масс самолета. Ось ОХа в скоростной системе координат всегда совпадает с вектором скорости и называется скоростной осью. Ось 0Ya перпендикулярна вектору скорости, лежит в базовой плоскости самолета и направлена к верхней части самолета. Она называется осью подъемной силы. Ось 0Za проводят так, чтобы она дополняла оси 0Ха и 0Ya до правой системы координат. Эта ось называется боковой осью.
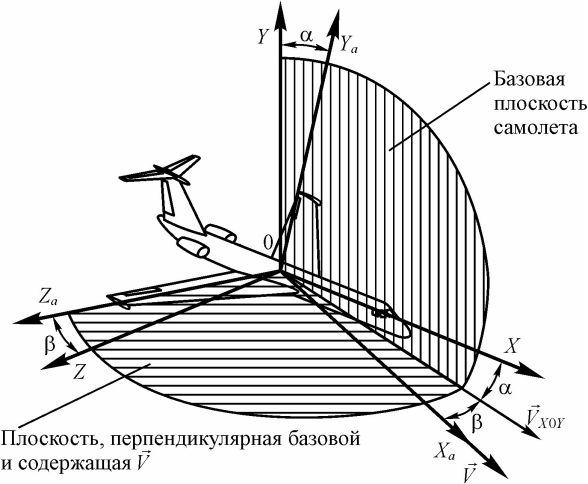
Для описания взаимного положения осей связанной и скоростной систем координат используются угол атака и угол скольжения. Углом атаки ос называется угол между осью ОХ связанной системы координат и проекцией вектора скорости V на базовую плоскость самолета - VXoг • Углом скольжения Р называется угол между вектором скорости V и базовой плоскостью самолета. Легко заметить, что если скольжение отсутствует (Р = 0), то определение угла атаки упрощается: угол ос будет равен углу между продольной осью ОХ и вектором скорости V.
Нормальная система координат 0XgYgZg используется для описания пространственного положения самолета относительно поверхности Земли. Начало координат этой системы совпадает с началом связанной системы координат (см. рис. 20). Ось 0Yg всегда направлена вверх по местной вертикали, а направление осей 0Xg и 0Zg выбирается в соответствии с решаемой задачей, при этом плоскость Xg0Zg всегда расположена горизонтально. Угол между осью 0Xg и проекцией оси ОХ на горизонтальную плоскость XXgOzg называется углом рыскания и обозначается \\1. Угол между продольной осью ОХ и горизонтальной плоскостью Xg0Zg называется углом тангажа и обозначается ср. Угол между поперечной осью 0Z и горизонтальной плоскостью Xg0Zg называется углом крена и обозначается у.
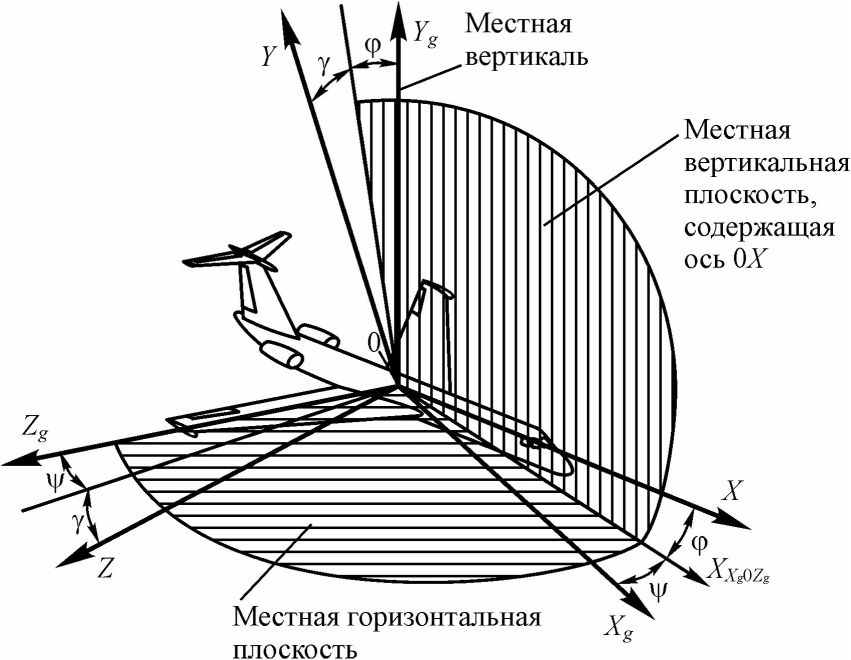
Рис. 20. Нормальная система координат
Траекторная система координат 0XKTKZK используется главным образом в динамике полета для описания движения самолета относительно поверхности Земли. В общем случае скорость полета относительно воздушной среды может не совпадать со скоростью полета относительно Земли, т.к. в реальной атмосфере почти всегда имеется движение воздушных масс, проще говоря, ветер. Ветер оказывает воздействие на самолет, и суммарная скорость его движения относительно поверхности Земли Ик (земная скорость) будет равна:
Ик =V + W, (31)
где V - скорость самолета относительно воздушной среды;
W - скорость ветра относительно Земли.
Траекторная система координат связана с вектором земной скорости Ик. Начало координат этой системы совпадает с началом связанной системы координат (см. рис. 21). Ось 0Хк совпадает с направлением вектора земной скорости Ик. Ось 0Ук размещается в вертикальной плоскости, проходящей через ось 0Хк, и направлена вверх от Земли. Ось 0ZK образует правую систему координат. Траекторная система координат может быть получена из нормальной путем поворота последней на угол пути и угол наклона траектории 0.
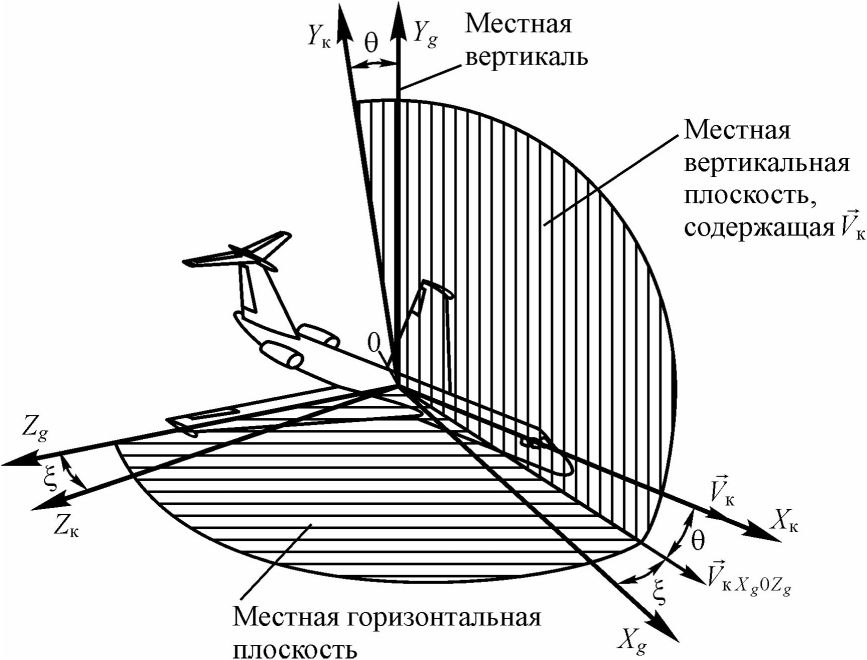
Рис. 21. Траекторная система координат
Углом пути называется угол между проекцией вектора Ик на горизонтальную плоскость XgQZg и осью 0Xg. Угол наклона траектории 0 - это угол между вектором земной скорости VK и местной горизонтальной плоскостью XgQZg.
-
Аэродинамические силы и моменты, действующие на самолет
Механическое воздействие набегающего потока на самолет сводится к нагрузкам, непрерывно распределенным по его поверхности. Для удобства изучения эти распределенные нагрузки приводят к результирующей силе, приложенной в центре масс самолета, которая называется аэродинамической силой и обозначается (см. рис. 22), а также моменту вокруг центра масс, который называется аэродинамическим моментом и обозначается М.
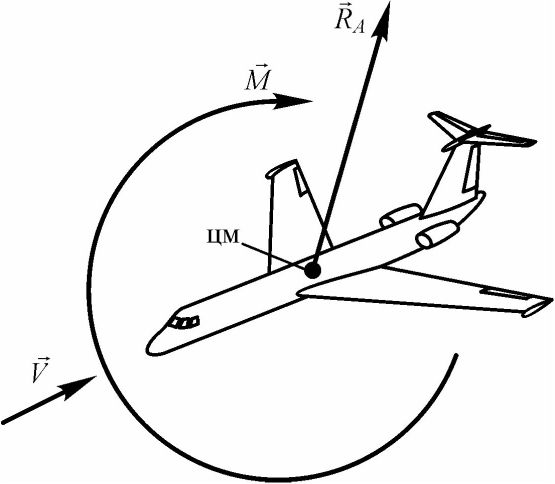
Рис. 22. Аэродинамическая сила и аэродинамический момент, действующие на самолет при его обтекании набегающим потоком
Теоретические и экспериментальные исследования показали, что величина аэродинамической силы прямопропорциональна скоростному напору рК2 набегающего потока и характерной площади обтекаемого тела S'.
pV2
Ra=Cr^-S, (32)
где Cr - коэффициент пропорциональности, который носит название коэффициента аэродинамической силы.
Аэродинамический момент также прямопропорционален скоростному рИ2
напору , характерной площади S и характерному линейному размеру об
текаемого тела Г.
рИ2
М = I, (33)
где m - коэффициент пропорциональности, который называется коэффициентом аэродинамического момента.
За характерную площадь и характерный размер берутся соответственно площади и размеры тех частей самолета, которые вносят основную долю в создание рассчитываемой силы или момента.
Разложим аэродинамическую силу Ra на составляющие по осям связанной и скоростной систем координат. В связанной системе координат эти проекции обозначаются и называются следующим образом:
X - аэродинамическая продольная сила;
Y - аэродинамическая нормальная сила;
Z - аэродинамическая поперечная сила.
В скоростной системе координат:
Ха - сила лобового сопротивления;
Ya - аэродинамическая подъемная сила;
Za - аэродинамическая боковая сила.
На рис. 23 показаны проекции аэродинамической силы Ra на оси связанной и скоростной систем координат при отсутствии скольжения.
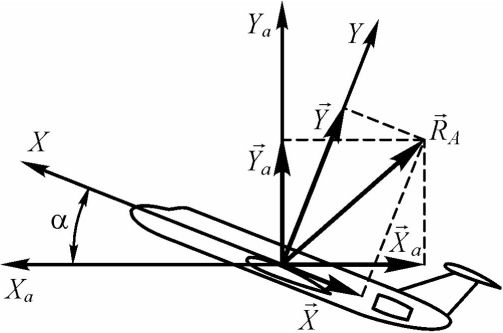
Рис. 23. Разложение аэродинамической силы по осям связанной и скоростной систем координат при Р = О
В дальнейшем мы будем иметь дело в основном с проекциями аэродинамической силы на оси скоростной системы координат. Воспользовавшись формулой (32), запишем выражения для этих проекций. При этом в качестве
характерной будем брать характерную площадь того элемента, который играет основную роль в создании данной силы.
Так, сила лобового сопротивления самолета складывается из сил лобового сопротивления фюзеляжа, крыла, оперения и других частей самолета. За характерную площадь можно принять площадь миделевого сечения фюзеля- жа ^м.ф-

(34)
pV2
у —Г нq
а ^ха °м.ф ->
где Сха - коэффициент лобового сопротивления.
В создании подъемной силы самолета основную роль играет крыло, поэтому в качестве характерной берется площадь крыла S^:

(35)
pV2
у — С нQ
1 а уа °кр 5
где Суа - коэффициент подъемной силы.
Аэродинамическая боковая сила в основном определяется вертикальным оперением и фюзеляжем, значительно меньший вклад в создание этой силы вносят крыло, горизонтальное оперение и другие части самолета. Поскольку вертикальное оперение является основным элементом при создании боковой силы (оно для этого предназначено), то его площадь SB 0 и принимают за характерную:

(36)
, рУ2 <,
za ^в.о?
где Cza - коэффициент боковой силы.
Так как аэродинамические моменты, действующие на самолет, рассчитываются в основном относительно связанных осей координат, найдем проекции момента М на оси связанной системы координат (см. рис. 24).
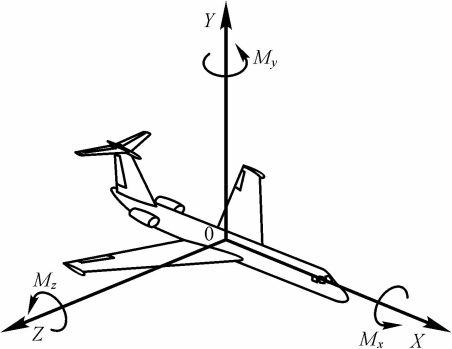
Аэродинамический момент относительно оси ОХ называется моментом крена. Он определяется в основном силами, действующими на крыло самолета и в меньшей степени - на вертикальное и горизонтальное оперения:
рИ2
(37) где тх - коэффициент момента крена.
Аэродинамический момент относительно оси ОУ называется моментом рыскания. Он создается силами, действующими в основном на вертикальное оперение и фюзеляж. Этот момент вычисляется по следующей формуле:
рИ2
M* = myX^-S в.о£в.о, (38)
где mv - коэффициент момента рыскания;
£в.о - плечо вертикального оперения (расстояние от точки приложения аэродинамической силы, возникающей на вертикальном оперении, до центра масс самолета).
Аэродинамический момент относительно оси 0 Z называется моментом тангажа. Он создается силами, действующими на крыло, горизонтальное оперение и фюзеляж. Вертикальное оперение практически не участвует в создании момента тангажа. Момент тангажа вычисляют по формуле:
рИ2
Mz = mz —, (39)
где mz - коэффициент момента тангажа.
-
Подъемная сила
Рассмотрим обтекание двояковыпуклого симметричного профиля идеальным газом (см. рис. 25). Профиль считается симметричным, если он симметричен относительно хорды. Пусть он сначала установлен под углом атаки ос = 0. В данном случае угол атаки равен углу между вектором скорости набегающего потока V и хордой профиля.
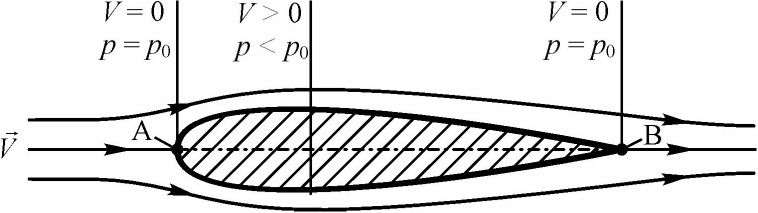
Рис. 25. Обтекание симметричного профиля при ос = О (без образования подъемной силы)
У носка профиля в передней критической точке А происходит полное торможение потока, статическое давление в этой точке максимально и равно полному давлению. Далее поток разделяется на два: один обтекает верхнюю поверхность профиля, другой - нижнюю. У задней кромки профиля потоки опять сливаются в задней критической точке В. В точке В также как и в точке А скорость потока равна 0, потому что здесь сходятся линии тока, идущие по верхней и нижней поверхностям профиля, а частица газа не может одновременно двигаться по двум направлениям. Следовательно, в точке В статическое давление также как и в точке А максимально и равно полному давлению. Но между точками А и В статическое давление отличается от полного давления. Это является следствием того, что в процессе движения от точки А к точке В площади поперечных сечений струек сначала уменьшаются, а потом растут. При этом в соответствии с уравнением неразрывности (10) скорость в струйках будет соответственно сначала расти, а затем падать. Из закона сохранения энергии в аэродинамике (см. уравнение Бернулли (16)) следует, что при увеличении скорости статическое давление уменьшается. Значит, от точки А до точки В на верхней и нижней поверхностях профиля будут располагаться зоны относительного разрежения. Поскольку мы рассматриваем симметричный профиль, то величины падения статического давления в этих зонах будут одинаковыми. Это значит, что в направлении, перпендикулярном вектору скорости набегающего потока, на профиль не будет воздействовать составляющая аэродинамической силы, названная выше подъемной.
Очевидно, что для того, чтобы получить подъемную силу нужно сделать профиль несимметричным или установить симметричный профиль под некоторым углом атаки ос ф 0 (см. рис. 26).
Рассмотрим обтекание профиля потоком под углом атаки ос > 0. В этом случае струйка, обтекающая профиль сверху будет иметь большее сужение,
чем струйка, обтекающая профиль снизу, а значит скорость в верхней струйке будет больше, чем в нижней (VB > VH). Это приведет к тому, что на верхней поверхности профиля статическое давление будет меньше, чем на нижней (ръ < /?„). Из-за этой разности образуется аэродинамическая подъемная сила, направленная вверх.
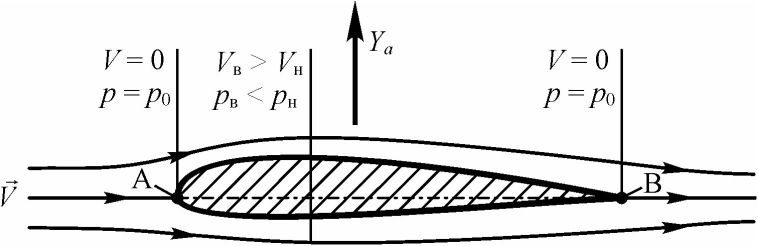
а) обтекание несимметричного профиля при ос = О
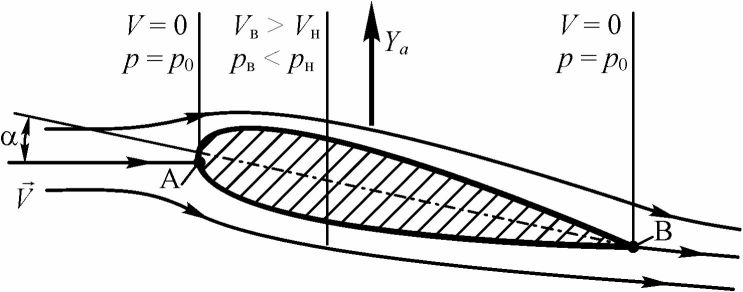
б) обтекание симметричного профиля при ос > О
Рис. 26. Обтекание профилей с образованием подъемной силы
Естественно предположить, что чем больше угол атаки или вогнутость профиля, тем больше будет и подъемная сила. Рассмотрим вначале влияние угла атаки на подъемную силу симметричного профиля. В формуле подъемной силы (35) имеется коэффициент, который зависит от угла атаки - это коэффициент подъемной силы Cva. График зависимости Cva от ос для симметричного и несимметричного профилей представлен на рис. 27, из которого видно, что при малых углах атаки коэффициент подъемной силы зависит от ос линейно.
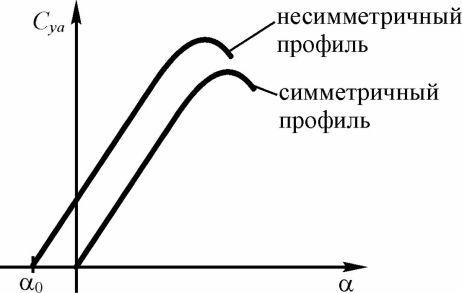
Рис. 27. Зависимость коэффициента подъемной силы от угла атаки
Если профиль имеет положительную относительную вогнутость, то кривая Cva = /(ос) смещается плоскопараллельно вверх. Угол атаки, при котором Суа = О обозначается ОСО, в данном случае осо< 0. Легко видеть, что при одном и том же угле атаки профиль, имеющий большую относительную вогнутость, будет иметь больший коэффициент подъемной силы.
На больших углах атаки нарушается плавное обтекание профиля. Это происходит из-за влияния вязкости на движение частиц в пограничном слое. В процессе движения вдоль верхней поверхности профиля частицы воздуха будут терять скорость. На каком-то этапе им не хватит кинетической энергии, чтобы двигаться дальше вдоль поверхности. В итоге на некотором участке верхней поверхности профиля произойдет отрыв пограничного слоя. Это явление приводит к нарушению линейности зависимости Cva = /(ос). При увеличении угла атаки зона отрыва также будет увеличиваться, но коэффициент подъемной силы Суа при этом продолжает расти и достигает своего максимального значения С/тах. Угол атаки, который соответствует Суатах, называется критическим углом атаки оскр (см. рис. 28). Величина критического угла атаки, как правило, не превышает 20°. При дальнейшем увеличении угла атаки отрыв потока достигнет интенсивности, при которой коэффициент подъемной силы будет резко падать.
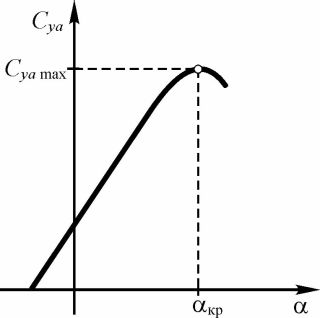
Рис. 28. Соответствие максимального значения коэффициента подъемной силы критическому углу атаки
-
Сила лобового сопротивления
Выше мы отметили, что сила лобового сопротивления складывается из сил, действующих на все части самолета, обтекаемые потоком. Но для упрощения и сокращения объема излагаемого материала рассмотрим только силу лобового сопротивления, возникающую на крыле самолета. Соответственно в качестве характерной площади будем использовать площадь крыла.
Сила лобового сопротивления крыла складывается из сил различной природы. В общем случае силу лобового сопротивления можно представить в виде следующей суммы:
Ха= X а тр + X а д + X а j + X а вл (40)
где Хатр - сила сопротивления трения;
Хал - сила сопротивления давления;
Xai - сила индуктивного сопротивления;
1 2 3 4 5 6

Рис. 21. Траекторная система координат
Углом пути называется угол между проекцией вектора Ик на горизонтальную плоскость XgQZg и осью 0Xg. Угол наклона траектории 0 - это угол между вектором земной скорости VK и местной горизонтальной плоскостью XgQZg.
-
Аэродинамические силы и моменты, действующие на самолет
Механическое воздействие набегающего потока на самолет сводится к нагрузкам, непрерывно распределенным по его поверхности. Для удобства изучения эти распределенные нагрузки приводят к результирующей силе, приложенной в центре масс самолета, которая называется аэродинамической силой и обозначается (см. рис. 22), а также моменту вокруг центра масс, который называется аэродинамическим моментом и обозначается М.

Рис. 22. Аэродинамическая сила и аэродинамический момент, действующие на самолет при его обтекании набегающим потоком
Теоретические и экспериментальные исследования показали, что величина аэродинамической силы прямопропорциональна скоростному напору рК2 набегающего потока и характерной площади обтекаемого тела S'.
pV2
Ra=Cr^-S, (32)
где Cr - коэффициент пропорциональности, который носит название коэффициента аэродинамической силы.
Аэродинамический момент также прямопропорционален скоростному рИ2
напору , характерной площади S и характерному линейному размеру об
текаемого тела Г.
рИ2
М = I, (33)
где m - коэффициент пропорциональности, который называется коэффициентом аэродинамического момента.
За характерную площадь и характерный размер берутся соответственно площади и размеры тех частей самолета, которые вносят основную долю в создание рассчитываемой силы или момента.
Разложим аэродинамическую силу Ra на составляющие по осям связанной и скоростной систем координат. В связанной системе координат эти проекции обозначаются и называются следующим образом:
X - аэродинамическая продольная сила;
Y - аэродинамическая нормальная сила;
Z - аэродинамическая поперечная сила.
В скоростной системе координат:
Ха - сила лобового сопротивления;
Ya - аэродинамическая подъемная сила;
Za - аэродинамическая боковая сила.
На рис. 23 показаны проекции аэродинамической силы Ra на оси связанной и скоростной систем координат при отсутствии скольжения.

Рис. 23. Разложение аэродинамической силы по осям связанной и скоростной систем координат при Р = О
В дальнейшем мы будем иметь дело в основном с проекциями аэродинамической силы на оси скоростной системы координат. Воспользовавшись формулой (32), запишем выражения для этих проекций. При этом в качестве
характерной будем брать характерную площадь того элемента, который играет основную роль в создании данной силы.
Так, сила лобового сопротивления самолета складывается из сил лобового сопротивления фюзеляжа, крыла, оперения и других частей самолета. За характерную площадь можно принять площадь миделевого сечения фюзеля- жа ^м.ф-

(34)
pV2
у —Г нq
а ^ха °м.ф ->
где Сха - коэффициент лобового сопротивления.
В создании подъемной силы самолета основную роль играет крыло, поэтому в качестве характерной берется площадь крыла S^:

(35)
pV2
у — С нQ
1 а уа °кр 5
где Суа - коэффициент подъемной силы.
Аэродинамическая боковая сила в основном определяется вертикальным оперением и фюзеляжем, значительно меньший вклад в создание этой силы вносят крыло, горизонтальное оперение и другие части самолета. Поскольку вертикальное оперение является основным элементом при создании боковой силы (оно для этого предназначено), то его площадь SB 0 и принимают за характерную:

(36)
, рУ2 <,
za ^в.о?
где Cza - коэффициент боковой силы.
Так как аэродинамические моменты, действующие на самолет, рассчитываются в основном относительно связанных осей координат, найдем проекции момента М на оси связанной системы координат (см. рис. 24).

Аэродинамический момент относительно оси ОХ называется моментом крена. Он определяется в основном силами, действующими на крыло самолета и в меньшей степени - на вертикальное и горизонтальное оперения:
рИ2
(37) где тх - коэффициент момента крена.
Аэродинамический момент относительно оси ОУ называется моментом рыскания. Он создается силами, действующими в основном на вертикальное оперение и фюзеляж. Этот момент вычисляется по следующей формуле:
рИ2
M* = myX^-S в.о£в.о, (38)
где mv - коэффициент момента рыскания;
£в.о - плечо вертикального оперения (расстояние от точки приложения аэродинамической силы, возникающей на вертикальном оперении, до центра масс самолета).
Аэродинамический момент относительно оси 0 Z называется моментом тангажа. Он создается силами, действующими на крыло, горизонтальное оперение и фюзеляж. Вертикальное оперение практически не участвует в создании момента тангажа. Момент тангажа вычисляют по формуле:
рИ2
Mz = mz —, (39)
где mz - коэффициент момента тангажа.
-
Подъемная сила
Рассмотрим обтекание двояковыпуклого симметричного профиля идеальным газом (см. рис. 25). Профиль считается симметричным, если он симметричен относительно хорды. Пусть он сначала установлен под углом атаки ос = 0. В данном случае угол атаки равен углу между вектором скорости набегающего потока V и хордой профиля.

Рис. 25. Обтекание симметричного профиля при ос = О (без образования подъемной силы)
У носка профиля в передней критической точке А происходит полное торможение потока, статическое давление в этой точке максимально и равно полному давлению. Далее поток разделяется на два: один обтекает верхнюю поверхность профиля, другой - нижнюю. У задней кромки профиля потоки опять сливаются в задней критической точке В. В точке В также как и в точке А скорость потока равна 0, потому что здесь сходятся линии тока, идущие по верхней и нижней поверхностям профиля, а частица газа не может одновременно двигаться по двум направлениям. Следовательно, в точке В статическое давление также как и в точке А максимально и равно полному давлению. Но между точками А и В статическое давление отличается от полного давления. Это является следствием того, что в процессе движения от точки А к точке В площади поперечных сечений струек сначала уменьшаются, а потом растут. При этом в соответствии с уравнением неразрывности (10) скорость в струйках будет соответственно сначала расти, а затем падать. Из закона сохранения энергии в аэродинамике (см. уравнение Бернулли (16)) следует, что при увеличении скорости статическое давление уменьшается. Значит, от точки А до точки В на верхней и нижней поверхностях профиля будут располагаться зоны относительного разрежения. Поскольку мы рассматриваем симметричный профиль, то величины падения статического давления в этих зонах будут одинаковыми. Это значит, что в направлении, перпендикулярном вектору скорости набегающего потока, на профиль не будет воздействовать составляющая аэродинамической силы, названная выше подъемной.
Очевидно, что для того, чтобы получить подъемную силу нужно сделать профиль несимметричным или установить симметричный профиль под некоторым углом атаки ос ф 0 (см. рис. 26).
Рассмотрим обтекание профиля потоком под углом атаки ос > 0. В этом случае струйка, обтекающая профиль сверху будет иметь большее сужение,
чем струйка, обтекающая профиль снизу, а значит скорость в верхней струйке будет больше, чем в нижней (VB > VH). Это приведет к тому, что на верхней поверхности профиля статическое давление будет меньше, чем на нижней (ръ < /?„). Из-за этой разности образуется аэродинамическая подъемная сила, направленная вверх.

а) обтекание несимметричного профиля при ос = О

б) обтекание симметричного профиля при ос > О
Рис. 26. Обтекание профилей с образованием подъемной силы
Естественно предположить, что чем больше угол атаки или вогнутость профиля, тем больше будет и подъемная сила. Рассмотрим вначале влияние угла атаки на подъемную силу симметричного профиля. В формуле подъемной силы (35) имеется коэффициент, который зависит от угла атаки - это коэффициент подъемной силы Cva. График зависимости Cva от ос для симметричного и несимметричного профилей представлен на рис. 27, из которого видно, что при малых углах атаки коэффициент подъемной силы зависит от ос линейно.

Рис. 27. Зависимость коэффициента подъемной силы от угла атаки
Если профиль имеет положительную относительную вогнутость, то кривая Cva = /(ос) смещается плоскопараллельно вверх. Угол атаки, при котором Суа = О обозначается ОСО, в данном случае осо< 0. Легко видеть, что при одном и том же угле атаки профиль, имеющий большую относительную вогнутость, будет иметь больший коэффициент подъемной силы.
На больших углах атаки нарушается плавное обтекание профиля. Это происходит из-за влияния вязкости на движение частиц в пограничном слое. В процессе движения вдоль верхней поверхности профиля частицы воздуха будут терять скорость. На каком-то этапе им не хватит кинетической энергии, чтобы двигаться дальше вдоль поверхности. В итоге на некотором участке верхней поверхности профиля произойдет отрыв пограничного слоя. Это явление приводит к нарушению линейности зависимости Cva = /(ос). При увеличении угла атаки зона отрыва также будет увеличиваться, но коэффициент подъемной силы Суа при этом продолжает расти и достигает своего максимального значения С/тах. Угол атаки, который соответствует Суатах, называется критическим углом атаки оскр (см. рис. 28). Величина критического угла атаки, как правило, не превышает 20°. При дальнейшем увеличении угла атаки отрыв потока достигнет интенсивности, при которой коэффициент подъемной силы будет резко падать.

Рис. 28. Соответствие максимального значения коэффициента подъемной силы критическому углу атаки
-
Сила лобового сопротивления
Выше мы отметили, что сила лобового сопротивления складывается из сил, действующих на все части самолета, обтекаемые потоком. Но для упрощения и сокращения объема излагаемого материала рассмотрим только силу лобового сопротивления, возникающую на крыле самолета. Соответственно в качестве характерной площади будем использовать площадь крыла.
Сила лобового сопротивления крыла складывается из сил различной природы. В общем случае силу лобового сопротивления можно представить в виде следующей суммы:
Ха= X а тр + X а д + X а j + X а вл (40)
где Хатр - сила сопротивления трения;
Хал - сила сопротивления давления;
Xai - сила индуктивного сопротивления;
1 2 3 4 5 6