Файл: Audio and Radio Engineering.pdf

6-36 Digital Coding of Audio Signals

The inverse Laplace transform performs the reverse mapping. Laplace transforms are useful for
analog design.

The Fourier transform is a special kind of Laplace transform; it maps a time domain function

x(t) into a frequency domain function X(jw), where X(jw) describes the spectrum (frequency
response) of the signal x(t). The Fourier transform takes the form

(6.4.8)

This equation (and the inverse Fourier transform), are identical to the Laplace transforms

when 

S

= jw; the Laplace transform equals the Fourier transform when the real part of s is zero.

The Fourier series is a special case of the Fourier transform and results when a signal contains
only discrete frequencies, and the signal is periodic in the time domain.

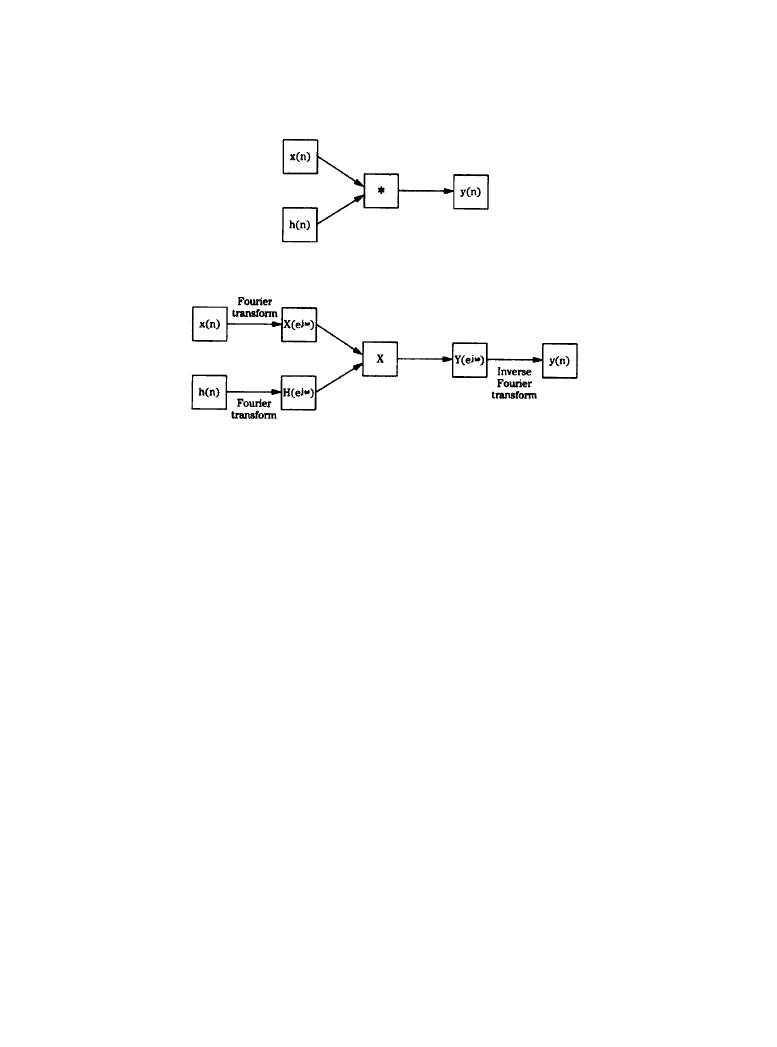
Figure 6.4.4 shows how transforms are used. Specifically, two methods can be used to com-

pute an output signal: convolution in the time domain, and multiplication in the frequency
domain. Although convolution is conceptually concise, in practice, the second method using
transforms and multiplication in the frequency domain is usually preferable. Transforms also are
invaluable in analyzing a signal, to determine its spectral characteristics. In either case, the effect
of filtering a discrete signal can be predictably known.

The Fourier transform for discrete signals generates a continuous spectrum but is difficult to

compute. Thus, a sampled spectrum for discrete time signals of finite duration is implemented as

X j

ω

( )

x t

( )e

j

ωt

–

t

d

x

–

x

∫

=

(

a)

(

b)

Figure 6.4.4

 Given an input signal 

x(n) and impulse response h(n) the output signal y(n) can be

calculated through: (

a) direct convolution, or (b) Fourier transformation, multiplication, and inverse

Fourier transformation. In practice, the latter method is often an easier calculation. (

From [1]. Used

with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

DSP Devices and Systems

DSP Devices and Systems 6-37

the discrete Fourier transform (DFT). Just as the Fourier transform generates the spectrum of a
continuous signal, the DFT generates the spectrum of a discrete signal, expressed as a set of har-
monically related sinusoids with unique amplitude and phase. The DFT takes samples of a wave-
form and operates on them as if they were an infinitely long waveform comprised of sinusoids,
harmonically related to a fundamental frequency corresponding to the original sample period.
An inverse DFT can recover the original sampled signal.

The DFT is the Fourier transform of a sampled signal. When a finite number of samples (N)

are considered, the N-point DFT transform is expressed as

(6.4.9)

The X(m) term is often called bin m and describes the amplitude of the frequencies in signal

x(n), computed at N equally spaced frequencies. The m = 0, or bin 0 term describes the dc con-
tent of the signal, and all other frequencies are all harmonically related to the fundamental fre-
quency corresponding to m = 1, or bin 1. Bin numbers thus specify the harmonics that comprise
the signal, and the amplitude in each bin describes the power spectrum (square of the amplitude).
The DFT thus describes all the frequencies contained in signal x(n). There are identical positive
and negative frequencies; usually only the positive half is shown, and multiplied by 2 to obtain
the actual amplitudes.

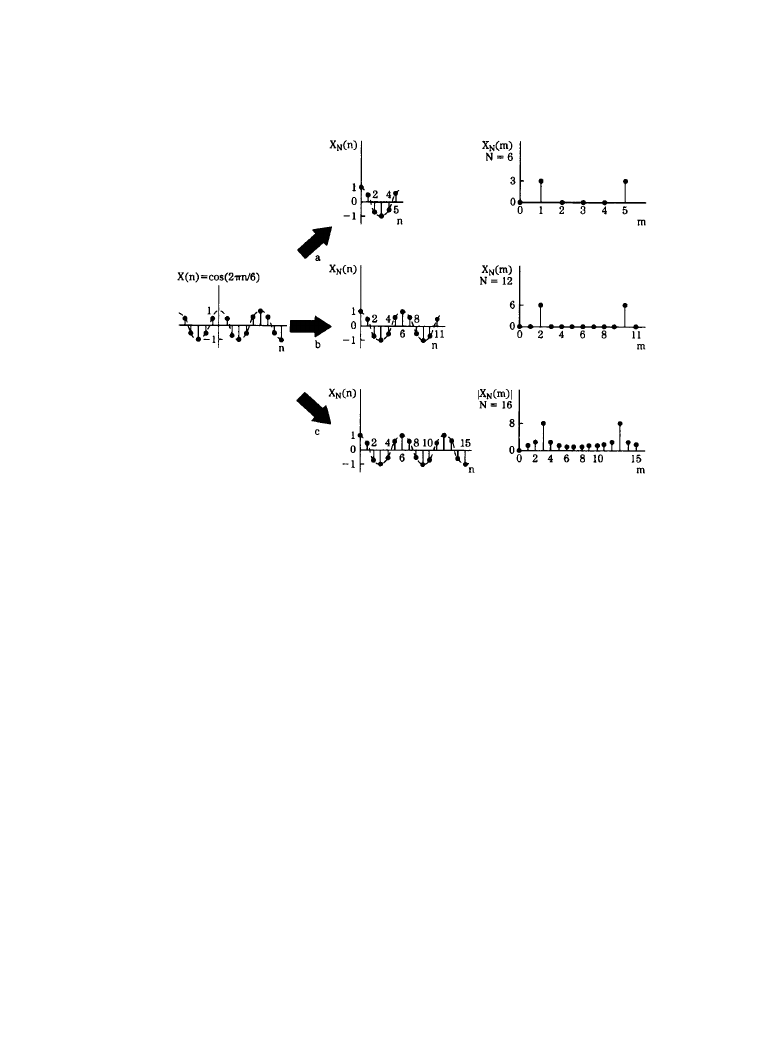
An example of DFT operations is shown in Figure 6.4.5. The input signal to be analyzed is a

simple periodic function x(n) = cos(2

πn/6). The function is periodic over six samples because

x(n) = x(n + 6). Three N-point DFTs are used, with N = 6, 12, and 16. In the first two cases, N is
equal to 6 or is an integer multiple of 6; a larger N yields greater spectral resolution. In the third
case, N = 16, the discrete spectrum positions cannot exactly represent the input signal; spectral
leakage occurs in all bins. In all cases, the spectrum is symmetrical.

The DFT is computation-intensive, requiring N

2

 complex multiplications and N(N – 1) com-

plex additions. The DFT is often generated with the fast Fourier transform (FFT), a collection of
fast and efficient algorithms for spectral computation that takes advantage of computational
symmetries and redundancies in the DFT; it requires Nlog

2

N computations, 100 times fewer than

DFT. The FFT can only be used when N is an integral power of 2; zero samples can be padded to
satisfy this requirement. The FFT is not another type of transformation, but rather an efficient
method of calculating the DFT. In general, a number of short length DFTs are calculated, then
the results are combined. The FFT can be applied to various calculation methods and strategies,
including analysis of signals and filter design.

The FFT will transform a time series, such as the impulse response of a network, into the real

and imaginary parts of the impulse response in the frequency domain. In this way, the magnitude
and phase of the network's transfer function can be obtained. An inverse FFT can produce a time
domain signal. FFT filtering is accomplished through multiplication of spectra. The impulse
response of the filter is transformed to the frequency domain. Real and imaginary arrays,
obtained by FFT transformation of overlapping segments of the signal, are multiplied by filter
arrays, and an inverse FFT produces a filtered signal. Because the FFT can be efficiently com-
puted, it can be used as an alternative to time domain convolution if the overall number of multi-
plications is fewer.

X m

( )

x n

( )e

j 2

π/N

(

)

–

(

)mn

n

0

=

N

1

–

∑

=

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

DSP Devices and Systems

6-38 Digital Coding of Audio Signals

The z-transform operates on discrete signals in the same way that the Laplace transform oper-

ates on continuous signals. In the same way that the Laplace transform is a generalization of the
Fourier transform, the z-transform is a generalization of the DFT. Whereas the Fourier transform
operates on a particular complex value e

–jw

the  z-transform operates with any complex value.

When z = e

jw

, the z-transform is identical to the Fourier transform. The DFT is thus a special case

of the z-transform. The z-transform of a sequence x(n) is defined as

(6.4.10)

where  z is a complex variable and z

–1

represents a unit delay element. The z-transform has an

inverse transform, often obtained through partial fraction expansion.

Whereas the DFT is used for literal operations, the z-transform is a mathematical tool used in

digital signal processing theory. Convolution in the time domain is equivalent to multiplication in
the z-domain. For example, we could take the z-transform of the convolution equation, such that
the z-transform of an input multiplied by the z-transform of a filter’s impulse response is equal to
the z-transform of the filter output. In other words, the ratio of the filter output transform to the
filter input transform—that is, the transfer function H(z)—is the z-transform of the impulse

X z

( )

x n

( )z

n

–

n

x

–

=

x

∑

=

Figure 6.4.5

 Examples of a periodic signal applied to an 

N-point DFT for three different values of

N. Greater resolution is obtained as N is increased. When N is not equal to an integral number of
waveform periods, spectral leakage occurs. (

van den Enden and Verhoeckx. From [1]. Used with

permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

DSP Devices and Systems

DSP Devices and Systems 6-39

response. Furthermore, this ratio, the transfer function H(z), is a fixed function determined by
the filter. In the z-domain, given an impulse input, the transfer function equals the output.

6.4.2e

Unit Circle and Region of Convergence

The Fourier transform of a discrete signal corresponds to the z-transform on the unit circle in the
z-plane. The equation z = e

jw

defines the unit circle in the complex plane. The evaluation of the

z-transform along the unit circle yields the frequency response of the function.

The variable z is complex, and X(z) is the function of the complex variable. The set of z in the

complex plane for which the magnitude of X(z) is finite is said to be in the region of conver-
gence. The set of z in the complex plane for which the magnitude of X(z) is infinite is said to
diverge, and is outside the region of convergence. The function X(z) is defined over the entire z-
plane but is only valid in the region of convergence. The complex variable s is used to describe
complex frequency; this is a function of the Laplace transform. The s variable lies on the com-
plex s-plane. The s-plane can be mapped to the z-plane; vertical lines on the s-plane map as cir-
cles in the z-plane.

Because there is a finite number of samples, practical systems must be designed within the

region of convergence. The unit circle is the smallest region in the z-plane that falls within the
region of convergence for all finite stable sequences. Poles must be placed inside the unit circle
on the z-plane for proper stability. Improper placement of the poles constitutes an instability.

Mapping from the s-plane to the z-plane is an important process. Theoretically, this function

allows the designer to choose an analog transfer function and find the z-transform of that func-
tion. Unfortunately, the s-plane generally does not map into the unit circle of the z-plane. Stable
analog filters, for example, do not always map into stable digital filters. This is avoided by multi-
plying by a transform constant, used to match analog and digital frequency response. There also
is a nonlinear relationship between analog and digital break frequencies that must be accounted
for. The nonlinearities are known as warping effects and the use of the constant is known as pre-
warping the transfer function.

Often, a digital implementation can be derived from an existing analog representation. For

example, a stable analog filter can be described by the system function H(s). Its frequency
response is found by evaluating H(s) at points on the imaginary axis of the s-plane. In the func-
tion H(s), s can be replaced by a rational function of z, which will map the imaginary axis of the
s-plane onto the unit circle of the z-plane. The resulting system function H(z) is evaluated along
the unit circle and will take on the same values of H(s) evaluated along its imaginary axis.

6.4.2f

Poles and Zeros

Summarizing, the transfer function H(z) of a linear, time-invariant discrete-time filter is defined
to be the z-transform of the impulse response h(n). The spectrum of a function is equal to the z-
transform evaluated on the unit circle. The transfer function of a digital filter can be written in
terms of its z transform; this permits analysis in terms of the filter’s poles and zeros. The zeros
are the roots of the numerator’s polynomial of the transfer function of the filter, and the poles are
the denominator’s roots. Mathematically, zeros make H(z) = 0, and poles make H(z) nonanalytic.
When the magnitude of H(z) is plotted as a function of z, poles appear at a distance above the z-
plane and zeros touch the z-plane. One might imagine the flat z-plane and above it a flexible con-
tour—the magnitude transfer function—passing through the poles and zeros, with peaks on top

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

DSP Devices and Systems

6-40 Digital Coding of Audio Signals

of poles, and valleys centered on zeros. Tracing the rising and falling of the contour around the
unit circle yields the frequency response. For example, the gain of a filter at any frequency can
be measured by the magnitude of the contour. The phase shift at any frequency is the angle of the
complex number that represents the system response at that frequency.

If we plot 

 on the complex plane, we get the unit circle; 

 specifies all points on

the complex plane that lie outside the unit circle; and 

 specifies all points inside it. The z-

transform of a sequence can be represented by plotting the locations of the poles and zeros on the
complex plane.

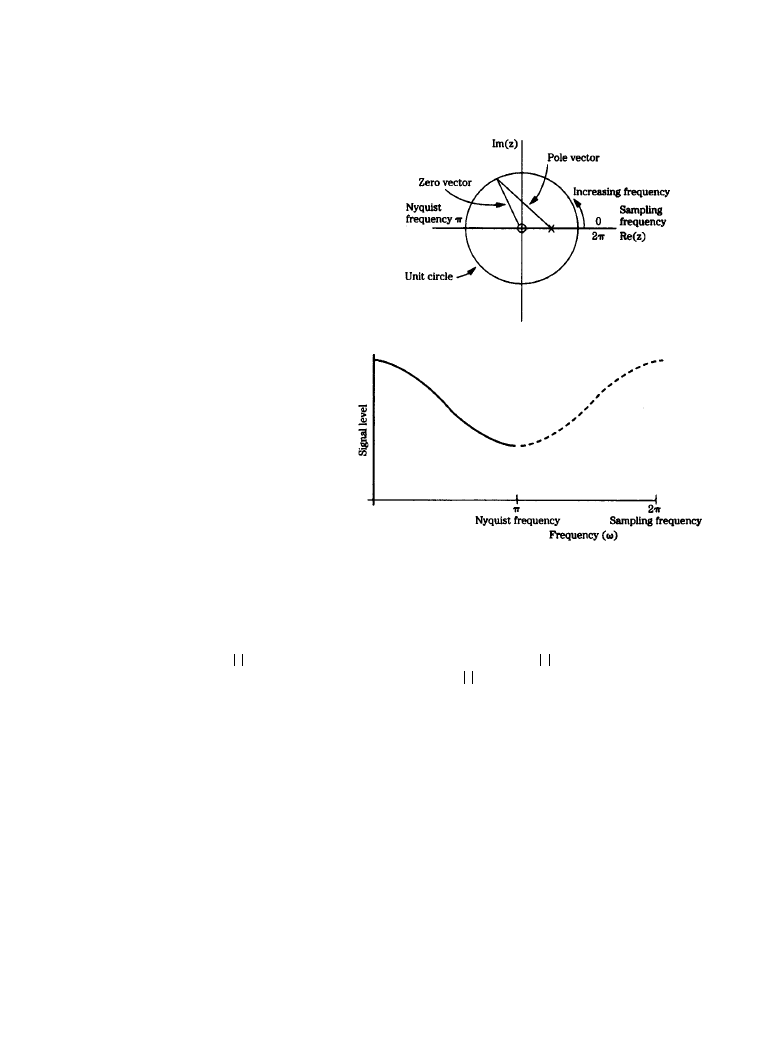
Figure 6.4.6a shows an example of a z-plane plot. Among other approaches, the response can

be analyzed by examining the relationships between the pole and zero vectors. In the z-plane,
angular frequency is represented as an angle, with a rotation of 360° corresponding to the sam-
pling frequency. The Nyquist frequency is thus located at 

π in the figure. The example shows a

single pole (X) and zero (0). The amplitude of the frequency response can be determined by
dividing the magnitude of the zero vector by that of the pole vector. The frequency response from
0 to the Nyquist frequency is seen to be that of a lowpass filter, as shown in Figure 6.4.6b. Simi-
larly, the phase response can be determined by subtracting the argument of the pole vector from
that of the zero vector. As the positions of the pole and zero are varied, the response of the filter
changes. For example, if the pole is moved along the negative real axis, the filter's response
changes to that of a highpass filter.

Zeros are created by summing input samples, and poles are created by feedback. The order of

a filter is equal to the number of poles or zeros it exhibits, whichever is greater. A filter is stable

z

1

=

z

1

>

z

1

<

Figure 6.4.6

 The frequency

response of a filter can be
obtained by dividing the magni-
tude of the zero vector by that of
the pole vector: (

a) an example

of a 

z-plane plot of a lowpass fil-

ter showing the pole and zero
locations, (

b) examination of the

plot reveals the filter frequency
response. (

From [1]. Used with

permission.)

(

a)

(

b)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

DSP Devices and Systems