Файл: Audio Power Amp Design Handbook.pdf

Audio Power Amplifier Design Handbook

increasing from 0.10% to 0.16%; for 10% imbalance this deteriorates badly
to 0.55%. Unsurprisingly, imbalance in the other direction (Ic1>Ic2) gives
similar results.

Imbalance  defined  as  deviation  of  Ic  (per  device)  from  that  value  which
gives equal currents in the pair.

This  explains  the  complex  distortion  changes  that  accompany  the
apparently  simple  experiment  of  altering  the  value  of  R2

[3]

.  We  might

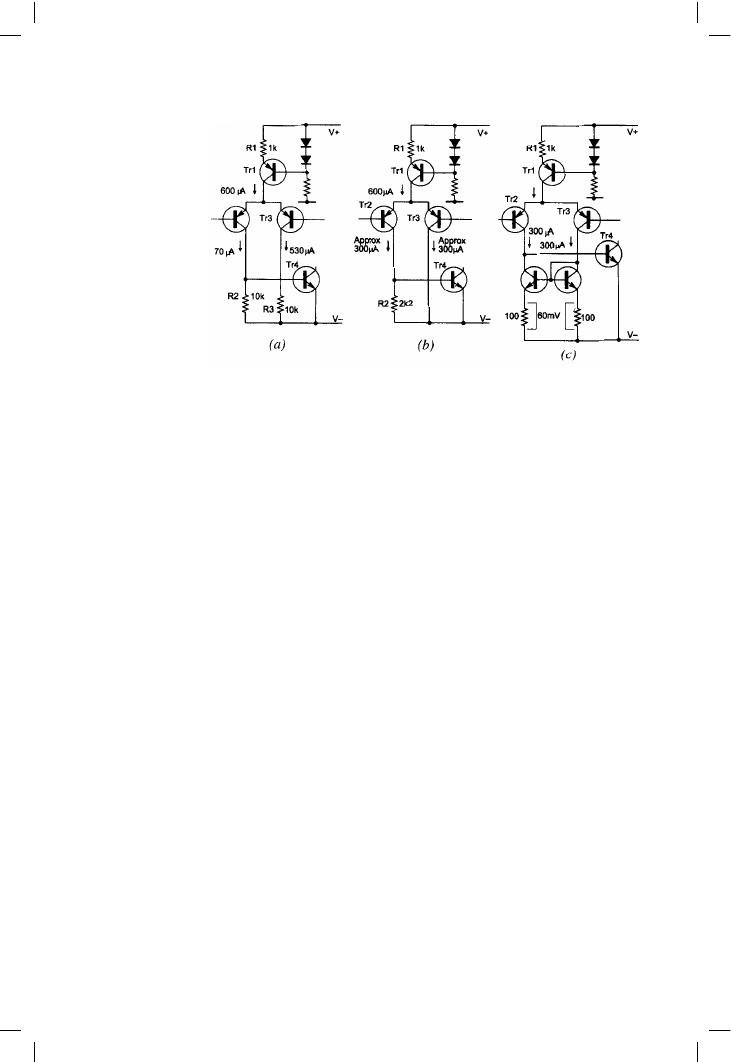
design an input stage like Figure 4.7a, where R1 has been selected as 1k
by uninspired guesswork and R2 made highish at 10k in a plausible but
misguided  attempt  to  maximise  o/l  gain  by  minimising  loading  on  Q1
collector.  R3  is  also  10k  to  give  the  stage  a  notional  balance,  though
unhappily this is a visual rather than electrical balance. The asymmetry is
shown  in  the  resulting  collector  currents;  the  design  generates  a  lot  of
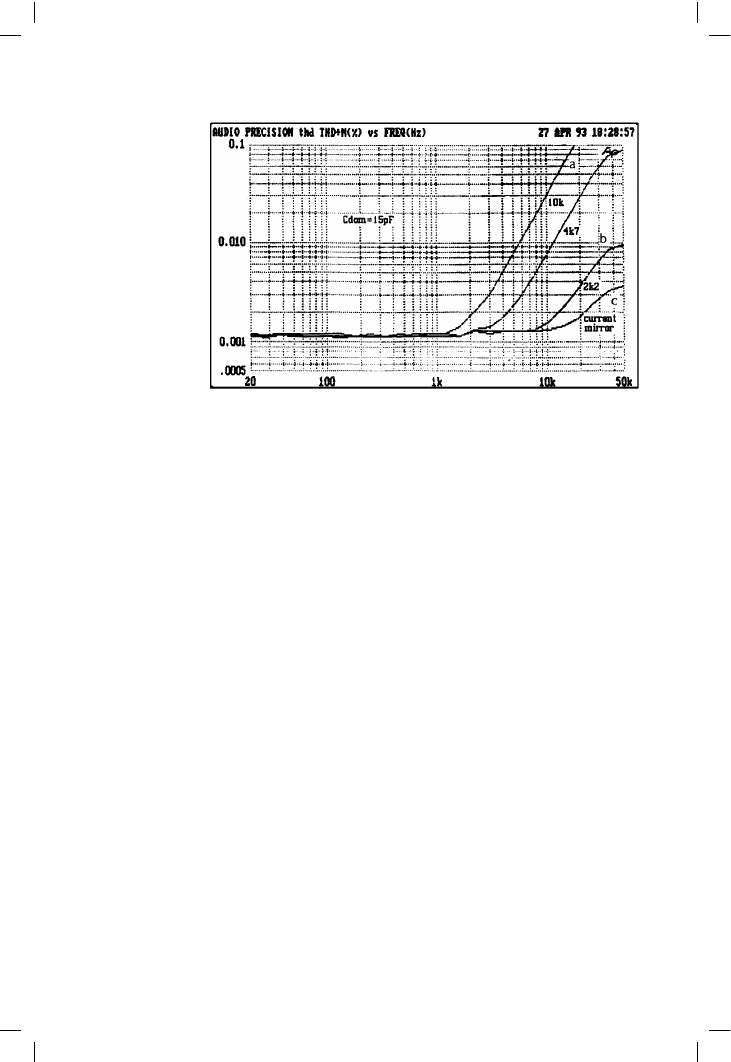
avoidable  second  harmonic  distortion,  displayed  in  the  10k  curve  of
Figure  4.8.

Recognising  the  crucial  importance  of  DC  balance,  the  circuit  can  be
rethought as Figure 4.7b. If the collector currents are to be roughly equal,
then R2 must be about 2 

× R1, as both have about 0.6 V across them. The

dramatic effect of this simple change is shown in the 2k2 curve of Figure
4.8; the improvement is accentuated as the o/l gain has also increased by
some 7 dB, though this has only a minor effect on the closed-loop linearity
compared with the improved balance of the input pair. R3 has been excised
as it contributes very little to input stage balance.

The joy of current-mirrors

Although  the  input  pair  can  be  approximately  balanced  by  the  correct
values for R1 and R2, we remain at the mercy of several circuit tolerances.
Figure  4.6  shows  that  balance  is  critical,  needing  an  accuracy  of  1%  or

80

Figure 4.7

Improvements to the
input pair. a Poorly
designed version.
b Better; partial
balance by correct
choice of R2. c Best;
near-perfect Ic
balance enforced by
mirror

The small signal stages

better for optimal linearity and hence low distortion at HF, where the input
pair  works  hardest.  The  standard  current-mirror  configuration  in  Figure
4.7c forces the two collector currents very close to equality, giving correct
cancellation of the second harmonic; the great improvement that results is
seen in the current-mirror curve of Figure 4.8. There is also less DC offset
due  to  unequal  base-currents  flowing  through  input  and  feedback
resistances;  I  often  find  that  a  power-amplifier  improvement  gives  at
least  two  separate  benefits.  This  simple  mirror  has  well-known  residual
base-current  errors  but  they  are  not  large  enough  to  affect  the  distortion
performance.

The hyperbolic-tangent law also holds for the mirrored pair

[4]

, though the

output  current  swing  is  twice  as  great  for  the  same  input  voltage  as  the
resistor-loaded version. This doubled output is given at the same distortion
as for the unmirrored version, as linearity depends on the input voltage,
which has not changed. Alternatively, we can halve the input and get the
same  output,  which  with  a  properly  balanced  pair  generating  third
harmonic only will give one-quarter the distortion. A pleasing result.

The input mirror is made from discrete transistors, regretfully foregoing the
Vbe-matching  available  to  IC  designers,  and  it  needs  its  own  emitter-
degeneration for good current-matching. A voltage-drop across the current-
mirror emitter-resistors in the range 30–60 mV will be enough to make the
effect of Vbe tolerances on distortion negligible; if degeneration is omitted
then  there  is  significant  variation  in  HF  distortion  performance  with
different specimens of the same transistor type.

Putting a current-mirror in a well-balanced input stage increases the total
o/l gain by at least 6 dB, and by up to 15 dB if the stage was previously
poorly  balanced;  this  needs  to  be  taken  into  account  in  setting  the

81

Figure 4.8

Distortion of model
amplifier:
a Unbalanced with
R2 = 10k. b Partially
balanced with R =
2k2. c Accurately
balanced by current-
mirror

Audio Power Amplifier Design Handbook

compensation. Another happy consequence is that the slew-rate is roughly
doubled, as the input stage can now source and sink current into Cdom
without wasting it in a collector load. If Cdom is 100 pF, the slew-rate of
Figure 4.7b is about 2.8 V/µsec up and down, while 4.7c gives 5.6 V/µsec.
The  unbalanced  pair  at  4.7a  displays  further  vices  by  giving  0.7 V/µsec
positive-going and 5 V/µsec negative-going.

Improving input-stage linearity

Even  if  the  input  pair  has  a  current-mirror,  we  may  still  feel  that  the  HF
distortion needs further reduction; after all, once it emerges from the noise
floor it octuples with each doubling of frequency, and so it is well worth
postponing the evil day until as far as possible up the frequency range. The
input pair shown has a conventional value of tail-current. We have seen
that the stage transconductance increases with Ic, and so it is possible to
increase  the  gm  by  increasing  the  tail-current,  and  then  return  it  to  its
previous value (otherwise Cdom would have to be increased proportion-
ately to maintain stability margins) by applying local NFB in the form of
emitter-degeneration resistors. This ruse powerfully improves input linear-
ity,  despite  its  rather  unsettling  flavour  of  something-for-nothing.  The
transistor  non-linearity  can  here  be  regarded  as  an  internal  non-linear
emitter resistance re, and what we have done is to reduce the value of this
(by increasing Ic) and replaced the missing part of it with a linear external
resistor Re.

For a single device, the value of re can be approximated by:

re = 25/Ic ohms (for Ic in mA)

Equation 4.3

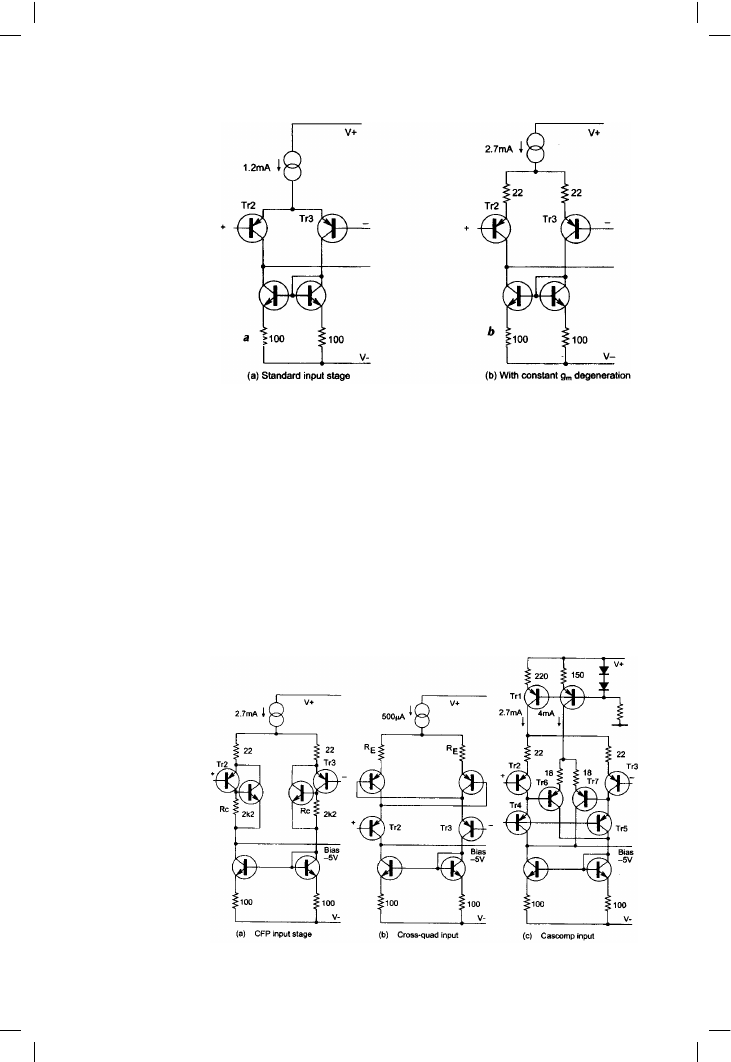
Our original stage at Figure 4.9a has a per-device Ic of 600 µA, giving a
differential (i.e. mirrored) gm of 23 mA/V and re = 41.6 !. The improved
version  at  Figure  4.9b  has  Ic  =  1.35 mA  and  so  re  =  18.6 !;  therefore
emitter degeneration resistors of 22 ! are required to reduce the gm back
to its original value, as 18.6 + 22 = 41.6 !. The distortion measured by the
circuit of Figure 4.4 for a –40 dBu input voltage is reduced from 0.32% to
0.032%,  which  is  an  extremely  valuable  linearisation,  and  will  translate
into a distortion reduction at HF of about 5 times for a complete amplifier;
for reasons that will emerge later the full advantage is rarely gained. The
distortion remains a visually pure third-harmonic, so long as the input pair
remains balanced. Clearly this sort of thing can only be pushed so far, as the
reciprocal-law reduction of re is limited by practical values of tail current.
A name for this technique seems to be lacking; constant-gm degeneration
is descriptive but rather a mouthful.

The standing current is roughly doubled so we have also gained a higher
slew-rate; it has theoretically increased from 10 V/µsec to 20 V/µsec, and
once  again  we  get  two  benefits  for  the  price  of  one  inexpensive
modification.

82

The small signal stages

Radical methods of improving input linearity

If we are seeking still better linearity, various techniques exist. Whenever it
is needful to increase the linearity of a circuit, it is often a good approach
to increase the local feedback factor, because if this operates in a tight local
NFB loop there is often little effect on the overall global-loop stability. A
reliable  method  is  to  replace  the  input  transistors  with  complementary-
feedback (CFP or Sziklai) pairs, as shown in the stage of Figure 4.10a. If an
isolated  input  stage  is  measured  using  the  test  circuit  of  Figure  4.4,  the
constant-gm degenerated version shown in Figure 4.9b yields 0.35% third-
harmonic  distortion  for  a  –30 dBu  input  voltage,  while  the  CFP  version

83

Figure 4.9

Input pairs before and
after constant-gm
degeneration, showing
how to double stage
current while keeping
transconductance
constant; distortion is
reduced by about ten
times

Figure 4.10

Some enhanced
differential pairs: a The
Complementary
Feedback Pair. b The
Cross-quad. c The
Cascomp

Audio Power Amplifier Design Handbook

gives 0.045%. (Note that the input level here is 10 dB up on the previous
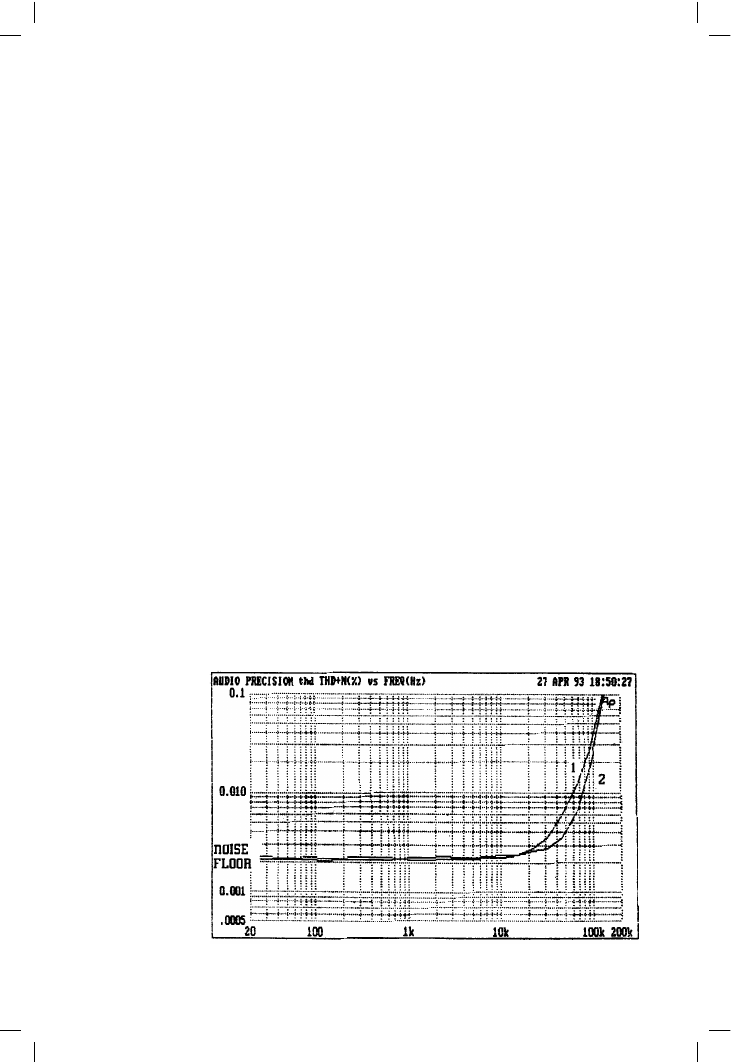
example, to get well clear of the noise floor.) When this stage is put to work
in a model amplifier, the third-harmonic distortion at a given frequency is
roughly  halved,  assuming  all  other  distortion  sources  have  been  appro-
priately minimised. However, given the high-slope of input-stage distortion,
this only extends the low-distortion regime up in frequency by less than an
octave. See Figure 4.11.

A compromise is required in the CFP circuit on the value of Rc, which sets
the proportion of the standing current that goes through the NPN and PNP
devices on each side of the stage. A higher value of Rc gives better linearity,
but more noise, due to the lower Ic in the NPN devices that are the inputs
of the input stage, as it were, causing them to match less well the relatively
low source resistances. 2k2 is a good compromise.

Several  other  elaborations  of  the  basic  input  pair  are  possible,  although
almost  unknown  in  the  audio  community.  We  are  lucky  in  power-amp
design  as  we  can  tolerate  a  restricted  input  common-mode  range  that
would  be  unusable  in  an  op-amp,  giving  the  designer  great  scope.
Complexity in itself is not a serious disadvantage as the small-signal stages
of the typical amplifier are of almost negligible cost compared with mains
transformers, heatsinks, etc.

Two established methods to produce a linear input transconductance stage
(referred to in op-amp literature simply as a transconductor) are the cross-
quad

[5]

and the cascomp

[6]

configurations. The cross-quad (Figure 4.10b)

gives a useful reduction in input distortion when operated in isolation but
is hard to incorporate in a practical amplifier because it relies on very low
source-resistances  to  tame  the  negative  conductances  inherent  in  its
operation. The cross-quad works by imposing the input voltage to each half

84

Figure 4.11

Whole-amplifier THD
with normal and CFP
input stages; input
stage distortion only
shows above noise
floor at 20 kHz, so
improvement occurs
above this frequency.
The noise floor
appears high as the
measurement
bandwidth is 500 kHz