Сабақ №9		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқан оқушы саны:	Қатыспаған оқушы саны:
Сабақтың тақырыбы		Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Оқу бағдарламасына сәйкес оқыту мақсаттары		11.3.1.2 - анықталмаған интеграл қасиеттерін білу және қолдану;
Сабақтың мақсаты:		Интегралдау әдістерін білу және есеп шығаруда қолдану.
Сабақтың кезеңі	Педагогтің әрекеті			Оқушының әрекеті	Бағалау	Ресурстар
Басы 5 минут	Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. .			Психологиялық ахуалға берілген тапсырманы орындайды.		Психологиялық ахуал.
Негізгі бөлім Тақырыпты ашу 10 минут	Алғашқы функция ұғымы. Ғылым мен техниканың түрлі-түрлі салаларындағы көптеген мәселелерді шешу туындысы берілген функцияны табуға әкеліп соқтырады. Сондықтан математикада жаңа бір операция, интегралдау операциясы қарастырылады. Ізделіп отырған F(x) функциясының берілген туындысы f(x) бойынша сол F(x) функциясын табу мәселесі тек интегралдау операциясының  жәрдемімен шешіледі. Міне осы  F(x)-ті берілген функция f(x)-тің алғашқы функциясы деп атайды. Анықтама. Егер бір аралықтың әрбір нүктесінде функция F(x) үшін dF(x)=f(x)dx теңдігі орындалса, F(x) функциясы f(x)-тің сол аралықтағы алғашқы функциясы деп аталады. Мысалы:  F(x)=x7   бүкіл сандар осі бойында  f(x)=7x6  функциясының алғашқы функциясы болады, өйткені х-тің кез келген мәнінде   (x7)’=7x6. Ал функция   F(x)=lnx  функция    f(x)=1/x  үшін алғашқы функция болады өйткені (lnx)’=1/x			Ішкі және сыртқы шеңбердегі оқушылардың берілген сұрақтарға жауабын саралау. Сыртқы шеңбердегі оқушыларды 1- топқа, ішкі шеңбердегі оқушыларды 2-топқа отырғызамын	Мұғалім ОМ анықтайды	Үлестірмелі қағаздар
Оқулықпен жұмыс 25 минут	Осы көрсетілген форуларды пайдаланып функцияның анықталмаған интегралын табуға мысалдар қарастырайық:  1.  интегралын есептеу керек. Шешуі. (3) формула бойынша 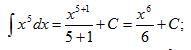 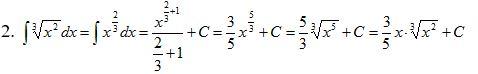интегралын табу керек. Шешуі: Интеграл астындағы өрнекті жақшаны ашып мына түрге келтіреміз: Қосындының интегралын интегралдардың қосындысымен ауыстырсақ,  болады Үшінші интегралдағы тұрақты көбейткішті интеграл табысының алдына шығарсақ,   түрге  келеді (2) және (3) формулаларды қолдансақ 4. 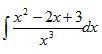       интегралын табу керек Шешуі: Бөлшектің алымын бөліміне мүшелеп бөліп, алдыңғы мысалдағыдай есептейміз 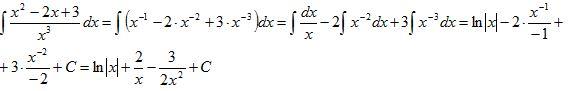Берілген интегралды интенгралдардың қосындысына келтіріп интегралдау қосындысына келтіріп интегралдау әдісін жіктеу әдісі деп атайды. Қарастырылған 3 және 4 мысалдар жіктеу әдісімен шығарылады.			Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді; Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді;	ҚБ «Шаршылар» әдісі әдісі арқылы оқушылар өз-өзін бағалайды	Топтық тапсырмалар.
Соңы 5 минут	Сабақты бекіту Рефлексия Үйге тапсырма:			Сабақты пысықтау тапсырмаларын орындау.
Кері байланыс	Рефлексия (жеке,жұпта,топта, ұжымда)			«Табыс» ағашы. Қызыл алма – сабақ маған түсініксіз. Сары алма – тақырыпты түсіндім, бірақ тез ұмытамын. Жасыл алма – сабақ маған ұнады, тақырыпты меңгердім. (Оқушылар өздері таңдаған алманы алып, ағашқа жапсырады)		Кері байланыс парағы.

---

Сабақ №10		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқан оқушы саны:	Қатыспаған оқушы саны:
Сабақтың тақырыбы		Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Оқу бағдарламасына сәйкес оқыту мақсаттары		11.3.1.3 - негізгі анықталмаған интегралдарды 1. 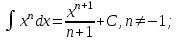2. 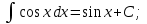3. 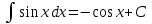; 4. 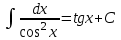; 5. 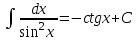білу және оларды есептер шығаруда қолдану;
Сабақтың мақсаты:		Интегралдау әдістерін білу және есеп шығаруда қолдану.
Сабақтың кезеңі	Педагогтің әрекеті			Оқушының әрекеті	Бағалау	Ресурстар
Басы 5 минут	Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. .			Психологиялық ахуалға берілген тапсырманы орындайды.		Психологиялық ахуал.
Негізгі бөлім Тақырыпты ашу 10 минут	Алғашқы функция ұғымы. Ғылым мен техниканың түрлі-түрлі салаларындағы көптеген мәселелерді шешу туындысы берілген функцияны табуға әкеліп соқтырады. Сондықтан математикада жаңа бір операция, интегралдау операциясы қарастырылады. Ізделіп отырған F(x) функциясының берілген туындысы f(x) бойынша сол F(x) функциясын табу мәселесі тек интегралдау операциясының  жәрдемімен шешіледі. Міне осы  F(x)-ті берілген функция f(x)-тің алғашқы функциясы деп атайды. Анықтама. Егер бір аралықтың әрбір нүктесінде функция F(x) үшін dF(x)=f(x)dx теңдігі орындалса, F(x) функциясы f(x)-тің сол аралықтағы алғашқы функциясы деп аталады. Мысалы:  F(x)=x7   бүкіл сандар осі бойында  f(x)=7x6  функциясының алғашқы функциясы болады, өйткені х-тің кез келген мәнінде   (x7)’=7x6. Ал функция   F(x)=lnx  функция    f(x)=1/x  үшін алғашқы функция болады өйткені (lnx)’=1/x Анықталмаған интегралдың негізгі таблицасы Егер u аргумент  х-тің белгілі бір аралықтағы дифференциалданатын функциясы болса, берілген дифференциалдық есептеудің формулаларын пайдаланып, анықталмаған интегралдың ішіндегі негізгілерінің таблицасын жасауға болады. Бұл таблицаға енетін әрбір формуланың дұрыстығын дифференциалдау арқылы дәлелдеп көрсетуге болады.			Ішкі және сыртқы шеңбердегі оқушылардың берілген сұрақтарға жауабын саралау. Сыртқы шеңбердегі оқушыларды 1- топқа, ішкі шеңбердегі оқушыларды 2-топқа отырғызамын	Мұғалім ОМ анықтайды	Үлестірмелі қағаздар
Оқулықпен жұмыс 25 минут				Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді; Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді;	ҚБ «Шаршылар» әдісі әдісі арқылы оқушылар өз-өзін бағалайды	Топтық тапсырмалар.
Соңы 5 минут	Сабақты бекіту Рефлексия Үйге тапсырма:			Сабақты пысықтау тапсырмаларын орындау.
Кері байланыс	Рефлексия (жеке,жұпта,топта, ұжымда)			«Табыс» ағашы. Қызыл алма – сабақ маған түсініксіз. Сары алма – тақырыпты түсіндім, бірақ тез ұмытамын. Жасыл алма – сабақ маған ұнады, тақырыпты меңгердім. (Оқушылар өздері таңдаған алманы алып, ағашқа жапсырады)		Кері байланыс парағы.

---

Сабақ №11		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқан оқушы саны:	Қатыспаған оқушы саны:
Сабақтың тақырыбы		Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Оқу бағдарламасына сәйкес оқыту мақсаттары		11.3.1.3 - негізгі анықталмаған интегралдарды 1. 2. 3. ; 4. ; 5. білу және оларды есептер шығаруда қолдану;
Сабақтың мақсаты:		Интегралдау әдістерін білу және есеп шығаруда қолдану.
Сабақтың кезеңі	Педагогтің әрекеті			Оқушының әрекеті	Бағалау	Ресурстар
Басы 5 минут	Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. .			Психологиялық ахуалға берілген тапсырманы орындайды.		Психологиялық ахуал.
Негізгі бөлім Тақырыпты ашу 10 минут	Анықталмаған интеграл ұғымы F(x) функциясы дифференциалдау деп берілген алғашқы F(x) функциясының  F’(x)= f(x) туындысын немесе df(x)=f(x)dx Дифференциалын табу амалын айтамыз. Сол амалға кері амал, яғни F’(x) болып табылатын берілген f(x) үшін алғашқы F(x) функциясын табу амалы f(x)-ті интегралдау деп аталады. f(x)-ті интегралдау амалын көрсету үшін  символы қолданылады да, былай жазылады: Осы  берілген f(x) функциясының барлық алғашқы функцияларының жиынын бейнелейді және f(x)-тен анықталмаған интеграл деп аталады. Демек, анықтамаға сәйкес болады. Бұл формуладағы F(x) функциясы f(x)-тың белгілі бір алғашқы функциясы, С-кез келген тұрақты. Сонымен бірге f(x)- интеграл астындағы функция, ал f(x)dx – интеграл астындағы өрнек деп аталады.  -символы ұзартылып алынған латын алфавитіндегі S- әріпі, ол символды интегралдың белгісі деп атайды.  Функцияны интегралдау және олардың алғашқы функцияларының қаиеттері жайындағы ілім интегралдық есептеу деп аталады. Дифференциалдық есептеу сияқты интегралдық есептеуде математикалық анализдің өте маңызды бөлімдерінің бірі болып табылды. 1-параграфта қарастырылған есептердің шешуін енді интеграл түрінде былай жазуға болады: 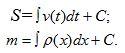4. Анықталмаған интегралдың негізгі қасиеттері F’(x)=f(x) және екенін ескере отырып анықталмаған интегралдың қасиеттерін қарастырамыз. 1.    Дифференциалдың анықталмаған интегралы дифференциалдаған функция мен кез келген тұрақтының қосындысына тең, яғни   2.    Анықталмаған интегралдың дифференциалын интеграл астындағы өрнекке тең, яғни  3.    Тұрақты көбейткішті интегралдық белгінің алдына шығаруға да, интегралдық белгінің астына алып баруға да болады, яғни   4.    Бірнеше функциялардың алгебралық қосындының анықталмаған интегралы қосылғыштардан алынған анықталмаған интегралдардың алгебралық қосындысына тең, яғни			Ішкі және сыртқы шеңбердегі оқушылардың берілген сұрақтарға жауабын саралау. Сыртқы шеңбердегі оқушыларды 1- топқа, ішкі шеңбердегі оқушыларды 2-топқа отырғызамын	Мұғалім ОМ анықтайды	Үлестірмелі қағаздар
Оқулықпен жұмыс 25 минут				Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді; Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді;	ҚБ «Шаршылар» әдісі әдісі арқылы оқушылар өз-өзін бағалайды	Топтық тапсырмалар.
Соңы 5 минут	Сабақты бекіту Рефлексия Үйге тапсырма:			Сабақты пысықтау тапсырмаларын орындау.
Кері байланыс	Рефлексия «СМС» әдісі.			«СМС» Мұғалім сабақты қорытындылау мақсатында оқушылардың сабаққа деген көзқарасын, рефлексиясын тыңдайды.	«СМС»	Кері байланыс

---

Сабақ №12		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқан оқушы саны:	Қатыспаған оқушы саны:
Сабақтың тақырыбы		Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Оқу бағдарламасына сәйкес оқыту мақсаттары		11.3.1.3 - негізгі анықталмаған интегралдарды 1. 2. 3. ; 4. ; 5. білу және оларды есептер шығаруда қолдану;
Сабақтың мақсаты:		Интегралдау әдістерін білу және есеп шығаруда қолдану.
Сабақтың кезеңі	Педагогтің әрекеті			Оқушының әрекеті	Бағалау	Ресурстар
Басы 5 минут	Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. .			Психологиялық ахуалға берілген тапсырманы орындайды.		Психологиялық ахуал.
Негізгі бөлім Тақырыпты ашу 10 минут	Енді анықталмаған интегралды есептеу кезінде жиі қолданылатын әдістердің кейбірін көрсете кетелік. Тура интегралдау. Тура интегралдау деп таблицада келтірілген анықталмаған интегралдар мен анықталмаған интегралдардың қасиеттерін қолданып алғашқы функцияларды табуды айтады. Алмастыру енгізу әдісі. Көп жағдайда жаңа айнымалы енгізгенде (кей алгебралық өрнекті жаңа айнымалы ретінде алғанда) анықталмаған интегралды тура интегралдау әдісімен табуға болады. Бұл әдіс төмендегі теоремаға негізделген. Теорема 1. x=g(t) функциясы бір Т аралығында анықталған және дифференциалданатын функция болсын, ал Х оның мәндерінің жиыны болсын, бұл жиын f(x) функциясының анықталу обылысы болсын. Онда Х аралығында f(x) функциясының алғашқы функциясы бар болса, онда Т жиынында мына формула орындалады: Бұл формула анықталмаған интегралда айнымалыны ауыстыру формуласы деп аталынады. Бөліктеп интегралдау. Бұл әдіс екі функцияның көбейтіндісінің туындысвының формуласының салдары болады. Теорема 2. u(x) және v(x) функциялары бір Х аралығында анықталған дифференциалданатын функциялар болсын, сонымен қатар осы аралықта u’(x)v(x) функциясының алғашқы функциясы бар болсын. Онда Х аралығында u(x)v’(x) функциясының да алғашқы функциясы бар және төмендегі формула орындалады: Бұл формула анықталмаған интегралды бөлектеп есептеу формуласы деп аталынады. Бұл формуланы қолданғанда u(x) функциясы ретінде туынды табуда қарапайым түрге келетін функцияны алады. Көбіне lnx, arctgx, arcsinx функцияларын осы функция ретінде алады. Рационалдық функцияларды (екі көпмүшеліктің қатынасы), иррационалдық функцияларды (радикалдар арқылы өрнектелетін функциялар), трансценденттік функциялары (өрнектерде тригонометриялық, көрсеткіштік функциялар мен олардың әртүрлі комбинациялар бар функциялар) интегралдаған кезде арнайы әдістер қолданылады			Ішкі және сыртқы шеңбердегі оқушылардың берілген сұрақтарға жауабын саралау. Сыртқы шеңбердегі оқушыларды 1- топқа, ішкі шеңбердегі оқушыларды 2-топқа отырғызамын	Мұғалім ОМ анықтайды	Үлестірмелі қағаздар
Оқулықпен жұмыс 25 минут				Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді; Дескриптор: берілген есептің алғашқы функциясын анықтайды; Тригонометриялық өрнектерді шешу барысында заңдылықты ескереді;	ҚБ «Шаршылар» әдісі әдісі арқылы оқушылар өз-өзін бағалайды	Топтық тапсырмалар.
Соңы 5 минут	Сабақты бекіту Рефлексия Үйге тапсырма:			Сабақты пысықтау тапсырмаларын орындау.
Кері байланыс	Рефлексия (жеке,жұпта,топта, ұжымда)			«Табыс» ағашы. Қызыл алма – сабақ маған түсініксіз. Сары алма – тақырыпты түсіндім, бірақ тез ұмытамын. Жасыл алма – сабақ маған ұнады, тақырыпты меңгердім. (Оқушылар өздері таңдаған алманы алып, ағашқа жапсырады)		Кері байланыс парағы.

---

Сабақ № 13		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқан оқушы саны:	Қатыспаған оқушы саны:
Сабақтың тақырыбы		Қисықсызықты трапеция және оның ауданы. Анықталған интеграл
Оқу бағдарламасына сәйкес оқыту мақсаттары		11.3.1.6 – қисықсызықты трапецияның анықтамасын білу және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолдану;
Сабақтың мақсаты:		интегралдауды дифференциалдауға кері процесс ретінде түсіну;
Сабақ барысы
Сабақтың кезеңі	Педагогтің әрекеті			Оқушының әрекеті	Бағалау	Ресурстар
Басы 5 минут	Ұйымдастыру сәті Бүгінгі сабақты Ұлы педагог Ушинскийдің мына сөзімен бастау: «Бір рет айтылған әңгіме артынан қайталануы керек. Бұл ұмытылғанды еске түсіру емес, қайта ұмытып кетуді болдырмау» Стартер: « Кім жылдам?» Кеспеқағаздарға тақырыпты қайталауға арналған сөйлемдер жазып, оларды жинақтау. (Презентация бойынша тексеру.)			Психологиялық ахуалға берілген тапсырманы орындайды.		Психологиялық ахуал.
Негізгі бөлім Тақырыпты ашу 10 минут	Жаңа тақырыпты ашу: қисықтарымен шектелгенфигурақисық сызықты трапеция деп аталады. Мысалы төмендегі сызбаларда түрлі қисық сызықты трапециялар берілген. 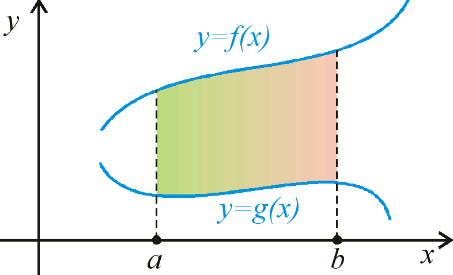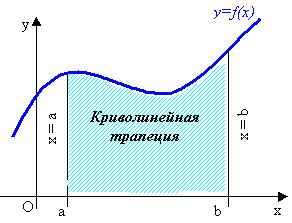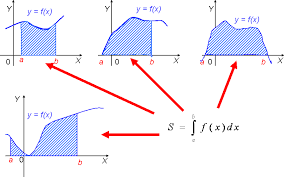Қарапайым трапецияның ауданы 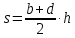екені белгілі Қисық сызықты трапецияның ауданын интегралды қолдану арқылы есептейміз. Егер болса, 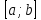аралығында берілген қисық сызықты трапецияның ауданы 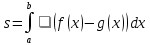формуласымен есептеледі.			« Жигсо» әдісі арқылы жаңа мәліметпен өз бетінше оқып танысады. Нақты анықтамаларға (+) белгісін қояып отырады. Оқушылар сұрақтарға жауап беріп, өзара ұжымдық талқылау жасағаннан кейін мұғалім оқушыларға сабақтың тақырыбы, мақсатымен таныстырады..		Үлестірмелі қағаздар 6-сынып математика оқулығы, карточка
Оқулықпен жұмыс 25 минут	1 - мысал: 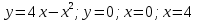сызықтарымен шектелген қисық сызықты трапецияның ауданын есептеңдер. 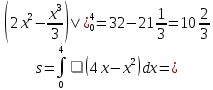(кв.бірлік) Жауабы: 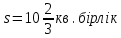2- мысал: 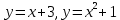сызықтарымен шектелген фигураның ауданын табыңдар. Шектерін табу үшін екі функцияның қиылысу нүктелерін есептейміз. 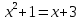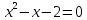Виет теоремасы бойынша 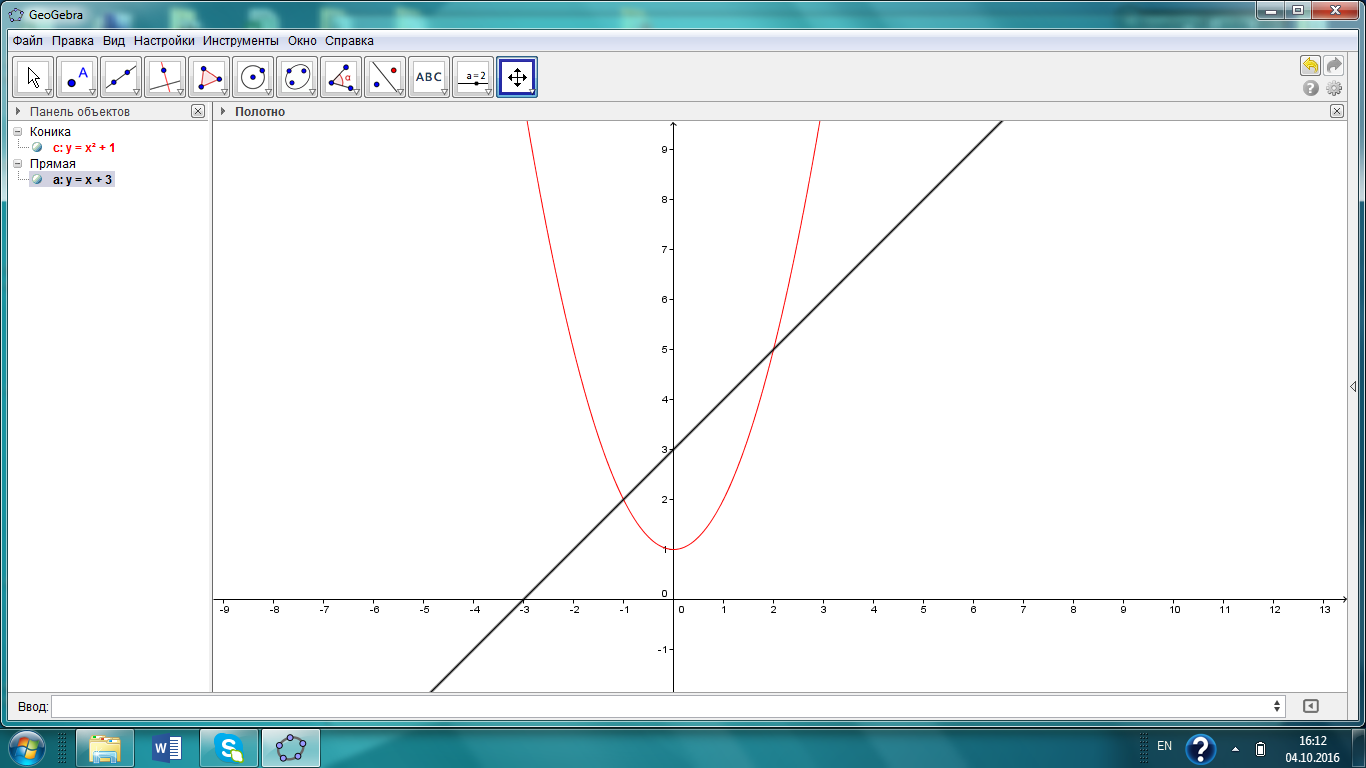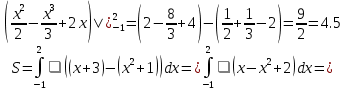(кв.бірлік) Жауабы:	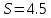	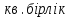	Дескриптор: дұрыс тұжырымды анықтайды; жауаптарын негіздейді. Дескриптор: - айнымалының мәндерін формулаға қояды; - мәнін есептейді; - көбейткішті түбір таңбасының алдына шығарады; - мәндерін сәйкестендіреді.	ҚБ: «Серпілген сауал» әдісі бойынша топтар бір бірін бағалайды. ҚБ: «Екі жұлдыз, бір тілек» арқылы жұптар бір-бірінің жұмысын бағалайды.	Топтық тапсырмалар.
Соңы 5 минут	Сабақты бекіту Рефлексия Үйге тапсырма:			Сабақты пысықтау тапсырмаларын орындау.
Кері байланыс	Рефлексия (жеке,жұпта,топта, ұжымда) «Бес саусақ» әдісі. Қағаз бетіне қолыңызды қойып, саусақтарыңызды айналдыра сызады. Әр саусақтың өзінің мәні бар, солар бойынша өз ойын білдіре отырып, жан-жақты қарастырады. 1. Бас бармақ – мен үшін маңызды және қызықты болды ...... 2. Сұқ саусақ – мен бүгін .......... түсіндім. 3. Ортаңғы саусақ – мен үшін ....... қиын болды. 4. Төртінші саусақ – менің бағам ....... , өйткені... 5. Шынашақ – Мен ............ білгім келеді			Оқушыларға «Бес саусақ» әдісі кері байланыс парағы таратылады. Оқушылар өздері белгілейді.	«СМС»	Кері байланыс парағы.

---

Смотрите также файлы

• Патологическая анатомия, понятие и учебный предмет. Её объекты исследования и методы познания.docx

• Фгбоу во уральский государственный университет физической культуры кафедра спортивной медицины и физической реабилитации.odt

• Контрольная работа по теме Силы в механике.doc

• ПЗ 7 Морфологические нормы русского литературного языка Теоретические вопросы.docx

• Этапы и основные черты русской философии.docx