Файл: 10сыныптаы алгебра жне анализ бастамалары курсын айталау.docx

Скачать файл (4,12Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 147

Скачиваний: 6

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Тапсырма

Сабақ № 24		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқан оқушы саны:	Қатыспаған оқушы саны:
Сабақтың тақырыбы		Жазық фигуралар аудандары мен айналу денелерінің көлемдерін анықталған интеграл көмегімен есептеу
Оқу бағдарламасына сәйкес оқыту мақсаттары		11.3.1.6 - берілген сызықтармен шектелген жазық фигураның ауданын есептеу;
Сабақтың мақсаты:		- Анықталған интегралдың көмегімен жазық фигуралардың ауданын есептеу үшін алғашқы функция формулаларын қолданып есептер шешу
Сабақ барысы
Сабақтың кезеңі	Педагогтің әрекеті			Оқушының әрекеті	Бағалау	Ресурстар
Басы 5 минут	Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту.			Психологиялық ахуалға берілген тапсырманы орындайды.		Психологиялық ахуал.
Негізгі бөлім Тақырыпты ашу 10 минут Оқулықпен жұмыс 25 минут	Есеп1. Парабола 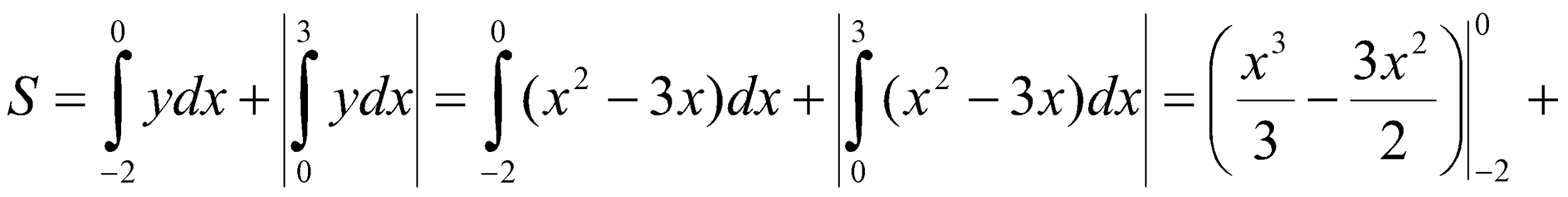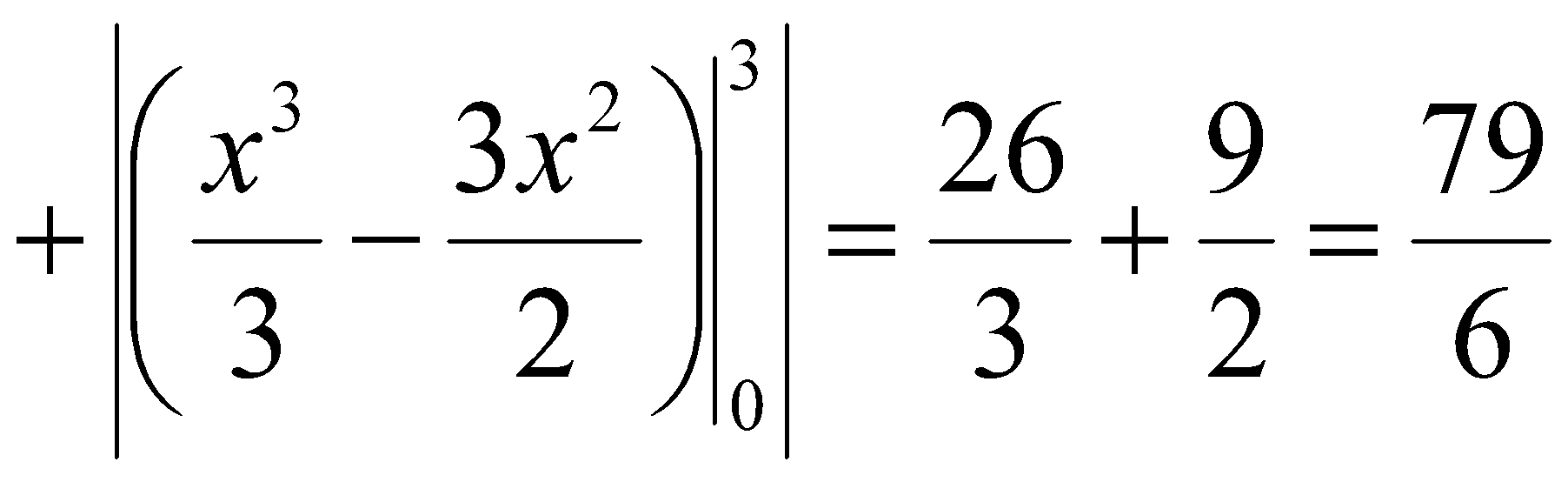түзу және өсімен шектелген фигураның ауданын табу керек (8-сурет). Шешу: параболасының өсімен қиылысу нүктелерінің абсциссаларын табамыз. Ол үшін деп ұйғарсақ, онан болып анықталады. (17) формуласы бойынша фигураның ауданы былай есептеледі: . Есеп2. Парабола және түзу мен шек-телген фигураның ауданын табу керек. Шешу: 9-суретте берілген фигура кескінделген. Ол жоғарыдан 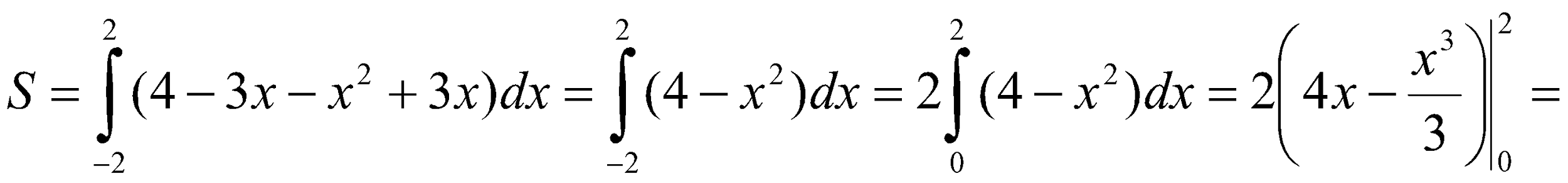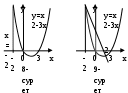түзуімен, төменнен парабола пен шектелген. (18) формуласы бойынша берілген фигураның ауданын есептеп табу үшін парабола мен түзудің қиылысу нүктелерінің абсциссала-рын білу керек. Олар теңдеулер жүйесі ; -ті біріктіріп шешкенде табылады. Жүйені шешсек, болып шығады. Демек, (18) формула бойынша болатынын көреміз.			«Бағдаршам» әдісі өткен материалды еске түсіру Дескриптор: - анықталған интеграл анықтамасын біледі - анықталған интеграл қасиеттерін қолданады - анықталған интегралды Ньютон-Лейбниц формуласымен есептейді; - қисықсызықты трапецияның ауданын табу үшін анықталған интегралды қолданады	Бағалау: Жұптар бірін – бірі бағалайды.	Үлестірмелі қағаздар
Соңы 5 минут	Сабақты бекіту Рефлексия Үйге тапсырма:			Сабақты пысықтау тапсырмаларын орындау.
Кері байланыс	Рефлексия (жеке,жұпта,топта, ұжымда) Сабақ соңында оқушылар рефлексия жүргізеді: «INSERT» әдісі I – interactive Мен нені бұрын білдім? N – nothing Мен нені білмедім? S – system Мен нені жаңа ғана үйрендім? E – effective Бұл қаншалықты тиімді? R – reading Маған тағы қандай ақпарат қажет? T – thinking Мен не туралы әлі ойлау керекпін?			Оқушыларға «INSERT» әдісі кері байланыс парағы таратылады. Оқушылар өздері белгілейді.	«INSERT» әдісі	Кері байланыс парағы.