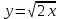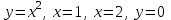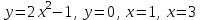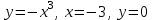Файл: 10сыныптаы алгебра жне анализ бастамалары курсын айталау.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 149
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Сабақ № 14 | Мектеп: | | ||||||
| Күні: | Мұғалімнің аты-жөні: | | ||||||
| Сынып: | Қатысқан оқушы саны: | Қатыспаған оқушы саны: | | |||||
| Сабақтың тақырыбы | Қисықсызықты трапеция және оның ауданы. Анықталған интеграл | | ||||||
| Оқу бағдарламасына сәйкес оқыту мақсаттары | 11.3.1.6 – қисықсызықты трапецияның анықтамасын білу және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолдану; | | ||||||
| Сабақтың мақсаты: | интегралдауды дифференциалдауға кері процесс ретінде түсіну; | | ||||||
| Сабақ барысы | | |||||||
| Сабақтың кезеңі | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | ||||
| Басы 5 минут | Ұйымдастыру сәті Бүгінгі сабақты Ұлы педагог Ушинскийдің мына сөзімен бастау: «Бір рет айтылған әңгіме артынан қайталануы керек. Бұл ұмытылғанды еске түсіру емес, қайта ұмытып кетуді болдырмау»
Кеспеқағаздарға тақырыпты қайталауға арналған сөйлемдер жазып, оларды жинақтау. (Презентация бойынша тексеру.) | Психологиялық ахуалға берілген тапсырманы орындайды. | | Психологиялық ахуал. | ||||
| Негізгі бөлім Тақырыпты ашу 10 минут | Қисық сызықты трапецияның ауданын интегралды қолдану арқылы есептейміз. Егер  болса, болса,  аралығында берілген қисық сызықты трапецияның ауданы аралығында берілген қисық сызықты трапецияның ауданы  формуласымен есептеледі. Оқушыларға Ох осімен және y=x-3, x=4, x=7 түзулерімен шектелген трапеция ауданын есептеуді ұсыныңыз. Төмендегі суреттен: 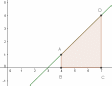 1-әдіс: 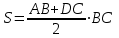 2-әдіс: F(x) - f(x) функциясының алғашқы функциясы екенін ескеріп 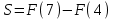 , мұндағы , мұндағы 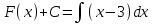 . .1-ші және 2-әдістерден алынған нәтижелерді салыстырыңыз және сәйкес қорытындылар жасаңыз. Егер f(x) функциясының графигі қисық сызық болса, онда жалпы жағдайда қисықсызықты трапеция деп, Ох осімен, x=a, x=b түзулерімен және f(x) функциясының графигімен шектелген фигураны айтады және ол келесі түрде болады: 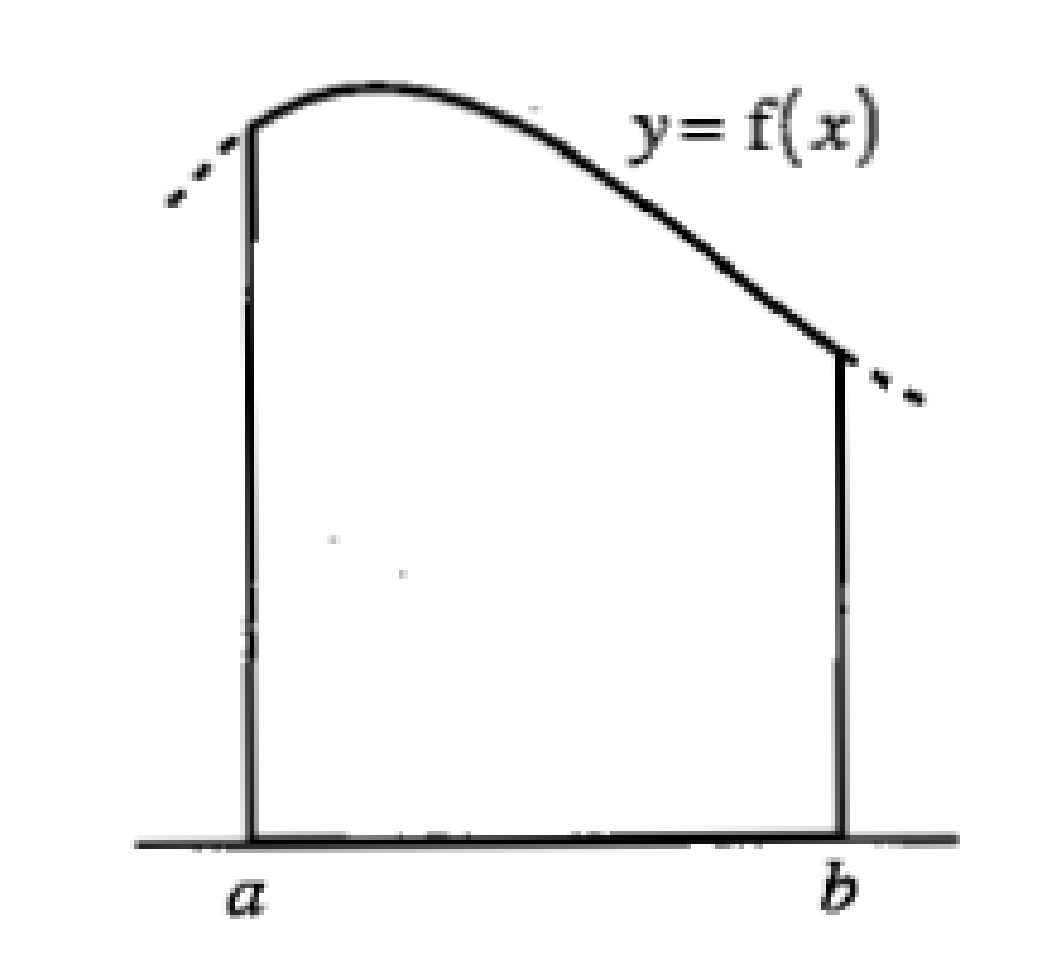 Әрі қарай оқушыларға келесідей қисықсызықты трапецияларды бейнелеуді ұсыныңыз: А деңгейі: f(x)=x2, x=1, x=3, В деңгейі: f(x)=sin(x), 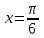 , , 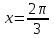 , , | « Жигсо» әдісі арқылы жаңа мәліметпен өз бетінше оқып танысады. Нақты анықтамаларға (+) белгісін қояып отырады. Оқушылар сұрақтарға жауап беріп, өзара ұжымдық талқылау жасағаннан кейін мұғалім оқушыларға сабақтың тақырыбы, мақсатымен таныстырады.. |  | Үлестірмелі қағаздар 6-сынып математика оқулығы, карточка | ||||
| Оқулықпен жұмыс 25 минут | 1 - мысал: 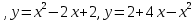 сызықтарымен шектелген фигураның ауданын табыңдар. 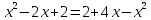 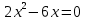 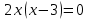 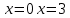 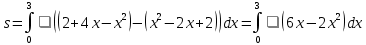 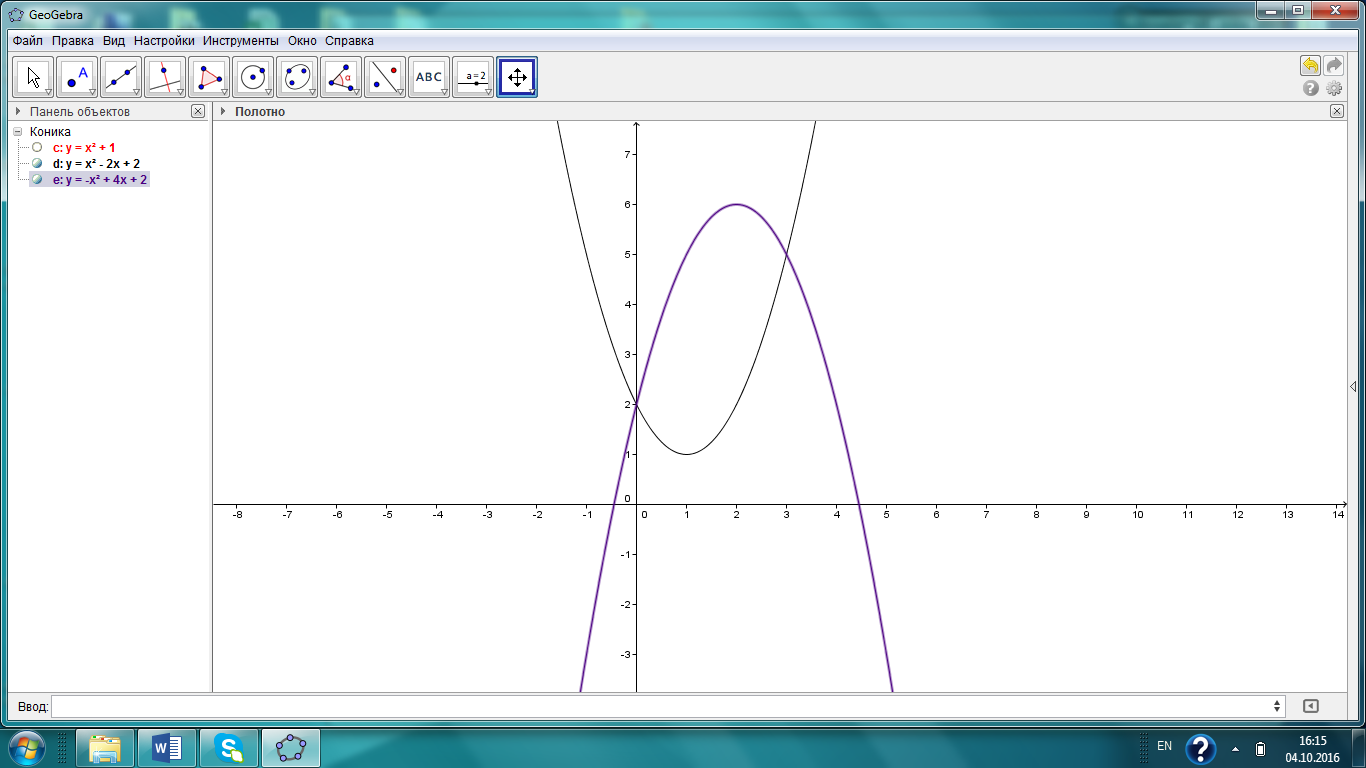 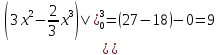 (кв.бірлік) (кв.бірлік)Жауабы: S= 9  Жеке жұмыс: А деңгейі. 1. Қисықсызықты трапецияның ауданын табыңыз, егер: 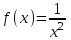 , a=2, b=5. , a=2, b=5.2. Қисықсызықты трапецияның ауданын табыңыз, егер: 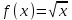 , a=1, b=4. , a=1, b=4.В деңгейі. Боялған фигуралардың аудандарын табыңыз: 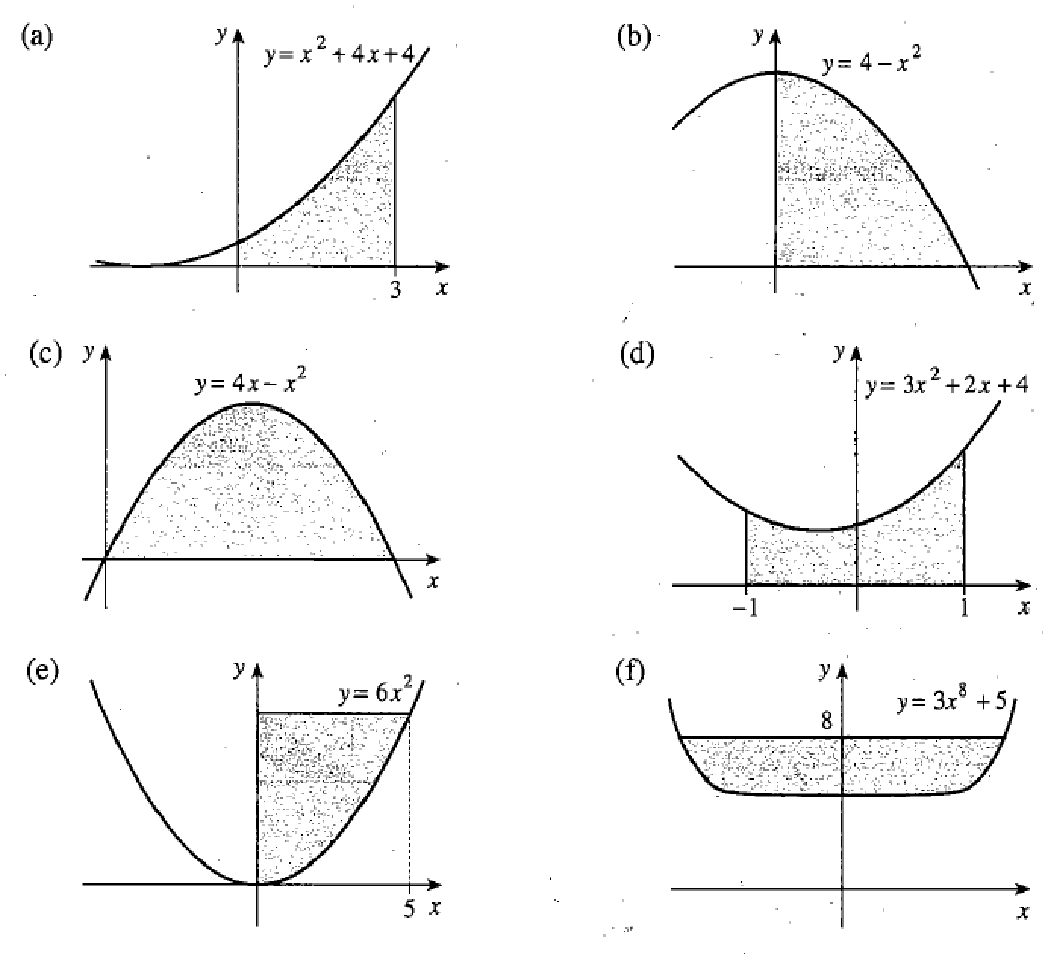 С деңгейі. 1. Суретте y=9x2 функциясының графигі кесінделген. Р нүктесінің координаталары - (4; 144). Боялған бөліктің ауданын табыңыз. 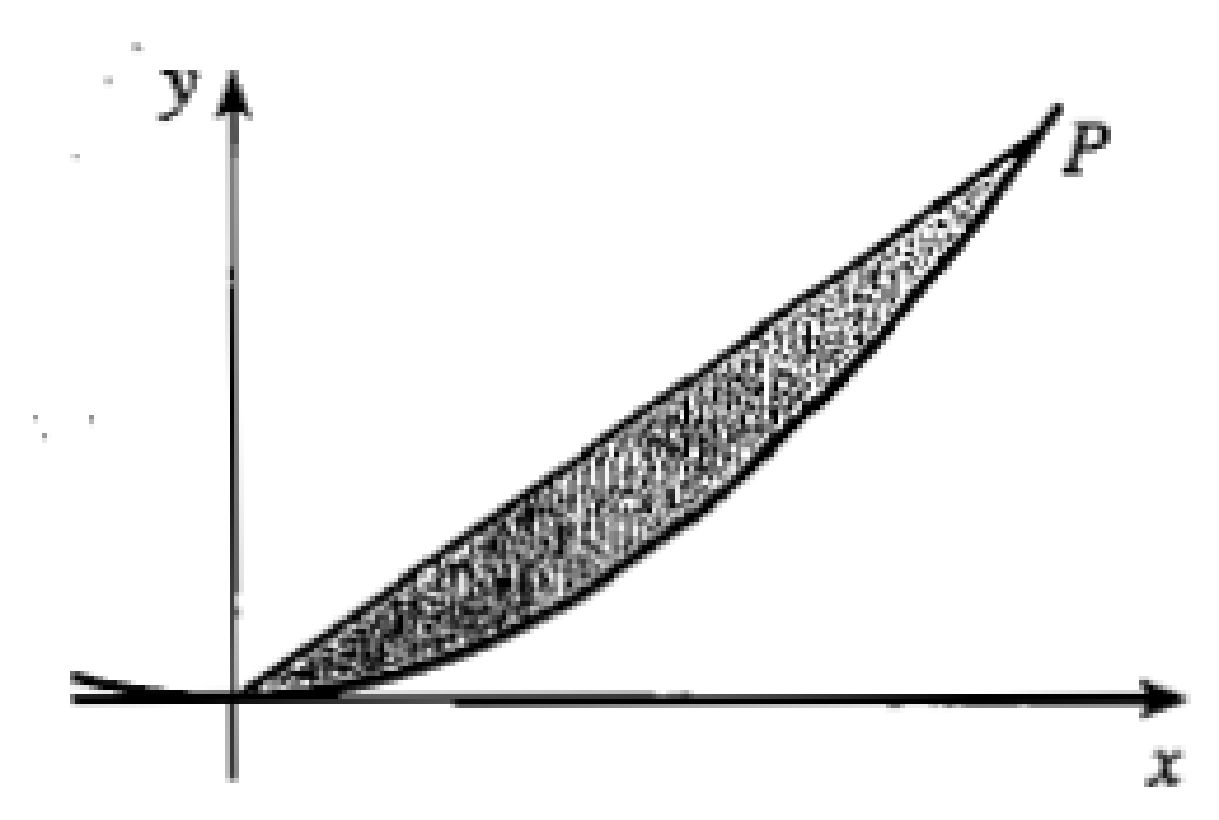 | Дескриптор:
Дескриптор: -берілген нүктеде функция графигіне жүргізілген нормаль және жанама теңдеуін табады; - функция графигі мен оның туындысының графигі (градиенті) арасындағы байланысты түсінеді; - функцияның экстремум нүктелерін табады; | ҚБ: «Серпілген сауал» әдісі бойынша топтар бір бірін бағалайды.  ҚБ: «Екі жұлдыз, бір тілек» арқылы жұптар бір-бірінің жұмысын бағалайды. | Топтық тапсырмалар. | ||||
| Соңы 5 минут | Сабақты бекіту Рефлексия Үйге тапсырма: | Сабақты пысықтау тапсырмаларын орындау. | | | ||||
| Кері байланыс | Рефлексия (жеке,жұпта,топта, ұжымда) «Бес саусақ» әдісі. Қағаз бетіне қолыңызды қойып, саусақтарыңызды айналдыра сызады. Әр саусақтың өзінің мәні бар, солар бойынша өз ойын білдіре отырып, жан-жақты қарастырады. 1. Бас бармақ – мен үшін маңызды және қызықты болды ...... 2. Сұқ саусақ – мен бүгін .......... түсіндім. 3. Ортаңғы саусақ – мен үшін ....... қиын болды. 4. Төртінші саусақ – менің бағам ....... , өйткені... 5. Шынашақ – Мен ............ білгім келеді | Оқушыларға «Бес саусақ» әдісі кері байланыс парағы таратылады. Оқушылар өздері белгілейді. | «СМС» | Кері байланыс парағы. | ||||
| Сабақ № 15 | Мектеп: | |||||
| Күні: | Мұғалімнің аты-жөні: | |||||
| Сынып: | Қатысқан оқушы саны: | Қатыспаған оқушы саны: | ||||
| Сабақтың тақырыбы | Қисықсызықты трапеция және оның ауданы. Анықталған интеграл | |||||
| Оқу бағдарламасына сәйкес оқыту мақсаттары | 11.3.1.6 – қисықсызықты трапецияның анықтамасын білу және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолдану; | |||||
| Сабақтың мақсаты: | интегралдауды дифференциалдауға кері процесс ретінде түсіну; | |||||
| Сабақ барысы | ||||||
| Сабақтың кезеңі | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | ||
| Басы 5 минут | Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. Практикада қабырғасы қисықсызық фигуралардың ауданын табу де кездеседі. Мұндай фигуралардың ауданын бізге белгілі формулалармен табу мүмкін емес. Анықтама. Үзіліссіз, теріс емес 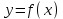 функциясының графигімен, ОХ осімен және х=а, х=b түзулерімен шектелген жазық фигура қисықсызықты трапеция деп аталады. функциясының графигімен, ОХ осімен және х=а, х=b түзулерімен шектелген жазық фигура қисықсызықты трапеция деп аталады. | Психологиялық ахуалға берілген тапсырманы орындайды. | Бағалау: Тапсырманы мұғалім нұсқауына сүйене отырып тақтада орындайды. Мадақтау | Психологиялық ахуал. | ||
| Негізгі бөлім Тақырыпты ашу 10 минут | 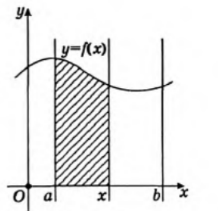 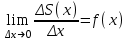 . Бұдан . Бұдан 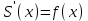 екені шығады, яғни екені шығады, яғни 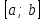 кесіндісінде S(х) функциясы кесіндісінде S(х) функциясы 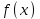 функциясы үшін алғашқы функция болып табылады. Егер функциясы үшін алғашқы функция болып табылады. Егер 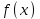 функциясы үшін алғашқы функциялардың бірін функциясы үшін алғашқы функциялардың бірін 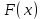 деп белгілесек, онда деп белгілесек, онда 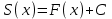 Мұндағы С- кез келген сан. С- ның мәнін табу үшін х- тің орнына а- қоямыз. Сонда 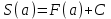 және және 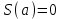 , олай болса, , олай болса, 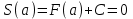 , , 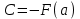 . Демек, . Демек, 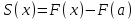 .Қисықсызықты трапецияның ауданы .Қисықсызықты трапецияның ауданы 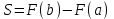 ( | | | Үлестірмелі қағаздар | ||
| Оқулықпен жұмыс 25 минут | Мысал 1 x=2 , x=3, у=0 және  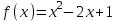 сызықтарымен шектелген қисықсызықты трапецияның ауданын табыңыз. сызықтарымен шектелген қисықсызықты трапецияның ауданын табыңыз. Алдымен параболаның графигін саламыз. Содан кейін x=2 , x=3 түзулерін саламыз. 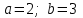 . . 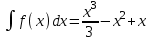 +С +С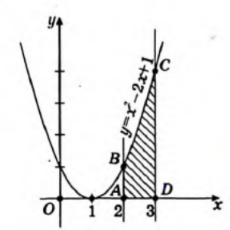 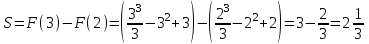 Жауабы: 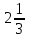 Мысал 2 Абцисса осімен және 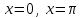 түзулері түзулері 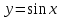 функциясының графигімен шектелген қисықсызықты трапецияның ауданын есептейік. функциясының графигімен шектелген қисықсызықты трапецияның ауданын есептейік. Шешуі: 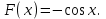 Ал Ал 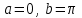 . Онда . Онда 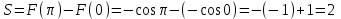 Жауабы: 2кв.бірл. | Дескриптор:
 | ҚБ: «Екі жұлдыз, бір тілек» әдісі арқылы оқушылар өз- өзін бағалайды | Топтық тапсырмалар. | ||
| Соңы 5 минут | Сабақты бекіту Рефлексия Үйге тапсырма: | Сабақты пысықтау тапсырмаларын орындау. | | | ||
| Кері байланыс | Рефлексия (жеке,жұпта,топта, ұжымда) «Бес саусақ» әдісі. Қағаз бетіне қолыңызды қойып, саусақтарыңызды айналдыра сызады. Әр саусақтың өзінің мәні бар, солар бойынша өз ойын білдіре отырып, жан-жақты қарастырады. 1. Бас бармақ – мен үшін маңызды және қызықты болды ...... 2. Сұқ саусақ – мен бүгін .......... түсіндім. 3. Ортаңғы саусақ – мен үшін ....... қиын болды. 4. Төртінші саусақ – менің бағам ....... , өйткені... 5. Шынашақ – Мен ............ білгім келеді | Оқушыларға «Бес саусақ» әдісі кері байланыс парағы таратылады. Оқушылар өздері белгілейді. | «СМС» | Кері байланыс парағы. | ||
| Сабақ № 16 | Мектеп: | |||||
| Күні: | Мұғалімнің аты-жөні: | |||||
| Сынып: | Қатысқан оқушы саны: | Қатыспаған оқушы саны: | ||||
| Сабақтың тақырыбы | Қисықсызықты трапеция және оның ауданы. Анықталған интеграл | |||||
| Оқу бағдарламасына сәйкес оқыту мақсаттары | 11.3.1.6 – қисықсызықты трапецияның анықтамасын білу және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолдану; | |||||
| Сабақтың мақсаты: | интегралдауды дифференциалдауға кері процесс ретінде түсіну; | |||||
| Сабақ барысы | ||||||
| Сабақтың кезеңі | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | ||
| Басы 5 минут | Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. Қисықсызықты трапецияның ауданын қалай табамыз? 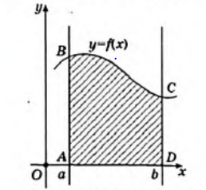 Суретте кескінделген қисықсызықты трапецияның ауданы S деп белгілейік. Егер  кесіндісіне тиісті х нүктесін алсақ, онда S(х) функциясы х=а түзуімен және кесіндісіне тиісті х нүктесін алсақ, онда S(х) функциясы х=а түзуімен және 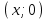 нүктесі арқылы өтетін абцисса осіне перпендикуляр түзумен шектелген қисықсызықты трапецияның ауданын көрсетеді. нүктесі арқылы өтетін абцисса осіне перпендикуляр түзумен шектелген қисықсызықты трапецияның ауданын көрсетеді. | Психологиялық ахуалға берілген тапсырманы орындайды. | Бағалау: Тапсырманы мұғалім нұсқауына сүйене отырып тақтада орындайды. Мадақтау | Психологиялық ахуал. | ||
| Негізгі бөлім Тақырыпты ашу 10 минут | Қисықсызықты трапецияның ауданын табу үшін келесі алгоритм қолданылады.
( | | | Үлестірмелі қағаздар | ||
| Оқулықпен жұмыс 25 минут | Сыныппен жұмыс.
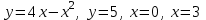 Жауабы: 6
Жауабы: 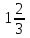
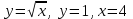 Жауабы: 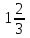 Жұппен жұмыс Негізгі деңгей Мына сызықтармен шектелген фигураның ауданын табыңыз Орта деңгей 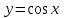 функциясының графигімен және функциясының графигімен және 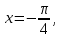 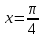 түзулерімен шектелген фигураның ауданын табыңыз түзулерімен шектелген фигураның ауданын табыңыз Шығармашылық деңгей Егер 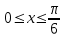 болса, онда болса, онда 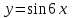 және және 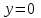 қисықтарымен шектелген фигураның ауданы неге тең? қисықтарымен шектелген фигураның ауданы неге тең?Жеке жұмыс Мына сызықтармен шектелген фигураның ауданын табыңыз 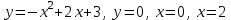 | Дескриптор:
Дескриптор:
| Бағалау: Тапсырманы мұғалім нұсқауына сүйене отырып тақтада орындайды. Мадақтау. Бағалау. Жұптар бір- бірін карусель әдісі бойынша бағалайды. | Топтық тапсырмалар. | ||
| Соңы 5 минут | Сабақты бекіту Рефлексия Үйге тапсырма: | Сабақты пысықтау тапсырмаларын орындау. | | | ||
| Кері байланыс | Рефлексия (жеке,жұпта,топта, ұжымда) «Бес саусақ» әдісі. Қағаз бетіне қолыңызды қойып, саусақтарыңызды айналдыра сызады. Әр саусақтың өзінің мәні бар, солар бойынша өз ойын білдіре отырып, жан-жақты қарастырады. 1. Бас бармақ – мен үшін маңызды және қызықты болды ...... 2. Сұқ саусақ – мен бүгін .......... түсіндім. 3. Ортаңғы саусақ – мен үшін ....... қиын болды. 4. Төртінші саусақ – менің бағам ....... , өйткені... 5. Шынашақ – Мен ............ білгім келеді | Оқушыларға «Бес саусақ» әдісі кері байланыс парағы таратылады. Оқушылар өздері белгілейді. | «СМС» | Кері байланыс парағы. | ||
| Сабақ № 17 | Мектеп: | ||||||||||||||||||||||||
| Күні: | Мұғалімнің аты-жөні: | ||||||||||||||||||||||||
| Сынып: | Қатысқан оқушы саны: | Қатыспаған оқушы саны: | |||||||||||||||||||||||
| Сабақтың тақырыбы | Қисықсызықты трапеция және оның ауданы. Анықталған интеграл | ||||||||||||||||||||||||
| Оқу бағдарламасына сәйкес оқыту мақсаттары | 11.3.1.4 Қисық сызықты трапецияның анықтамасын біледі және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолданады 11.3.1.5 анықталған интеграл ұғымын біледі, анықталған интегралды есептей алады; | ||||||||||||||||||||||||
| Сабақтың мақсаты: | - анықталған интеграл анықтамасын біледі - анықталған интеграл қасиеттерін қолданады - анықталған интегралды Ньютон-Лейбниц формуласымен есептейді; - қисықсызықты трапецияның ауданын табу үшін анықталған интегралды қолданады. | ||||||||||||||||||||||||
| Сабақ барысы | |||||||||||||||||||||||||
| Сабақтың кезеңі | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | | ||||||||||||||||||||
| Басы 5 минут | Ұйымдастыру сәті Жүректен-жүрекке» оқушыларды жылы жүзбен қарсы алу, амандасу, жылы лебіздер айту. «Бағдаршам» әдісі өткен материалды еске түсіру мақсатында тест түрінде өткізіледі. Әр оқушының қолына бағдаршам тәріздес сигналдық карта ретінде беріледі. Оқушылар тапсырманы орындап, дұрыс жауапқа сәйкес түсті көтереді. Оқушылар бір-бірінен сұрамай, үндемей өздері орындауы тиіс. Оқушылар қате орындаған тапсырма болса, бірден сол тапсырманы тақтада талдап, кері байланыс беріледі. №1 Анықталған интегралды есепте 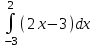
 №2 Анықталған интегралды есепте №2 Анықталған интегралды есепте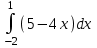
 №3 Анықталған интегралды есепте №3 Анықталған интегралды есепте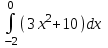
Шешімі: №1 Қызыл №2 Сары №3 Сары | Психологиялық ахуалға берілген тапсырманы орындайды. «Бағдаршам» әдісі өткен материалды еске түсіру | | Психологиялық ахуал. | | ||||||||||||||||||||
| Негізгі бөлім Тақырыпты ашу 10 минут Оқулықпен жұмыс 25 минут | Жұптық жұмыс Интерактивті оқыту әдісі «Сағат бойынша достасу» Әрбір оқушыға сағат суреті бар қағаз таратылады. Әр оқушы белгіленген уақытың ішінде сағат 12.00, 15-00, 18.-00 бен 20.00-де кездесетін оқушыны анықтап, есімін сол уақыттын тұсына жазып қояды. Уақыт айтылған сайын оқушы уақытқа сай кездесетін адамын таңдайды.Әр уақытта жұптарға тапсырма беріліп, жұптар ой бөліседі.Сонда әр оқушы бірнеше оқушылармен диалогқа қатысып, әртүрлі тапсырмалар орындайды. 12.00 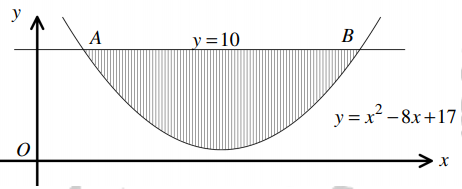 а) Екі қисықтың қиылысу А мен В нүктелердің координаталарын табыңдар. ә) берілген қисықтармен шектелген фигураның ауданын есептеңдер Жауабы: а) 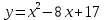 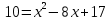 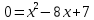 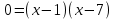 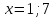 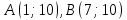 ә) 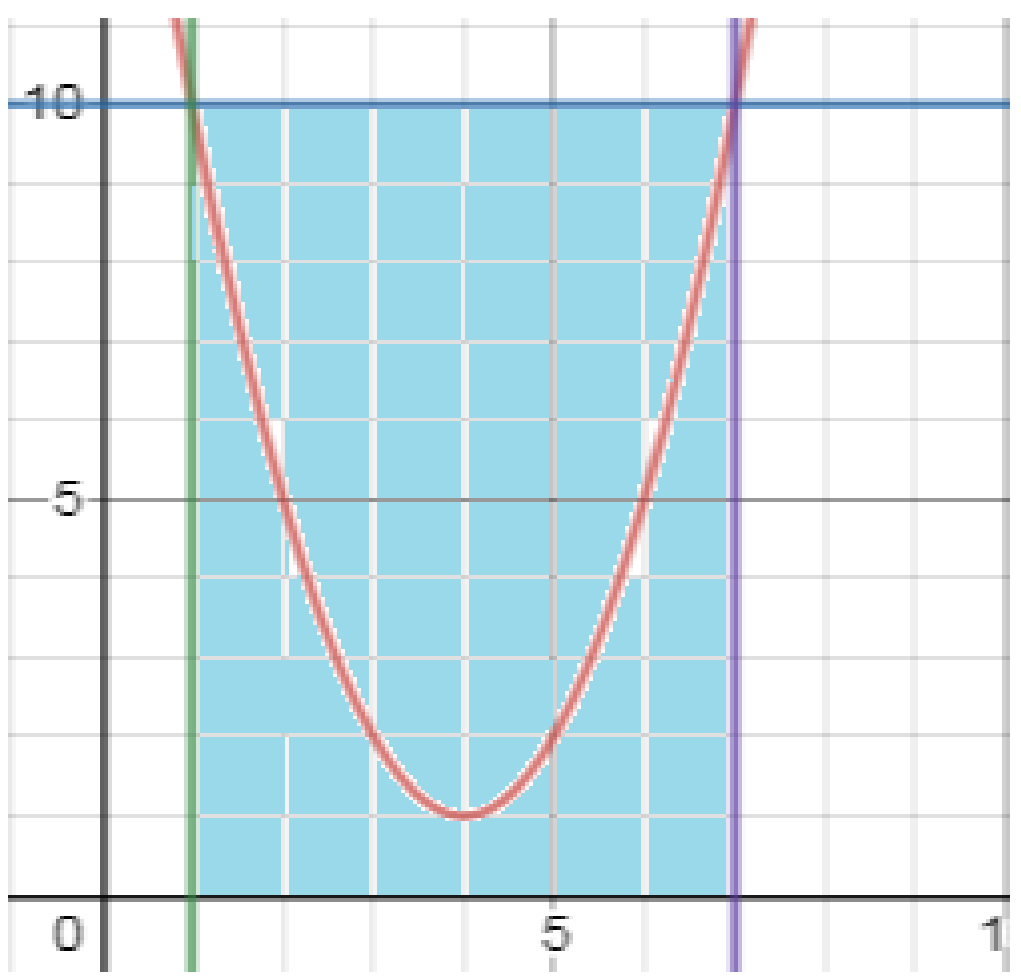 сурет 1 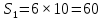 (кв.бірлік) (кв.бірлік)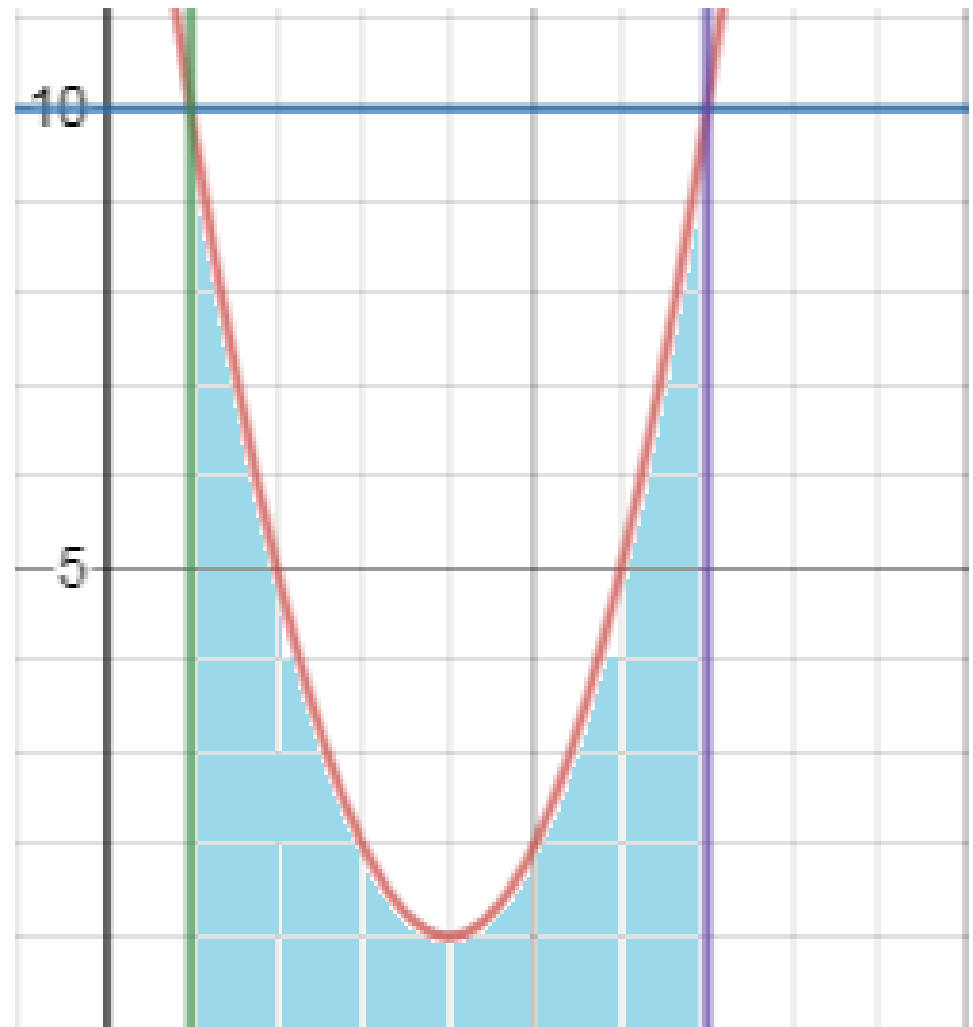 Сурет 2 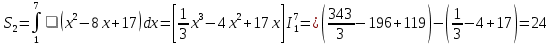 (кв.бірлік) (кв.бірлік)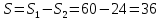 (кв.бірлік) (кв.бірлік)15.00 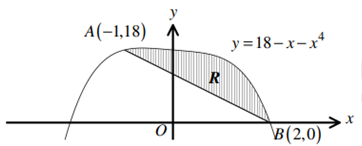 Сурет 3 Жоғарыдағы суретте теңдеуі 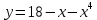 қисық сызығы және координат осьтерін қисық сызығы және координат осьтерін 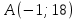 бен бен 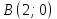 нүктелерінде қиятын түзу сызығы берілген. Екі қисықтың қиылысуынан пайда болған бөліктің ауданын табыңдар. нүктелерінде қиятын түзу сызығы берілген. Екі қисықтың қиылысуынан пайда болған бөліктің ауданын табыңдар.Жауабы:  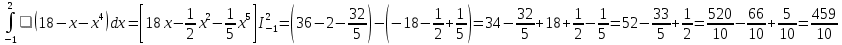  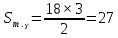 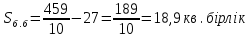 18.00 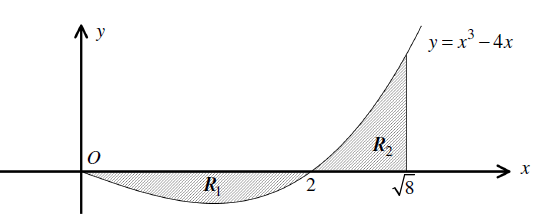 Жоғарыда теңдеуі 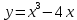 кубтық қисығы берілген. кубтық қисығы берілген.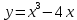 , , 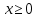 Қисық сызық координат жүйесіндегі х осін бас нүктеден мен x = 2 нүктелерінде қиып өтеді. 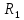 фигурасы фигурасы 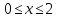 аралығында, ал аралығында, ал 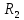 фигурасы фигурасы 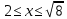 шектелген. шектелген. 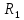 және және 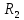 фигураларының аудандары тең екенін көрсетіңдер фигураларының аудандары тең екенін көрсетіңдерШешімі: 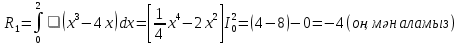 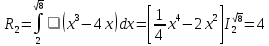 (кв.бірлік) (кв.бірлік) |
||||||||||||||||||||||||
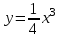 және
және