Построить функцию распределения с.в.Х. Найти закон распределения и числовые характеристики с.в. Y = X².

6. 
   Ошибки прибора распределены нормально мат.ожиданием 2 и ско, равным 4. Какова вероятность того, что ошибка превзойдет 6? Какова вероятность того, что это произойдет хотя бы два раза из пяти измерений?
   

.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.112

1. 
   На пяти карточках написаны цифры: 1, 2, 3, 4, 5. Две из них, одна за другой, вынимаются. Найти вероятность того, что число на второй карточке будет больше, чем на первой.
   

2. 
   В ящике находятся однотипные изделия, изготовленные раз­ными заводами; из них
   1   2   3   4   5   6   7   8

---

а изделий изготовлены заводом I, bизделий —заводом II, с изделий — заводом III. Из ящика вынимают одно за другим все находящиеся в нем изделия и отмечают места их изготовления. Найти Вероятность того, что при этом изделие завода I появится раньше, чем изделие завода II.

3. 
   Завод изготовляет изделия, каждое из которых с вероятностью r (независимо от других) оказывается дефектным. При осмотре дефект, если он имеется обнаруживается с вероятностью р. Для контроля из продукции завода выбирается n изделий. Вся контролируемая партия браку­ется, если в выборке будет обнаружено не менее четырех дефект­ных. Найти вероятность того, что вся контролируемая партия будет забракована.
   

4. 
   Группа студентов состоит из а отличников, Ь хорошо успеваю­щих и с занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие сту­денты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность события А = {студент получит хорошую или отличную оценку}.
   

5. 
   Есть четыре кубика с цифрами на гранях 1,2,..., 6 и одна правильная пирамида с цифрами на гранях 1,2,3,4. Наугад выбрали предмет и бросили. Выпала цифра 4. Какова вероятность того, что бросали кубик?
   

6. 
   Дана функция распределения случайной величины Х
   

Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х три раза попадет в интервал (0,25;1).

7. 
   Отклонение размера детали от номинала подчинено нормальному закону с m=0 и σ=0,12мм. Если отклонение ‌‌‌ Δх ‌ < 0,02 , то деталь годится для изделия №1. Если не годится для изделия №1, но отклонение в пределах –0,1< Δх < 0,03, то для изделия №2 . Какова вероятность того, что деталь нельзя будет использовать? Какова вероятность того, что деталь подойдет только для изделия №2?
   

---

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.113

1. 
   Имеется М операторов и N > М перенумерованных приборов, ко­торые они могут обслуживать. Каждый оператор выбирает случайным образом и с одинаковой вероятностью любой прибор, но с условием, что ни один прибор не может обслуживаться больше, чем одним опера­тором. Найти Вероятность того, что будут выбраны для обслужива­ния приборы с номерами 1, 2, ..., М.
   

2. 
   Первый прибор состоит из п₁ узлов, второй из п₂узлов. Каж­дый прибор работал в течение времени t. За это время каждый узел первого прибора выходит из строя, независимо от других, с вероятностью q₁второго — с Вероятностью q₂. Найти Вероятность того, что за время tв первом приборе выйдет из строя т₁узлов, а во втором — m₂ узлов.
   

3. 
   Оцените вероятность того, что четырехзначный номер первой встречной машины а) не содержит четных цифр; б) содержит две или более пятерки.
   

4. 
   Анализ крови в 90% случаев диагностирует некоторое заболевание. В 4% случаев ошибочно находим болезнь у здорового человека. Известно, что 10% людей имеют это заболевание. Какова вероятность, что человек, получивший положительный результат анализа, действительно болен?
   

5. 
   Дана функция распределения случайной величины Х
   

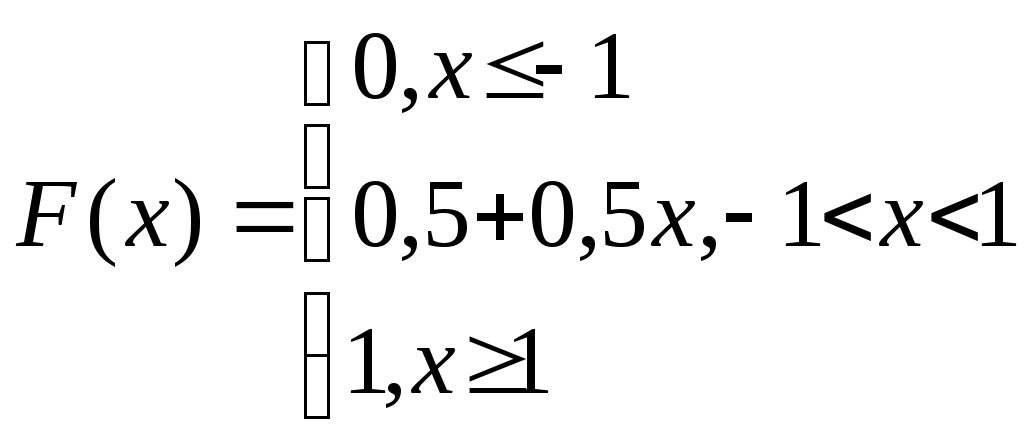Найти плотность распределения, числовые характеристики. Найти вероятность P{X≤0,75}, P{-0,5≤X≤0,5}.

6. 
   В кузове 768 арбузов. Каждый может оказаться неспелым с вероятностью 0,15. С какой вероятностью число спелых арбузов в партии лежит в пределах от 600 до 670?
   

7. 
   Батарея произвела 6 выстрелов по объекту. Вероятность попадания при одном выстреле равна 0,3. Найти наивероятнейшее число попаданий. Найти вероятность разрушения объекта, если для этого достаточно двух попаданий.
   

---

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.

Вар.114

1. 
   В шкафу находятся девять однотипных приборов. В начале опыта все они новые (ни разу не бывшие в эксплуатации). Для времен­ной эксплуатации берут наугад три прибора; после эксплуатации их возвращают в шкаф. На вид прибор, бывший в эксплуатации, не отличается от нового. Найти вероятность события
   

А — {после трехкратного выбора и эксплуатации не останется новых приборов}.

2. 
   Прибор состоит из двух дублирующих друг друга узлов I и II и может случайным образом работать в одном из двух режимов: благоприятном и неблагоприятном. В благоприятном режи­ме надежность каждого узла равна р₁в неблагоприятном р₂. Вероятность того, что прибор будет работать в благоприятном режиме, равна Р_б , в неблагоприятном 1 — Р_б . Найти полную (среднюю) надежность прибора Р.
   

3. 
   Вероятность хотя бы одного попадания при 4-х независимых выстрелах равна 0,9984. Найти вероятность попадания при одном выстреле.
   

4. 
   Два стрелка по очереди стреляют по бутылке. У каждого по два патрона. Первый попадает с вероятностью 0,4 , а второй - 0,6. Найти математическое ожидание и с.к.о. числа израсходованных патронов.
   

5. 
   Дана функция распределения случайной величины Х
   

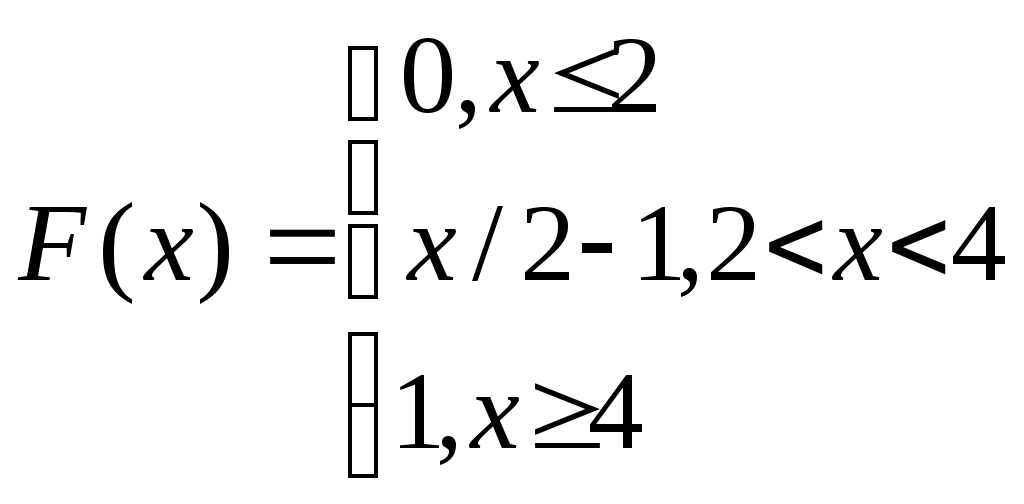Найти плотность распределения, числовые характеристики. Найти вероятность P{X≥13/4}.

6. 
   Станок-автомат изготавливает валики, диаметр которых Х есть нормальная случайная величина с m=10мм и =0,15мм. найти вероятность того, что диаметр окажется меньше 10,07мм. Найти диапазон равных отклонений от математического ожидания, в котором с вероятностью 0,9973 будут находиться диаметры изготовленных валиков.
   

7. 
   Студент знает 7 вопросов из 10. Наугад вытягивает 3. Найти закон распределения и числовые характеристики с.в. Х – число известных вопросов среди взятых.
   

---

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.

Вар.115

1. 
   Прибор состоит из четырех узлов — первого, второго, треть­его и четвертого, которые за время т работы прибора могут независи­мо друг от друга выходить из строя. Надежность (Вероятность безот­казной работы) i-ro узла равна p_i; Вероятность отказа q_i= 1 — р_i (i= 1, 2, 3, 4). Найти вероятности следующих событий:
   

А - {все узлы работают безотказно};

В - {первый узел отказал, остальные нет};

С - {один из узлов отказал, другие нет};

D- {отказало ровно два узла из четырех};

Е - {отказало не менее двух узлов};

Р -.{отказал хотя бы один узел}.

2. 
   Монета бросается т раз. Найти вероятность того, что герб появится не менее kраз и не более l раз (k≤ l ≤ т).
   

3. 
   В шкафу стоят однотипные приборы, из которых а новых и Ь уже бывших в эксплуатации (а >2, Ь > 2). Выбираются наугад два прибора и эксплуатируются в течение какого-то времени, после чего возвращаются в шкаф. Затем вторично выбираются наугад два при­бора. Найти вероятность события А = {оба вторично выбранных при­бора — новые}.
   

4. 
   Автобусы идут с интервалом 7 минут. Предполагая, что время ожидания распределено равномерно в этом интервале, найти функцию распределения времени ожидания и вероятность того, что ждать придется не менее двух минут. Чему равна дисперсия времени ожидания?
   

5. 
   Из трех урн вынимают по одному шару. В первой урне находятся три белых и два черных шара. Во второй — два белых и три черных шара. Третья урна содержит три белых и три черных шара. Если известно, что два из трех вынутых шаров белые, то какова вероятность, что белый шар был вынут из первой урны?
   

---

Смотрите также файлы

• Существенным фактором для любой хорошо функционирующей социальной системы являются социальная защита, социальная и экономическая поддержка населения.docx

• 1 Теоретические и методические аспекты анализы прибыли и ее налогообложения.docx

• Начальник пожарной части Зам начальника пожарной части Старшина части.docx

• Законе рф О защите прав потребителей.docx

• Тема Функции и методы, структура и документы стандартизации.docx