ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 539
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В семье 5 детей. Найти вероятность того, что среди детей два мальчика; не более двух мальчиков; более двух мальчиков; не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
В первом ящике 5 годных и 7 дефектных деталей, а во втором 9 годных и 3 дефектные. Детали смешивают и извлекают наугад две. Они оказались дефектными. Какова вероятность того, что они из второго ящика?
Производится стрельба по цели до первого попадания. На стрельбу отпущено 4 снаряда. Вероятность попадания при одном выстреле 0,4. Попадания независимы. Найти математическое ожидание числа израсходованных снарядов.
Время жизни микроба распределено по показательному закону с плотностью
f(t)=μe-μt, где1/μ – среднее время жизни микроба, равное 8 часов. Какова вероятность того, что микроб проживет более 12 часов? Какова вероятность того, что он умрет в возрасте от 5 до 8 часов?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.81
В шкафу 10 пар ботинок различных цветов. Наугад берем четыре. Какова вероятность того, что среди выбранных не будет парных?
Из полной колоды карт (52 листа) извлекается одна. Рассмотрим события : A – появление туза; B – появление красной масти; C – появление бубнового туза; D – появлений десятки.
Какие из пар этих событий зависимы?
Два стрелка по очереди стреляют по мишени до первого попадания. У них по 5 патронов. Вероятности попадания у первого стрелка 0,2, а у второго – 0,3. Найти вероятность того, что первый сделает больше выстрелов.
Завод отправил на базу 500 приборов. Вероятность повреждения прибора в пути равна 0,002. Найти вероятность повреждения а) ровно одного; б) менее трех; в) хотя бы трех.
Производится n независимых выстрелов по цистерне с горючим, Каждый снаряд попадает с вероятностью p. Если попал один снаряд, то цистерна воспламеняется с вероятностью p1, если попало два или более снарядов, то наверняка загорится. Известно, что цистерна загорелась. Какова вероятность того, что попал один снаряд?
Бросаем две правильные пирамидки, на гранях которых написаны цифры 1,2,3,4. Найти закон распределения суммы выпавших цифр.
По 15 независимым измерениям посчитано среднее арифметическое скорости 424,7 м/с. Определить 95%-й доверительный интервал для ожидаемой скорости, если прибор имеет нормальную ошибку с с.к.о. , равной 7м/с. Систематической ошибки нет.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 82
Вероятность одного попадания в цель при залпе из двух орудий равна 0,38. Какова вероятность поражения цели первым орудием, если известно, что для второго орудия эта вероятность равна 0,8 ?
Среди 30 экзаменационных билетов есть 20 легких. Каким по очереди Вам выгоднее тянуть билет первым, вторым, третьим и т.д.?
Оцените вероятность того, что четырехзначный номер первой встречной машины не содержит а) цифры 5; б) содержит две и более пятерки.
В кузове 768 арбузов. Каждый может оказаться неспелым с вероятностью 0,25. С какой вероятностью число спелых арбузов в партии лежит в пределах от 564 до 600? Более 700?
Третья часть только одной из трех партий является второсортной. Деталь, взятая из какой-то партии, оказалась первосортной. Какова вероятность того, что она из партии, в которой есть второсортные?
По некоторой цели производится стрельба пятью ракетами. Вероятность попадания у каждой ракеты 0,7. Найти числовые характеристики случайной величины Х – число попаданий.
Рост человека в данной местности есть нормальная с.в. с m=165 и =7. Какова вероятность того, что наудачу выбранный человек имеет рост от 155 до 170 см? Выше, чем 182 см?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 83
Производится стрельба по плоской прямоугольной мишени ( |х| ≤2 и |у| ≤ 1 ).
Известно, что произошло попадание и оно равновероятно в любой точке мишени.
Найти вероятности событий: А – абсцисса точки попадания не меньше ординаты,
В – произведение координат точки неотрицательно,
С – сумма абсолютных величин координат больше единицы.
Наугад набираем шестизначный телефонный номер. Какова вероятность того, что все цифры окажутся различными?
Сколько раз нужно бросить игральную кость, чтобы с вероятностью не меньше а) 0.5; б) 0.9 хотя бы один раз выпала шестерка
Есть четыре кубика с цифрами на гранях 1,2,..., 6 и одна правильная пирамида с цифрами на гранях 1,2,3,4. Наугад выбрали предмет и бросили. Выпала цифра 4. Какова вероятность того, что взяли кубик?
В урне 5 белых и 22 черных шаров. Вынули 3 шара. Случайная величина Х – число вынутых белых шаров. Построить функцию распределения величины X.
Случайная величина Xраспределена по «закону прямоуголь ного треугольника» в интервале (0, а) (см. рис.). 1) Написать выражение плотности f (х); 2) найти функцию распределения F (х); 3) найти вероятность попадания случайной величины Xна участок от а/2 до а; 4) найти числовые характеристики величины X:
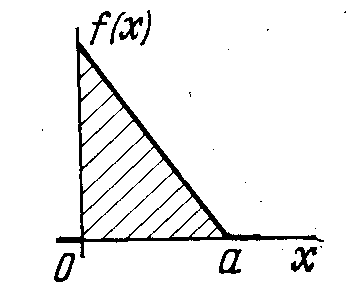
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 84
Вероятность одного попадания в цель при залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8.
В урне 9 белых и 4 черных шара. Извлекаем 3 шара. Какова вероятность того, что третий будет черным? Какова вероятность того, что третий будет черным, если известно, что первые два разные?
Из пачки в десять билетов выигрышными являются два. Наугад вынимаем 5 билетов. Какова вероятность того, что среди них 1 выигрышный? То же, но при возвращении каждого билета обратно в пачку и перемешивании.
Оцените вероятность того, что четырехзначный номер первой встречной машины не содержит а) цифры 5; б) содержит две и более пятерки.
В кузове 768 арбузов. Каждый может оказаться неспелым с вероятностью 0,25. С какой вероятностью число спелых арбузов в партии лежит в пределах от 564 до 600?
На полку выставляем случайно 5 книг. Определить случайную величину – «место конкретной книги, считая слева направо». Найти закон распределения и числовые характеристики.
Ошибки прибора распределены нормально с нулевым мат.ожиданием и ско, равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того,
что это произойдет лишь три раза в пяти измерениях?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 85
Случайная точка равномерно распределена внутри квадрата со стороной, равной а . Найти вероятность того, что расстояние от центра квадрата до точки меньше а/2.
Двое бросают монету по очереди. Выигрывает тот, у кого раньше появится герб. Найти вероятности выигрыша каждого из игроков.
Из колоды в 52 карты последовательно извлекают 4. Найти вероятность того, что они будут разных мастей. Вероятность того, что будет хотя бы один туз. Вероятность того, что ровно 2 из них будут пиковым.
В первом ящике 5 годных и 7 дефектных деталей, а во втором 9 годных и 3 дефектные. Детали смешивают и извлекают наугад две. Они оказались дефектными. Какова вероятность того, что они из второго ящика?
Две игральные кости бросают до выпадения «шестерки» хотя бы на одной из них. Найти закон распределения и числовые характеристики случайной величины Y – число бросков до появления «шестерки»
Произведено 16 измерений начальной скорости снаряда. Результаты измерений (в м/с) следующие: 1235.6; 1237.5; 1232.9; 1236.2; 1238.5; 1234.2; 1235.9; 1233.3; 1234.5; 1236.8; 1237.6; 1233.1; 1234.3; 1237.5; 1235.4; 1234.7. Вычислить оценки математического ожидания и дисперсии начальной скорости снаряда. Построить 95%-ый доверительный интервал для математического ожидания скорости.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 86
Наугад выбираем два числа из интервала [ 0 , 1 ]. Какова вероятность того, что их произведение более 0,2 ?
Бросаем 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков. Какова вероятность разных очков на всех костях?
Из колоды в 52 карты последовательно извлекают 4. Найти вероятность того, что они будут разных мастей. Вероятность того, что все будут красной масти. Вероятность того, что ровно 2 из них будут пиковым.
Бросаем две игральные кости. Какова вероятность того, что сумма очков более шести? Какова вероятность того, что модуль разности очков равен 1?
Третья часть только одной из трех партий является второсортной. Деталь, взятая из какой-то партии, оказалась первосортной. Какова вероятность того, что она из партии, в которой есть второсортные?
По некоторой цели производится стрельба пятью ракетами. Вероятность попадания у каждой ракеты 0,7. Найти числовые характеристики случайной величины Х – число попаданий.
Сколько нужно произвести измерений, чтобы модуль ошибки измерения был не более 8 с вероятностью 0,9, если с.к.о. измерений известно и равно = 12 ? Ошибки нормальны.
То же, но при доверительной вероятности 0,99 ?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 87
На девяти карточках написаны цифры: 0, 1,2, 3, 4, 5, 6, 7, 8. Две из них вынимаются наугад и укладываются на стол в порядке появления, затем читается полученное число, например 07 (семь), 14 (четырнадцать) и т. п. Найти Вероятность того, что число будет четным.
Имеются два ящика, содержащих типовые элементы замены (ТЭЗ). В первом ящике а исправных ТЭЗ и bнеисправных; во втором — с исправных и dнеисправных. Из каждого ящика наугад вынимается по одному ТЭЗ. Найти Вероятность того, что оба ТЭЗ будут исправными. Найти вероятность того, что оба вынутых ТЭЗ будут неисправны.
При въезде в новую квартиру в осветительную сеть было включено 2kновых электролампочек. Каждая лампочка в течение года перегорает с вероятностью p. Найти вероятность события А = {в течение года не менее половины первоначально включенных лампочек придется заменить новыми}.
Цех производит изделия; любое из них с вероятностью р имеет дефект. Каждое изделие осматривается браковщиком, который обнаруживает дефект, если он имеется, с Вероятностью