Файл: Урок Прямая и отрезок.docx

Урок 1. Прямая и отрезок

Цель деятельности учителя	Создать условия для систематизации знаний о взаимном расположении точек и прямых, ознакомления учащихся со свойством прямой (через любые две точки можно провести прямую и притом только одну), рассмотрения приема практического проведения прямых на плоскости (провешивание)
Термины и понятия	Отрезок, прямая, точка, плоскость
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления		Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют находить в различных источниках информацию, необходимую для решения математических проблем. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Геометрия. 7–9 классы: учеб. для общеобразоват. организаций / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. М.: Просвещение, 2014*. • Задания для фронтальной и самостоятельной работы. • Сведения из истории возникновения и развития науки геометрии

---

I этап. Вводная беседа
Цель деятельности	Совместная деятельность
Познакомить с предметом «геометрия»	(Ф/И) Учитель рассказывает о науке «геометрия»; учащиеся слушают, задают уточняющие вопросы (см. Ресурсный материал)
II этап. Учебно-познавательная деятельность. Изучение нового материала
Цель деятельности	Совместная деятельность
Ввести основные понятия геометрии и основную символику	(Ф/И) К доске для выполнения заданий вызывается по одному учащемуся, остальные работают в тетрадях. Учитель читает задание и по мере необходимости вводит новые понятия, символы, делает необходимые записи на доске. 1) Начертите прямую. Как ее можно обозначить? (Прямая а или АВ.) Рис. 1 2) Отметьте точку С, не лежащую на данной прямой, и точки D, Е, K, лежащие на прямой. 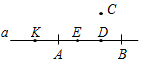Рис. 2 – В математике существуют специальные символы, позволяющие кратко записать какое-либо утверждение. Символы  и  означают соответственно «принадлежит» и «не принадлежит» и называются символами принадлежности. 3) Используя символы принадлежности, запишите предложение «Точка D принадлежит прямой АВ, а точка С не принадлежит прямой а». (D  АВ, С  а.) 4) Используя рисунок и символы  и , запишите, какие точки принадлежат прямой b, а какие – нет. (F, В, А, С  b; K, Е, N  b.) 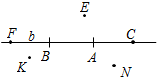Рис. 3 – Сколько прямых можно провести через заданную точку А? (Через заданную точку А можно провести множество прямых.) – Сколько прямых можно провести через две точки? (Одну прямую.) – Через любые две точки можно провести прямую? (Да.) – Итак, через любые две точки можно провести прямую и притом только одну. Это утверждение назовем свойством прямой. 5) Начертите прямые XY и МK, пересекающиеся в точке О. 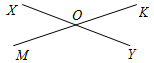Рис. 4 – Для того чтобы кратко записать, что прямые ХY и МK пересекаются в точке О, используют символ  и записывают так: XYМK = О. – Сколько общих точек может быть у двух прямых? (Две прямые могут иметь или одну общую точку, или ни одной общей точки.) 6) На прямой а отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки. (Получились отрезки АВ, ВС, CD, AC, AD, BD.) Рис. 5
III этап. Выполнение практических заданий
Цель деятельности	Совместная деятельность
Выявить уровень сформированности практических навыков учащихся	(Ф/И) 1. Выполнение практических заданий № 2, 3 на с. 7 учебника. 2. Вопросы к учащимся: – Могут ли прямые ОА и АВ быть различными, если точка О лежит на прямой АВ? (Прямые ОА и АВ не могут быть различными, так как обе они проходят через точки А и О, а через две точки проходит только одна прямая.) – Даны две прямые а и b, пересекающиеся в точке С, и точка D, отличная от точки С и лежащая на прямой а. Может ли точка D лежать на прямой b? (Точка D не может лежать на прямой b, так как две прямые не могут иметь двух общих точек.) 3. Введение понятия отрезка (используется рис. 7 учебника). 4. Самостоятельное выполнение учащимися задания № 5. 5. Изложение материала п. 2 «Провешивание прямой на местности» в виде беседы (по рис. 8 и 9 учебника)
IV этап. Самостоятельная работа
Цель деятельности	Совместная деятельность
Выявить уровень сформированности теоретических знаний и практических умений учащихся	(И) Самостоятельная работа проводится в форме диктанта на листках и сдается на проверку учителю. 1. Начертите прямую и обозначьте ее буквой b. 1) Отметьте точку М, лежащую на прямой b. 2) Отметьте точку D, не лежащую на прямой b. 3) Используя символы  и , запишите предложение: «Точка М лежит на прямой b, а точка D не лежит на ней». 2. Начертите прямые а и b, пересекающиеся в точке K. На прямой а отметьте точку С, отличную от точки K. 1) Являются ли прямые KС и а различными прямыми? Ответ обоснуйте. 2) Может ли прямая b проходить через точку С? Ответ обоснуйте. 3*. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки. 4*. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки
V этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Что изучает предмет «геометрия»? – Когда он появился? – Зачем он нужен?		(И) Домашнее задание: пункты 1, 2; ответить на вопросы 1–6 на с. 25 учебника; практические задания № 4, 6, 7

---

Ресурсный материал

Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название связано с применением геометрии для измерений на местности. Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, проводить дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических знаний. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические представления, которые формировались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории. Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и т. д., то есть то, что на современном геометрическом языке называется движением. Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем рассуждений, доказательств.

Попытки греческих ученых привести геометрические факты в систему начинаются уже в V в. до н. э. Наибольшее влияние на все последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III в. до н. э. Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения и геометрия впервые была представлена как математическая наука. Работа содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней подведен итог предшествующему развитию греческой математики и создан фундамент для дальнейшего развития этой науки. Книга была переведена на множество языков, а геометрия, изложенная в ней, стала называться

---

евклидовой геометрией.



Сведения о самом Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III веке до н. э. Евклид – первый математик александрийской школы, автор работ по астрономии, оптике, музыке и др. Из других его сочинений по математике стоит отметить работу «О делении фигур», сохранившуюся в арабском переводе, четыре книги «Конические сечения», материал которых вошел в произведение с таким же названием АполлонияПергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Филона Александрийского.

В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и обращая внимание только на форму и размеры предметов, мы приходим к понятию геометрической фигуры.

На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы и с такими фигурами, как треугольник, прямоугольник, круг (продемонстрировать модели фигур).

Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.

Школьный курс геометрии делится на планиметрию и стереометрию. Такие фигуры, как отрезок, луч, прямая, угол, окружность, круг, треугольник, прямоугольник, являются плоскими, то есть целиком укладываются на плоскости. Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией (от латинского слова «планум» – плоскостьи греческого «метрео» – измеряю). В стереометрии изучаются свойства фигур в пространстве, таких как параллелепипед, шар, цилиндр, пирамида (продемонстрировать модели). Мы начнем изучение геометрии с планиметрии.

Урок 2. Луч и угол

Цель деятельности учителя	Создать условия для актуализации знаний учащихся о том, что такое луч и угол, введения на наглядном уровне понятий внутренней и внешней областей неразвернутого угла, ознакомления с различными обозначениями лучей и углов
Термины и понятия	Отрезок, прямая, точка, плоскость, луч, угол, внутренняя область угла, внешняя область угла
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления		Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют находить в различных источниках информацию, необходимую для решения математических проблем. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для фронтальной работы

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать теоретические знания учащихся по предыдущей теме	(Ф/И) 1. Проверить правильность выполнения домашнего задания. Для этого к доске вызвать двоих учащихся, которые представляют свои решения. 2. Сообщить итоги математического диктанта
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Ввести понятия угла и луча	(Ф/И) 1. Введение понятия луча (использовать рис. 11 учебника). 2. Обозначение луча (рис. 12 а и б). 3. Выполнение практических заданий: 1) Проведите прямую а. а) Отметьте на ней точки А, В и С так, чтобы точка А лежала между точками В и С. б) Назовите лучи, исходящие из точки А. в) Отметьте на луче АВ точку D. 2) Укажите все лучи, изображенные на рисунке: а) исходящие из точек М и D; б) составляющие вместе с их общим началом одну прямую. 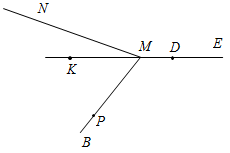4. Самостоятельное выполнение практического задания № 8. 5. Объяснение темы «Угол». 1) На модели показывается, из каких элементов состоит данная фигура. 2) Дается определение угла. 3) Вводятся различные способы обозначения угла. 4) Вводятся понятия развернутого и неразвернутого угла (рис. 15 а и б)
III этап. Решение задач
Деятельность учителя	Совместная деятельность
Совершенствовать навыки решения задач	(Ф/И) 1. Выполнение практических заданий № 9, 10 и 11 на доске и в тетрадях. 2. Выполнение заданий: 1) Начертить неразвернутый угол hk, заштриховать его внутреннюю область, провести луч l, исходящий из вершины и проходящий внутри этого угла, то есть луч, разделяющий угол hkна два угла: hlиlk. (Работа по рис. 16а.) Учащиеся делают вывод, что если угол hk развернутый, то любой луч, исходящий из его вершины и не совпадающий с лучами h и k, также делит этот угол на два угла (рис. 16б). 2) Выполнить практическое задание № 14. 3) Устно решить задания № 15, 16 (по рис. 17) и задание № 17 (по рис. 18)
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какая геометрическая фигура называется углом? – Из каких элементов он состоит? – Составьте синквейн к уроку		(И) Домашнее задание: изучить пункты 3, 4 из § 2; ответить на вопросы 4–6 на с. 25 учебника; выполнить практические задания № 12–13

---