ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 191
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.3.Фильтры, согласованные с шумоподобными сигналами.
Согласованные фильтры обычно используются для оптимального приема шумоподобных сигналов (ШПС). Аналоговый фильтр, согласованный с ШПС содержит: 1. Линию задержки с отводами; количество отводов равно количеству импульсов, время движения импульса от одного до другого отвода равно длительности импульса; 2. Фазовращатели (+, -); фазовращатель со знаком "+" не меняет, а со знаком "-" меняет знак входного импульса на противоположный; чередование знаков фазовращателей совпадает с зеркальным отображением чередования знаков в сигнале. 3.Сумматор; 4.Фильтр согласованный с одиночным прямоугольным импульсом (ФСОИ).
Билет 19
38.
1.Амплитудный модулятор. Расчет СМХ амплитудного модулятора методом кратных дуг.
Схема базового амплитудного модулятора имеет вид:















 C L
C L 


 Uнч(t) UАМ(t)
Uнч(t) UАМ(t)



 Uвч(t)
Uвч(t)  E Ek
E Ek


На входе 3 напряжения:
1.
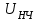 - модулирующее напряжение.
- модулирующее напряжение.2.
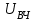 - несущее напряжение.
- несущее напряжение.3.
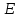 - напряжение смещения.
- напряжение смещения.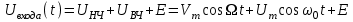 (7.6)
(7.6)Транзистор – нелинейный элемент. Он преобразует спектр входного процесса, чтобы получить нужные нам частоты (несущую и 2 боковых)
LC-контур (линейная электрическая цепь) выделяет нужные частоты.
Определим спектр тока на выходе транзистора, если ВАХ транзистора аппроксимируется полиномом второй степени.
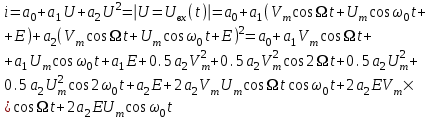
Построим спектр входного напряжения:

 Uвх Um
Uвх Um
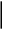 E Vm
E Vm  0 0
0 0 В соответствии с расчетом построим и спектр тока
iчерез транзистор:


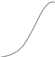
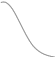 i
iРис.7.7.


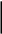


 0 2 0- 0 0+ 20
0 2 0- 0 0+ 20 Резонансный контур настроен на
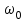 и выделяет частоты
и выделяет частоты 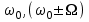 .
.Сопротивление резонансного контура имеет вид:
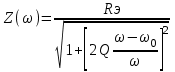 (7.7)
(7.7)АЧХ контура показана на рис.7.7 пунктиром.
На контуре выделяются токи с частотами
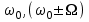 . Для каждой из этих частот резонансный контур имеет свое сопротивление. Умножив амплитуду соответствующей составляющей тока на сопротивление контура для этой частоты , получим амплитуду составляющей напряжения на контуре. В целом, мы получим на контуре АМ сигнол:
. Для каждой из этих частот резонансный контур имеет свое сопротивление. Умножив амплитуду соответствующей составляющей тока на сопротивление контура для этой частоты , получим амплитуду составляющей напряжения на контуре. В целом, мы получим на контуре АМ сигнол: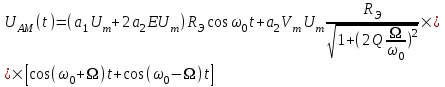
1-ое слагаемое – несущая частота АМ сигнала.
2-ое слагаемое – боковые частоты АМ сигнала.
Спектр напряжения на контуре представляет собой спектр АМ сигнала, рассмотренный нами выше.
СМХ
СМХ – это зависимость амплитуды 1-ой гармоники выходного тока I1 модулятора от напряжения смещения E при амплитуде вч несущей Um=const и амплитуде нч модулирующего сигнала Vm = 0.
2.АЦП и ЦАП.
Непрерывные (аналоговые) сигналы
могут принимать в любой момент времени сколь угодно близкие друг другу значения. Пример непрерывного сигнала - гармоническое колебание. На рисунке 2.1 отмечен уровень 0,7 вольт. Но данный сигнал принимает значения и 0,71 вольт, и 0,701 вольт, т.е. значения, сколь угодно близкие к 0.7 в.
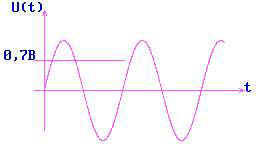
Рис.2.1
Дискретные сигналы принимают в определенные (тактовые) моменты времени определенные значения, отличающиеся одно от другого на конкретную величину. Пример дискретного сигнала - двоичный (бинарный) сигнал. Он принимает только два значения 0 и 1 (рис.2.2.).
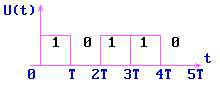
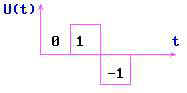
В общем случае дискретный сигнал может принимать m значений (m-ичный сигнал). На следующем рис.2.3 приведена временная диаграмма троичного сигнала (он может принимать три значения: 0, +1, -1).
Сигнал ИКМ - это двоичный сигнал, однозначно соответствующий исходному аналоговому сигналу. Устройство, преобразующее аналоговый сигнал в цифровой, называют аналого-цифровым преобразователем (АЦП).
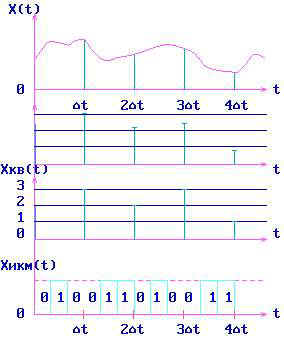
Рассмотрим процесс формирования сигнала ИКМ по рис. 2.4.
Переход от непрерывного сигнала к сигналу ИКМ включает три основные операции:
-
Дискретизация исходного непрерывного сигнала х(t), показанного на рис.2.4.а в соответствии с теоремой Котельникова; интервал дискретизации равен:
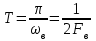 , (2.1)
, (2.1)если ωв=2πFв - ширина спектра исходного сигнала. В результате дискретизации получим сигнал хд(t), показанный на рис.2.4.б.
2) Квантование по уровню импульсов-отсчетов. Диапазон допустимых значений x(t) разбивается на разрешенные уровни – уровни квантования. Операция квантования состоит в том, что вместо истинного значения амплитуды импульса передается ближайший разрешенный уровень. Пусть уровни квантования 0,1,2,3 и т.д. вольт. Тогда вместо 0,2 вольт передаем 0; вместо 1,4 вольт - 1 вольт и т.д. В результате квантования получим сигнал х
кв(t), показанный на рис.2.4.в.
а
 )
)а)
Хд(t)
б)
в)
г)
Рис.2.4.
3) Кодирование квантованных импульсов - отсчетов. Кодирование состоит в том, что вместо квантованного уровня передается комбинация кодовых символов. Если код – двоичный, то символами кода являются 1 и 0. Количество различных символов, которые образуют кодовые комбинации, называется основанием кода m. Количество символов в кодовой комбинации называется длиной кодовой комбинации n. Общее количество кодовых комбинаций равно N=mn . Примитивное кодирование состоит в том, что номер уровня квантования записывается двоичным числом, т.е. в виде двоичной кодовой комбинации (m=2). Предположим, что комбинация состоит из трех импульсов n=3. Тогда десятичным номерам уровней соответствуют следующие двоичные числа:
0=000, 1 = 001; 2 = 010; 3 = 011; 4 = 100; 5=101; 6=110; 7=111.
В результате кодирования мы получили двоичный сигнал ИКМ хИКМ(t) на рис.2.4.г, однозначно соответствующий исходному непрерывному сигналу х(t) с заданной точностью.
Сигнал ИКМ передается в линию связи и поступает на вход приемника. Для восстановления на приемной стороне исходного непрерывного сигнала выполняются следующие операции:
-
Декодирование принятых кодовых комбинаций; т.е. принятая двоичная комбинация превращается в соответствующее десятичное число: 000 превращается в 0 вольт, 001 в 1 вольт, 010 в 2 вольта, 011 в 3 вольта ….и т.д. 111 в 7 вольт. -
Полученные импульсы – отсчеты подаются на вход восстанавливающего фильтра, который теоретически должен быть идеальным фильтром нижних частот (ИФНЧ).
На выходе этого ИФНЧ получим с заданной точностью исходный непрерывный сигнал
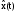 . Среднеквадратическая погрешность восстановленного сигнала
. Среднеквадратическая погрешность восстановленного сигнала 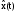 относительно x(t) должна быть не более заданной величины. Устройство, преобразующее цифровой сигнал в аналоговый, называют
относительно x(t) должна быть не более заданной величины. Устройство, преобразующее цифровой сигнал в аналоговый, называют