Файл: Задание 3 Произведем расчет числа групп 4.doc

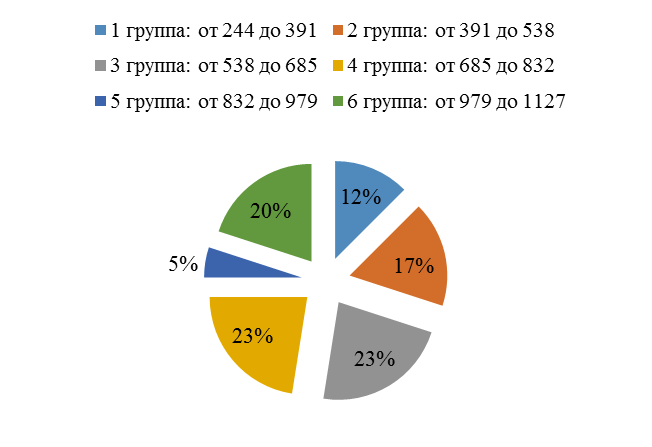
Отметим, что наибольшее количество предприятий по группам у 3 и 4 группы которые составили по 23% от общего количества предприятий.
Проранжируем ряд. Для этого сортируем его значения по возрастанию.
Таблица для расчета показателей.

x	|x - xср|	(x-xср)2
244	449.4	201960.36
362	331.4	109825.96
364	329.4	108504.36
372	321.4	103297.96
373	320.4	102656.16
416	277.4	76950.76
426	267.4	71502.76
429	264.4	69907.36
479	214.4	45967.36
495	198.4	39362.56
498	195.4	38181.16
526	167.4	28022.76
539	154.4	23839.36
618	75.4	5685.16
623	70.4	4956.16
631	62.4	3893.76
639	54.4	2959.36
646	47.4	2246.76
653	40.4	1632.16
657	36.4	1324.96
673	20.4	416.16
702	8.6	73.96
713	19.6	384.16
726	32.6	1062.76
738	44.6	1989.16
754	60.6	3672.36
763	69.6	4844.16
780	86.6	7499.56
789	95.6	9139.36
820	126.6	16027.56
856	162.6	26438.76
878	184.6	34077.16
988	294.6	86789.16
1002	308.6	95233.96
1024	330.6	109296.36
1062	368.6	135865.96
1106	412.6	170238.76
1120	426.6	181987.56
1125	431.6	186278.56
1127	433.6	188008.96
27736	7796.8	2302001.6

---

Для оценки ряда распределения найдем следующие показатели:

Показатели центра распределения.

Простая средняя арифметическая


Мода.

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.

Мода отсутствует (имеются несколько показателей с одинаковым значением частоты).

Медиана.

Медиана - значение признака, которое делит единицы ранжированного ряда на две части. Медиана соответствует варианту, стоящему в середине ранжированного ряда.

Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных.

Находим середину ранжированного ряда:

h = ^f/₂ = ⁴⁰/₂ =20.

Ранжированный ряд включает четное число единиц, следовательно, медиана определяется как средняя из двух центральных значений:

(657 + 673)/2 = 665

В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (x_ср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом:

3(x_ср-Me) ≈ x_ср-Mo

Квартили.

Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q₁, 25% будут заключены между Q₁ и Q₂, 25% - между Q₂ и Q₃. Остальные 25% превосходят Q₃.

Находим ¹/₄ ранжированного ряда:

h = ⁿ/₄

---

 = ⁴⁰/₄ = 10.

Ранжированный ряд включает четное число единиц, следовательно квартиль Q₁ определяется как среднее из двух значений: (495 + 498)/2 = 496.5

Находим ³/₄ ранжированного ряда:

h = ³ⁿ/₄ = ^3*40/₄ = 30. Q₃ = (820 + 856)/2 = 838
Показатели вариации.

Абсолютные показатели вариации.

Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.

R = x_max - x_min = 1127 - 244 = 883

Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.



Каждое значение ряда отличается от другого в среднем на 194.92

Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).



Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).



Среднее квадратическое отклонение.



Каждое значение ряда отличается от среднего значения 693.4 в среднем на 239.896

Оценка среднеквадратического отклонения.



Относительные показатели вариации.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.

Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

---

Поскольку v>30% ,но v<70%, то вариация умеренная.

Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.



Каждое значение ряда отличается от среднего значения 693.4 в среднем на 239.896.

Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная.

---

Задание 1.2.

Для изучения тесноты связи между производительностью труда и стоимостью промышленно-производственных фондов вычислите коэффициент Спирмена. Сделайте выводы.
Вычислим коэффициент Спирмена

№п/п	Производительность труда		Стоимость промышленно-производственных фондов		Квадрат разности рангов d2=(Rx-Ry)2
	ч	Ранг Rx	млн.руб.	Ранг Ry
1	1,36	25	479	9	256
2	1,31	22	673	21	1
3	1,28	21	713	23	4
4	0,81	8	1120	38	900
5	1,18	17	726	24	49
6	1,38	26	1127	40	196
7	0,41	2	498	11	81
8	0,92	9	763	27	324
9	1,09	14	1106	37	529
10	1,34	23	789	29	36
11	0,34	1	416	6	25
12	1,84	37	495	10	729
13	1,35	24	426	7	289
14	1,25	19	362	2	289
15	1,02	12	646	18	36
16	1,41	28	631	16	144
17	1,08	13	988	33	400
18	0,43	3	364	3	0
19	1,19	18	1062	36	324
20	0,51	4	639	17	169
21	1,27	20	623	15	25
22	1,15	15	657	20	25
23	0,70	6	618	14	64
24	0,58	5	820	30	625
25	1,43	29	856	31	4
26	0,74	7	1125	39	1024
27	1,49	30	429	8	484
28	1,79	36	878	32	16
29	2,08	40	780	28	144
30	1,96	39	653	19	400
31	1,53	31	702	22	81
32	1,88	38	526	12	676
33	0,98	11	373	5	36
34	1,68	34	1002	34	0
35	1,65	33	539	13	400
36	1,78	35	1024	35	0
37	0,93	10	738	25	225
38	1,38	26	244	1	625
39	1,56	32	754	26	36
40	1,17	16	372	4	144
Итого	х		х		9 815
Среднее	1,23		693,4

---