Файл: Задание 3 Произведем расчет числа групп 4.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 35

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Задание 1.2.

Задание 2.1.

Задание 2.2.

Список источников



Рассчитываем коэффициент Спирмена:

1 - (6 * 9815) / (40 * 1599) = 0,0793

Р = 0,0793 => теснота связи между производительностью труда и стоимостью промышленно-производственных фондов прямая и слабая.

Проверяем значимость полученных результатов по t-критерию Стьюдента:

.
При уровне значимости 5%, tТ (0,05,38) = 2,02.

Следовательно, значимость результатов не подтверждается т.к. .

Задание 2.1.


По исходным данным проведите корреляционно-регрессионный анализ влияния на производительность труда (выработки продукции на 1 работающего) количества переработанной свеклы. Опишите результаты, сделайте выводы.
Проведем корреляционно-регрессионный анализ влияния на производительность труда количества переработанной свеклы.


№ п/п
Производительность труда, ч
Количество переработанной свеклы, тыс.т.
ху
х2
у2

1
1,36
1220
1659,2
1,85
1488400

2
1,31
1364
1786,84
1,72
1860496

3
1,28
1417
1813,76
1,64
2007889

4
0,81
1548
1253,88
0,66
2396304

5
1,18
958
1130,44
1,39
917764

6
1,38
1233
1701,54
1,9
1520289

7
0,41
1365
559,65
0,17
1863225

8
0,92
848
780,16
0,85
719104

9
1,09
1333
1452,97
1,19
1776889

10
1,34
1475
1976,5
1,8
2175625

11
0,34
1698
577,32
0,12
2883204

12
1,84
1938
3565,92
3,39
3755844

13
1,35
1258
1698,3
1,82
1582564

14
1,25
1091
1363,75
1,56
1190281

15
1,02
1450
1479
1,04
2102500

16
1,41
1199
1690,59
1,99
1437601

17
1,08
1212
1308,96
1,17
1468944

18
0,43
295
126,85
0,18
87025

19
1,19
2182
2596,58
1,42
4761124

20
0,51
1277
651,27
0,26
1630729

21
1,27
1124
1427,48
1,61
1263376

22
1,15
1118
1285,7
1,32
1249924

23
0,70
562
393,4
0,49
315844

24
0,58
764
443,12
0,34
583696

25
1,43
1530
2187,9
2,04
2340900

26
0,74
679
502,46
0,55
461041

27
1,49
1108
1650,92
2,22
1227664

28
1,79
3132
5606,28
3,2
9809424

29
2,08
2306
4796,48
4,33
5317636

30
1,96
2301
4509,96
3,84
5294601

31
1,53
1347
2060,91
2,34
1814409

32
1,88
1835
3449,8
3,53
3367225

33
0,98
982
962,36
0,96
964324

34
1,68
2743
4608,24
2,82
7524049

35
1,65
2017
3328,05
2,72
4068289

36
1,78
2022
3599,16
3,17
4088484

37
0,93
723
672,39
0,86
522729

38
1,38
642
885,96
1,9
412164

39
1,56
1432
2233,92
2,43
2050624

40
1,17
699
817,83
1,37
488601

Итого
49,23
55 427
74 595,8
68,16
90790805


Связь предполагается линейная, уравнение прямой ух ср=а0+а1х

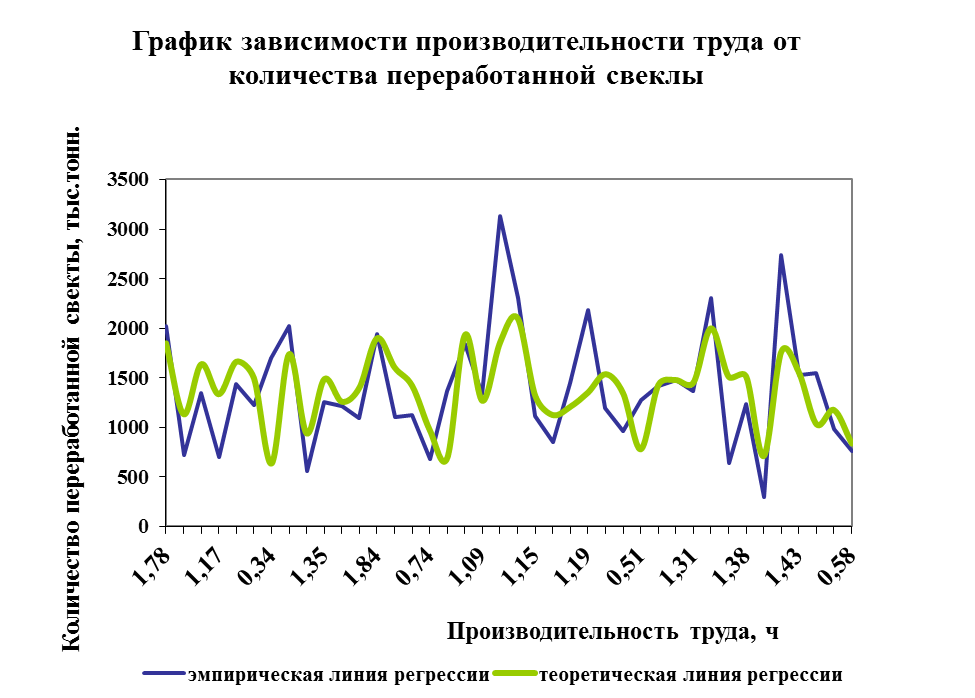
4 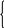0а + 49,23b= 55 427

49,23а + 68,16b = 74 595,8

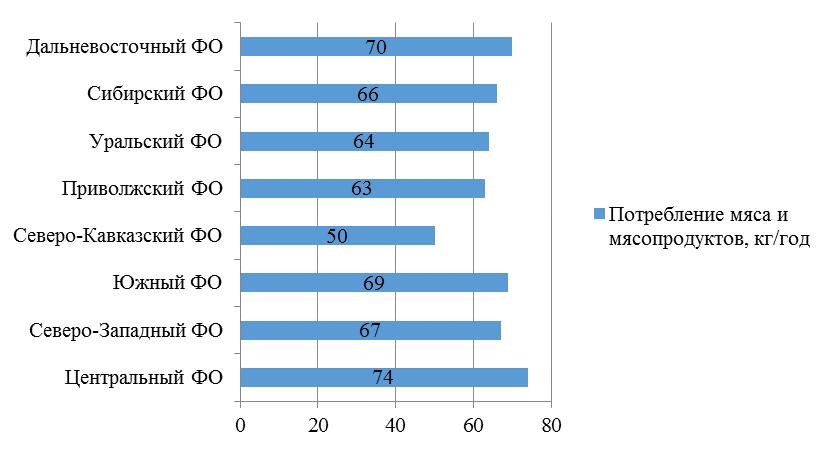
а 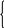= 349,2254

b = 842,1284
Таким образом, получим следующее уравнение ух ср = 349,2254 + 842,1284х

Коэффициент регрессии b свидетельствует о том, что при увеличении производительности труда на 1 пункт количество переработанной свеклы увеличится на 842,1284 тыс. т.

Тесноту связи определяем по линейному коэффициенту корреляции:
= 0,62

Следовательно, связь прямая и заметная.

Вычислим коэффициент детерминации:

r2 = 0,3844

Значит, доля вариации результативного признака у под влиянием вариации признака-фактора х составляет 0,3844.

Вычислим коэффициент эластичности:

842,13 = 0,75

Коэффициент эластичности показывает, что при увеличении производительности труда на 1 пункт переработка свеклы увеличится на 0,75 т.тонн.

Рассчитаем критерий значимости Стьюдента:

tрасч.= 0,62 * √38 / √(1-0,3844) = 4,87

tтабл.(0,05; 38) = 1,7167

Так как |tрасч.| > |tтабл.|, то вероятно, что найденное значение обусловлено только случайными колебаниями (то есть гипотеза о его случайности отклоняется).


Задание 2.2.


Результаты анализа проиллюстрируйте графиком зависимости.


Задание 3.1.

Сопоставьте по федеральным округам потребление мяса и мясопродуктов на душу населения в 2009 году с помощью полосовой диаграммы.



Задание 3.2.

Рассчитайте показатели динамики потребления мяса и мясопродуктов на душу населения в период с 2004 по 2009 гг. по Приволжскому федеральному округу, проанализируйте полученные результаты.
Показатели динамики потребления мяса и мясопродуктов на душу населения в период с 2009 по 2014 гг. по Приволжскому федеральному округу


Период
Потребление мяса и мясопродуктов, кг/год

2009
63,3

2010
64,1

2011
64,9

2012
66,1

2013
67,8

2014
69,4


Как мы видим с 2009 по 2014 год потребление мяса и мясопродуктов на душу населения по Приволжскому федеральному округу выросло на +6,1кг, то есть с 63,3 кг/год до 69,4 кг/год.

Задание 4.

По данным таблицы 2.1. постройте и рассчитайте индексы переменного состава, фиксированного состава и структурных сдвигов (для предприятий 1-5), покажите взаимосвязь и сделайте выводы.
Построение и расчет индексов переменного состава, фиксированного состава и структурных сдвигов

№
Количество выпущенной продукции, шт.
Затраты на выпуск продукции, тыс. чел./час.
Средние затраты на выпуск 1 ед. продукции, чел./час.
Затраты на выпуск продукции, при условии баз. Средние затраты на выпуск 1 ед. продукции, тыс. чел./час

базисный период, q0
отчетный период, q1
базисный период, p0q0
отчетный период, p1q1
p0
p0q1

1
1000
950
7830
7920
7,83
7 438,50

2
1100
1030
6520
6180
5,93
6 105,09

3
1200
1280
9143
9000
7,62
9 752,53

4
1300
1310
17800
18100
13,69
17 936,92

5
1400
1450
15100
15300
10,79
15 639,29

Итого
6000
6020
56 393
56 500
х
56 872,33


О пределим индекс переменного состава:

= : = 9,385 : 9,399 = 0,9985 или 99,85 %

Следовательно, в среднем по предприятиям средние затраты на выпуск 1 ед. продукции снизились на 0,15 %.

Определим индекс фиксированного состава:



= : = 9,385 : 9,447 = 0,9934 или 99,34%

За счет изменения затрат на выпуск продукции на каждом предприятии средние затраты на выпуск 1 ед. продукции снизились на 0,66%

Определим индекс структурных сдвигов:



= 9,447 : 9,399 = 1,0051 или 100,51%
За счет изменения количества выпущенной продукции на каждом предприятии, средние затраты на выпуск 1ед. продукции увеличились на 0,51 %.

С истема взаимосвязанных индексов при анализе динамики средних величин имеет вид:
= 0,9934 * 1,0051 = 0,9985.

Список источников





  1. Далингер В. А.,Симонженков С. Д., Галюкшов Б. С. Теория вероятностей и математическая статистика с применением mathcad. Учебник и практикум для СПО. М.: Юрайт, 2018. 146 с.

  2. Долгова В. Н., Медведева Т. Ю. Статистика. Учебник и практикум для СПО. М.: Юрайт, 2019. 246 с.

  3. Долгова В. Н., Медведева Т. Ю. Теория статистики. Учебник и практикум для академического бакалавриата. М.: Юрайт, 2019. 246 с.

  4. Дудин М. Н., Лясников Н. В., Лезина М. Л. Социально-экономическая статистика. Учебник и практикум. М.: Юрайт, 2019. 234 с.

  5. Ивашев-Мусатов О. С. Теория вероятностей и математическая статистика. Учебник и практикум для СПО. М.: Юрайт, 2017. 224 с.

Смотрите также файлы