По формуле (2.4) определяем среднее арифметическое значение :

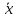(2.4)

где 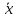- среднее арифметическое значение,

x_i – результаты замеров действительных размеров деталей,

N – величина выборки (число произведенных измерений).


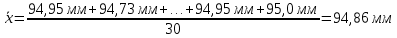
Среднее квадратичное отклонение S_x определяется по формуле (2.5):

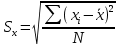(2.5)

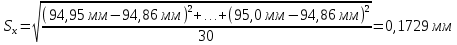
Среднее арифметическое значение характеризует положение кривой распределения на отсчетной шкале анализируемого параметра, а среднее квадратичное отклонение характеризует степень рассеяния случайной величины x относительно среднего арифметического значения.
2.2 Оценка точности технологической операции
Оценка точности технологических операций производится с использованием полученных выборочных статистических характеристик среднего арифметического значения 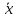и среднего квадратического отклонения 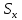путем определения показателей – коэффициента точности 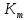, коэффициента настроенности 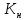, коэффициента смещения .

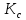Коэффициент точности определяется по формуле (2.6):

(2.6)

где ω – поле рассеяния размеров деталей.
Закон нормального распределения характеризуется полем рассеяния, которое определяет размах разброса значений случайной величины. Величину поля рассеяния  определяют по формуле (2.7):

---

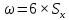	(2.7)

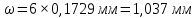
Точность технологического процесса оценивают исходя из следующих критериев:

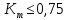– технологический процесс точный, удовлетворительный;

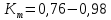– требует внимательного наблюдения;

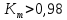– неудовлетворительный. В этом случае необходимо немедленно выяснить причину появления дефектных изделий и принять меры управляющего воздействия.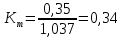



Таким образом, технологический процесс является точным.

Коэффициент настроенности определяется по формуле (2.8):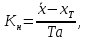

(2.8)

где 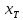– середина поля допуска, .

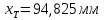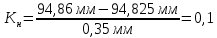
Так как значение коэффициента настроенности близко к нулю, можно сказать, что процент брака будет минимальным.

Коэффициент смещения определяется по формуле (2.9):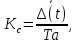

(2.9)

где 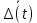– среднее значение отклонения контролируемого параметра относительно середины поля допуска в момент времени t.

Среднее значение отклонения контролируемого параметра относительно середины поля допуска в момент времени t определяется по формуле (2.10):

---

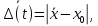(2.10)

где 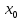– номинальный размер.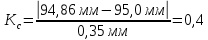

Таким образом, коэффициент точности показывает, что рассматриваемый процесс является точным, так как значение коэффициента меньше 0, 75. Процент брака будет минимальным, о чем говорит значение коэффициента настроенности, близкое к нулю ( 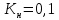). Коэффициент настроенности равен 0,4.
2.3 Оценка грубых погрешностей измерений и обработки
Грубые погрешности измерения и обработки нередко оказывают
решающее влияние на оценку точности технологических процессов и приводят к тому, что отдельные результаты наблюдений по своей величине значительно отличаются от других. Если технолог убеждён, что такие наблюдения – результат ошибки, то эти наблюдения не следует учитывать при анализе. Если же такой уверенности нет, то для определения того, являются ли резко выделяющиеся измерения результатом грубой ошибки или случайного отклонения, необходимо использовать один из методов обнаружения грубых погрешностей эксперимента (метод Грэббса, Ирвина, Романовского и др.).

Согласно методу Грэббса, предварительно по опытным данным выборки вычисляют характеристики распределения: среднее арифметическое значение 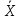и среднее квадратическое отклонение S. Затем определяют величину квантиля по формуле 2.11:

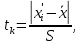(2.11)

где x_i' – резко выделяющееся (наибольшее или наименьшее) значение.

В расчете будет использоваться наибольшее значение из результатов замеров действительных размеров – 95,68 мм. Следовательно, квантиль равен:



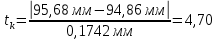
При технологических исследованиях чаще всего процент риска задают р=5% при котором грубая ошибка может быть принята за случайную. По таблице 2.1 в зависимости от объема выборки N находят критическое значение t

---

_к, которое сравнивают с ранее вычисленным значением t_к. Если t_к  t_к, то резко выделяющееся значение можно отбросить из опытных данных.

Таблица 2.1 – Допустимые критические значения t_к при р=5%

N	20	25	30	35	40	50	75	100
tк	2,620	2,717	2,792	2,839	2,904	2,956	3,102	3,187

Объем выборки значений равен 30, следовательно критическое значение t_к=2,792. Если сравнивать это значение с полученным выше значением квантиля t_к=4,70, то можно сделать вывод, что t_к < t_к, поэтому по методу Грэббса резко выделяющееся значение (95,68 мм) исключается и производится пересчет уточненных характеристик распределения и S_x.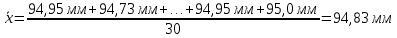





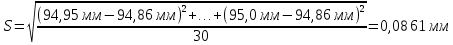
После исключения квантиль равен (в расчете будет использоваться наибольшее значение из результатов замеров действительных размеров – 95,0 мм.):



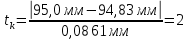
После исключения выделяющегося значения и пересчета основных характеристик было выяснено, что новое максимальное значение не является грубой ошибкой и не исключается из опытных данных.

Согласно методу Ирвина, для полученных экспериментальных данных определяют коэффициент по формуле 2.12:

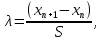(2.12)

где 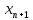, 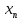– наибольшие значения из выборки,

– среднее квадратическое отклонение, вычисленное по всем значениям выборки.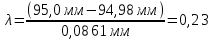

---

Этот коэффициент необходимо сравнить с табличным значением λ_q, некоторые возможные значения которого приведены в таблице 2.2.
Таблица 2.2 – Возможные значения коэффициента λ_q

Число измерений N	Уровень значимости q=0,05
1	2
3	2,2
10	1,5
30	1,2
100	1,0
1000	0,8

Если λ > λ_q , то нулевая гипотеза не подтверждается, то есть результат - ошибочный, и он должен быть исключен при дальнейшей обработке результатов наблюдений. При q=0,05 и числа измерений n=30 λ_q = 1,2. Так как 0,23<1,2, то максимальный результат не является ошибочным и по методу Ирвина не исключается из выборки.

Далее необходимо провести проверку близости эмпирического распределения к нормальному по критерию Романовского и по критерию Пирсона.

Согласно критерию согласия Пирсона, за меру расхождения эмпирического и теоретического распределений принимают величину :



где n_i – эмпирические частоты,

– теоретические частоты.
Применение критерия χ² к проверке гипотезы о нормальном распределении генеральной совокупности значений признака Х осуществляется по следующему правилу.

Необходимо вычислить теоретические частоты по формуле: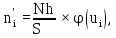


где N – объем выборки,

h – шаг.
Значение функции 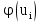находится табличным методом по приложению 1 учебного пособия В. И. Губина. Данные для вычисления теоретических частот

---

Смотрите также файлы

• Теоретические основы управления персоналом в условиях кризиса 4.docx

• Сценарий классного часа До свидания, 1 класс!.docx

• Алгоритмдеу жне программалау Педагогты атыжні.docx

• Кгэу министерство науки и высшего образования российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования.docx

• язык и речь.docx