ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 207
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1. Исследование процессов фильтрации сигналов.
Задание 1. Исследование амплитудного фильтра
Задание 2. Исследование полосового амплитудного фильтра.
Задание 3. Исследование амплитудного детектора.
Часть 2 Точечные оценки исследуемого процесса
Задание 4. Формирование оценки выборки сигнала
Excel, обеспечивающее амплитудную селекцию значений сигнала.
Указание.
Задание 3.2
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль выделения значений сигнала на приемнике, а диапазоне
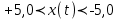
Указание.
В среде Microsoft Excel зададим условия задания, где =1, t=0.17, t0=0.1, a=0.5, i = 1….52.
Формула x(t) в программной среде MS Excel будет так: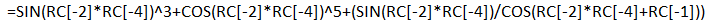
Итоговый модуль подсчета амплитудных значений будет выглядеть следующим образом:
Зададим условия сигнала вывода амплитудных значений сигнала x(t) ∈ (-2;2) и x(t) ∈ (-5;5).
К заданию 3.1. x(t) ∈ (-2;2):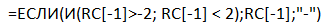 ;
;
К заданию 3.2. x(t) ∈ (-5;5):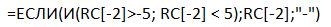 , где формула «если» определяет соответствие столбца x(t) заданному условию и если значение соответствует, то выводит его, иначе выводит прочерк в заданной ячейке.
, где формула «если» определяет соответствие столбца x(t) заданному условию и если значение соответствует, то выводит его, иначе выводит прочерк в заданной ячейке.
Вид полного модуля обработки данных сигнала:
По условию задания требуется выделить максимальные значения сигнала, поступающие на приемник. Для выделения искомых значений воспользуемся функцией МАКС().
Результат:
График 3.1.
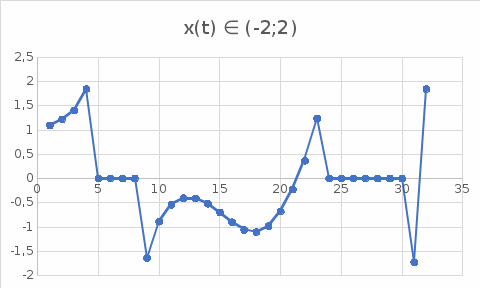
График 3.2.
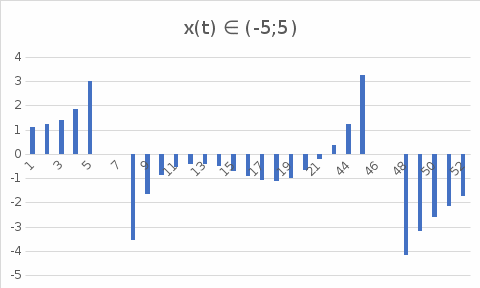
Поиск максимальных и минимальных значений сигнала в диапазоне удобнее всего осуществлять с помощью функций МИН(), МАКС().
В десяти независимых измерениях температуры процессора, установленного на компьютере, получены следующие значения:
Таблица 4.1
Задание 4.1
Вычислить значение выборочной дисперсии по данному распределению выборки (таблица 4.1).
Вычислить значение выборочной дисперсии по данному распределению выборки по следующим данным - таблица 4.2.
Таблица 4.2
Задание 4.2
Вычислить значение исправленной выборочной дисперсии по данному распределению выборки: таблица 4.1 и таблица 4.2.
Задание 4.1
В программной среде MS Excel вычислим значения выборочной дисперсии по данному распределению выборки для таблиц 4.1. и 4.2.
Условие задания в MS Excel будет выглядеть так:
Таблица 4.1.
Таблица 4.2.
Найдем для обеих таблиц несмещенную оценку генеральной средней, определяемую по выражению:

1.
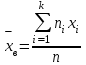
где xi варианта выборки; ni частота встречаемости варианты xi в выборке, и количество значений (вариант) в выборке определяется выражением:

2.
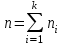
Формула для среды MS Excel будет выглядеть так: =(A4*B4+A5*B5+A6*B6)/C4
Для таблицы 4.1. значение хв=45.41, для таблицы 4.2. значение хв=28.93.
Далее найдем Смещенной оценкой генеральной дисперсии служит выборочная средняя, определяемая по выражению:

3.
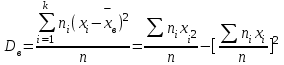
Проведем для подсчета значений выборочной дисперсии по данному распределению выборки промежуточные расчеты и получим итоговые цифры в графе Dв.
Указание.
-
При создании фильтра – детектора , использовать логическую процедуру «ЕСЛИ ………., ТОГДА ……….» в среде Excel -
Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
Задание 3.2
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль выделения значений сигнала на приемнике, а диапазоне
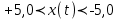
Указание.
-
При создании фильтра - детектора, использовать логическую процедуру «ЕСЛИ ………., ТОГДА ……….» в среде Excel -
Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel. -
Проиллюстрировать полученные результаты. Сопоставить результаты исполнения заданий 3.1 и 3.2, сделать выводы
Выполнение задания 3.
В среде Microsoft Excel зададим условия задания, где =1, t=0.17, t0=0.1, a=0.5, i = 1….52.
| i | t | dt | ω | a |
| 1 | 0,1 | 0,17 | 1 | 0,5 |
| 2 | 0,27 | 0,17 | 1 | 0,5 |
| 3 | 0,44 | 0,17 | 1 | 0,5 |
| 4 | 0,61 | 0,17 | 1 | 0,5 |
| 5 | 0,78 | 0,17 | 1 | 0,5 |
| 6 | 0,95 | 0,17 | 1 | 0,5 |
Формула x(t) в программной среде MS Excel будет так:
Итоговый модуль подсчета амплитудных значений будет выглядеть следующим образом:
| i | t | dt | ω | a | x(t) |
| 1 | 0,1 | 0,17 | 1 | 0,5 | 1,097225 |
| 2 | 0,27 | 0,17 | 1 | 0,5 | 1,222028 |
| 3 | 0,44 | 0,17 | 1 | 0,5 | 1,40571 |
| 4 | 0,61 | 0,17 | 1 | 0,5 | 1,846269 |
| 5 | 0,78 | 0,17 | 1 | 0,5 | 2,982315 |
| 6 | 0,95 | 0,17 | 1 | 0,5 | 7,354967 |
| 7 | 1,12 | 0,17 | 1 | 0,5 | -17,5558 |
Зададим условия сигнала вывода амплитудных значений сигнала x(t) ∈ (-2;2) и x(t) ∈ (-5;5).
К заданию 3.1. x(t) ∈ (-2;2):
К заданию 3.2. x(t) ∈ (-5;5):
Вид полного модуля обработки данных сигнала:
| i | t | dt | ω | a | x(t) | x(t) ∈ (-2;2) | x(t) ∈ (-5;5) |
| 1 | 0,1 | 0,17 | 1 | 0,5 | 1,097225 | 1,097225171 | 1,097225171 |
| 2 | 0,27 | 0,17 | 1 | 0,5 | 1,222028 | 1,222028249 | 1,222028249 |
| 3 | 0,44 | 0,17 | 1 | 0,5 | 1,40571 | 1,405709887 | 1,405709887 |
| 4 | 0,61 | 0,17 | 1 | 0,5 | 1,846269 | 1,846269381 | 1,846269381 |
| 5 | 0,78 | 0,17 | 1 | 0,5 | 2,982315 | - | 2,982314957 |
| 6 | 0,95 | 0,17 | 1 | 0,5 | 7,354967 | - | - |
| 7 | 1,12 | 0,17 | 1 | 0,5 | -17,5558 | - | - |
| 8 | 1,29 | 0,17 | 1 | 0,5 | -3,52992 | - | -3,529917923 |
| 9 | 1,46 | 0,17 | 1 | 0,5 | -1,63749 | -1,637487699 | -1,637487699 |
По условию задания требуется выделить максимальные значения сигнала, поступающие на приемник. Для выделения искомых значений воспользуемся функцией МАКС().
Результат:
| 50 | 4,86 | 0,17 | 1 | 0,5 | -2,60723 | - | -2,607231776 | ||
| 51 | 5,03 | 0,17 | 1 | 0,5 | -2,15658 | - | -2,156576915 | ||
| 52 | 5,2 | 0,17 | 1 | 0,5 | -1,72535 | -1,725348119 | -1,725348119 | ||
| Максимальные значения x(t) в диапазоне | 1,846269381 | 3,240065197 | |||||||
Графики к заданию 3.
График 3.1.

График 3.2.
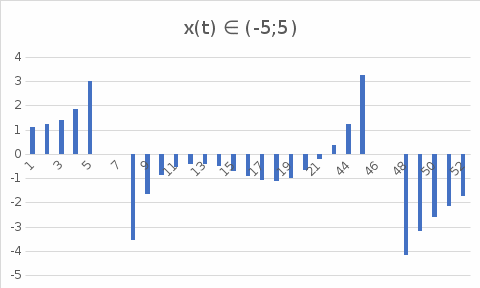
Вывод по заданию 3.
Поиск максимальных и минимальных значений сигнала в диапазоне удобнее всего осуществлять с помощью функций МИН(), МАКС().
Часть 2 Точечные оценки исследуемого процесса
Задание 4. Формирование оценки выборки сигнала
В десяти независимых измерениях температуры процессора, установленного на компьютере, получены следующие значения:
Таблица 4.1
| Температурные значения процессора Тi | 38.6 | 48.2 | 45.3 |
| ni | 2 | 5 | 3 |
| n | 10 | ||
Задание 4.1
Вычислить значение выборочной дисперсии по данному распределению выборки (таблица 4.1).
Вычислить значение выборочной дисперсии по данному распределению выборки по следующим данным - таблица 4.2.
Таблица 4.2
| Температурные значения процессора Тi | 31,1 | 28,6 | 27,2 |
| ni | 3 | 4 | 3 |
| n | 10 | ||
Задание 4.2
Вычислить значение исправленной выборочной дисперсии по данному распределению выборки: таблица 4.1 и таблица 4.2.
Выполнение задания 4.
Задание 4.1
В программной среде MS Excel вычислим значения выборочной дисперсии по данному распределению выборки для таблиц 4.1. и 4.2.
Условие задания в MS Excel будет выглядеть так:
Таблица 4.1.
| варианта выборки | частота встречаемости xi | количество значений в выборке |
| xi | ni | n |
| 38,6 | 2 | 10 |
| 48,2 | 5 | 10 |
| 45,3 | 3 | 10 |
Таблица 4.2.
| варианта выборки | частота встречаемости xi | количество значений в выборке |
| xi | ni | n |
| 31,1 | 3 | 10 |
| 28,6 | 4 | 10 |
| 27,2 | 3 | 10 |
Найдем для обеих таблиц несмещенную оценку генеральной средней, определяемую по выражению:

1.
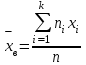
где xi варианта выборки; ni частота встречаемости варианты xi в выборке, и количество значений (вариант) в выборке определяется выражением:

2.
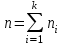
Формула для среды MS Excel будет выглядеть так: =(A4*B4+A5*B5+A6*B6)/C4
Для таблицы 4.1. значение хв=45.41, для таблицы 4.2. значение хв=28.93.
Далее найдем Смещенной оценкой генеральной дисперсии служит выборочная средняя, определяемая по выражению:

3.
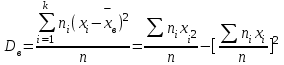
Проведем для подсчета значений выборочной дисперсии по данному распределению выборки промежуточные расчеты и получим итоговые цифры в графе Dв.
| Для таблицы 4.1. | Для таблицы 4.2. | ||
| Σ ni*xi | 454,1 | Σ ni*xi | 289,3 |
| Σ ni*xi^2 | 20752,39 | Σ ni*xi^2 | 8392,99 |
| хв | 45,41 | хв | 28,93 |
| Dв | 13,1709 | Dв | 2,3541 |