Файл: Исследование процессов фильтрации сигналов.docx

При этом формулы будут иметь вид:

Σ ni*xi = =A4*B4+A5*B5+A6*B6;

Σ ni*xi^2 = =A4^2*B4+A5^2*B5+A6^2*B6;

D_в =(I3/C4)-(I2/C4)^2.

Задание 4.2

Вычислим значение исправленной выборочной дисперсии по данному распределению выборки для таблиц 4.1 4.2. по формуле:

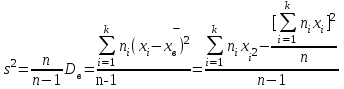4

Таблица 4.1.		Таблица 4.2.
Σ ni*xi	454,1	Σ ni*xi	289,3
Σ ni*xi^2	20752,39	Σ ni*xi^2	8392,99
хв	45,41	хв	28,93
Dв	13,1709	Dв	2,3541
s^2	14,63433333	s^2	2,615666667

Где формула s^2 будет иметь вид:

s^2 =(I3-(I2^2/C4))/(C4-1).

---

Вывод по заданию 4.

В программной среде MS Excel удобно считать дисперсию и математическое ожидание. Можно сделать промежуточный вывод: чем меньше значения в выборке и частота встречаемости ближе к средним значениям, тем меньше будет дисперсия и математическое ожидание.

Задание 5. Формирование оценки коррелированности сигналов

На приемник поступают два сообщения – два сигнала, описываемые выражениями (5.1) и (5.2). Требуется установить степень тождественности – схожести сигналов. С этой целью проводится вычисление корреляционной функции.

Задание 5.1

Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:

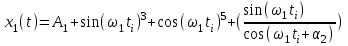5.1.1

При условии: А₁= 0 ; ₁ = 480 ; i= 1,2,3,……. ,52; ₁ = 0

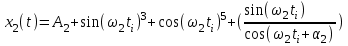5.1.2

При условии: А₂= 50 ; ₂ = 240,260,280, ……520 ; i= 1,2,3,……. ,52; ₂ = 0
Задание 5.2

Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:

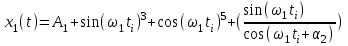5.2.1

При условии: А₁= 0 ; ₁ = 480 ; i= 1,2,3,……. ,52; ₁ = 0

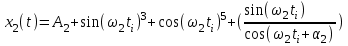5.2.2

При условии: А₂= 50 ; ₂ =480; i= 1,2,3,……. ,52; ₂ = 0,25;0.5;0.75;……;4.0

Выполнение задания 5.

Задание 5.1

Зададим условия задачи в программном комплексе MS Excel:

n = 52		ДАНО						уравнение 1		уравнение 2
i	ti	A1	А2	ω1	ω2	a1	a2		x1		x2
1	1	0	50	480	240	0	0		-0,851564138		53,75085684
2	2	0	50	480	260	0	0		-4,939554198		33,9720948
3	3	0	50	480	280	0	0		3,010221716		51,72141683
4	4	0	50	480	300	0	0		-0,112228301		50,89131837
5	5	0	50	480	320	0	0		0,740368682		50,74796643
6	6	0	50	480	340	0	0		-0,835392049		51,26336968
7	7	0	50	480	360	0	0		-15,97330416		51,155082
8	8	0	50	480	380	0	0		2,092880607		47,57024386
9	9	0	50	480	400	0	0		-0,491180874		50,54744523
10	10	0	50	480	420	0	0		0,316077786		48,92447084
11	11	0	50	480	440	0	0		-1,042721364		48,26829602
12	12	0	50	480	460	0	0		8,061457451		49,33131723
13	13	0	50	480	480	0	0		1,556084037		51,55608404
14	14	0	50	480	500	0	0		-0,824653561		51,19422018
15	15	0	50	480	520	0	0		-0,238191451		49,09629478

---

Поскольку t жестко не задано, будем измерять его с интервалом 1 секунду в течение 52 секунд (в готовом модуле можно задать любое значение t), а уравнения 1 и 2 зададим выражениями:

1. 
   =(C3+SIN(E3*B3))^3+(COS(E3*B3))^5+(SIN(E3*B3)/COS(E3*B3+G3));
   
2. 
   =D3+(SIN(F3*B3)^3+COS(F3*B3)^5+(SIN(F3*B3)/(COS(F3*B3)+H3))).
   

Для вычисления коэффициента корреляции, по условию задания, нам потребуется провести несколько промежуточных расчетов.

Вычисление x1 и x2 среднего проведем по формуле:



Формула будет иметь вид: =СРЗНАЧ(I3:I54).

x1 ср	x2 ср
-0,03750373	50,01657294
-0,03750373	50,01657294
-0,03750373	50,01657294
-0,03750373	50,01657294
-0,03750373	50,01657294

Д 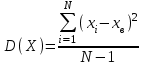алее подсчитаем столбец x_i-x_в для каждого уравнения и выведем в итогах столбца сумму по столбцу. Это необходимо для вычисления значения дисперсии, определяемой по формуле:

x1- x1 ср	x1-x1 ср^2
-0,81406	0,66269434
-4,90205	24,03009875
3,047725	9,288630422
-0,07472	0,005583761
0,777872	0,605085496
-0,79789	0,636625762
-15,9358	253,9497352
2,130384	4,538537442
-0,45368	0,205822947
0,353582	0,125019892
-1,00522	1,010462483

---

Посчитаем дисперсию для каждого уравнения:

D(x1)	90,12293
D(x2)	92,36894

Формула будет иметь вид: =Q55/(A54).

Далее посчитаем корреляционный момент (коэффициент ковариации) по формуле:



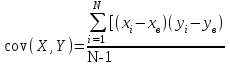
Для вычислений коэффициента введем еще 3 столбца с промежуточными расчетами и итоговой суммой под столбцом.

x1- x1 ср	x2 - x2 ср	(x1-x1 ср)*(x2 - x2 ср)
-0,8140604	3,73428391	-3,039932663
-4,9020505	-16,044478	78,6508415
3,0477255	1,7048439	5,195896132
-0,0747246	0,87474543	-0,065364973
0,7778724	0,7313935	0,568930826
-0,7978883	1,24679674	-0,994804548
-15,9358	1,13850907	-18,14305327
2,1303843	-2,4463291	-5,211621155
		………………………..
		761,0502824
		Σ (x1-x1 ср)*(x2 - x2 ср)

Теперь можем вычислить коэффициент ковариации по формуле: =T55/A54

Проведем вычисления коэффициента корреляции по выражению:

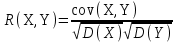D(x1)	90,12293
D(x2)	92,36894
cov(x1,x2)	14,63558
R (x1,x2)	0,160409

---

Где формула R(x1, x2) будет иметь вид: =B62/(КОРЕНЬ(B60)*КОРЕНЬ(B61))

Проведем проверку вычисленного значения встроенной функцией КОРЕЛЛ.

КОРРЕЛ

0,16

Где, формула для вычислений для столбцов x1 и x2 будет иметь вид: =КОРРЕЛ(J3:J54;I3:I54).

Вычисленные значения совпадают.

Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения rxy < 0.3 свидетельствуют о слабой связи, значения rxy от 0.3 до 0.7 - о связи средней тесноты, значения rxy > 0.7 - о сильной связи.

Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:

Абсолютное значение rxy	Теснота (сила) корреляционной связи
менее 0.3	слабая
от 0.3 до 0.5	умеренная
от 0.5 до 0.7	заметная
от 0.7 до 0.9	высокая
более 0.9	весьма высокая

Полученное значение коэффициента корреляции <0.3, следовательно, между выражениями слабая корреляционная связь.

Найдем значение t-критерия для оценки статистической значимости корреляционной связи по формуле:



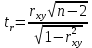
Полученное значение t_r сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает t_крит, то делается вывод о статистической значимости выявленной корреляционной связи.

Tr	1,149145378
Критическое значение tкрит найдем по таблице критических значений корреляции Пирсона
к=n-2	50	число степеней свободы
р	0,01	уровень значимости
tкрит	0,451	по таблице корреляции Пирсона
ИТОГ	Статистически значимо	если Тр больше Ткрит то связь является статистически значимой

---