Файл: Учебное пособие в двух частях Часть Основы теории.doc

Она подчиняется экспоненциальному закону распределения времени безотказной работы изделия и одинакова в любых одинаковых промежутках времени в период нормальной эксплуатации.

Экспоненциальное распределение описывает:

1) наработку до отказа объектов, у которых в результате сдаточных испытаний (выходного контроля) отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации. Примеры таких объектов: сложные технические системы с множеством компонентов, средства вычислительной техники, системы автоматического регулирования и т. п.;

2) схему возникновения внезапных, мгновенных повреждений устройств. В этом случае отказ не зависит от состояния самого устройства, а является следствием внешних усло­вий его эксплуатации (ударных нагрузок, температурных условий и т. п.).

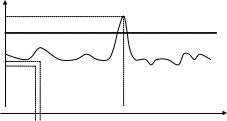
Внешняя нагрузка является случайной из-за неизбежных случайных колебаний внешних условий и неизбежных случайных отклонений взаимодействия элементов в системе. Нагрузка изменяется непрерывно и относительно плавно (рис. 4.2).
S (t)

S₃

S_пред

S₂

S₁


t₁t₂ t₃t

Рис. 4.2. Процесс изменения некоторой нагрузки
Это означает, что если взять два соседних момента времени t₁ и t₂, то соответствующие им нагрузки S₁и S₂ будут связаны друг с другом. Так, еслиS₁ мала, то маловероятно, что S₂будет велика. Это утверждение тем более верно, чем меньше интервал Sвремениt₁ – t₂. В то же время, если взять участки времени, значительно удаленные друг от друга(t₂ и t₃), то величинаS₃ будет мало зависеть от величиныS₂.

Описанное свойство нагрузки называется асимптотической независимостью нагрузкиS₃ отS₂, когда разностьt₃– t₂ велика. Асимптотическая независимость отражает тот факт, что связь междуS₃иS₂существует и уменьшается по мере роста разности t₃– t₂ .

Пиковые значения нагрузки при её плавном изменении возникают также случайно, в силу чего невозможно предсказать момент их появления. При этом отсутствие направленного изменения нагрузки называется ее стационарностью.

---

Любой элемент имеет ограниченную прочность. Поэтому имеется некоторая предельная нагрузка S_пред,которую система способна выдержать без отказа. Если некоторое текущее значение нагрузки S_i превзойдет S_пред, то в соответствующий этому событию момент времени t_i произойдет внезапный отказ.
При этом уровень предельной нагрузки S_пред остается, как правило, постоянным в течение всего времени эксплуатации элемента.

Таким образом, внезапный отказ наступает не как следствие постепенного изменения внутреннего состояния элемента, а лишь как результат внешнего случайного воздействия, имеющего величину больше допустимого. В силу этого внезапный отказ наблюдается чаще всего в начальный момент времени эксплуатации устройства. Становится очевидным, что при внезапных отказах нет смысла прибегать к профилактическим мерам типа предварительной замены элементов или их периодического ремонта.

Единственный путь повышения надёжности при внезапных отказах –конструктивное улучшение элементов или уменьшение величин действующих нагрузок.

Экспоненциальное распределение широко применяется для оценки надёжности в период нормальной эксплуатации.

Плотность распределения времени безотказной работы находится по следующей формуле:

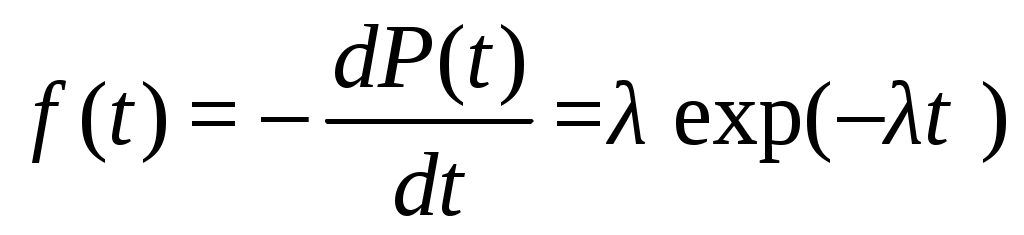. (4.4)

Графики изменения показателей безотказной работы при экспоненциальном распределении приведены на рис. 4.3.

Числовые характеристики наработки до отказа:

– средняя наработка до отказа

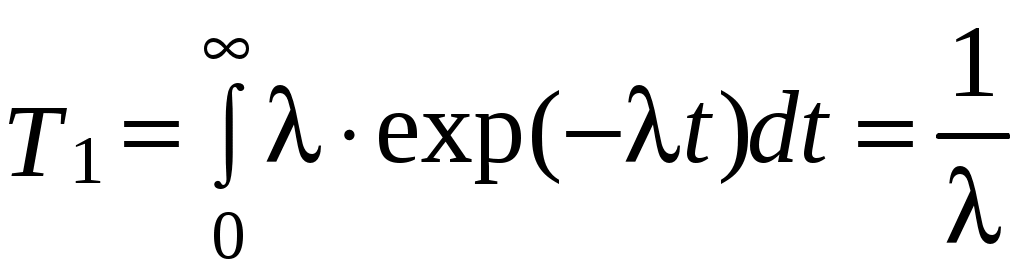; (4.5)

– дисперсия наработки до отказа

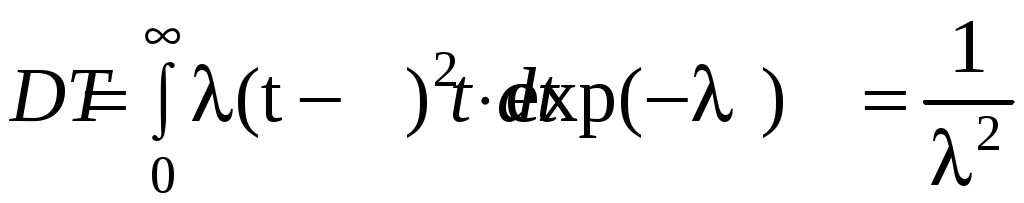. (4.6)

f(t) P(t)

1


1/T₀



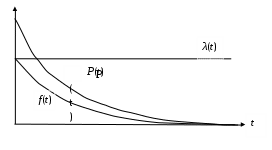
Рис. 4.3. Графики функций показателей безотказности
при экспоненциальном распределении
При t << 1, т. е. при наработке t много меньшей, чем средняя наработ- ка T, выражение (4.3) можно упростить, заменив двумя первыми членами разложения в степенной ряд.

Например, выражение для вероятности безотказной работы (ВБР) примет вид:

---

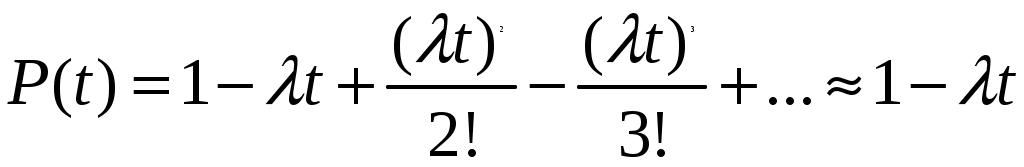, (4.7)

при этом погрешность вычисленияP(t) не превышает (λt)²/2.

Для упрощенного вычисления вероятности безотказной работы можно использовать табл. 4.1.
Таблица 4.1

Упрощенное вычисление вероятности безотказной работы

	1,0	0,1	0,01	0,001	0,0001
P(t)	0,368	0,9	0,99	0,999	0,9999

Так, при вероятность P(t)= 0,37, т. е. 63 % отказов возникает за время t < T, а 37 % – позднее. Из приведённых значений следует, что для обеспечения высокой вероятности безотказной работы, например 0,9 или 0,99, можно использовать только малую долю среднего срока службы – 0,1 и 0,01 соответственно.

Если работа изделия происходит при разных режимах и разных интенсивностях отказов λ_i, то при этом верно условие:

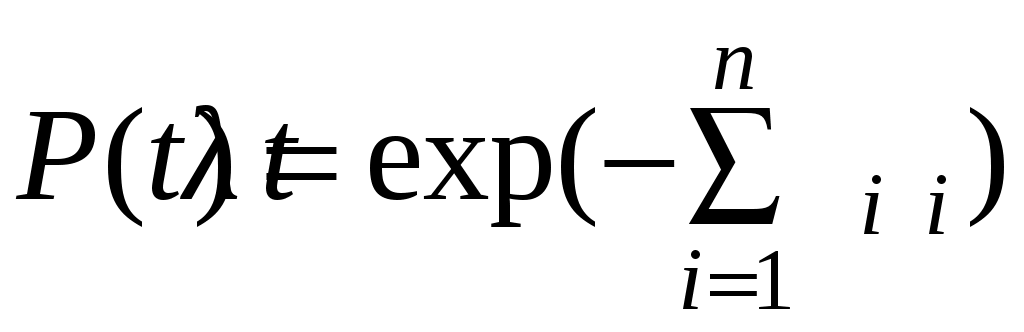, (4.8)

где t_i – продолжительность работы в i-м режиме.
Контрольные вопросы и задачи

1. Чем вызваны отказы в период нормальной эксплуатации?

2. Как описывается изменение плотности распределения отказов при экспоненциальном распределении наработки до отказа?

3. Известно, что серийно выпускаемая деталь имеет экспоненциальное распределение наработки до отказа с параметром λ = 10^–5 ч^–1. Деталь используется конструктором при разработке нового прибора. Назначенный ресурс прибора предполагается T_н = 10⁴ ч. Определить: а) среднюю полезную наработку детали к моменту T_н; б) вероятность того, что деталь безотказно проработает в интервале наработки [0, T_н].

Ответы: 1) 9,5 · 10³ ч, 2)0,905.

4.3. Надёжность объектов при постепенных отказах

---

Постепенным отказам свойственны законы распределения времени безотказной работы, дающие сначала низкую плотность распределения, затем рост плотности и затем падение, связанное с уменьшением числа работоспособных объектов.

Многообразие причин и условий возникновения отказов в этот период приводит к необходимости применения нескольких законов распределений, которые устанавливаются путем аппроксимации результатов испытаний или наблюдений в эксплуатации.

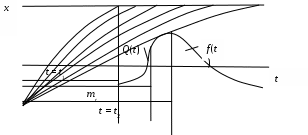
Пример формирования распределения f(t) показан на графике изменения выходного параметра ряда механизмов, например потери точности металлорежущих станков одной марки в процессе эксплуатации (рис. 4.4).

t

Рис. 4.4. Формирование закона распределения времени
безотказной работы f(t)

На этом рисунке показано:

t₁ – время работы, при котором появляются первые признаки от­казов;

t₂ – время работы, при котором исчерпываются потенциальные возможности безотказной работы;

m_t– математическое ожидание срока службы;

t – время работы в интервале t₂ – t₁, определяющее вероятность безотказной работы P(t);

Q(t) = 1 – P(t) – вероятность отказов во время работы в интервале t₂ – t₁.

---

4.3.1. Нормальный закон распределения наработки до отказа

Нормальное распределение вероятности безотказной работы описывает схему длительного «естественного» старения (постепенные отказы). В этом случае отказы являются следствием накопления повреждений:

– при постоянной скорости износа;

– однородном начальном качестве объектов.

При таких начальных условиях большая часть отказов наблюдается в течение конечного периода работы объекта.

Нормальное распределение, или распределение Гаусса, является наиболее универсальным, удобным и широко применимым.

Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы.

Нормальному распределению подчиняются наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры, ошибки измерения деталей и т. д.

Плотность распределения отказов описывается формулой

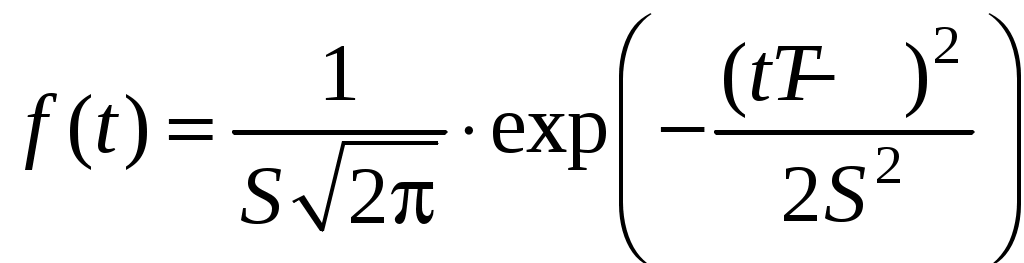. (4.9)

Распределение имеет два независимых параметра: математическое ожидание m_t и среднее квадратическое отклонение S.

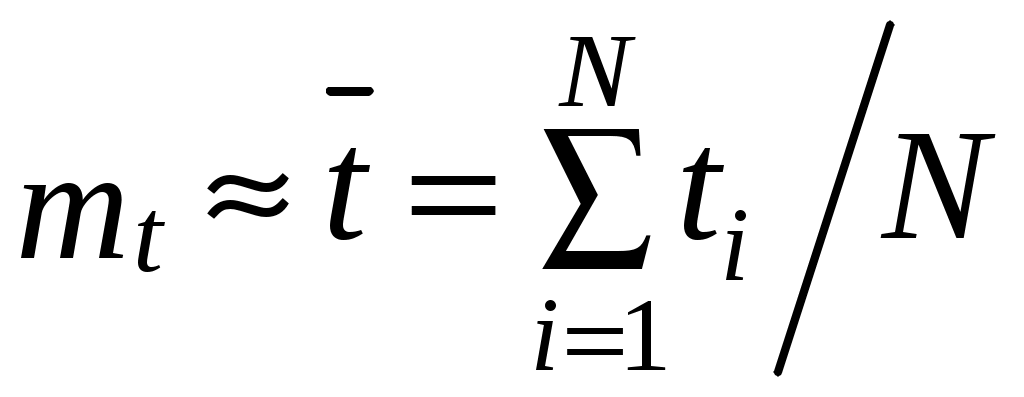, (4.10)

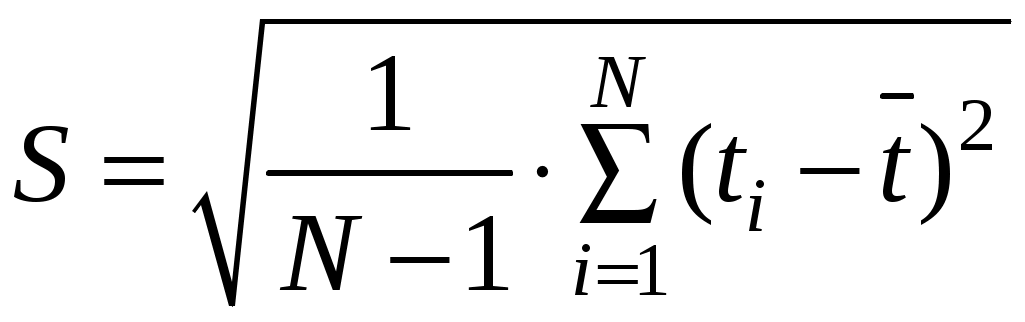. (4.11)

Графики изменения показателей безотказности при нормальном распределении приведены на рис. 4.5.

Выясним смысл параметров Ти S нормального распределения. Из графика f(t) видно, что Т является центром симметрии распределения, поскольку при изменении знака разности (t – Т) выражение (4.9) не меняется. При t = Т функция f(t) достигает своего максимума:

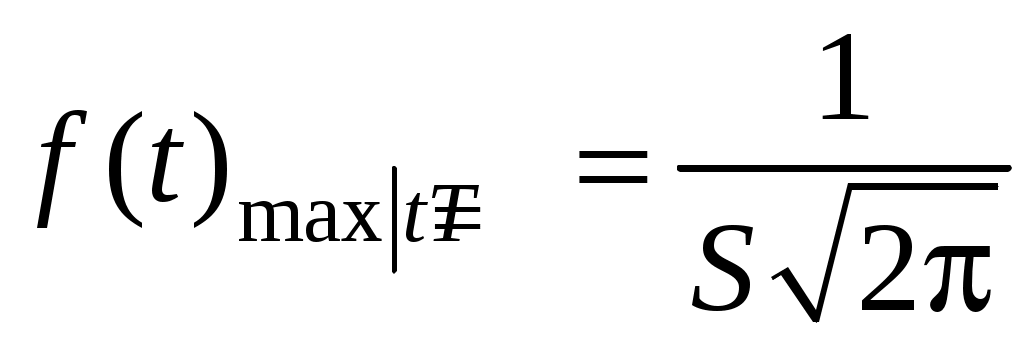. (4.12)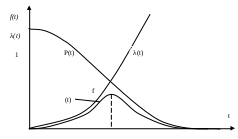



Рис. 4.5. Графики функций показателей безотказности при нормальном распределении

Параметр S характеризует форму кривой f(t), т. е. рассеивание случайной величины T. Кривая плотности распределения f(t) тем выше и острее, чем меньше S. Она начинается от t = –∞ и распространяется до

---