Файл: Учебное пособие в двух частях Часть Основы теории.doc

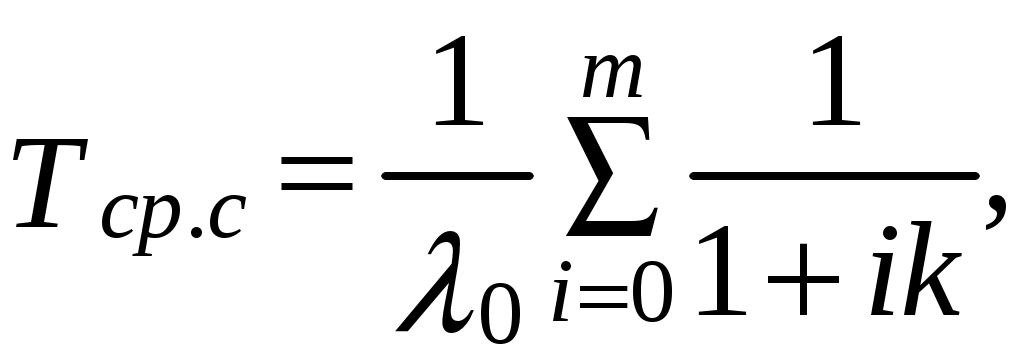(6.12)

_где 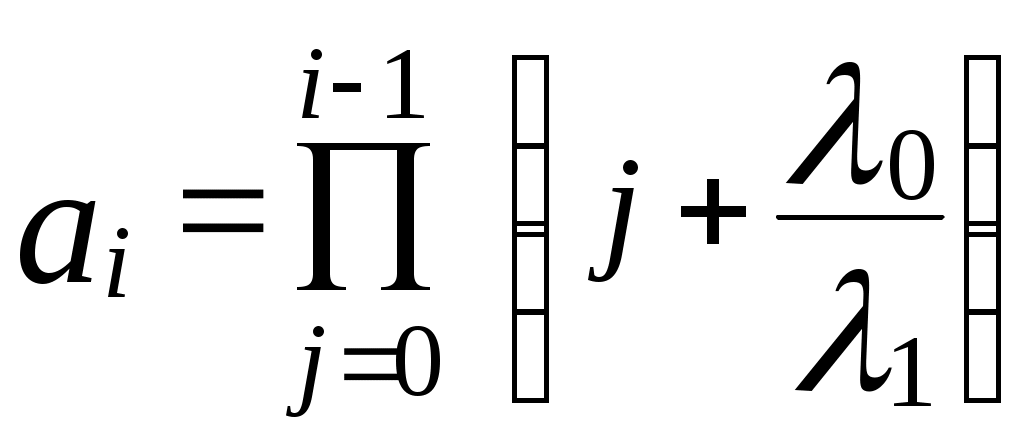; ; 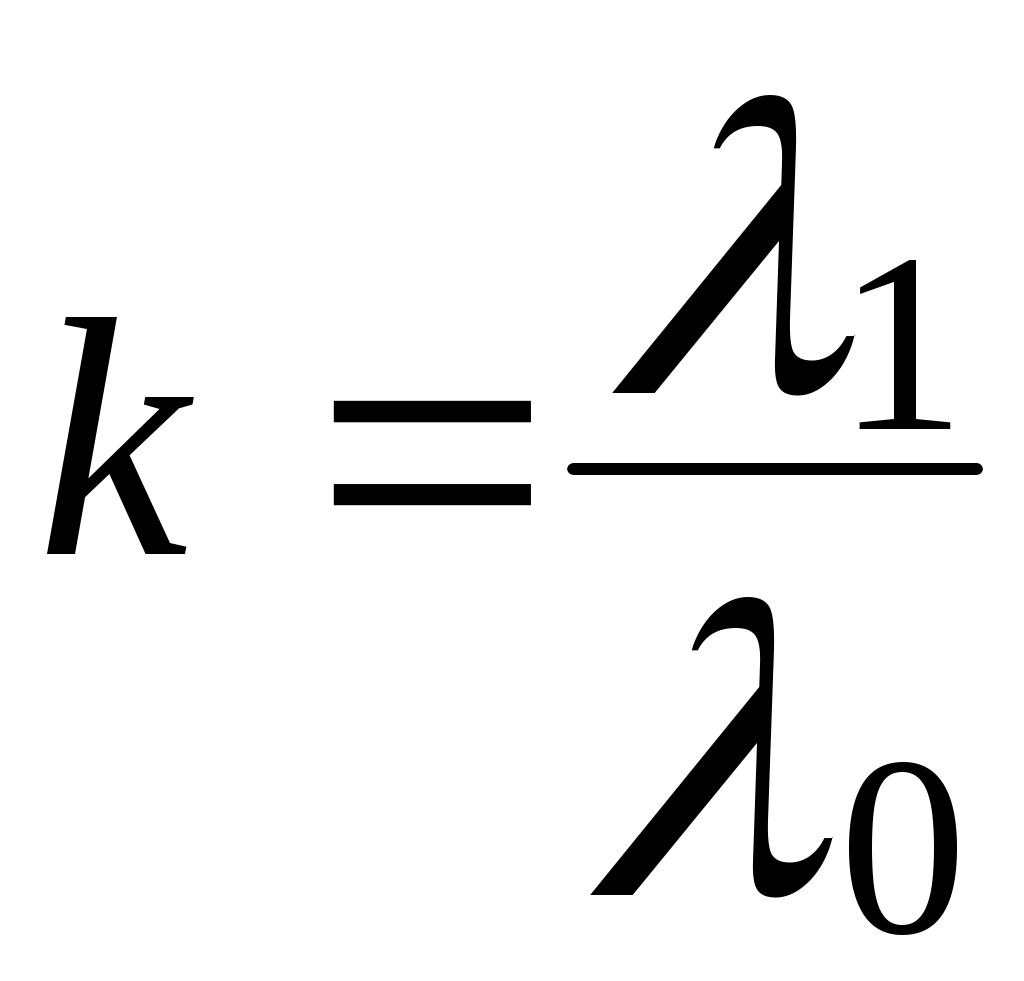λ₁ – интенсивность отказов резервного устройства до замещения.

При нагруженном состоянии резерва формулы для Р_с(t)и Т_ср.ссовпадают с (6.2).

4. Раздельное резервирование замещением с целой кратностью (рис. 6.1, г):

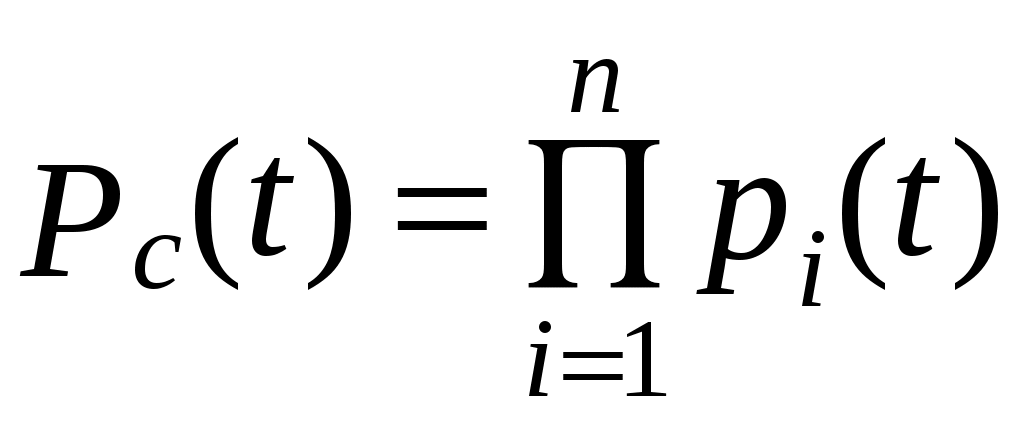, (6.13)

где p_i(t) – вероятность безотказной работы системы из-за отказов элементов i-го типа, резервированных по способу замещения. Вычисляетсяp_i(t)по формулам общего резервирования замещением (формулы (6.8), (6.9), (6.11)).

5. Общее резервирование с дробной кратностью и по­стоянно включенным резервом (рис. 6.1, д):

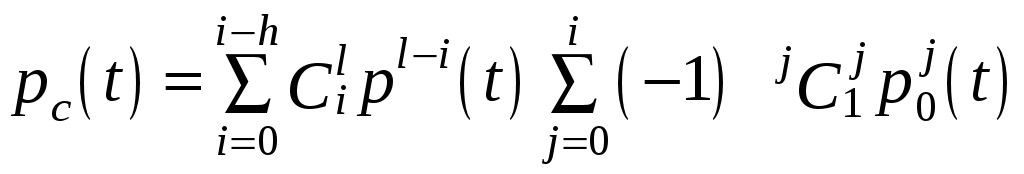, (6.14)

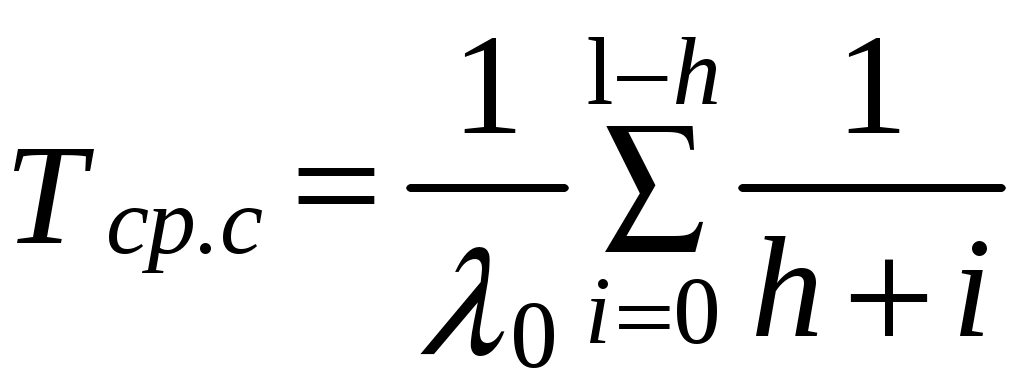, (6.15)

где p₀(t)– вероятность безотказной работы основного или любого резервного элемента;

l– общее число основных и резервных систем;

h– число систем, необходимых для нормальной работы резервированной системы.

В данном случае кратность резервирования

m = (l– h)/h. (6.16)

6. Скользящее резервирование:





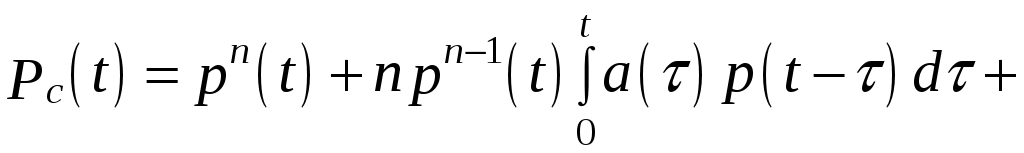
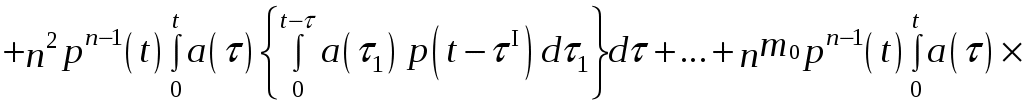
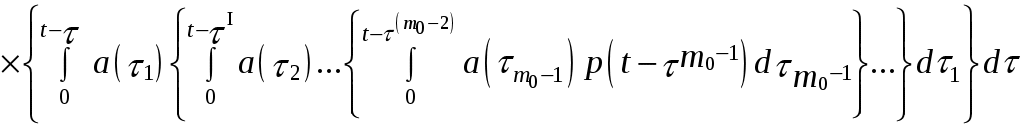
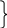_{dτ, (6.17)}

где τ^I= τ + τ₁; τ^II= τ + τ₁+ τ₂…; = τ + τ₁+…+ ; n – число элементов основной системы; m₀– чис­ло резервных элементов; p(t–t_i) – вероятность безотказ­ной работы одного элемента в течение времени (

---

t–t_i);

, , ;a(τ_i)– частота отказов одного из основных элементов в момент времени τ_i, τ₁, … .

При экспоненциальном законе надежности



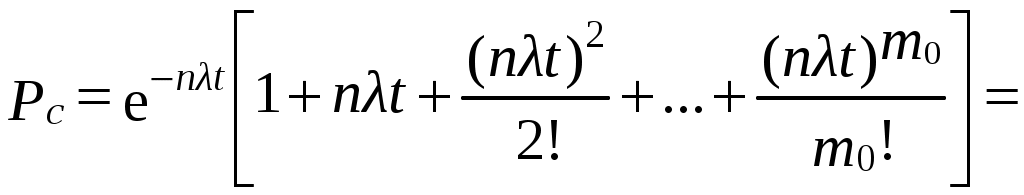
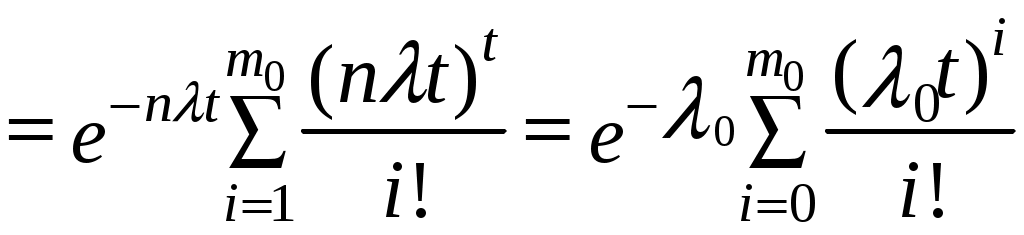; (6.18)

Т_ср.с = Т_ср.0(m₀ + 1),

где λ₀= nλ– интенсивность отказов нерезервированной системы; _λ – интенсивность отказов элемента; n – число элементов основной системы; T_cp.0 – среднее время безотказной работы нерезервированной системы; m₀ – число резервных элементов. В этом случае кратность резервирования

m = m₀ /n. (6.19)

Приведенные выше формулы (кроме (6.8), (6.11), (6.12)) могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последствий отказов.

Последствия отказов проявляются практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва.

Выражение (6.8) является основным при получении расчетных формул в случае учета влияния последействия отказов. При этом члены p(t– τ) и а_m(τ) должны быть записаны с учетом последствий отказов, вида резервирования и его кратности.

Элементы резервированных устройств в ряде случаев могут иметь два вида отказов – «обрыв» и «короткое замыкание». В этом случае вычислять вероятность безотказной работы следует, суммируя вероятности всех благоприятных (не приводящих к отказу) гипотез, т. е.

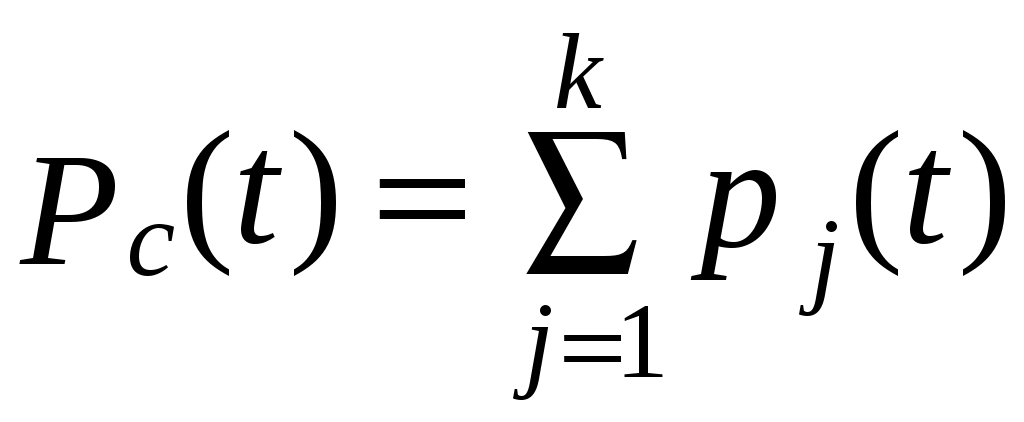, (6.20)

где p_j(t) – вероятность j-й благоприятной гипотезы, вычисленной с учетом двух видов отказав; k– число благоприятных гипотез.

При вычислениях p_j

---

(t) следует иметь в виду, что для элементов сложной системы справедливы выражения

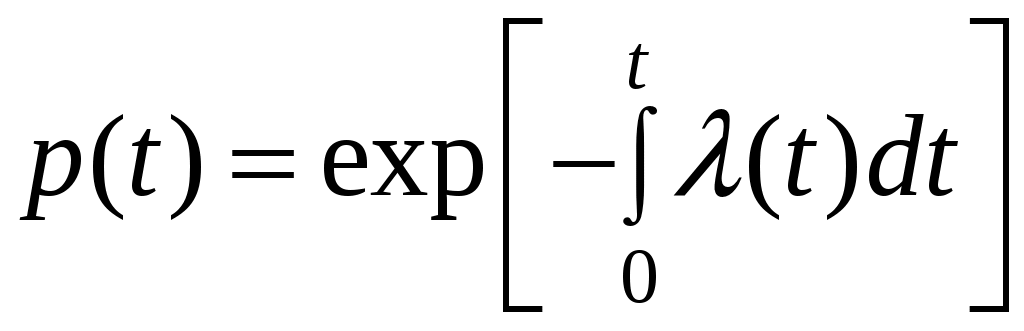, φ₀ + φ_з= 1, (6.21)

где (t) – интенсивность отказов элемента;φ₀,φ_з– вероятность возникновения «обрыва» и «короткого замыкания» соответственно.

При экспоненциальном законе надежности

_p(t)=e^-λt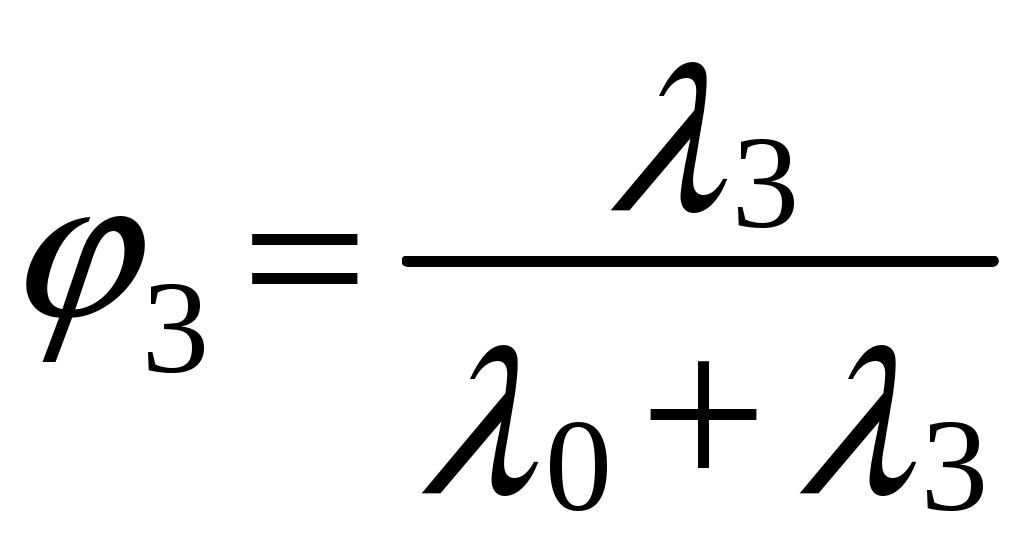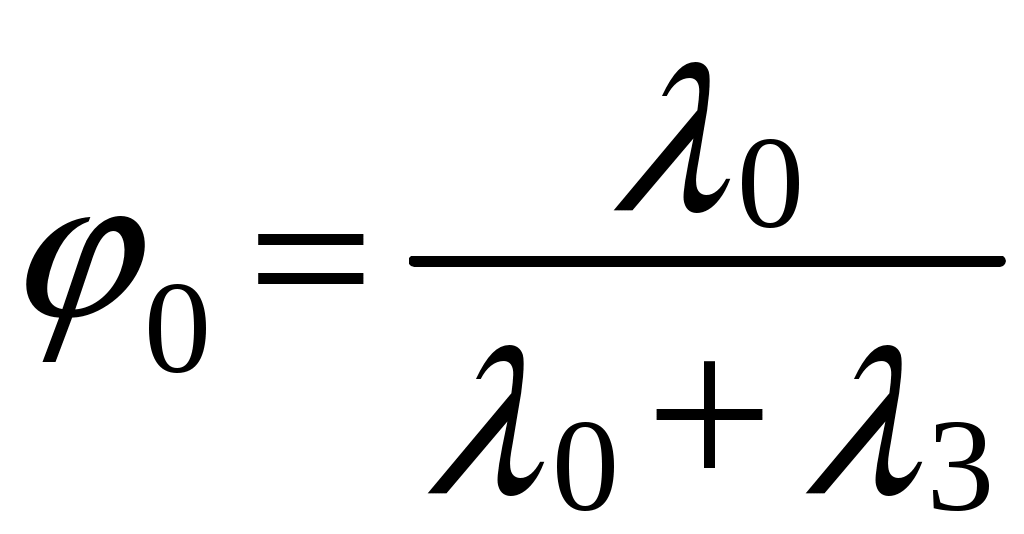_, , , (6.22)

где λ₀,λ₃ – интенсивность отказов элемента по «обрыву» и «короткому замыканию» соответственно.

Остальные количественные характеристики надежности в случае необходимости вычисляются через P_c(t) по известным аналитическим зависимостям, приведенным в главе 1.

Расчет надежности резервированных систем иногда полезно выполнять, используя схему «гибели» («чистого размножения»). В соответствии с этой схемой преобразование Лапласа вероятности возникновения п отказов вычисляется по формуле

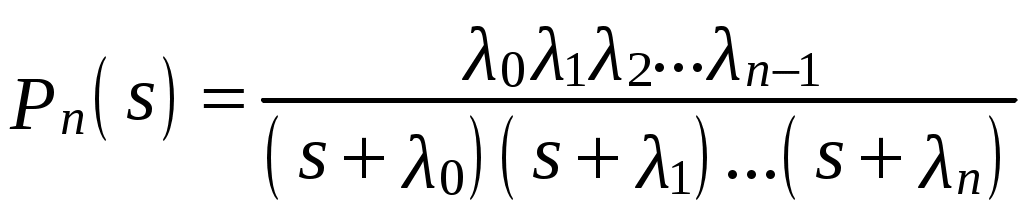. (6.23)

При неравных корнях знаменателя обратное преобразование Лапласа P_n(s) будет

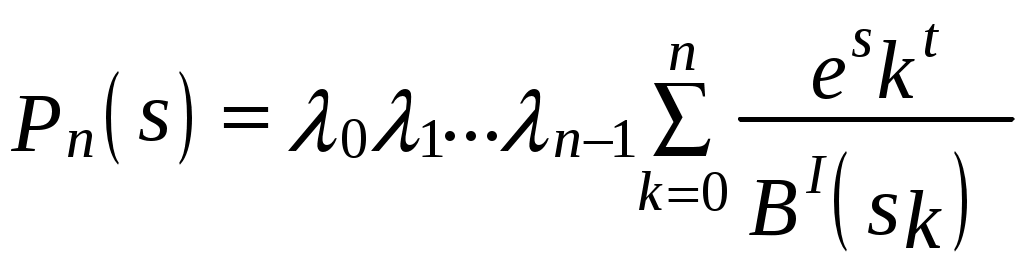. (6.24)

В формулах (6.23) и (6.24) приняты обозначения: λ₀ – интенсивность отказов системы до выхода из строя первого элемента; λ₁– интенсивность отказов системы в промежутке времени от момента отказа первого элемента до второго; λ₂ – интенсивность отказов системы в промежутке времени от момента отказа второго эле­мента до третьего и т. д.; п– число отказавших элементов; s_k= –λ_h – k-й корень знаменателя выражения (6.23); B'(s_k) – производная знаменателя в точке s_k .

При одинаковых опасностях отказов λ_i, т. е. λ₀= λ₁= λ₂ =…=λ_n, расчетные формулы имеют вид:

---

,

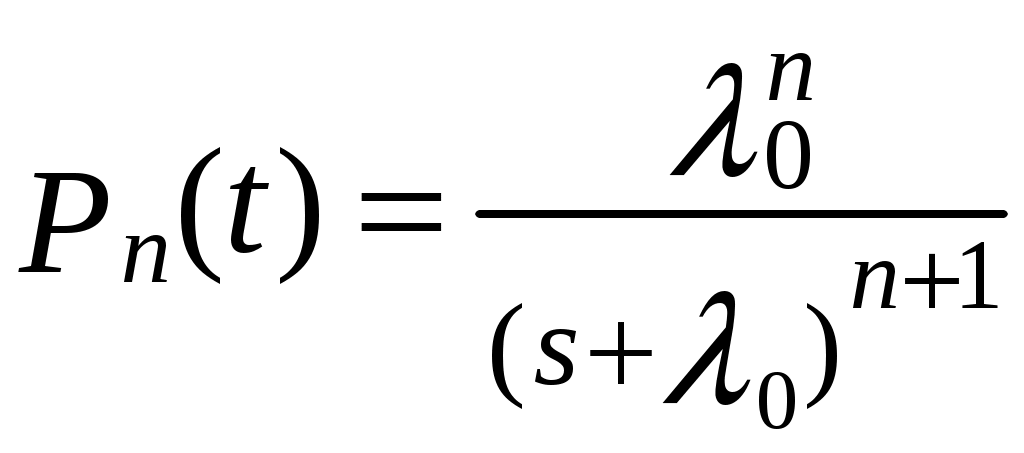
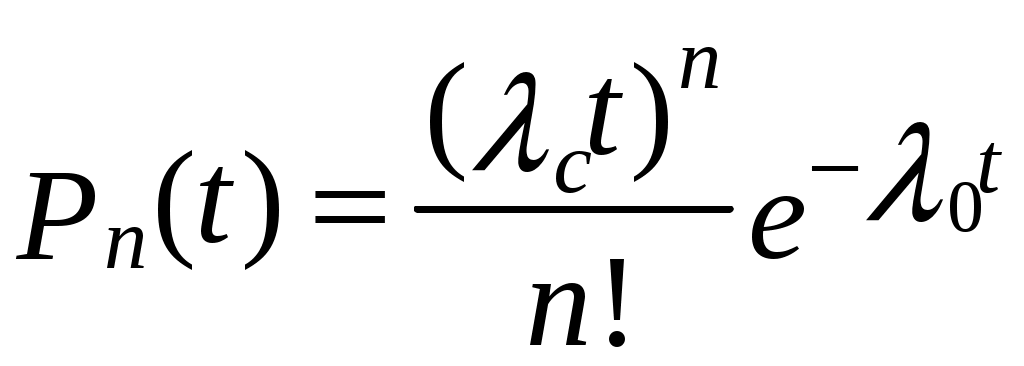. (6.25)

При расчетах надежности по формулам (6.23)–(6.25) следует помнить, что они не определяют вероятности безотказной работы (или вероятности отказа) резервированной системы, а определяют лишь вероятность i-го состояния системы, т е. вероятность того, что в системе откажут пэлементов. Для вычисления вероятности безотказной работы следует находить вероятности
0, 1, ..., n отказов, когда система еще находится в работоспособном состоянии (исправна), и суммировать полученные вероятности.

Среднее время безотказной работы системы при использовании схемы «гибели» вычисляется по формуле

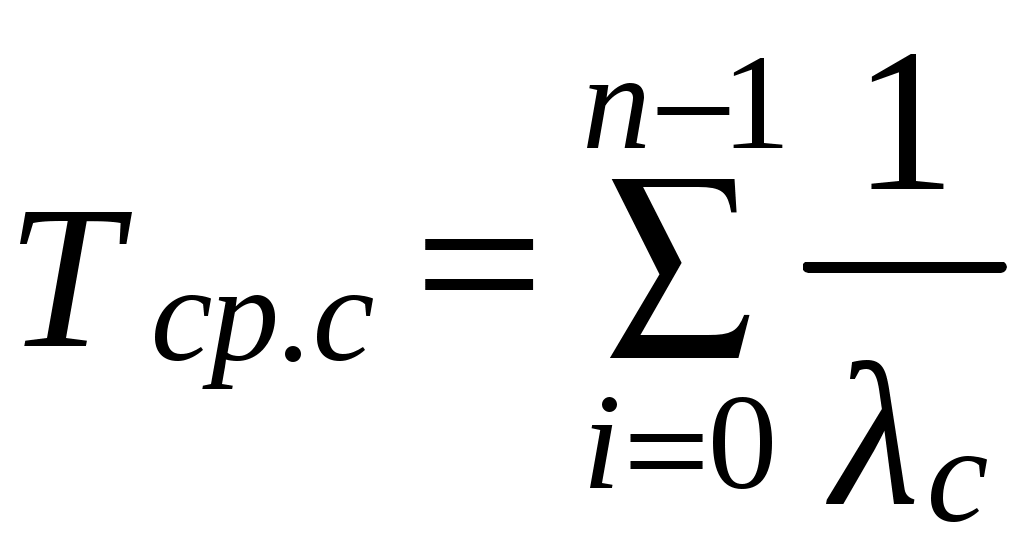, (6.26)

где λ_i– интенсивность отказов системы до выхода из строя i-го элемента.

При схемной реализации резервирования в ряде случаев конкретные технические решения не приводятся к логическим схемам расчёта надёжности (рис. 5.1, 5.2, 5.4, 5.5).

В таких случаях необходимо с целью получения аналитических выражений для количественных характеристик надежности использовать метод перебора благоприятных гипотез. Вероятность безотказной работы при этом вычисляется по выражению (6.20).

При анализе надежности резервированных устройств на этапе проектирования приходится сравнивать различные схемные решения. В этом случае за критерий качества резервирования принимается выигрыш надежности.

Выигрышем надежности называется отношение количественной характеристики надежности резервированного устройства к той же количественной характе­ристике нерезервированного устройства или устройства с другим видом резервирования.

Наиболее часто используются следующие критерии качества резервированных устройств: _G0(t)i – выигрыш надежности в течение времени t по вероятности отказов; _{G0(t) –} выигрыш надежности в течение времени t по вероятности безотказной работы; G_T – выигрыш надежности по среднему времени безотказной работы.

При резервировании элементов электроники (резисторов, конденсаторов, контактов реле, диодов и т. п.) всегда произведение интенсивности отказов элемента и времени его работы значительно меньше единицы, т. е. λt

---

1, поэтому при вычислении G_q(t)и G_q(p) целесообразно функции вида e^-kλt (экспоненциальный случай) разложить в ряд:

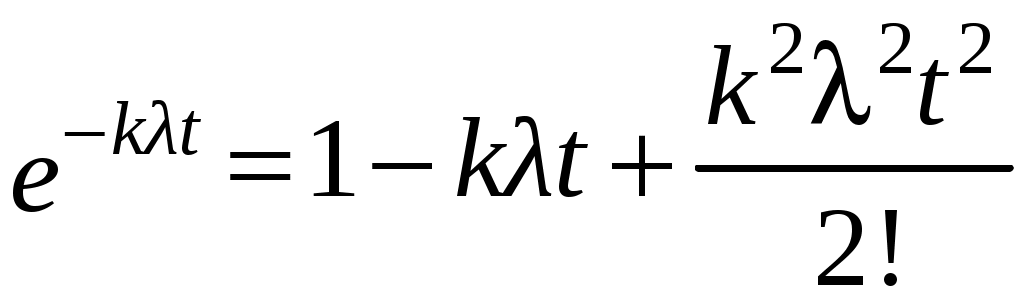(при небольшом k).

Если система исправна при отказе тэлементов, то необходимо брать не менее чем m + 2 членов разложения.

---