Файл: Учебное пособие в двух частях Часть Основы теории.doc

Пример 6.1. Дана система, схема расчета надежности которой изображена на рис. 6.2. Необходимо найти вероятность безотказной работы системы при известных вероятностях безотказной работы ее элементов (значе­ния вероятностей указаны на рисунке).

Рис. 6.2. Схема расчета надежности
Решение. На рис. 6.2 видно, что система состоит из двух (I и II) неравнонадежных устройств.

Устройство I состоит из четырех узлов: а– дублированного узла с постоянно включенным резервом, причем каждая часть узла состоит из трех последовательно соединенных (в смысле надежности) элементов расчета; б– дублированного узла по способу замещения; в– узла с одним нерезервированным элементом; г– резервированного узла с кратностью m = ¹/₂ (схе­ма группиро­вания).

Устройство II представляет собой нерезервированное устройство, надежность которого известна.

Так как оба устройства неравнонадежны, то на осно­вании формулы (6.3) имеем



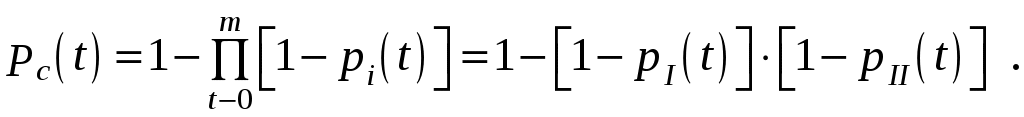
Определяется вероятность p_I(t). Вероятность безотказной работы устройства I равна произведению вероятностей безотказной работы всех узлов, т. е.

p_I(t) =р_а р_б р_в р_г.

В узле ачисло элементов основной и резервной цепи n = 3, а кратность резервирования т = 1. Тогда на осно­вании формулы (6.1)



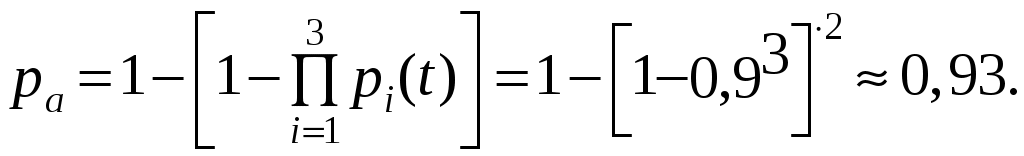
В узле бкратность общего резервирования замеще­нием т=1, тогда на основании формулы (6.9) получается:

.

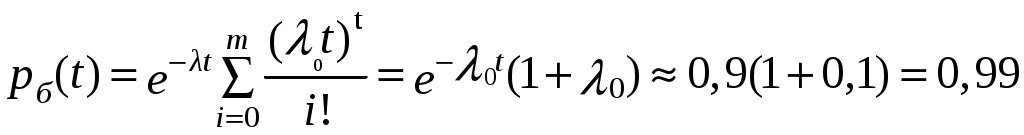В узле гприменено резервирование с дробной крат­ностью, когда общее число основных и резервных систем l = 3,число систем, необходимых для нормальной ра­боты, h= 2.

Тогда на основании формулы (6.14) вероятность безотказной работы устройства I будет

р_х= р_а р_б р_в р = 0,93 · 0,99 · 0,97 · 0,972 ≈ 0,868,

а вероятность безотказной работы резервирован­ной системы будет

---

P₀ = l – (l – p_I) (1– р_II) –1– (1 – 0,868) (1– 0,9) = 0,987.

Пример 6.2. Вероятность безотказной работы преоб­разователя постоянного тока в переменный в течение t= 1000 ч равна 0,95, т. е. Р (1000) = 0,95. Для повышения надежности системы электроснабжения на объек­те имеется такой же преобразователь, который включа­ется в работу при отказе первого. Требуется рассчитать вероятность безотказной работы и среднюю наработку до первого отказа системы, состоящей из двух преобра­зователей, а также построить зависимости от времени частоты отказов f_c(t)и интенсивности отказов _c(t) си­стемы.

Решение. Из условия задачи видно, что имеет ме­сто общее резервирование замещением кратности т = 1. Тогда на основании формулы (6.9) полу­чается

.

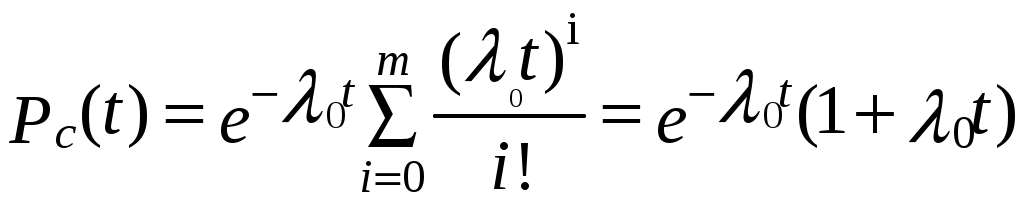Из условия задачи = 0,95, тогда λ₀(t) ≈ 0,05. Под­становка значения Р(1000) и значения λ₀(t)в выражение для Р_с(t) позволяет получить

.

Средняя наработка до первого отказа системы на основании формулы (6.10)

.

Так как в течение времени t= 1000 чиλ₀t= 0,05, то 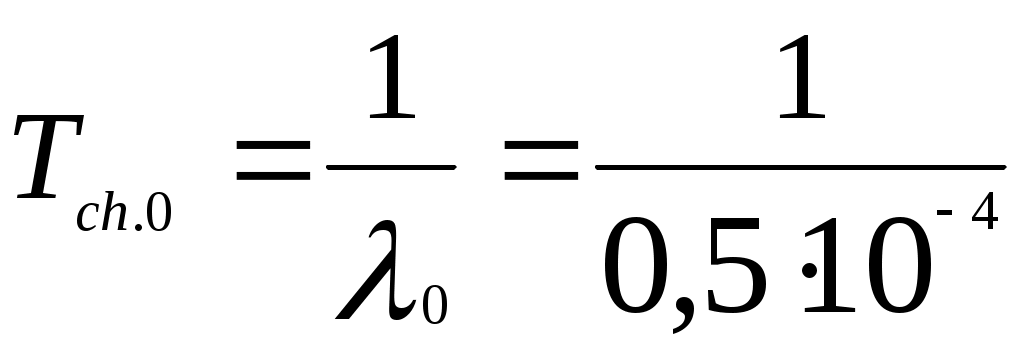= 0,5·10^–4 ч^–1,а средняя наработка до первого отказа нерезервированного преобразова­теля = 20 000 ч.

Тогда средняя наработка до первого отказа резерви­рованной системы Т_ср.с = 2 Т_ср.0 = 40 000 ч.

Для построения графиков f_c(t) и λ_c(t) находятся ана­литические выражения этих функций по известной вероятности безотказной работы системы:

,

.

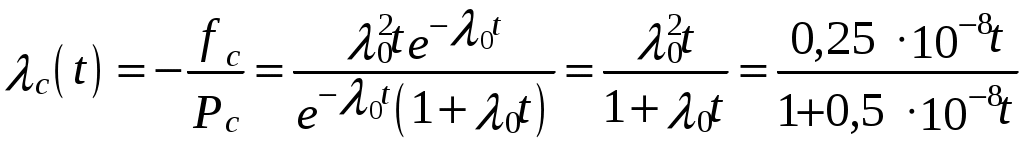Графики f_c(t)и λ_c(t) приведены на рис. 6.3.



Рис. 6.3. Зависимость f

---

_си λ_cот t

Количественно повышение надежности системы в результате резервирования или применения высоконадежных элементов можно оценить по коэффициенту выигрыша надежности, определяемому как отношение показателя надежности до и после преобразования системы. Например, для системы из n последовательно соединенных элементов после резервирования одного из элементов (k-го) аналогичным по надежности элементом коэффициент выигрыша надежности по вероятности безотказной работы составит:

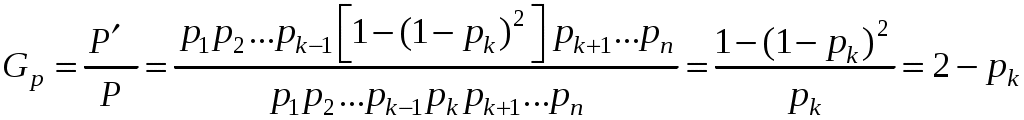, (6.27)

где Р^' – вероятность безотказной работы резервированной системы;

Р –вероятность безотказной работы нерезервированной системы.

Из формулы (6.27) следует, что эффективность резервирования (или другого приема повышения надежности) тем больше, чем меньше надежность резервируемого элемента (при , при ).

Следовательно, при структурном резервировании наибольшего эффекта можно добиться при резервировании самых ненадежных элементов (или групп элементов).

В общем случае при выборе элемента (или группы элементов) для повышения надежности или резервирования необходимо исходить из условия обеспечения при этом наилучшего результата.

6.3. Замечания к расчетам
надежности систем с резервированием

Расчет количественных характеристик надежности систем с резервированием отдельных элементов или групп элементов во многом определяется видом резервирования. Здесь рассматриваются схемы расчетов для самых распространенных случаев простого резервирования, к которым путем преобразований может быть приведена и структура смешанного резервирования. При этом расчетные зависимости получены без учета надежности переключающих устройств, обеспечивающих перераспределение нагрузки между основными и резервными элементами (т. е. для «идеальных» переключателей). В реальных условиях введение переключателей в структурную схему необходимо учитывать и в расчете надежности систем.

---

Расчёт систем с нагруженным резервированием осуществляется по формулам последовательного и параллельного соединения элементов аналогично расчету комбинированных систем. При этом считается, что резервные элементы работают в режиме основных как до, так и после их отказа, поэтому надёжность резервных элементов не зависит от момента их перехода из резервного состояния в основное и равна надежности основных элементов.

При нагруженном резервировании резервные элементы расходуют свой ресурс, имеют одинаковое распределение наработок до отказа и интенсивность отказов основных λ₀ и резервных λ_р элементов одинакова (λ₀ = λ_р).

При нагруженном резервировании различие между основными и резервными элементами часто условное. Для обеспечения нормальной работы (сохранения работоспособности) необходимо, чтобы число работоспособных элементов не становилось меньше минимально необходимого.

Кратность резервирования может быть определена несколько иначе, чем в п. 6.6.1.

Пусть n – число однотипных элементов в системе; r – число элементов, необходимых для функционирования системы.

Кратность резервирования – соотношение между общим числом однотипных элементов и элементов, необходимых для работы системы:

k = (n–r)/r.

Кратность резервирования может быть целой, если r= 1, или дробной, если r > 1.

Для системы с последовательным соединением n элементов (рис. 5.1) при общем резервировании с кратностью k (рис. 6.4, а)

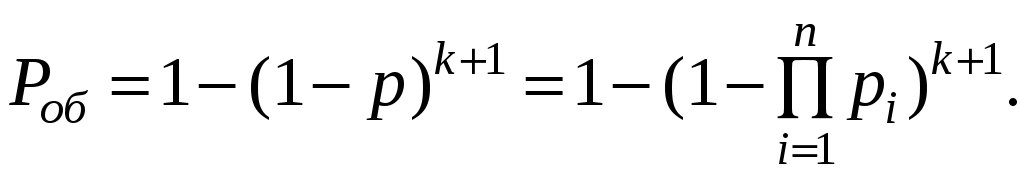(6.28)

Приведенная формула (6.28) идентична формуле (6.1).

В частности, при дублировании (k= 1)

. (6.29)

При раздельном резервировании (рис. 6.4, б)

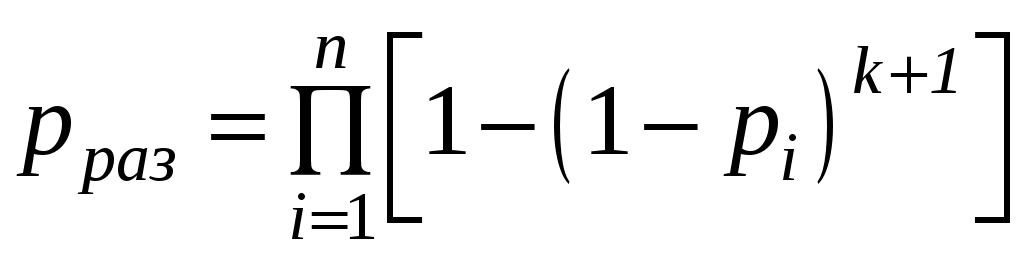, (6.30)

а при раздельном дублировании (k= 1)

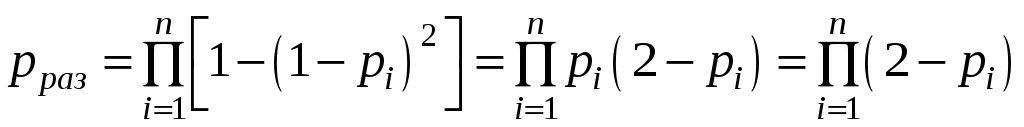. (6.31)



а) б)

Рис. 6.4. Общее (а) и раздельное (б) нагруженное резервирование
Тогда коэффициенты выигрыша надежности по вероятности безотказной работы при дублировании запишутся в виде:

---

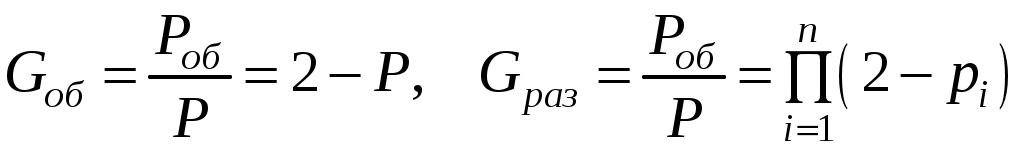, (6.32)

откуда следует, что раздельное резервирование эффективнее общего (например, для системы из трех одинаковых элементов при , G = 1,33.

При ненагруженном резервировании резервные элементы последовательно включаются в работу при отказе основного, затем первого резервного и т. д. (рис. 6.5), поэтому надежность резервных элементов зависит от момента их перехода в основное состояние. При ненагруженном резервированиирезервные элементы не подвергаются нагрузке, их показатели надежности не изменяются и они не могут отказать за время нахождения в резерве, т. е. интенсивность отказов резервных элементов λ_р = 0.

Такое резервирование в различных ТС встречается наиболее часто, так как по сути оно аналогично замене отказавших элементов и узлов на запасные.


Рис. 6.5. Ненагруженное резервирование Рис. 6.6. Скользящее резервирование
Если резервные элементы до их включения абсолютно надежны, то для системы с ненагруженным резервированием кратности k(всего элементов k+ 1)

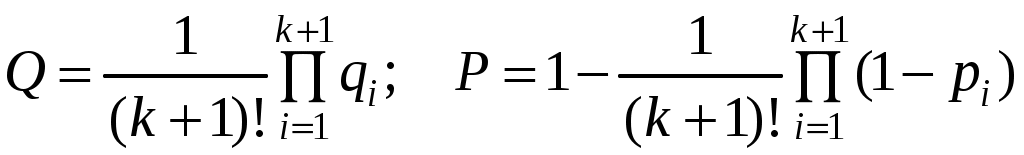, (6.33)

т. е. вероятность отказа в (k+1)! раз меньше, чем при нагруженном (параллельном соединении, см. формулу (6.35)).

Для идентичных (одинаковых) по надежности основного и резервного элементов

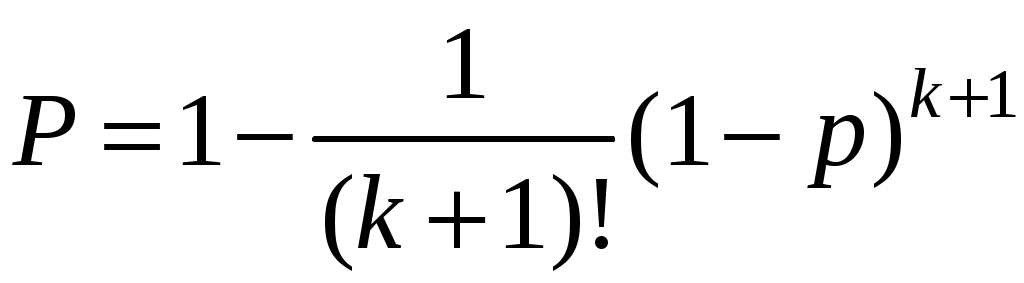. (6.34)

При экспоненциальном распределении наработки (простейшем потоке отказов) в случае можно воспользоваться приближенной формулой

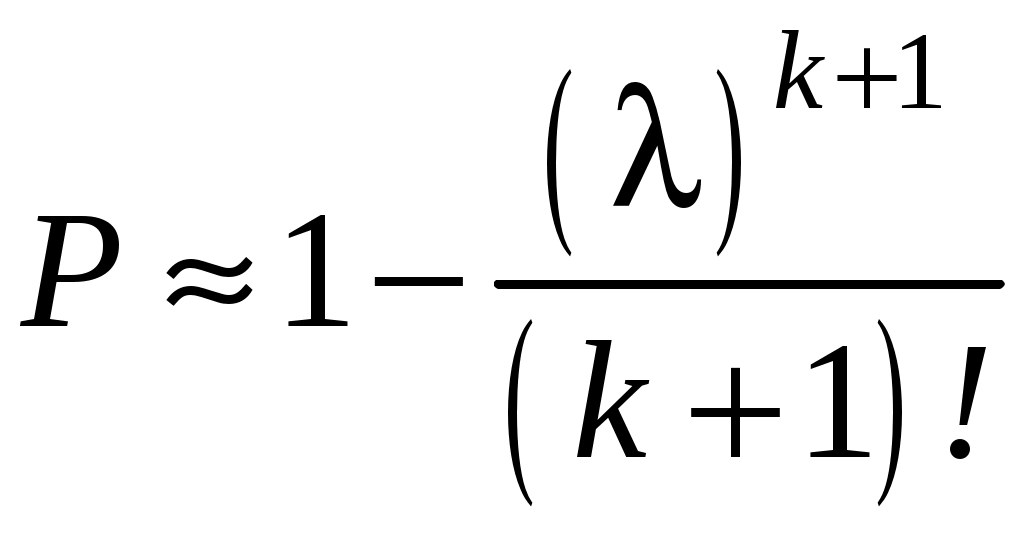. (6.35)

При ненагруженном резервировании средняя наработка на отказ

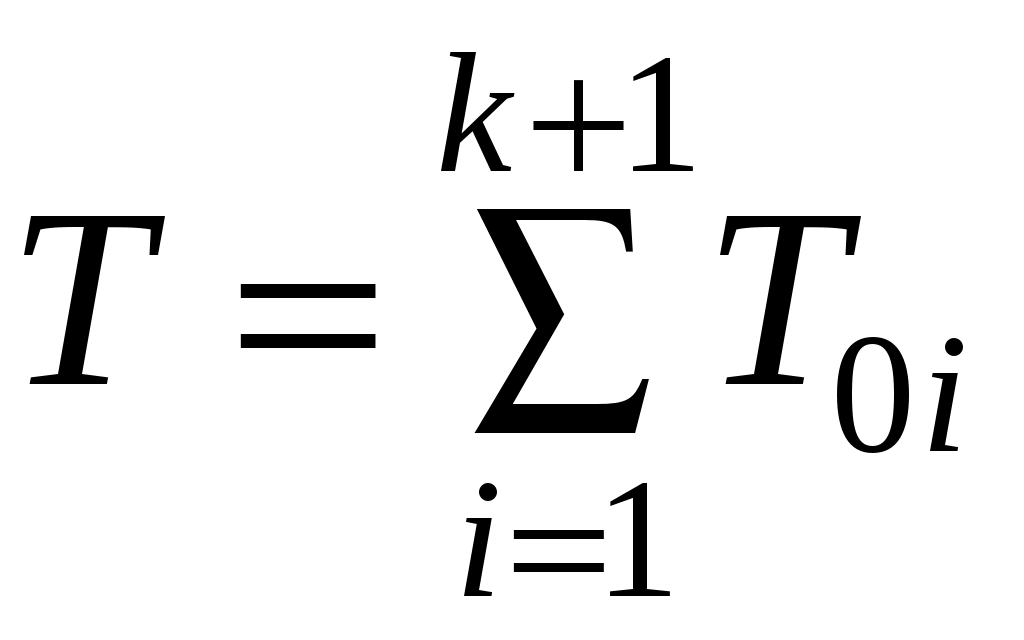, (6.36)

а для идентичных элементов T₀= nT_0i .

Примеры ненагруженного резервирования (рис. 6.7):

---