ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 964
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
На рис. 3.3 приведена графическая интерпретация перечисленных показателей, при этом:
t0 = 0 – начало эксплуатации;
t1, t5 – моменты отключения по технологическим причинам;
t2, t4, t6, t8 – моменты включения объекта;
t3, t7 – моменты вывода объекта в ремонт, соответственно, средний и капитальный;
t9 – момент прекращения эксплуатации;
t10– момент отказа объекта.
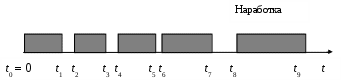
рис. 3.3. Схема эксплуатации объекта
Технический ресурс (наработка до отказа):
ТР = t1+ (t3 – t2) + (t5 – t4) + (t7 – t6) + (t10 – t8).(3.34)
Назначенный ресурс:
Тн.р = t1 + (t3 – t2) + (t5 – t4) + (t7 – t6) + (t9 –t8). (3.35)
Срок службы объектаТсл= t10.
Для большинства объектов в качестве критерия долговечности чаще всего используется технический ресурс.
Средний ресурс Тр.ср (средний срок службы Тсл.ср) – среднее значение ресурса (срока службы) совокупности объектов одного типа, размера и использования:
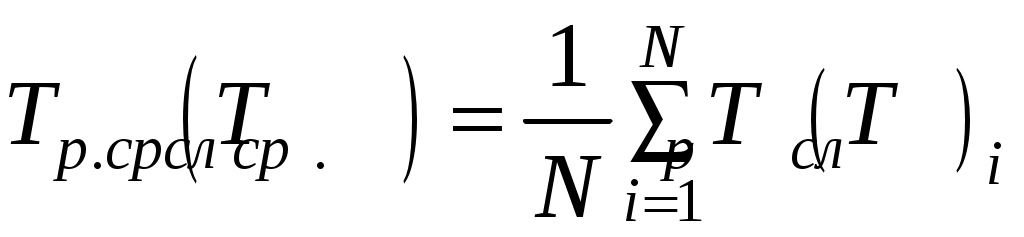 , (3.36)
, (3.36)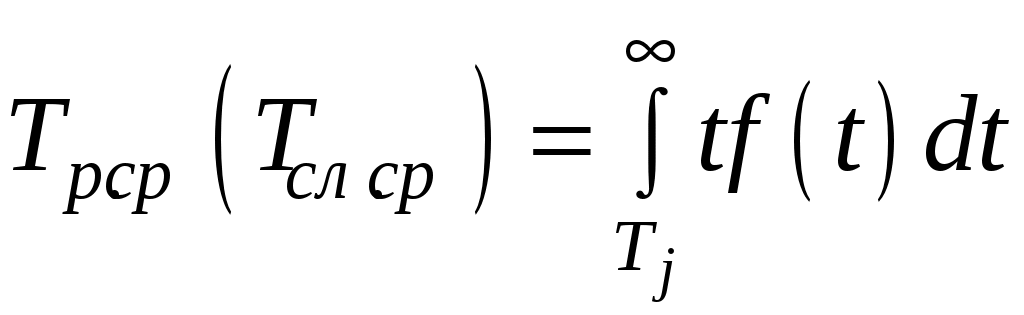 . (3.37)
. (3.37)Гамма-процентный ресурс Тγ – наработка, с течением которой изделие не достигает предела состояния с заданной вероятностью :
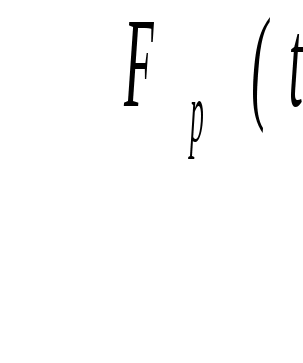
рис. 3.4. Функции F(Tγ) и fp(t)
Гамма-процентный ресурс Т= 90 % означает, что данное изделие проработает до своего предельного состояния с вероятностью более 90 % либо выйдет из строя с вероятностью 10 %.
Пример 3.3. Для протяжного станка задан гамма-процентный ресурс
Т = 99 %. Определить необходимый показатель интенсивности отказов, время эксплуатации (срок службы) Т = 12 000 ч.
Решение:
Р(t) = e–t;
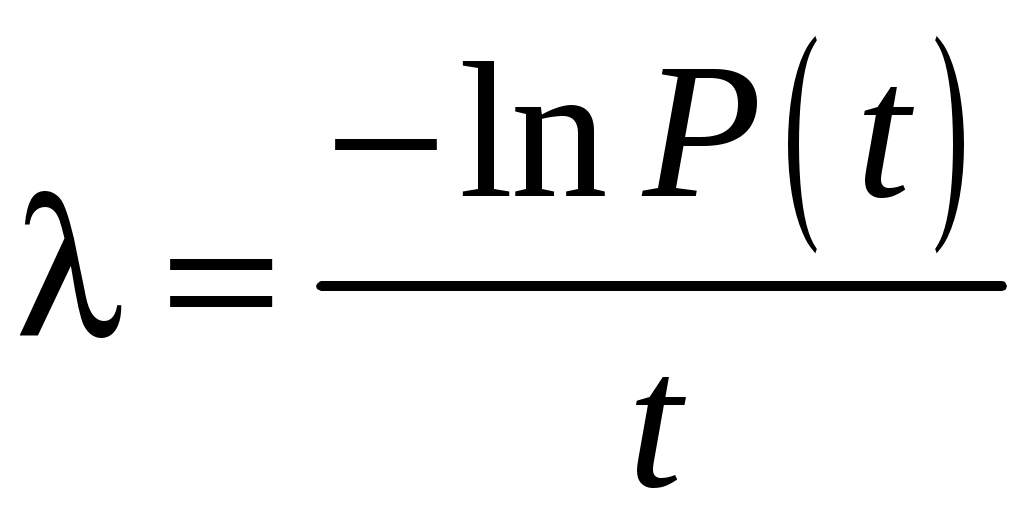
; Р(t) = 0,99;
Пример 3.4. Наработка до отказа t для 10 персональных компьютеров составила в часах: 21, 42, 68, 36, 18, 49, 16, 22, 74, 18. Вычислить надёжность персонального компьютера в течение 40 ч и определить интенсивность отказов в период между 20 и 50 ч работы и среднюю наработку до отказа.
Решение:
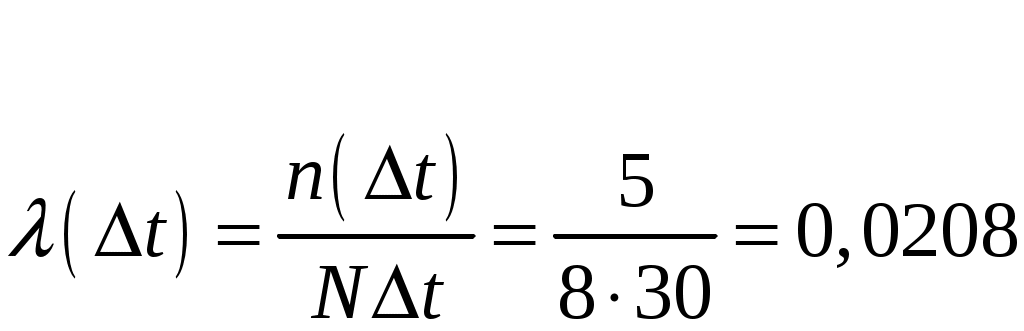
ч–1.
Считается, что компьютеры работают в течение периода нормальной эксплуатации, для которого выполняются условия:
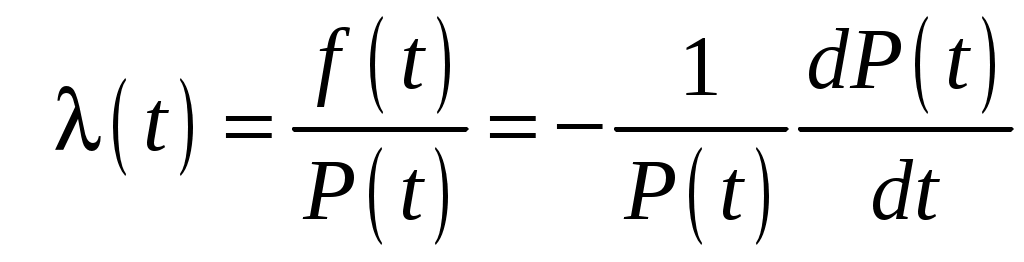 ,
,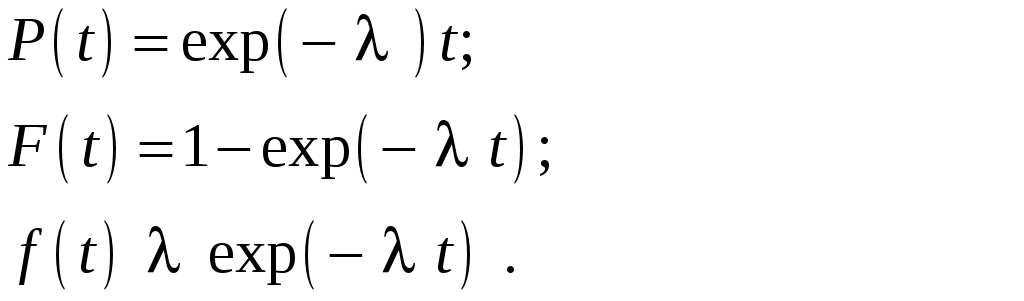
При
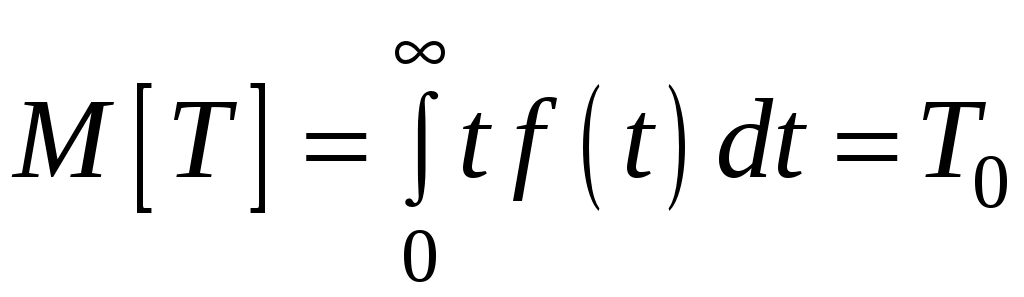 .
.Значение Т0 находят путём подстановки f(t) в последнее уравнение:
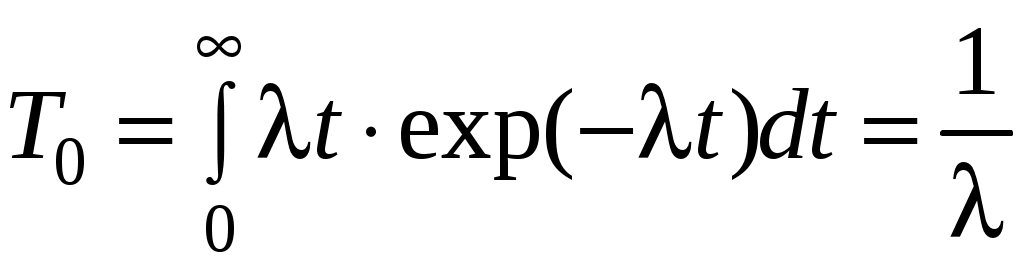 ч;
ч;3.5. Показатели сохраняемости объектов
Срок сохраняемости – календарная продолжительность хранения (транспортирования) объекта, в течение которой и в дальнейшем сохраняются значения показателей безотказности и долговечности в установленных пределах.
Средний срок сохраняемости
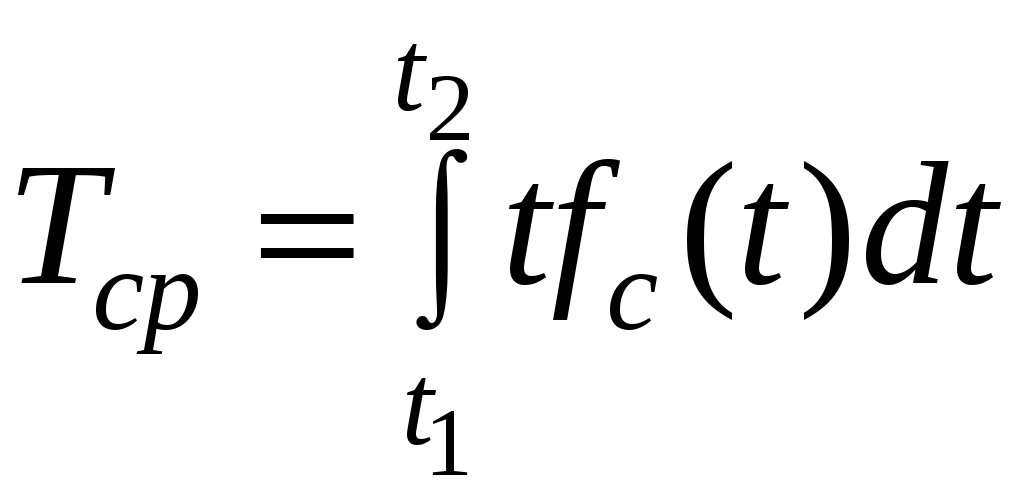 . (3.39)
. (3.39)Гамма-процентный срок сохраняемости – календарная продолжительность хранения (транспортирования), в течение и после которой показатели безотказности и долговечности объекта не выйдут за установленные пределы с вероятностью , выраженной в процентах.
Назначенный срок хранения в заданных условиях – срок хранения, по истечении которого применение объекта по назначению не допускается, независимо от его технического состояния.
3.6. Экономические показатели надёжности объектов
Экономические показатели надёжности позволяют оценить затраты на использование техники, ремонтного оборудования, обслуживание и сделать вывод.Коэффициент экономичности:
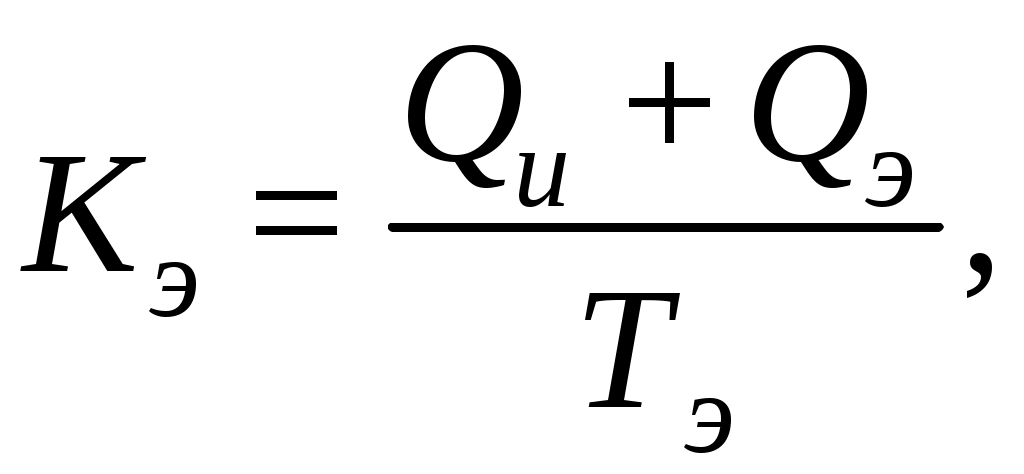 (3.40)
(3.40)где Qи – цена изготовления объекта;
Qэ– затраты на эксплуатацию (ремонт, обслуживание, потери от простоя);
Тэ – срок эксплуатации.
Цена надёжности:
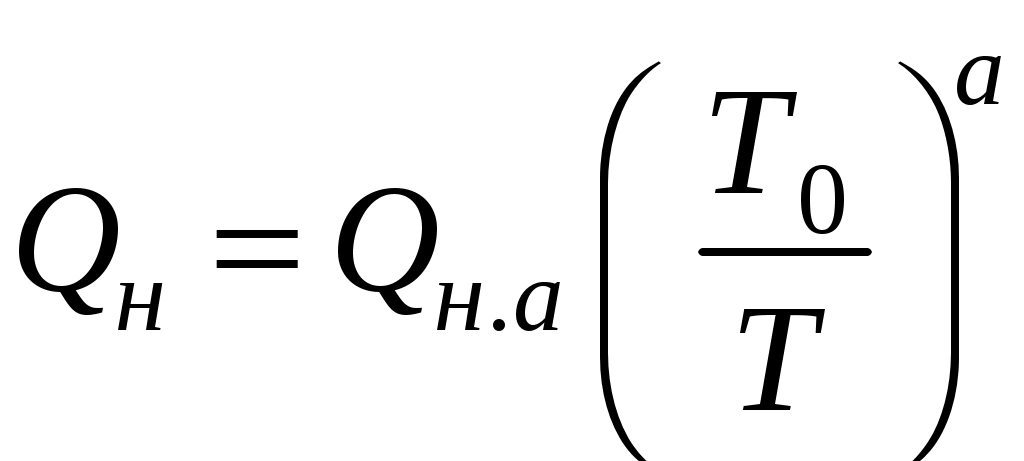 , (3.41)
, (3.41)где Qн.а – цена надёжности аналога;
Т0, Т – наработка на отказ прототипа и проектируемого изделия;
а – эмпирический показатель, характеризующий уровень прогрессивности производства с точки зрения возможности заданного повышения надёжности изделия, а = 0,5…1,5.
3.7. Комплексные показатели надёжности объектов
Коэффициент готовности КГ – вероятность работоспособного состояния восстанавливаемого объекта:
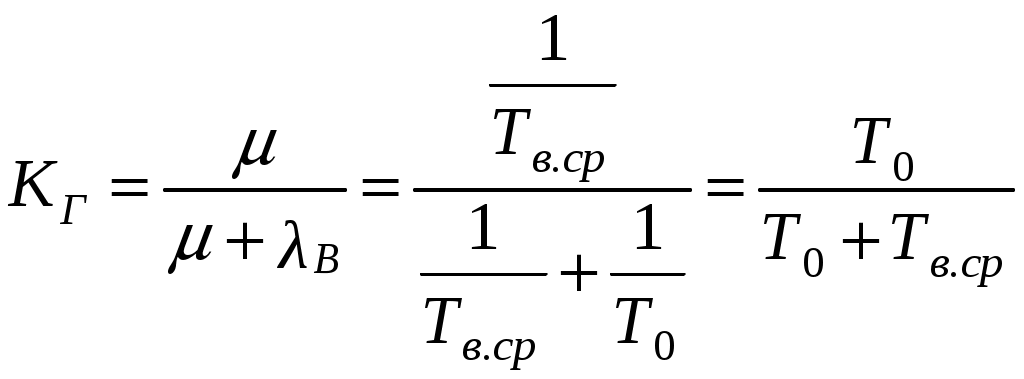 , (3.42)
, (3.42)где В – интенсивность восстановления;
μ – параметр потока отказов.
Коэффициент оперативной готовности КОГ – предусматривает необходимость внезапного использования объекта, после чего требуется безотказное выполнение объектом основной функции в течение времени оперативной готовности ТОГ:
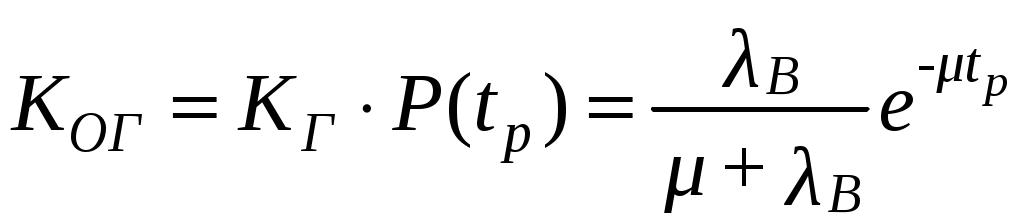 . (3.43)
. (3.43)Коэффициент технического использования КТИ:
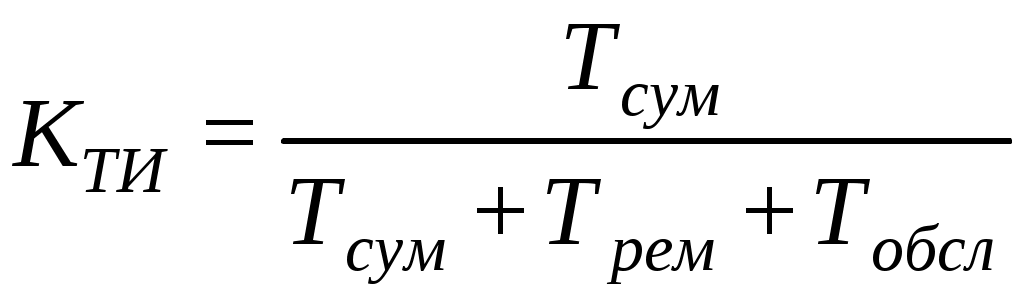 , (3.44)
, (3.44)где Тсум – суммарное время пребывания объекта в работоспособном состоянии;
Трем – время нахождения объекта в ремонте;
Тобсл – время нахождения объекта в обслуживании.
Коэффициент простоя КП – вероятность нахождения объекта в неработоспособном состоянии:
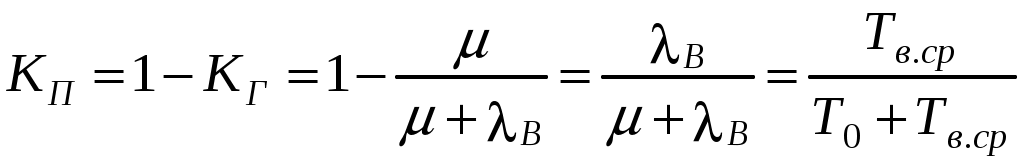
. (3.45)
Контрольные вопросы
1. Дайте определение вероятности безотказной работы объекта и пояснить ее смысл.
2. Укажите отличия вероятности безотказной работы объекта при наработке t от вероятности безотказной работы в интервале наработки [t, t + Δt].
3. Дайте графическую интерпретацию понятий вероятности безотказной работы и вероятности отказов.
4. Дайте определение интенсивности отказов.
5. По результатам испытаний N = 50 однотипных элементов определите показатели безотказности для заданных наработок ti, если известно, что число отказавших элементов n(ti) к моментам наработки составляет:
n(t1) = 2, t1 = 200 ч,
n(t2) = 5, t2 = 300 ч,
n(t3) = 7, t3 = 400 ч,
n(t4) = 10, t4 = 500 ч,
n(t5)= 15, t5 = 600 ч.
6. Какие показатели надежности восстанавливаемых объектов существуют?
7. Что такое поток отказов?
8. Как можно посчитать вероятность безотказной работы восстанавливаемого объекта?
9. Перечислите показатели долговечности.
10. Перечислите показатели сохраняемости.
11. Зачем нужно знать экономические показатели надёжности?
12. Перечислите экономические показатели надёжности.
13. Перечислите комплексные показатели надёжности.
4. Математические модели
теории надёжности
4.1. Статистическая обработка результатов испытаний
Для решения задач по оценке надёжности и прогнозированию работоспособности объекта необходимо иметь математическую модель, которая представлена аналитическими выражениями одного из показателей P(t), f(t) или
λ(t). Основной путь для получения модели состоит в проведении испытаний, вычислении статистических оценок и их аппроксимации аналитическими функциями.
Возникает необходимость выяснить, как изменяется безотказность объектов при их эксплуатации, что позволит классифицировать модели и определить возможности их применения.
Опыт эксплуатации показывает, что изменение интенсивности отказов λ(t) подавляющего большинства объектов описывается U-образной кривой (рис. 4.1).
λ(t)
наработка t
ед. наработки –1
Период
наработки
Период нормальной эксплуатации
Период
старения

Рис. 4.1. Кривая изменения интенсивности отказов
Кривую можно условно разделить на три характерных участка: первый – период приработки, второй – период нормальной эксплуатации, третий – период старения объекта.
Период приработки объекта имеет повышенную интенсивность отказов, вызванную приработочными отказами, обусловленными дефектами производства, монтажа, наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем.
В период нормальной эксплуатации интенсивность отказов уменьшается и практически остается постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего, из-за несоблюдения условий эксплуатации, случайных изменений нагрузки, неблагоприятных внешних факторов
и т. п. Именно этот период соответствует основному времени эксплуатации объекта.
Возрастание интенсивности отказов относится к периоду старения объекта и вызвано увеличением числа отказов от износа, старения и других причин, связанных с длительной эксплуатацией.
Вид аналитической функции, описывающей изменение показателей надежности P(t), f(t) или λ(t), определяет закон распределения случайной величины, который выбирается в зависимости от свойств объекта, условий его работы и характера отказов.
4.2. Надёжность объектов
в период нормальной эксплуатации
Надёжность в этот период характеризуется внезапными отказами, так как постоянные отказы ещё не проявляются. Внезапные отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность, не зависящую от возраста изделия:
где Т – средняя наработка до отказа (обычно в часах),
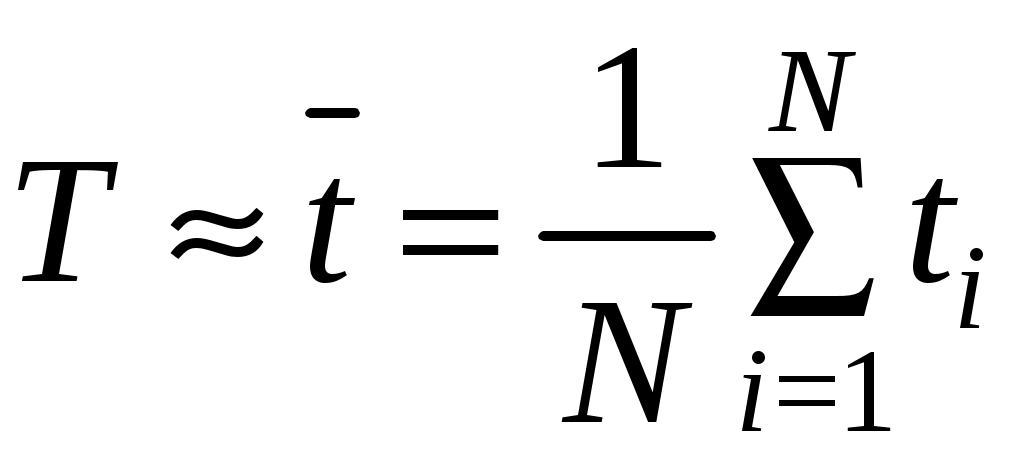 , (4.2)
, (4.2)где ti – наработка до отказаi-го изделия; N– общее число наблюдений.
Вероятность безотказной работы: