∆ДВК = ∑(∆Уд_i × ДВК_i0) = [(+10) × 15 + (-10) × 10] ∕ 100 = +0,5%

уровня доходности отдельных видов инвестиций

∆ДВК = ∑(Уд_i1 × ∆ДВК_i)= (90 × 1 + 10 × 0) ∕ 100 = +0,9%.

Таблица 23.6

Анализ эффективности использования долгосрочных финансовых вложений

Показатель	Прошлый год	Отчетный год	Изменение
Сумма долгосрочных финансовых вложений, тыс. руб.	2500	3000	+500
В том числе:
в акции	2000	2700	+700
в облигации	500	300	-200
Удельный вес, % :
акций	80,0	90	+ 10
облигаций	20,0	10	-10
Доход, тыс. руб.:
от акций	300	432	+132
от облигаций	50	30	-20
Доходность долгосрочных финансовых инвестиций, %	14	15,4	+ 1,4
В том числе:
акций	15	16	+ 1
облигаций	10	10	—

---

Доходность ценных бумаг необходимо сравнивать также с так называемым альтернативным (гарантированным) доходом, в качестве которого принимается ставка рефинансирования, или процент, получаемый по государственным облигациям или казначейским обязательствам.

Оценка и прогнозирование экономической эффективности отдельных финансовых инструментов может производиться с помощью как абсолютных, так иотносительных показателей. В первом случае определяется текущая рыночная цена финансового инструмента, по которой его можно приобрести, и внутренняя его стоимость исходя из субъективной оценки каждого инвестора. Во втором случае рассчитывается относительная его доходность.

Различие между ценой и стоимостью финансового актива состоит в том, что цена - это объективный декларированный Показатель, а внутренняя стоимость - расчетный показатель, результат собственного субъективного подхода инвестора.

Текущая внутренняя стоимость любой ценной бумаги в общем виде может быть рассчитана по формуле

PV_ф.и= ,

где РV_ф.u - реальная текущая стоимость финансового инструмента;

СF_n- ожидаемый возвратный денежный поток в п-м периоде;

d - ожидаемая или требуемая норма доходности по финансовому инструменту;

п - число периодов получения доходов.

Подставляя в данную формулу значения предполагаемых денежных поступлений, доходности и продолжительности периода прогнозирования, можно рассчитать текущую стоимость любого финансового инструмента.

Если фактическая сумма инвестиционных затрат (рыночная стоимость) по финансовому инструменту будет превышать его текущую стоимость, то инвестору нет смысла приобретать его на рынке, так как он получит прибыль меньше ожидаемой. Напротив, держателю этой ценной бумаги выгодно продать ее в данных условиях.

Как видно из вышеприведенной формулы, текущая стоимость финансового инструмента зависит от трех основных факторов: ожидаемых денежных поступлений, продолжительности прогнозируемого периода получения доходов и требуемой нормы прибыли. Горизонт прогнозирования зависит от вида ценных бумаг. Для облигаций и привилегированных акций он обычно ограничен, а для обыкновенных акций равен бесконечности.

---

Требуемая норма прибыли, закладываемая инвестором в алгоритм расчета в качестве дисконта, отражает, как правило, доходность альтернативных данному инвестору вариантов вложения капитала. Это может быть размер процентной ставки по банковским депозитам, уровень процента по правительственным облигациям и т.д.

Особенности формирования возвратного денежного потока по отдельным видам ценных бумаг обусловливают разнообразие моделей определения их текущей стоимости.

Базисная модель оценки текущей стоимости облигаций с периодической выплатой процентов выглядит следующим образом:

,

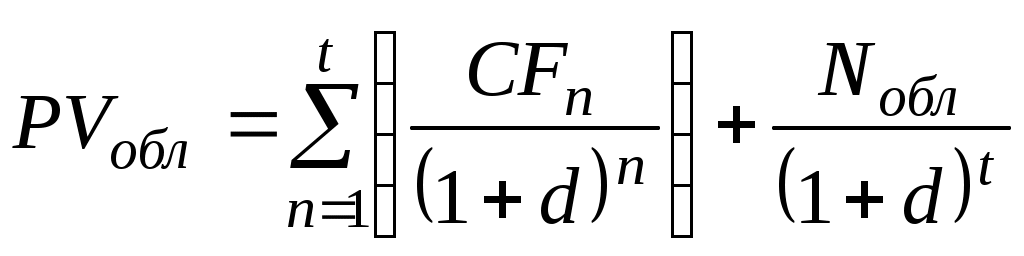где РV_обл - текущая стоимость облигаций с периодической выплатой процентов;

СF_n - сумма полученного процента в каждом периоде (произведение номинала облигации на объявленную ставку процента (N_оδл × k);

N_обл - номинал облигации, погашаемый в конце срока ее обращения (t);

k - годовая купонная ставка процента.

Пример. Требуется определить текущую стоимость трехлетней облигации, номинал которой 1000 руб. и с купонной ставкой 8% годовых, выплачиваемых раз в год, если норма дисконта (рыночная ставка) равна 12% годовых.

= 904 руб.

Следовательно, норма доходности в 12% будет обеспечена при покупке облигации по цене, приблизительно равной 900 руб.

Если рыночная норма доходности равна 6%, то текущая стоимость облигации будет равна:

= 1053 руб.

Отсюда видно, что текущая стоимость облигации зависит от величины рыночной процентной ставки и срока до погашения. Если d > k, то текущая стоимость облигации будет меньше номинала, т.е. облигация будет продаваться с дисконтом. Если d < k, то текущая стоимость облигации будет больше номинала, т.е. облигация продается с премией. Если d = k, то текущая стоимость облигации равна ее номиналу.

Доход по купонным облигациям состоит, во-первых, из периодических выплат процентов (купонов), во-вторых, из курсовой разности между рыночной и номинальной ценой облигации.

Поэтому для характеристики доходности купонных облигаций используется несколько показателей:

---

а) купонная доходность, ставка которой объявляется при выпуске облигаций;

б) текущая доходность, представляющая собой отношение процентного дохода к цене покупки облигации:

Y = = 8,51%,

где N_обл- номинал облигации;

k - купонная ставка процента;

Р - цена покупки облигации;

в) доходность к погашению:

= 10,3%.

где F - цена погашения;

Р - цена покупки,

CF - сумма годового купонного дохода по облигации,

п - число лет до погашения.

Модель оценки текущей стоимости облигаций с выплатой всей суммы процентов при ее погашении:

PV = = 882,6 руб.,

где N × k × п - сумма процентов по облигации, выплачиваемая в конце срока ее обращения.

Модель оценки текущей стоимости облигаций, реализуемых с дисконтом без выплаты процентов

=711,7

Модель доходности дисконтных облигаций:

по эффективной ставке процента:

YTM = ;

по ставке простых процентов:

YTM = ,

где Р_k - курс облигации (отношение цены покупки к номинальной стоимости облигации);

Т - количество календарных дней в году;

t - количество дней до погашения облигации.

Предположим, требуется определить уровень доходности облигаций к погашению, если цена покупки - 850 руб., цена выкупа (номинал) - 1(300 руб., срок обращения облигации - 90 дней:

по эффективной ставке процента:

YТМ = – 1 = 91,5%;

по ставке простых процентов:

YТМ =

---

=70,6%.

Для оценки текущей стоимости акции при ее использовании в течение неопределенного периода времени используют обычно следующую модель:

PV_акц = ,

где РV_αкц - текущая стоимость акции, используемой в течение неопределенного периода времени;

D_t- предполагаемая к получению сумма дивидендов в t-мпериоде;

d - альтернативная норма доходности в виде десятичной дроби;

t - число периодов, включенных в расчет.

Текущая стоимость акций со стабильным уровнем дивидендов определяется отношением суммы годового дивиденда к рыночной норме доходности:

РV_акц = D_i∕ d = 200 ∕ 0,15 = 1333 руб.

Для определения текущей стоимости акций, используемых в течение определенного срока, используется следующая модель:

РV_акц = ,

где КС - курсовая стоимость акции в конце периода ее реализации;

п - число периодов использования акции.

Пример. Номинальная стоимость акции - 1000 руб., уровень дивидендов - 20%, ожидаемая курсовая стоимость акции в конце периода ее реализации - 1100 руб., рыночная норма доходности 15%, период использования акции - 3 года, периодичность выплаты дивидендов - раз в году.

РV_акц = = 1178 руб.

Доход от акций состоит из суммы полученных дивидендов и дохода от прироста их стоимости. Текущая доходность определяется отношением суммы дивидендов по акции за последний год к курсовой стоимости акции:

Y_тек = × 100%.

Курсовая стоимость акции рассчитывается в сравнении с банковской депозитной ставкой (r_d):

Р_а = × 100%.

Конечная доходность акции (Y) - это отношение суммы совокупного дохода к первоначальной ее стоимости:

Y

---

Смотрите также файлы

• Устойчивость нелинейных систем. Особенности исследования устойчивости нелинейных сау.docx

• 1ВерноБаллов 1,00 из 1,00Отметить вопросТекст вопросаВ образовательных программах, ориентированных на достижение результатов определённого уровня, опыт самостоятельного .pdf

• Общее время решения 80 минут Теоретическая часть 1,4 балла за правильный ответ. Практическая часть, задачи 3,25 балла за правильный ответ.docx

• Тема 12. Кредитная политика Банка России. 12 Сущность и инструменты кредитной политики цб рф.docx

• Задача 1 Расчет лобовой врубки Рассчитать лобовую врубку, изображенную на рисунке, по исходным данным табл. 1.docx