Файл: Министерство науки и высшего образования рф федеральное государственное бюджетное учреждение высшего образования Российский государственный геологоразведочный университет имени Серго Орджоникидзе мгри.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.11.2023

Просмотров: 55

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



  1. На основании полученных результатов строим гистограммы:

Эмпирическая интегральная функция распределения





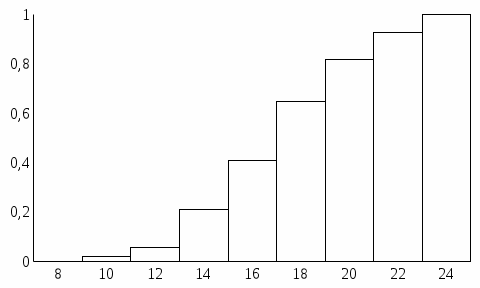
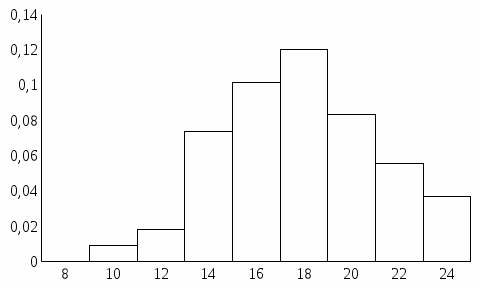
Эмпирическая дифференциальная функция распределения


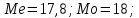
    1. Вычисление точечных оценок параметров распределения

Дана генеральная совокупность, из которой извлечена выборка объёмом N=54:

Класс А

Таблица А

11,28
10,69
11,18
8,2
10,6
9,73
8,71
9,96
8,21

12,02
8,27
7,17
7,88
7,27
8,66
8,59
6,82
6,46

7,82
10,81
9,82
10,7
10,25
7,73
12,23
11,04
9,12

9,4
12,53
7,26
8,77
5,98
10,39
8,77
8,97
6,84

7,17
8,07
3,99
10,25
8,39
11,56
9,69
5,6
12,41

8,97
10,33
8,26
6,23
10,57
11,81
9,73
5,25
10,85


Для этой выборки известны:

– середины интервалов группирования;

– частота попадания в интервал группирования.

Найдём

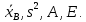
  1. Найдём выборочную среднюю:





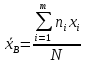
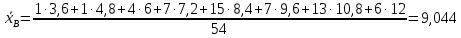
Заполним таблицу:










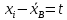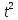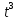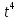3,6
-5,44
29,64
-161,38
878,65
1

4,8
-4,24
18,02
-76,46
324,55
1

6
-3,04
9,27
-28,22
85,91
4

7,2
-1,84
3,40
-6,27
11,57
7

8,4
-0,64
0,42
-0,27
0,17
15

9,6
0,56
0,31
0,17
0,10
7

10,8
1,76
3,08
5,41
9,50
13

12
2,96
8,74
25,82
76,31
6

  1. Вычислим квадрат стандарта:







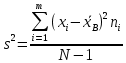
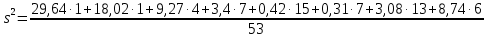
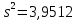
Стандарт равен:

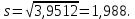
  1. Вычислим асимметрию:







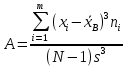
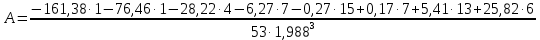
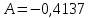
  1. Вычислим эксцесс:






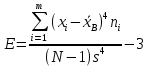
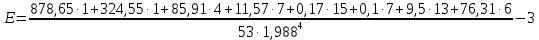
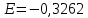
Класс Б

Таблица Б

12,3
14,06
12,38
11,96
10,78
12,8
8,82
9,24
13,07

12,39
10,23
12,57
10,43
11,95
11,03
10,23
8,23
14,46

11,28
13,21
10,72
10,87
12,04
12,2
8,32
11,04
11,94

11,53
12,34
10,23
11,76
10,02
11,21
16,45
9,64
6,33

12,64
10,3
11,52
8,8
6,62
12,25
11,77
12,41
8,65

8,19
9,73
13,37
8,49
14,35
8,31
10,69
9,44
11,42


Для этой выборки известны:

– середины интервалов группирования;

– частота попадания в интервал группирования.

Найдём

  1. Найдём выборочную среднюю:





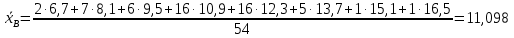
Заполним таблицу:














6,7
-4,37
19,14
-83,72
366,27
2

8,1
-2,97
8,85
-26,32
78,30
7

9,5
-1,57
2,48
-3,90
6,15
6

10,9
-0,17
0,03
-0,01
0
16

12,3
1,20
1,45
1,74
2,09
16

13,7
2,63
6,89
18,09
47,50
5

15,1
4,03
16,20
65,22
262,54
1

16,5
5,43
29,43
159,69
866,35
1

  1. Вычислим квадрат стандарта:







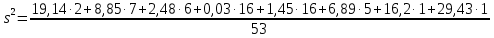
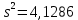
Стандарт равен:

Смотрите также файлы