Файл: 1 Кодирование текстовых и символьных данных.doc

1.11. Измерение и представление информации

Любая классификация всегда относительна. Один и тот же объект может быть классифицирован по разным признакам или критериям. Часто в зависимости от условий внешней среды объект может быть отнесен к разным классификационным группировкам. В основу классификации информации, циркулирующей между объектами, положены пять наиболее общих признаков:

• 
  место возникновения информации;
  
• 
  стадия ее обработки;
  
• 
  способ отображения информации;
  
• 
  стабильность информации;
  
• 
  функция управления информацией.
  

По первому признаку информацию можно разделить на входную, выходную, внутреннюю и внешнюю. Входная информация — это информация, поступающая на вход какого-нибудь устройства или объекта. Выходная информация — это информация на выходе объекта, предназначенная для передачи другому объекту. Одна и та же информация может быть входной для одного объекта и выходной для другого. Внутренняя информация возникает внутри объекта, внешняя за его пределами.

По второму признаку информация разделяется на первичную, вторичную, промежуточную и результатную. Первичная информация возникает непосредственно в процессе деятельности объекта и регистрируется на начальной стадии. Вторичная получается в результате обработки первичной информации, промежуточная используется в качестве исходных данных для последующих расчетов, результатная применяется для выработки управленческих решений.

По способу отображения информация подразделяется на текстовую и графическую. Текстовая информация — это совокупность алфавитных, цифровых и специальных символов, графическая — это различного рода графики, диаграммы, схемы, рисунки.

По стабильности информация может быть переменной (текущей) и постоянной. Постоянная информация подразделяется на справочную, нормативную и плановую.

Наконец, по функциям управления обычно классифицируют информацию экономического типа. При этом информация подразделяется на плановую, нормативно-справочную и оперативную (текущую). Плановая информация — это информация о параметрах объекта на будущий период, нормативно-справочная содержит различные нормативные и справочные данные, оперативная характеризует текущий момент.

---

Определить понятие "количество информации" довольно сложно. При анализе информации социального плана на первое место выходят такие ее свойства, как истинность, своевременность, ценность, полнота и т. п. Обращение к качественной стороне информации породило синтаксический, семантический и прагматический подход к ее оценке.

При синтаксическом подходе учитывают формально-структурные характеристики информации без рассмотрения ее смыслового содержания. Это тип носителя, способ представления информации, скорость передачи и обработки, размеры кодов и т. п. Все это — внешняя сторона структурных характеристик информации.

Семантический (смысловой) подход определяет степень соответствия образа объекта и самого объекта. Эта сторона учитывает смысловые связи, содержание информации, служит для формирования понятий и их обобщения.

Прагматический подход отражает отношение информации и ее потребителя, соответствие информации целям управления. Этот подход связан с ценностью и полезностью использования информации для принятия решений.

Все эти соображения, тем не менее, не противоречат важному результату теории информации о том, что в определенных, весьма широких условиях, можно, пренебрегая качественными особенностями информации, выразить ее количество числом, а следовательно, сравнивать количество информации, содержащейся в различных группах данных. Количеством информации называют числовую характеристику информации, отражающую ту степень неопределенности, которая исчезает после получения информации.

Исторически возникли два подхода к определению количества информации в синтаксическом смысле: вероятностный и "объемный". Вероятностный подход развил в конце 1940 гг. американский математик Шеннон¹, а “"объемный”" возник с изобретением ЭВМ. Понятия “"информация", "неопределенность", "возможность выбора" тесно связаны. Получаемая информация уменьшает число возможных вариантов выбора (т. е. неопределенность), а полная информация не оставляет вариантов вообще. "Объемный" подход самый простой. За единицу информации здесь принимается один бит. При этом невозможно нецелое число битов. Это количество информации, при котором неопределенность уменьшается вдвое, т. е. это ответ на вопрос, требующий односложного разрешения — да или нет. Однако бит слишком мелкая единица измерения информации. На практике чаще применяются более крупные единицы, например, байт и производные от него:

---

• 
  1 Килобайт (Кбайт) = 1024 ба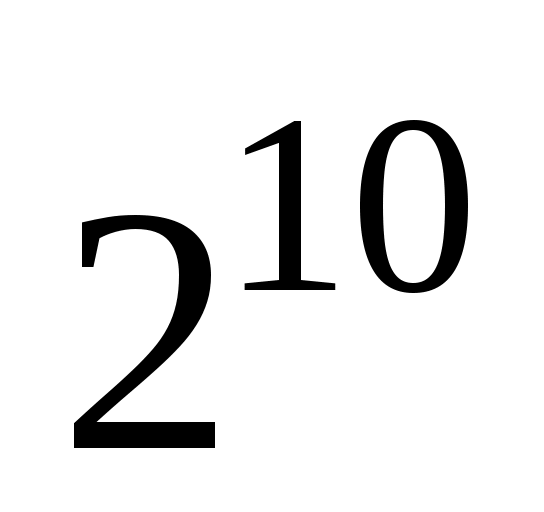йт = байт;
  
• 
  1 Мегабайт (Мбайт) = 1024 Кба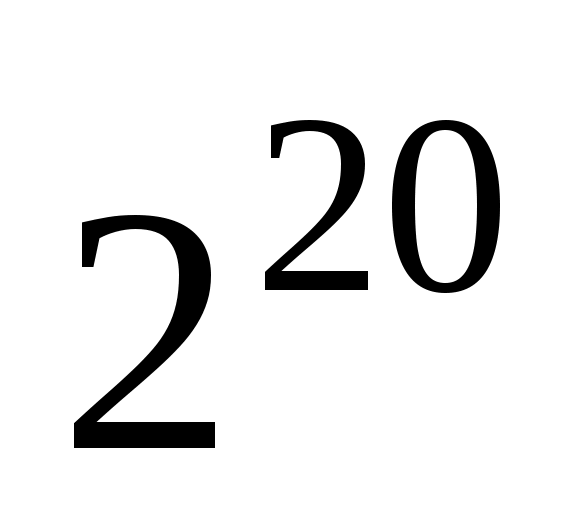йт = байт;
  
• 
  1 Гигабайт (Гбайт) = 1024 Мба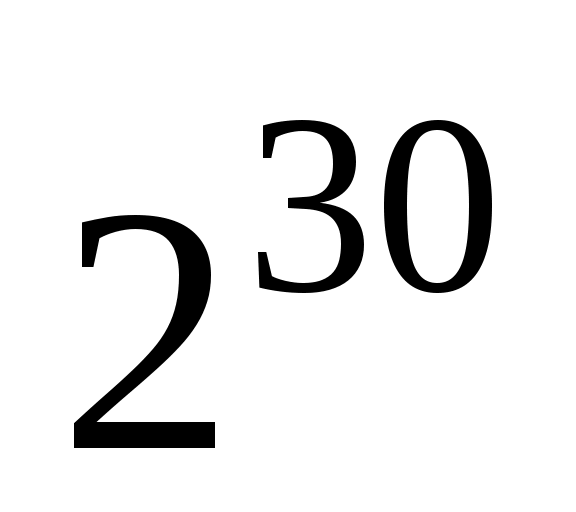йт = байт;
  
• 
  1 Терабайт (Тбайт) = 1024 Гб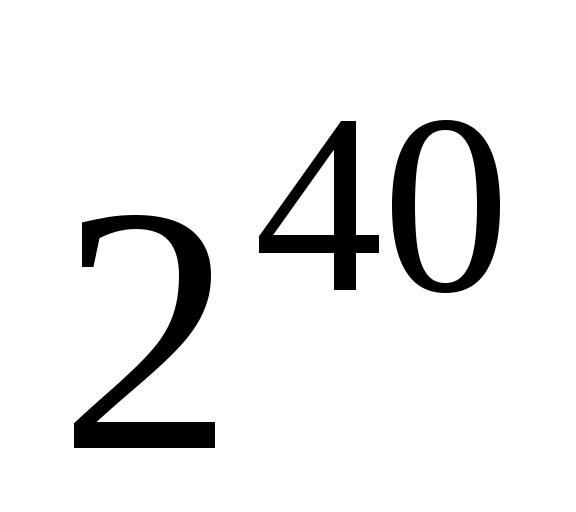айт = байт.
  

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации. Такая единица существует, но используется в компьютерной технике редко, что связано с аппаратными возможностями компьютеров.

При вероятностном подходе необходимо определить величину, измеряющую неопределенность — энтропию, которая обычно обозначается буквой . За количество информации, которое получено в ходе осуществления опыта принимается разность неопределенностей "до" и "после" опыта: . Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята , и, таким образом, количество полученной информации совпадает с первоначальной энтропией, т. е. неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта. Таким образом, количество информации об объекте обратно пропорционально энтропии объекта, а сама энтропия является мерой недостающей информации.

Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей граней. Величина и энтропия данного опыта

---

связаны между собой некоторой функциональной зависимостью . Определим вид этой функции. Если варьировать число граней и число бросаний кости , то общее число исходов опыта будет равно . Ситуацию с бросанием кости раз можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем — "однократных бросаний кости". Энтропия такой системы в раз больше, чем энтропия одной системы, т. е. . Но , отсюда . Подставим полученное значение в формулу для , тогда . Обозначая через положительную константу , т. к. , получим . Обычно принимают , таким образом получаем формулу Хартли²

(1.11.1)

Очевидно, что

---

будет равно единице, если , т. е. в качестве единицы информации принимается еёе количество, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов. Если рассматривать равновероятных исходов, то можно считать, что на долю каждого исхода приходиться одна -я часть общей неопределенности опыта , а вероятность -го исхода равна . Тогда

. (1.11.2)

Формула (1.11.2) называется формулой Шеннона.

Пример 1. Определим количество информации, связанное с появлением каждой буквы в сообщении: “"Жил-был у бабушки серенький козлик".

В этом сообщении 34 знака. Частоты и вероятности появлений букв в сообщении приведены в табл. 1.11.

По формуле Хартли имеем бит, аналогично по формуле Шеннона бит. Это значение меньше предыдущего. Величина , вычисленная по формуле (1.10.1), является максимальным количеством информации, приходящейся на один знак в сообщении.

Таблица 1.11. Частоты и вероятности букв в сообщении

Номер	Буква	Частота		Номер	Буква	Частота
1	ж	1	0.0294	11	к	4	0.1176
2	и	4	0.1176	12	с	1	0.0294
3	л	3	0.0883	13	е	2	0.0589
4	-	1	0.0294	14	р	1	0.0294
5	б	3	0.0883	15	н	1	0.0294
6	ы	1	0.0294	16	ь	1	0.0294
7	пробел	4	0.1176	17	й	1	0.0294
8	а	1	0.0294	18	о	1	0.0294
9	у	2	0.0589	19	з	1	0.0294
10	ш	1	0.0294

---