ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 123
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Изложенный подход хорошо применим при анализе технической информации. В информации социального плана на первый план выступают такие ее свойства, как истинность, своевременность, ценность, полнота и т. п. Обращение к качественной стороне информации породило иные подходы к ее оценке. При семантическом подходе информация рассматривается с точки зрения как формы, так и содержания. Для измерения смыслового содержания информации, т. е. ее количества на семантическом уровне наибольшее признание получила тезаурусная мера. Эта мера связывает семантические свойства информации со способностью пользователя принимать поступившие сообщения.
Р
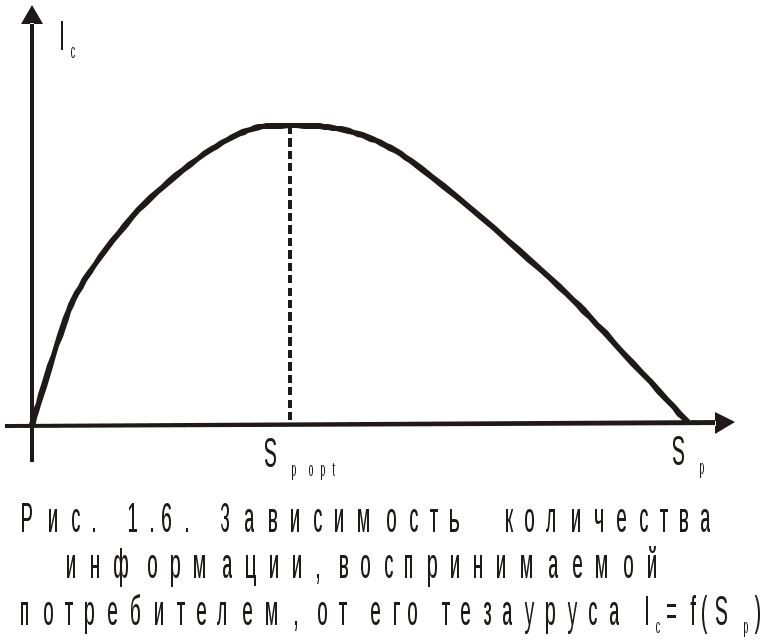
ис. 1.6. Зависимость количества информации, воспринимаемой потребителем, от его тезауруса
Тезаурусом называется словарь или свод данных, полностью охватывающий термины и понятия какой-нибудь специальной сферы, т. е. это совокупность сведений, которыми располагает объект. В зависимости от соотношений между смысловым содержанием информации
1.12. Теоремы Шеннона
При передаче сообщений по каналам связи всегда возникают помехи, приводящие к искажению принимаемых сигналов. Исключение помех при передаче сообщений является очень серьезной теоретической и практической задачей. Ее значимость только возрастает в связи с повсеместным внедрением компьютерных телекоммуникаций. Все естественные человеческие языки обладают большой избыточностью, что позволяет сообщениям, составленным из знаков таких языков, иметь заметную помехоустойчивость.
Избыточность могла бы быть использована и при передаче кодированных сообщений в технических системах. Самый простой способ повышение избыточности — передача текста сообщения несколько раз в одном сеансе связи. Однако большая избыточность приводит к большим временным затратам при передаче информации и требует большого объема памяти. К настоящему времени вопрос об эффективности кодирования изучен достаточно полно.
Пусть задан алфавит
Рассмотрим соответствие между буквами алфавита
. Алфавитное кодирование определяется следующим образом: каждому слову
При разработке различных систем кодирования данных получены теоретические результаты, позволяющие получить сообщение с минимальной длиной кодов. Два положения из теории эффективности кодирования известны как теоремы Шеннона.
Первая теорема говорит о существовании системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов (букв алфавита
Рассмотрим вновь пример 1 из раздела 1.11, закодировав анализированное сообщение по алгоритму Фано3. В таблице . 1.12 приведены коды букв в сообщении (слова
Таблица 1.12
-
Но-
мер
Бук-
ва
Код
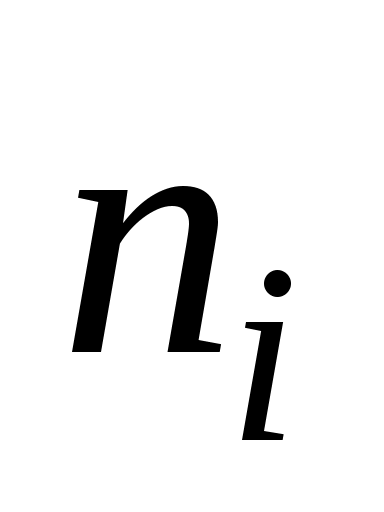

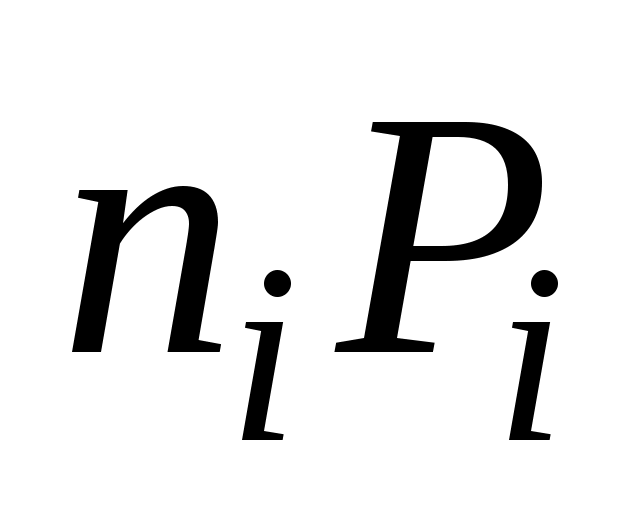
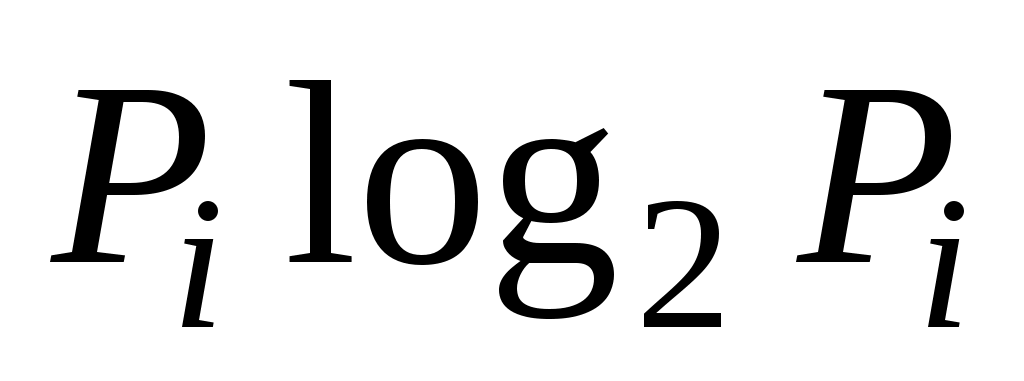
1
ж
10110
5
0.0294
0.1470
–0.1496
2
и
000
3
0.1176
0.3528
–0.3632
3
л
0111
4
0.0883
0.3532
–0.3092
4
-
10111
5
0.0294
0.1470
–0.1496
5
б
0110
4
0.0883
0.3532
–0.3092
6
ы
10101
5
0.0294
0.1470
–0.1496
7
пробел
001
3
0.1176
0.3528
–0.3632
8
а
10100
5
0.0294
0.1470
–0.1496
9
у
1000
4
0.0589
0.2356
–0.2406
10
ш
11000
5
0.0294
0.1470
–0.1496
11
к
010
3
0.1176
0.3528
–0.3632
12
с
11001
5
0.0294
0.1470
–0.1496
13
е
1001
4
0.0589
0.2356
–0.2406
14
р
11010
5
0.0294
0.1470
–0.1496
15
н
11011
5
0.0294
0.1470
–0.1496
Продолжение таблицы 1.12
-
Номер
Буква
Код




16
ь
11100
5
0.0294
0.1470
–0.1496
17
й
11101
5
0.0294
0.1470
–0.1496
18
о
11110
5
0.0294
0.1470
–0.1496
19
з
11111
5
0.0294
0.1470
–0.1496
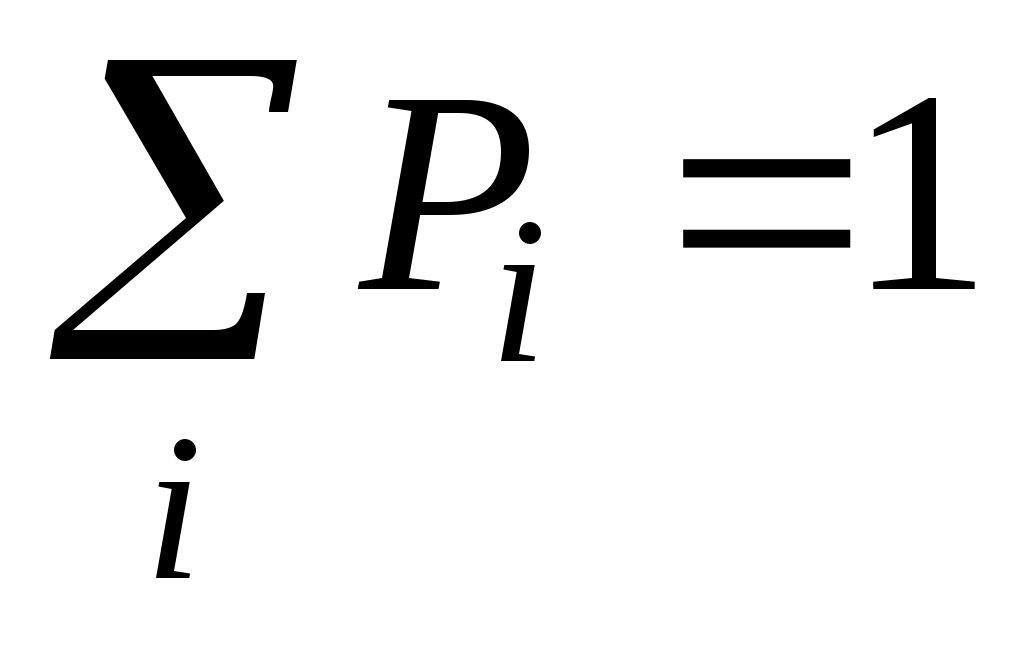
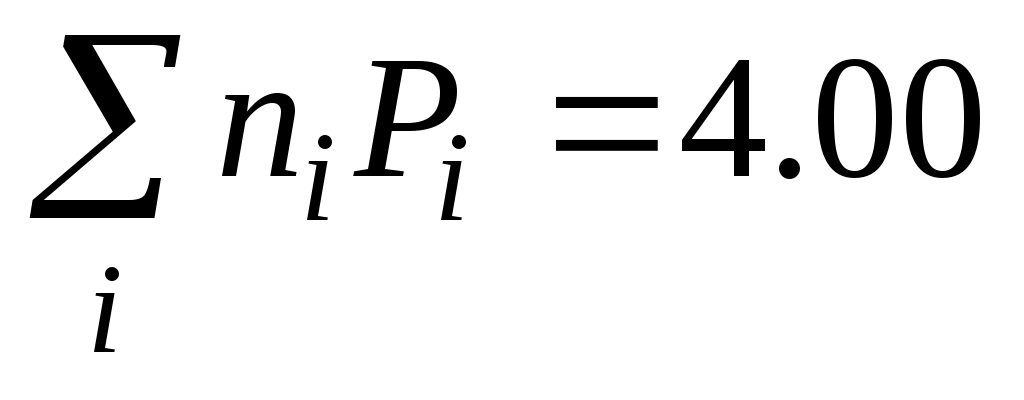
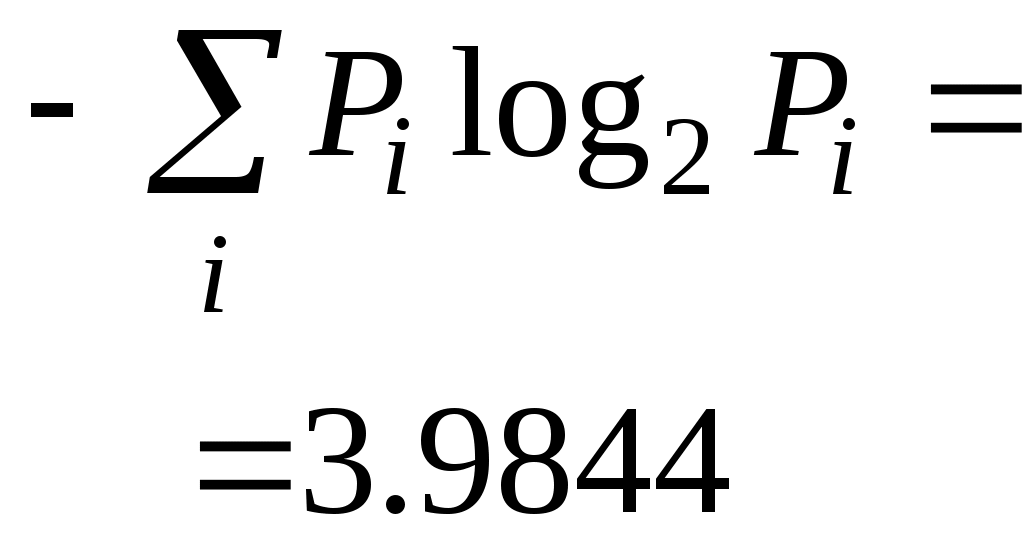
Математическое ожидание количества символов из алфавита